Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection
Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
670 Principles of Radiation Interaction in Matter and Detection
In dealing with intrinsic hadronic properties, we will consider calorimeter in
which cascades are fully contained. In fact, we have seen in Sect. 9.4.2 how lon-
gitudinal losses of electromagnetic visible-energy, amounting to a few percent, can
affect the calorimeter energy resolution. Later (Sect. 9.10.3), we will discuss similar
effects for hadronic calorimeters. From Eq. (3.78), it can be seen that about bet-
ween 4.5 and 5.6 λ
A
are needed in order to contain longitudinally 95% of hadronic
cascades for incoming hadrons with energy between 10 and 50 GeV. For instance,
the corresponding absorber thicknesses (see values of λ
A
in Table 3.4) are about
between 77 and 95 cm for iron or lead, and about between 48 and 60 cm for uranium,
respectively.
The large absorber depth needed is a main reason why homogeneous calorimeters
can hardly be employed in hadronic calorimetry at high energies. Homogeneous
(or quasi-homogeneous calorimeters, based on liquid argon [Cerri et al. (1989);
Fabjan (1995b)]) were developed (e.g., see [Hughes et al. (1969); Benvenuti et al.
(1975)]). However, the hadronic energy resolution of homogeneous calorimeters does
not improve below ≈ 10%, even at energies as high as 140 GeV [Benvenuti et al.
(1975)]. As it will be discussed in following sections, only in sampling calorimeters
the energy resolution can be improved up to values, where instrumental effects start
to dominate.
Hadronic calorimeters are usually sampling devices made of (as for electromag-
netic calorimeters, see Sect. 9.2) layers of passive samplers interleaved with active
readout planes.
The incoming particle energy is measured by means of the energy ²
vis
deposited
in the active layers with a thickness, usually, much smaller than the thickness of
the corresponding passive samplers.
Hadronic cascades are mostly generated in passive absorbers. Similarly to the
case of electromagnetic calorimeters, the sampling frequency, τ, is defined as the
passive sampler absorber thickness between two successive active planes, expressed
in units of interaction length (λ
A
). Only sampling calorimeters with constant τ
along the calorimeter depth will be considered in this book, unless explicitly stated
otherwise.
9.8.1.1 The e/h, e/π, h/mip and π/mip Ratios
While the energy (²
vis
) deposited in active layers mainly comes from processes of
energy loss by collisions, interactions leading to the generation of charged secondary
particles in electromagnetic and hadronic cascades (see Sects 2.4 and 3.3, respecti-
vely) are different. In particular, for hadronic showers, there is a large A-dependent
fraction of the incoming hadron energy spent in releasing nucleons and nucleon ag-
gregates (like α-particles), that are bound in atomic nuclei. As discussed by many
authors (see [Fabjan et al. (1977); Fabjan (1986); HELIOS Collab. (1987); Wig-
mans (1987); Br¨uckmann et al. (1988); Fesefelt (1988); Wigmans (1988); Brau and
Gabriel (1989); SICAPO Collab. (1989b,c, 1991b); Wigmans (1991, 2000); Byon-

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Principles of Particle Energy Determination 671
Wagner (1992); Beretvas et al. (1993); SICAPO Collab. (1993b); Gabriel et al.
(1994); SICAPO Collab. (1995a,b, 1996); Groom (2007)] and references therein),
this process has no equivalent in electromagnetic cascades and largely contributes
to the so-called hadronic invisible-energy. Therefore, at the same incoming energy,
we expect that the signal for electrons (or photons), e, differs (being usually larger)
from the signal for ideal hadrons, h.
These ideal hadrons are hadrons not accompanied by electromagnetic cascading
processes, i.e., for which f
em
≈ 0, where f
em
is the average fraction (see page
276) of incoming hadron energy deposited by electromagnetic cascades of secondary
particles and has been introduced in Sect. 3.3.1. We have:
e/h ≡
²
vis
(e)
²
vis
(h)
, (9.51)
where ²
vis
(e) and ²
vis
(h) are the visible energies, at the same incoming particle
energy, for electromagnetic and ideal-hadron showers, respectively. The e/h ratio is
usually larger than 1.
The process of nuclear interactions leading to hadronic shower multiplication
quickly degrades the incoming hadron energy. Thus, weakly energy dependent nu-
clear processes (see Sect. 3.3) occur (on average) at incoming secondary hadron
energies much lower than the incoming primary hadron energy. To a first appro-
ximation, we expect that, for an ideal hadron, the fraction of invisible energy is
independent of the incoming energy and is A-dependent. As in the case of electro-
magnetic showers for which ²
vis
(e) is proportional to E
e
[where E
e
is the incoming
electron, or photon energy, see Eq. (9.1)], we have that
²
vis
(h) ∝ E
h
, (9.52)
where E
h
is the incoming energy of an ideal hadron. Thus, the e/h ratio can be
considered as an intrinsic energy independent property of the calorimeter [HELIOS
Collab. (1987); Wigmans (1987); Br¨uckmann et al. (1988); Fesefelt (1988); Wigmans
(1988); Brau and Gabriel (1989); SICAPO Collab. (1989c); Acosta et al. (1991);
SICAPO Collab. (1991b); Wigmans (1991); Gabriel et al. (1994); SICAPO Collab.
(1995a,b, 1996)]. We expect that the e/h ratio may depend on the type and the
thickness of both the passive samplers and active layers.
The hadronic cascade of real hadrons is made of a pure electromagnetic compo-
nent and a pure hadronic component; the respective fractions of the total incoming
energy are f
em
and
f
h
= 1 − f
em
, (9.53)
respectively.
The visible energy ²
vis
(π), corresponding to a real hadron signal (π), can be
written in terms of pure electromagnetic and ideal hadronic signals (at the same
energy):
²
vis
(π) = f
em
²
vis
(e) + (1 − f
em
) ²
vis
(h). (9.54)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
672 Principles of Radiation Interaction in Matter and Detection
In Eq. (9.54), both ²
vis
(e) and ²
vis
(h) are expected to be proportional to the inco-
ming particle energy. However, the term f
em
has an approximate logarithmic energy
dependence [see Eq. (3.74)]. Then, in general, we expect that ²
vis
(π) is not linearly
dependent on the incoming hadron energy, contrary to what occurs for the visible
energy of electromagnetic showers, as experimentally observed ([Abramowicz et al.
(1981); HELIOS Collab. (1987); Wigmans (1988); Acosta et al. (1991); SICAPO
Collab. (1996)] and references therein).
From Eqs. (9.51, 9.54), the e/π signal ratio is:
e/π ≡
²
vis
(e)
²
vis
(π)
=
²
vis
(e)
f
em
²
vis
(e) + (1 − f
em
) ²
vis
(h)
=
[²
vis
(e)/²
vis
(h)]
f
em
[²
vis
(e)/²
vis
(h)] + (1 − f
em
)
=
e/h
1 − f
em
(1 − e/h)
. (9.55)
The e/π ratio contains the energy dependent term f
em
and, therefore, depends on
the energy of the incoming hadron. In addition, it depends on the atomic weight
of the absorber and on the Z-values of the passive samplers and active layers. This
latter Z-dependence is mostly caused by the electromagnetic shower component.
From Eq. (9.55), we can obtain the e/h ratio as a function of the e/π ratio, i.e.,
(e/π) [1 − f
em
(1 − e/h)] = e/h
⇒ (e/π) (1 − f
em
) = e/h [1 − f
em
(e/π)] ,
and, finally, we have:
e/h =
(e/π)(1 − f
em
)
1 − f
em
(e/π)
. (9.56)
The e/h ratio of a calorimeter can be evaluated experimentally by measuring the
e/π ratio at the same (and known) incoming energy for electrons and hadrons. For
instance, the e/h ratio of a lead / scintillating-fiber calorimeter was determined
by a set of experimental data taken from 5 up to 150 GeV [Acosta et al. (1990,
1991)]. The measured ratios of calorimeter responses to electrons and hadrons are
shown in Fig. 9.18 as a function of the incoming particle energy. The two curves
overimp osed represent the energy dependent e/π ratios obtained by using Eq. (9.55),
for f
em
= 0.11 ln[E(GeV)] [as given by Eq. (3.74)] and e/h = 1.15, and for f
em
=
[1 − E(GeV)
−0.15
] {e.g., see Eq. (3.75) and [Groom (1990)]} and e/h = 1.16.
In a hadronic sampling calorimeter, the visible energy is the result of collision
losses in the active readout layers by charged particles produced during the multi-
plication process. As was the case for electromagnetic calorimeters [see Sect. 9.2.2

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Principles of Particle Energy Determination 673
Fig. 9.18 The e/π ratio (adapted from Nucl. Instr. and Meth. in Phys. Res. A 308, Acosta,
D. et al., Electron, pion and multiparticle detection with a lead/scintillating-fiber calorime-
ter, 481–508, Copyright (1991), with permission from Elsevier, e.g., for the list of the authors
see [Acosta et al. (1991)]; see also [Leroy and Rancoita (2000)]) measured in a Lead/Scintillating-
fiber calorimeter. The continuous line corresponds to e/h = 1.15 and f
em
is calculated by means
of Eq. (3.74). The dashed line corresponds to e/h = 1.16 and f
em
= [1 − E(GeV)
−0.15
] {e.g., see
Eq. (3.75) and [Groom (1990)]}.
and Eq. (9.6)], the hadronic calorimeter response to minimum-ionizing and non-
showering particles
k
(mip’s), like muons, can be used as a scale or, equivalently, as
a unit of measurement of the response to hadronic showers.
The h/mip and π/mip ratios, for ideal and real hadrons, are defined by
h/mip ≡
²
vis
(h)
E
s
and π/mip ≡
²
vis
(π)
E
s
, (9.57)
where E
s
is the energy shared in the active readout planes following the partition
of a mip particle, given by Eq. (9.4). The value of ²
vis
(h) and E
s
are expected to b e
proportional to the incoming (ideal) hadron energy. As a consequence, the h/mip
ratio is an intrinsic energy independent property of the calorimeter, as is the e/h
ratio. The π/mip ratio depends on the hadron incoming energy [see Eq. (9.54)],
owing to the energy dependent term f
em
.
From Table 3.3, we see that the fraction of incoming energy lost through colli-
sions, mostly due to spallation protons, varies from ≈ 40% (high-A nuclei) to ≈ 60%
(low-A nuclei). In calorimeters, where neutrons contribute in a minimal way to the
k
One can see, for instance, [HELIOS Collab. (1987); Wigmans (1987); Br¨uckmann et al. (1988);
Wigmans (1988); SICAPO Collab. (1989b,c, 1990b, 1991b); Wigmans (1991); SICAPO Collab.
(1992a, 1993b); Gabriel et al. (1994); SICAPO Collab. (1995a,b, 1996)]

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
674 Principles of Radiation Interaction in Matter and Detection
overall visible-energy and the active media have a linear response to the energy
deposited by collisions, the h/mip ratio is expected to be slightly larger than ≈ 0.4
and ≈ 0.6 for high-A and low-A nuclei, resp ectively (see [Abramowicz et al. (1981);
HELIOS Collab. (1987); Br¨uckmann et al. (1988); Fesefelt (1988); SICAPO Collab.
(1989b,c, 1991b); Wigmans (1991); SICAPO Collab. (1993b); Gabriel et al. (1994);
Job et al. (1994); SICAPO Collab. (1995a,b, 1996)], and references therein). The
corresponding values of the e/mip ratios are about 0.50–0.65 and 0.70–0.85, respec-
tively (Sect. 9.2.2 and Table 9.1).
9.8.1.2 Compensating Condition e/h = e/π = 1 and Linear Response
In general, the calorimeter response to hadrons [²
vis
(π)] is intrinsically not propor-
tional to the incoming particle energy, as expressed by Eq. (9.54). This is mainly
caused by two combined effects (discussed in previous sections). The former is due
to the different fraction of energy deposited by ionization energy-loss in electro-
magnetic and pure hadronic components. The latter comes from the logarithmic
[e.g., see Eq. (3.74)] increase of the average fraction f
em
of the converted electro-
magnetic energy resulting from the photon decays of π
0
and η particles produced
during the hadronic cascade (Sect. 3.3.1).
From Eqs. (9.6, 9.54, 9.57), the overall visible-energy (electromagnetic and
purely hadronic) deposited by hadrons in the calorimeter can be written as:
²
vis
(π) = (π/mip)E
s
= E
s
[(e/mip)f
em
+ (h/mip)(1 − f
em
)]
= EF (S) {(h/mip) + [(e/mip) − (h/mip)] f
em
}
= EF (S) (h/mip) {1 + [(e/h) − 1] f
em
}, (9.58)
where (for mip’s) the energy shared E
s
and the fraction of energy lost F (S) are
given by Eq. (9.4); E is the incoming particle (hadron) energy. Equivalently, once
Eq. (9.7) is taken into account, Eq. (9.58) can be rewritten as:
²
vis
(π) = EF (S) (h/mip) {1 + [(e/h) − 1] f
em
}
e/mip
e/mip
= EF (S) (e/mip)
h
e
{1 + [(e/h) − 1] f
em
}
= ²
vis
(e) {(h/e) + [1 − (h/e)] f
em
}
= ²
vis
(e) {1 − f
h
[1 − (h/e)]}, (9.59)
where f
h
[Eq. (9.53)] is the fraction of energy deposited by the purely hadronic
shower component and ²
vis
(e) is the visible energy for an electron/photon of the
same energy of the hadron entering in the calorimeter.
When no absolute conversion energy scale is determined for measuring the de-
posited energy [²
vis
(π)], the calorimeter response to hadrons can be calibrated
by using electron b eams of known energies [Groom (1992); ATLAS Collab.
(1997)]. Thus, the calorimeter (linear) response to electrons is taken as equal to

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Principles of Particle Energy Determination 675
Fig. 9.19 Measured visible energies ²
vis
for the Si/Fe (◦) and the almost compensating Si/Pb+Fe
(dark squares) calorimeters (reprinted from Nucl. Instr. and Meth. in Phys. Res. A 368,
Furetta, C., Gambirasio, A., Lamarche, F., Leroy, C., Pensotti, S., Penzo, A., Rattaggi, M. and
Rancoita, P.G., Determination of intrinsic fluctuations and energy response of Si/Fe and Si/Fe
+ Pb calorimeters up to 70 GeV of incoming hadron energy, 378–384, Copyright (1996), with
permission from Elsevier; see also [Leroy and Rancoita (2000)]).
the incoming beam energy E
beam
and used as an energy scale for the calorimeter
response E
π
to hadrons of identical energy. The response to hadrons (scaled from
the electron response), which is sometimes called the mean visible hadron energy
(e.g., [Groom (1992); ATLAS Collab. (1997)]), can be written as:
E
π
= E
beam
[1 − (1 − f
em
)(1 − h/e)]
= E
beam
[1 − f
h
(1 − h/e)]. (9.60)
This equation follows from Eq. (9.59) once ²
vis
(e) is replaced by E
beam
and, as a
consequence, ²
vis
(π) by E
π
. Although E
π
is introduced in a way similar to ²
vis
(π), it
does not indicate a similar quantity, the former being a relative scaled energy, and
the latter an absolute measurement of the deposited energy in the active samplers. In
the following, when we need to make use of the scaled hadronic energy, we will refer
to it by explicitly indicating its notation E
π
.
In the previous section, we have seen that both e/h and h/mip ratios are energy
independent intrinsic properties of a sampling calorimeter. We must note [from
Eqs. (9.55, 9.56)] that if e/h = 1, we have e/π = 1 and vice-versa, i.e., the ratio e/π
becomes energy-independent. The condition e/h = e/π = 1 is called the compen-
sating condition or compensation condition (see [Wigmans (1987); Fesefelt (1988);
Wigmans (1988); SICAPO Collab. (1989b,c, 1991b); Wigmans (1991); SICAPO
Collab. (1993b); Job et al. (1994); SICAPO Collab. (1995a,b, 1996)] and references
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
676 Principles of Radiation Interaction in Matter and Detection
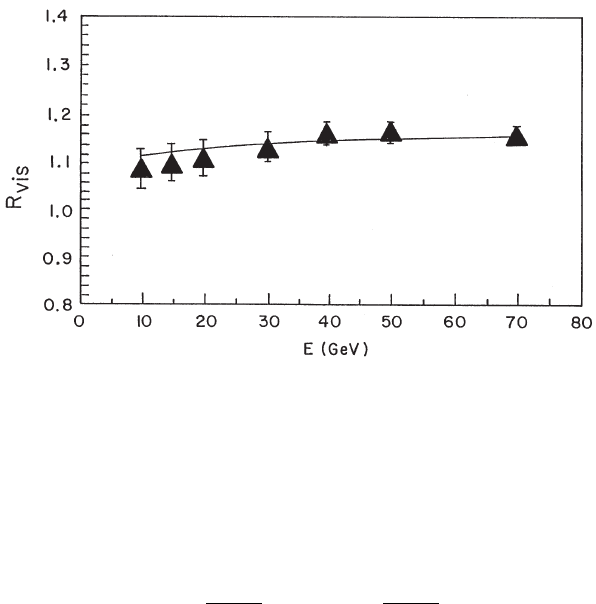
Fig. 9.20 Ratio R
vis
= ²
vis
(F e)/²
vis
(F e + P b) versus the incoming hadron energy (reprinted
from Nucl. Instr. and Meth. in Phys. Res. A 368, Furetta, C., Gambirasio, A., Lamarche, F.,
Leroy, C., Pensotti, S., Penzo, A., Rattaggi, M. and Rancoita, P.G., Determination of intrinsic
fluctuations and energy response of Si/Fe and Si/Fe + Pb calorimeters up to 70 GeV of incoming
hadron energy, 378–384, Copyright (1996), with permission from Elsevier; see also [Leroy and
Rancoita (2000)]).
therein). Furthermore from Eqs. (9.6, 9.57), and from Eqs. (9.51, 9.55), we have
e/h =
e/mip
h/mip
and e/π =
e/mip
π/mip
;
furthermore, when the compensating condition is satisfied, we have also that
h/mip = π/mip = e/mip
independently of the incoming particle energy. At very high energy, we obtain
e/π → 1, since f
em
→ 1
(see discussion on f
em
on page 276). As a consequence, at very high energies, the
calorimeter becomes almost compensating.
Equation (9.58) shows that it is only when e/mip = h/mip (i.e., for e/h = 1,
the compensation condition) that the calorimeter response is proportional to the
incoming hadron energy, E, independently of the energy dependent term f
em
. Thus,
we have
²
vis
(π) = (h/mip)E
s
= (h/mip) F (S) E, (9.61)
in a similar way to Eq. (9.7) for the electromagnetic cascades. It means that for a
hadronic calorimeter the most important requirement, i.e., its linear response, can
be fulfilled only under a very particular operating condition, namely the compen-
sation condition.
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Principles of Particle Energy Determination 677
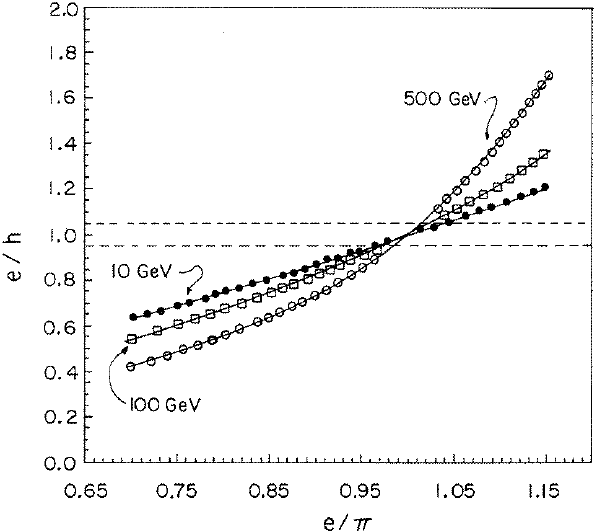
Fig. 9.21 e/h versus e/π [from Eqs. (3.74, 9.56)] at 10, 100, 500 GeV from [Leroy and Rancoita
(2000)]. The two dotted lines represent e/h = 0.95 and 1.05, respectively.
The restoration of the linear calorimeter response to the incoming hadron energy,
when the compensation condition is satisfied, was experimentally observed, see
e.g., [HELIOS Collab. (1987); SICAPO Collab. (1996)]. In Fig. 9.19, the mea-
sured visible hadroniv energies, ²
vis
, in MeV, for Si/Fe and Si/Fe+Pb sampling
calorimeters are shown as a function of the incoming hadron energy [SICAPO Col-
lab. (1996)]. The Si/Fe+Pb calorimeter is operated under an almost compensating
condition, i.e., e/h ≈ 1. The overimposed curve to the data (dark squares) is well
represented by a straight line crossing the origin of the axes. A slight deviation from
linearity, smaller than 3.5% over the full energy range, is observed for the experi-
mental data from the Si/Fe calorimeter (open circles), for which e/h ≈ 1.16. Fi-
gure 9.20 shows the ratio R
vis
= ²
vis
(F e)/²
vis
(F e + P b) versus the energy. The
overimp osed line is calculated using Eq. (9.54), with f
em
as given by Eq. (3.74),
and taking into account the e/h values of the two calorimeters [SICAPO Collab.
(1996)]. The R
vis
dependence on the incoming hadron energy is due to the non-linear
energy response of the Si/Fe calorimeter (≈ 3.5% over the entire energy range, as
mentioned above).
A linear energy response was also observed in compensating U/plastic-
scintillator calorimeters, like the one from [HELIOS Collab. (1987)] for hadrons
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
678 Principles of Radiation Interaction in Matter and Detection
of energy between 8 and 200 GeV.
The extent to which the lack of compensation affects the non-linear calorimeter
response to incoming-hadron energy depends on the e/h ratio. We can describe
the non-linear behavior, N
l
, of a hadronic calorimeter between the reference energy
of 10 GeV and any incoming-hadron energy E (in GeV), by considering its linear
response to electromagnetic cascades for which ²
vis
(e, E) = (E/10)²
vis
(e,10 GeV):
N
l
=
¯
¯
²
vis
(π, E)
¡
10
E
¢
− ²
vis
(π, 10 GeV)
¯
¯
²
vis
(π, 10 GeV)
=
¯
¯
¯
¯
²
vis
(π, E)
²
vis
(π, 10 GeV)
µ
10
E
¶
− 1
¯
¯
¯
¯
=
²
vis
(e, 10 GeV)
²
vis
(e, E)
µ
E
10
¶
¯
¯
¯
¯
²
vis
(π, E)
²
vis
(π, 10 GeV)
µ
10
E
¶
− 1
¯
¯
¯
¯
=
¯
¯
¯
¯
e/π(10 GeV)
e/π(E)
− 1
¯
¯
¯
¯
=
|e/π(10 GeV) − e/π(E)|
e/π(E)
, (9.62)
where the ratio e/π [see Eq. (9.55)] depends on the intrinsic ratio e/h and on the
energy dependent term f
em
. Thus, using Eq. (9.55), Eq. (9.62) can equivalently be
rewritten as
N
l
=
¯
¯
¯
¯
¯
·
e/h
1−f
em
(10 GeV)(1 − e/h)
−
e/h
1−f
em
(E)(1 − e/h)
¸·
e/h
1−f
em
(E)(1 − e/h)
¸
−1
¯
¯
¯
¯
¯
=
¯
¯
¯
¯
f
em
(10 GeV)(1 − e/h) − f
em
(E)(1 − e/h)
1−f
em
(10 GeV)(1 − e/h)
¯
¯
¯
¯
=
¯
¯
¯
¯
[f
em
(10 GeV) − f
em
(E)]
·
1 − e/h
1−f
em
(10 GeV)(1 − e/h)
¸
¯
¯
¯
¯
.
In Fig. 9.21, the curves, relating the two ratios e/h and e/π, are calculated
by means of Eqs. 3.74, (9.56), for e/h differing by 5% from the compensating va-
lue. From Fig. 9.21 we can estimate that N
l
[see Eq. (9.62)] is ≈ 2% at 500 GeV. N
l
is ≈ 6.7% (3.7%) at 500 GeV (100 GeV), for e/h ≈ 1.15.
9.9 Methods to Achieve the Compensation Condition
The e/π signal ratio is determined by processes that occur at the nuclear and
atomic levels during the cascade development. A large amount of the deposited
energy in a hadron calorimeter goes into breaking nuclei (binding energy) or into
low-energy neutrons and, therefore, is partially not visible. In addition, charged π
and µ decays produce secondary particles like ν, which are undetected. As discussed
in Sect. 3.3, the nuclear effects, which dominate pure hadronic cascades, have no
counterpart in electromagnetic cascades. Therefore, the calorimeter response to the
electromagnetic and non-electromagnetic part of the hadronic cascade is different,

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Principles of Particle Energy Determination 679
with the consequence that, in general, the electromagnetic (e) to hadronic (π) signal
ratio e/π 6= 1.
The energy independent equalization between the electromagnetic and the
hadronic signals (e/π = 1, i.e., the compensation condition, see page 675) is the
condition to restore the linear response of the calorimeter to hadronic cascades,
and, as will be discussed in the next section, to obtain an energy resolution that
improves as 1/
√
E, where E is the incoming hadron energy.
Calorimeter compensation physics, see e.g., [Wigmans (1987); Br¨uckmann et
al. (1988)], deals with the flux, the deposition and the fluctuation of the energy
coming from the cascade process. The energy deposition in both passive and ac-
tive samplers mainly occurs via collision losses of i) relativistic hadrons produced
in the interactions on target nuclei, ii) quasi-direct spallation protons coming from
the target nuclei and iii) electrons and positrons generated by the electromagnetic
component of the hadronic cascade. Additionally, prompt gamma radiation may
be emitted from excited fission products, or after particle evaporation from resi-
dual nuclei. Moreover, sources of delayed gamma photons are neutron capture pro-
cesses, when they occur. These photons can subsequently interact via the Compton
or the photoelectric effects and, in turn, generate a fast electron. Neutrons may
transfer part of their energy in neutron–nucleus collisions, particularly on low-A
nuclei. Furthermore, since most of the protons contributing to the hadronic signal
are highly non-relativistic, the saturation properties of the detecting medium for
densely ionizing particles (for instance, the scintillator light output) are of crucial
importance. This effect was intensively investigated, when the first compensation
calorimeters were operated (e.g., see [Brau and Gabriel (1985); HELIOS Collab.
(1987); Wigmans (1987); Br¨uckmann et al. (1988); Brau, Gabriel and Rancoita
(1989)] and references therein).
Various approaches to the realization of the compensation condition exist. One
method mainly depends on the quantity of hydrogen contained in the active
medium, and on the A-value of the passive samplers. The increase of the hadronic
signal, i.e., of the h/mip ratio, can be obtained by detecting part of the energy car-
ried by neutrons, which are generated in the cascade process. In fact, when hydrogen
rich materials (for instance plastic scintillators or scintillating fibers) are employed
as active media, neutron–proton scattering processes generate fast recoiling and
ionizing protons in active samplers (see, e.g., [Fabjan et al. (1977); Abramowicz et
al. (1981); De Vincenzi et al. (1986); Bernardi et al. (1987); HELIOS Collab. (1987);
Drews et al. (1990); Ros (1991)]).
The e/mip ratio can also be tuned by an appropriate choice of both passive
samplers and active media (see Sects. 9.2 and 9.3 and, e.g., [SICAPO Collab. (1990a,
1991b); Byon-Wagner (1992); SICAPO Collab. (1992a); Beretvas et al. (1993)] and
references therein).
In the following, we will call almost compensating calorimeter a calorimeter for
which the measured e/π ratio is ≈ between 0.95 and 1.05, within ≈ 5% experimental
