Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

690 Principles of Radiation Interaction in Matter and Detection

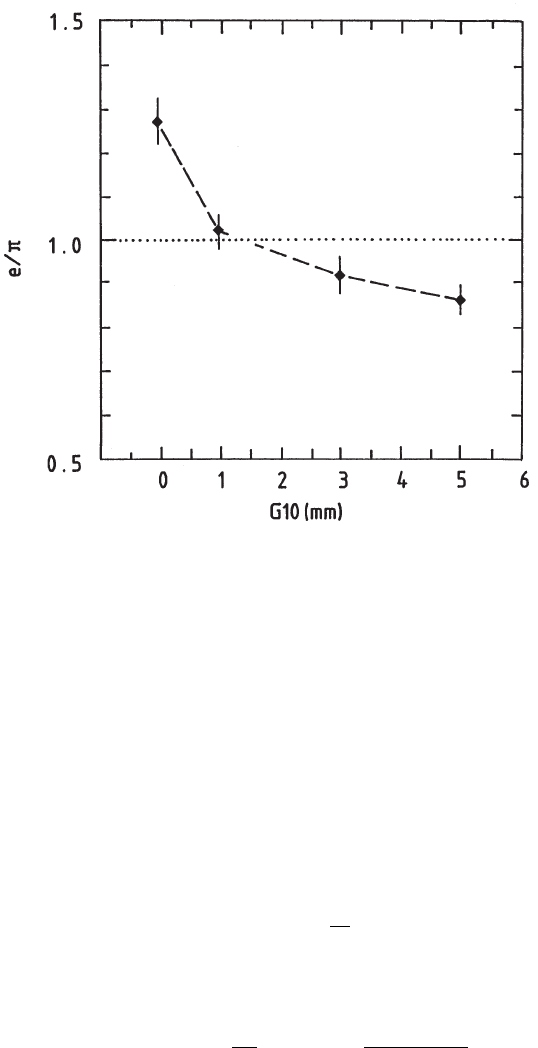
Fig. 9.25 Measured values of the e/π ratio for a Si/U calorimeter (see text) versus the thickness

of additional G10 plates (reprinted from Phys. Lett. B 242, Angelis, A.L.S. et al., Evidence for

the compensation condition in Si/U hadronic calorimetry by the local hardening eﬀect, 293–298,

Collab. (1990a)]; see also [Leroy and Rancoita (2000); SICAPO Collab. (1991b)]). The line is to

guide the eye.

The local hardening eﬀect was achieved and studied for low-Z materials such

as G10, Al and polyethylene. The reduction of the electromagnetic visible-energy

depends, to some extent, on the thickness and type of the readout layers. In fact, for

typical detector thicknesses of 400 µm silicon, 2.5 mm scintillator and 2 mm liquid

argon, mip’s (which can be considered as scale units for energy deposition of fast

particles) deposit ≈ 140, 500, and 440 keV, respectively, while the low-Z absorbers

(for the local hardening eﬀect) act mainly on soft electrons, generated in regions of

the high-Z passive samplers very close to surfaces adjacent to the active readout

media. This generated visible-energy reduction,

∆²

(low−Z), is almost independent

of the sampling fraction (Sect. 9.2.3), i.e., of the thickness of the high-Z passive

absorber.

From Eq. (9.66), we introduce the fraction R

(low−Z) deﬁned as:

(low−Z) = 1 −

∆²

(low−Z) =

vis

(low−Z)

vis

. (9.69)

(low−Z) is independent of the thickness of the passive sampler, but depends on

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Principles of Particle Energy Determination 691

the thickness (and the location, i.e., in front or at the rear, see Sect. 9.2.3) of the

low-Z material added for achieving the local hardening eﬀect.

Let us consider incoming electrons and protons on calorimeters which have diﬀe-

rent high-Z thicknesses U and U

, respectively. The ratio of the two e/π calorimeter

ratios can be written as:

R(e/π) ≡

e/π(U, low−Z)

e/π(U

, low−Z)

vis

(e, U, G10)

vis

(e, U

, G10)

vis

(π, U

, G10)

vis

(π, U, G10)

. (9.70)

From Eqs. (9.6, 9.69), the electromagnetic visible-energy becomes:

vis

(e, U, G10) = ²

vis

(e, U) R

(G10) = R

(G10) (e/mip) E

(U), (9.71)

where R

(G10) is almost independent of the sampling frequency (i.e., independent

of the thickness of the high-Z passive sampler) and, as discussed in Sect. 9.2.2,

e/mip becomes independent of the sampling frequency, τ , for values of τ larger

than ≈ 0.8. Thus we have:

vis

(e, U, G10)

vis

(e, U

, G10)

(U)

)

This way, the ratio R( e/π) of Eq. (9.70) can be written as:

R(e/π) '

(U)

)

vis

(π, U

, G10)

vis

(π, U, G10)

. (9.72)

Figure 9.26 shows the ratio R(e/π) for silicon calorimeters with U sampler

2.5 cm (data from [SICAPO Collab. (1995a)]) and 1.5 cm thick (data from [SICAPO

Collab. (1990a)]) as function of the added G10 plate thickness. The ratio

(2.5 cm U)/E

(1.5 cm U) was calculated by means of Eq. (9.4). The ratios

vis

(π, 1.5 cm U, G10)/²

vis

(π, 2.5 cm U, G10) were evaluated from an average (over

the incoming hadron energies of 8, 10, and 12 GeV) of the measured visible ener-

gies in the two experiments mentioned above. Experimental data indicate that the

R(e/π) ratio is quite consistent with 1, namely the e/π ratio does not depend on

the thickness of the uranium passive samplers, but on the thickness of the added

low-Z absorbers.

Once the compensating condition or an almost compensating condition (as a

result of the local hardening eﬀect) is achieved in calorimeters marginally sensitive

to the energy carried by neutrons, it becomes possible to vary the calorimeter sam-

pling frequency, while keeping the e/h ratio almost consistent with 1. Thus unlike

the case of active detectors with hydrogeneous materials, we can operate compen-

sating calorimeters in which the ratio of the thicknesses of passive samplers to active

readout media is variable. In this way, it is possible to vary the contribution of sam-

pling ﬂuctuations to the overall calorimeter energy resolution (see next section) by

modifying the sampling frequency, but keeping the compensation condition.

The achievement of the compensation condition, in the case of an absorber made

of Pb and Fe, results from the exploitation of the ﬁltering eﬀect. This was demon-

strated and systematically studied by an experiment performed by the SICAPO

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

692 Principles of Radiation Interaction in Matter and Detection

Collaboration [SICAPO Collab. (1992a, 1993a)], using silicon detectors as readout

medium. The sampling hadron calorimeter consisted of sets of absorbers made of Fe

or Fe and Pb plates, interspaced with silicon readout mosaics. In each sampling, the

thickness of Pb and Fe, as well as the respective positions of the absorbers plates,

are kept constant. Each set of absorbers is 23 mm thick. The mosaic supporting

structure is equivalent to ≈ 2.5 mm thick Fe absorber and this thickness has to

be added to the overall thickness of the sampling absorbers. The incoming particle

energies are 6, 8, 10, and 12 GeV. The energy deposited by the incoming electrons

and pions was measured for the F-conﬁguration FePb–Si–FePb [²

vis

(F)] and for the

R-conﬁguration PbFe–Si–PbFe [²

vis

(R)], where a reduction of the visible energy is

expected, as a consequence of the ﬁltering eﬀect [SICAPO Collab. (1993a,c)] (see

Sect. 9.3). In both conﬁgurations, the thickness of Pb was varied from 3 mm to

13 mm. The thickness of Pb was kept constant inside each sampling in each conﬁ-

guration. Data were also taken with Fe as the only absorbers for comparison.

Let us deﬁne the ratio

vis

(F)

vis

(R)

For incoming electrons, we have that the value of R

corresponds to the ratio of

the e/mip values for the F- and R-conﬁgurations [see Eq. (9.15) and Sect. 9.3.1],

because the shared energy, E

, does not depend on the sequence of absorbers [see

Eqs. (9.4, 9.5)]:

(e) =

vis

(e, F)

vis

(e, R)

e/mip(F)

e/mip(R)

. (9.73)

(e) was found to increase almost linearly (Fig. 9.11) as a function of the Pb

thickness, above a few mm of Pb absorber, when the ﬁltering eﬀect is acting.

For hadronic cascades we have to remember that the ﬁltering eﬀect acts on the

electromagnetic component of the hadronic shower, and that ²

vis

(h, F) ≈ ²

vis

(h, R)

and E

(F) = E

(R), since there is no change of the thickness of samplers (passive

and active) in the two conﬁgurations, but only an interchange of the passive sam-

pler lo cations. As a consequence, h/mip values are unaﬀected. The second term of

Eq. (9.67) can be neglected, when the equation expresses the visible-energy reduc-

tion for the case of the ﬁltering eﬀect; namely the visible-energy reduction between

the F- and the R-conﬁguration is expressed by Eq. (9.68). This equation can be

rewritten as a function of electromagnetic visible energies as:

∆²

(π, FR) ≡

vis

(π, R) − ²

vis

(π, F)

vis

(π, R)

1 −

vis

(π, F)

vis

(π, R)

= 1 − R

(π) ≈ e/π(R) f

∆²

(e, FR)

= e/π(R) f

1 −

vis

(e, F)

vis

(e, R)

= e/π(R) f

[1 − R

(e)], (9.74)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Principles of Particle Energy Determination 693

where

(π) =

vis

(π, F)

vis

(π, R)

and e/π(R) is the e/π ratio of the R-conﬁguration; ﬁnally, we have:

(π) ≈ 1 − e/π(R) f

[1 − R

(e)]. (9.75)

The mean energy deposited in the calorimeter ²

vis

(e) (found to be linear as a

function of the incident energy, e.g., see Figs. 9.9 and 9.10) decreases with the thick-

ness of Pb in the absorber. Using identical passive absorber thicknesses, the values

of the visible-energy, measured with the PbFe–Si–PbFe R-conﬁguration [²

vis

(R)],

are lower than those measured with the FePb–Si–FePb F-conﬁguration [²

vis

(F)] for

incoming both electrons and pions, as expected because of the ﬁltering eﬀect.

For instance, the ratio R

(e) for incoming electrons is 1.23 ± 0.05 for a Pb

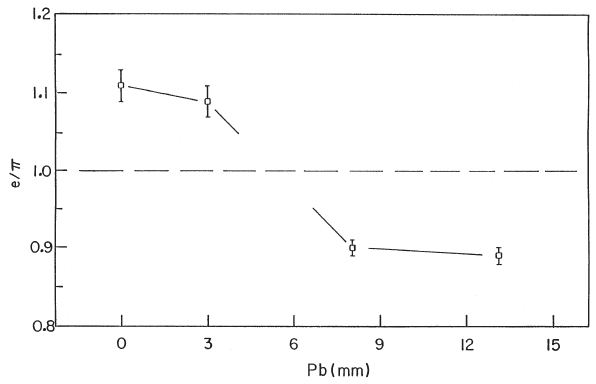
thickness of 13 mm. The e/π(R) ratio (Fig. 9.27), measured for the PbFe–Si–PbFe

conﬁguration with 13 mm of Pb plates, is 0.89 ± 0.01 [SICAPO Collab. (1992a,

Fig. 9.26 The ratio R(e/π) (reprinted from Nucl. Instr. and Meth. in Phys. Res. A 361,

Furetta, C., Leroy, C., Pensotti, S., Penzo, A. and Rancoita, P.G., Experimental determination

of the intrinsic ﬂuctuations from binding energy losses in Si/U hadron calorimeters, 149–156,

sampler 2.5 cm (data from [SICAPO Collab. (1990a)]) and 1.5 cm (data from [SICAPO Collab.

(1995a)]]) thick versus the added G10 plates thickness (on the front and on the rear the silicon

mosaics). The silicon mosaics had supporting structure made by two G10 sheets of 0.2 and 1 mm

thick, respectively. The line represents R(e/π) = 1.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

694 Principles of Radiation Interaction in Matter and Detection

1993a)]. Furthermore, for instance at 6 [12] GeV, the expected average fraction of

the converted electromagnetic energy in a pion cascade is f

≈ (20–22)% [(27–

30)%], with an average value among 6, 8, 10 and 12 GeV of ≈ (24–26)%. Using

Eq. (9.75), and measured e/π(R), R

(e) and calculated f

ratios, the estimated

value of R

(π) for incoming pions becomes:

(π) ≈ 1 − 0.89 × 0.25 × (1 − 1.23) ≈ 1.05.

This latter value is quite consistent within with the measured ratio:

FR,measured

(π) = 1.06 ± 0.03.

The diﬀerent rate of reduction of the visible energy for electrons and pions al-

lows to tune the e/π ratio and, therefore, to achieve the compensation condition in

a Si/Pb+Fe hadron calorimeter. A fundamental characteristic of the ﬁltering eﬀect,

in PbFe–Si–PbFe calorimeters, is the linear decrease of the e/mip ratio as the Pb

fraction, f [Eq. (9.14)], increases (Sect. 9.3). This dependence on f was experimen-

tally observed [SICAPO Collab. (1989c)] for the entire f -range investigated, namely

for f values between ≈ (5–36)%.

The e/π values for the PbFe–Si–PbFe R-conﬁguration (from an average of mea-

surements performed at incoming particle energies of 6, 8, 10, and 12 GeV) are

shown in Fig. 9.27 (from [SICAPO Collab. (1992a)]) as a function of the thickness

of Pb in the Pb+Fe absorber. It is observed that the e/π ratio decreases from the

value 1.11 ± 0.02, when Fe is the only Fe absorber, to the value 0.89 ± 0.01 for a

Pb thickness of 13 mm. From these experimental data, the thickness of Pb to be

inserted in the absorber in order to achieve the compensation condition (e/π = 1)

is estimated to be (5.4 ± 1.0) mm. The Pb thickness of (5.4 ± 1.0) mm corresp onds

to a fraction f of Pb present in the absorber of about (22–24)% (in calculating this

fraction, the thickness of Fe takes into account the amount of material serving as

support of the silicon mosaics). This experimental result is in agreement with the

prediction, based on Monte-Carlo simulations, for which the compensation has to

be achieved for f ≈ 25% in a PbFe–Si–PbFe calorimeter with Fe absorber thickness

of about 35 mm [SICAPO Collab. (1989c)] (see also [Brau and Gabriel (1989)]).

Other quasi compensating calorimeters using values of f between ≈ (20–25)%

were operated [SICAPO Collab. (1995b, 1996)]. Among these compensating (or

almost compensating) calorimeters, the minimal thickness of Fe absorber sampler

used is ≈ 15 mm (i.e., ≈ 0.85 X

). In general, the ratios of the thicknesses of Pb

absorbers to Fe absorbers (for which the compensation condition was achieved) are

≈ 0.94, when the ratio is calculated in units of radiation lengths, and ≈ 0.29, when

the ratio is calculated in units of interaction lengths.

Once the appropriate value of f is maintained (as well as the conﬁguration) for

keeping the compensation, the overall passive sampler thickness can be readjusted,

i.e., the thicknesses of passive samplers can be varied to modify the sampling ﬂuc-

tuations contribution to the overall hadronic energy resolution (see next section).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Principles of Particle Energy Determination 695

The ﬁltering eﬀect can also act, when other low-Z and high-Z materials are

combined as passive samplers (Sect. 9.3). The value of f, required to achieve the

compensation condition, depends on the h/mip ratio of the calorimetric structure. In

fact, this value is related to the calorimeter response to the purely hadronic energy,

i.e., also to the type of active detectors. As a consequence, the ratio (of ≈ 1) between

the radiation lengths of Fe and Pb absorbers needs to be optimized, when replacing

silicon readout with other active detectors.

The e/π ratios measured in the FePb–Si–FePb F-conﬁguration (see [SICAPO

Collab. (1993a,c)]) never achieved values close to compensation, except when the

Pb thickness inserted in the absorber represents a fraction (f ) larger than 50%. The

decrease of the e/π ratio value, in the case of the FePb–Si–FePb F-conﬁguration,

is expected because the e/π ratio value for the Pb absorber is lower than the one

for the Fe absorber. Thus, as the Pb fraction increases the overall e/π value has to

decrease slightly. However, the compensation condition is not reached without a fur-

ther reduction of the calorimeter response to the electromagnetic component. This

reduction is achievable by exploiting the propagation properties of the electromag-

netic shower in complex absorbers (as discussed above and in Sect. 9.3).

These exp erimental results were reproduced by simulations [Giani (1993)] using

the GEANT program code [Brun et al. (1992)] and the FLUKA package [Aarnio

Fig. 9.27 The e/π ratio for PbFe–Si–PbFe R-conﬁguration as a function of the thickness of

Pb absorber in the passive sampler (the overall thickness, including the Fe plate, of the passive

sampler is 23 mm). The data are from an average at incoming particle energies of 6, 8,10, and

12 GeV (reprinted from Phys. Lett. B 280, Borchi, E. et al., Evidence for comp ensation in a

Si/(Fe, Pb) hadron calorimeter by the ﬁltering eﬀect, 169–174, Copyright (1992), with permission

from Elsevier, e.g. for the list of the authors see [SICAPO Collab. (1992a)]; see also [Leroy and

Rancoita (2000)]). The line is to guide the eye.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

696 Principles of Radiation Interaction in Matter and Detection

et al. (1987)] for the hadronic interactions (see also [Hirayama (1992)]). These si-

mulations, using the geometry and the exact composition of the sampling material

(at the 1% level) of the experimental setup, have yielded results which are in go od

agreement with the measured e/π ratio values for both conﬁgurations [SICAPO

Collab. (1993a)]. The simulations indicate that the precise knowledge of the com-

position of the supporting structure is a very important element for determining

the agreement between experimental and Monte-Carlo data.

The local hardening and ﬁltering eﬀects can be combined. Soft electrons survived

to the ﬁltering eﬀect in Pb-Fe samplers can be absorbed by additional thin (in units

of radiation lengths) low-Z plates inserted in the calorimeter conﬁguration next to

the active detectors.

As already discussed (e.g., see Sect. 9.2.3), the local hardening eﬀect modi-

ﬁes the e/mip ratio, also when other active media, like plastic scintillators, are

employed. The maximum achievable e/mip ratio reduction was estimated [Wig-

mans (1988)] to be ≈ 8% by EGS4 Monte-Carlo calculations. For instance, the

Reconﬁgurable-Stack calorimeter (see [Byon-Wagner (1992); Beretvas et al. (1993);

Job et al. (1994)], and references therein) used plastic scintillators as readout media

and a combination of Pb (3.2 mm thick) and Fe (25.4 mm thick) absorbers as passive

samplers, with a value f ≈ 11%. The plastic scintillators were cladded with 1.6 mm

Al plates, in order to vary the mip ratio by exploiting the local hardening eﬀect. The

measurements [Job et al. (1994)] using F- and R-conﬁguration have shown that the

e/π ratio at 10 GeV was decreased by ≈ 0.17 (with respect to the one measured with

the F-conﬁguration), reaching the value of 1.10 ± 0.03 with the R-conﬁguration.

9.10 Compensation and Hadronic Energy Resolution

The particle multiplication in calorimeters is based on statistical processes (although

due to diﬀerent types of interactions in matter) for both electromagnetic, already

discussed in Sect. 9.4.1, and hadronic cascades. In sampling devices the hadronic

visible-energy depends (Sects. 9.8, 9.9) on the number of secondary ionizing parti-

cles and on particles (like fast neutrons) able to produce ionizing recoil protons in

hydrogeneous active media or ionizing recoil nuclei in any other detectors. Statisti-

cal ﬂuctuations (e.g., see [Amaldi (1981); Fabjan (1985a, 1986)]) of the number of

created and recoil particles cause ﬂuctuations of the visible-energy deposited in the

readout detectors and, consequently, limit the obtainable energy resolution which,

for an incoming hadron with energy E, is given by

σ(E)

≡

σ(²

vis

)

vis

(π)

, (9.76)

where σ(²

vis

) is the standard deviation of the distribution of the hadronic visible-

energy ²

vis

(π).

Because of the statistical nature of the cascade phenomenon, the energy reso-

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Principles of Particle Energy Determination 697

lution is expected to improve, that is σ(E)/E decreases, with the increase of the

energy. In electromagnetic sampling calorimetry (Sect. 9.4), we have seen that the

linear relationship between the incoming energy and the visible energy determines

both the 1/

√

E dependence of the energy resolution and the Gaussian-like distri-

bution of ²

vis

(e).

For hadronic fully contained showers, the resulting visible-energy distribution is

almost Gaussian (deviations may occur in the tail of the distribution [Fabjan et al.

(1977)]) with a peak located at the position of the mean visible-energy. However,

generally the energy resolution does not scale as 1/

√

E. Therefore in hadronic

calorimetry, the energy resolution is worsened.

In sampling calorimeters, only a small fraction of the visible energy is de-

posited in readout detectors. As in sampling electromagnetic devices, ﬂuctuations

in the number of crossed active samplers by ionizing particles and in the deposited

energy by collision loss processes mostly contribute to broaden the visible-energy

distribution and to build up the so-called sampling ﬂuctuations (e.g., [Amaldi

(1981); Wigmans (1987)]). Furthermore, a non-negligible fraction of the incoming

energy is invisible (see Sect. 3.3.1), since it is spent in processes like the nu-

clear break-up. Fluctuations in the amount of this invisible energy result in the

enlargement of the visible-energy distribution and constitute the intrinsic resolu-

tion (e.g., see [Amaldi (1981); Fabjan (1986); Wigmans (1987); Br¨uckmann et al.

(1988); Fesefelt (1988)]). These nuclear processes (as discussed in Sect. 3.3) are

not present in electromagnetic showers. In hadronic cascades, the visible energy,

vis

(π), is usually no longer proportional to the incoming hadron energy, since there

is always an electromagnetic component, whose fraction varies with the energy

(Sect. 3.3). This fraction, f

, undergoes ﬂuctuations on an event-to-event basis

(see Sect. 3.3.1 and, e.g., [Amaldi (1981); Fabjan (1985a, 1986); Wigmans (1987);

Fesefelt (1988); Wigmans (1988)]). As the e/π ratio becomes quite diﬀerent from

1 (i.e., as the calorimeter becomes less and less compensating), the contribution,

of ﬂuctuations of a non-Gaussian nature, to f

is more and more important and

aﬀects the 1/

√

E behavior of the energy resolution. This latter one, in turn, be-

comes related to the e/π ratio [Amaldi (1981); Wigmans (1987)]. In Figs. 9.28 and

9.29, measured hadronic energy resolutions are shown for a calorimeter employing

hydrogeneous readout [Catanesi et al. (1987); HELIOS Collab. (1987); Acosta et al.

(1991)] and for silicon readout [SICAPO Collab. (1996)]. The data indicate

that

the calorimeter energy resolution scales as 1/

√

E, but an additive term is present for

non compensating calorimeters. This term increases, as expected, as the calorimeter

becomes less and less compensating.

The energy resolution σ(E)/E of a sampling hadron calorimeter (when instru-

These data were conﬁrmed by other measurements, e.g., see [Bleichert et al. (1987); Baumgart

et al. (1988a); Ros (1991); Wigmans (1991); Fabjan (1995b); SICAPO Collab. (1995a,b)] and

references therein.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

698 Principles of Radiation Interaction in Matter and Detection

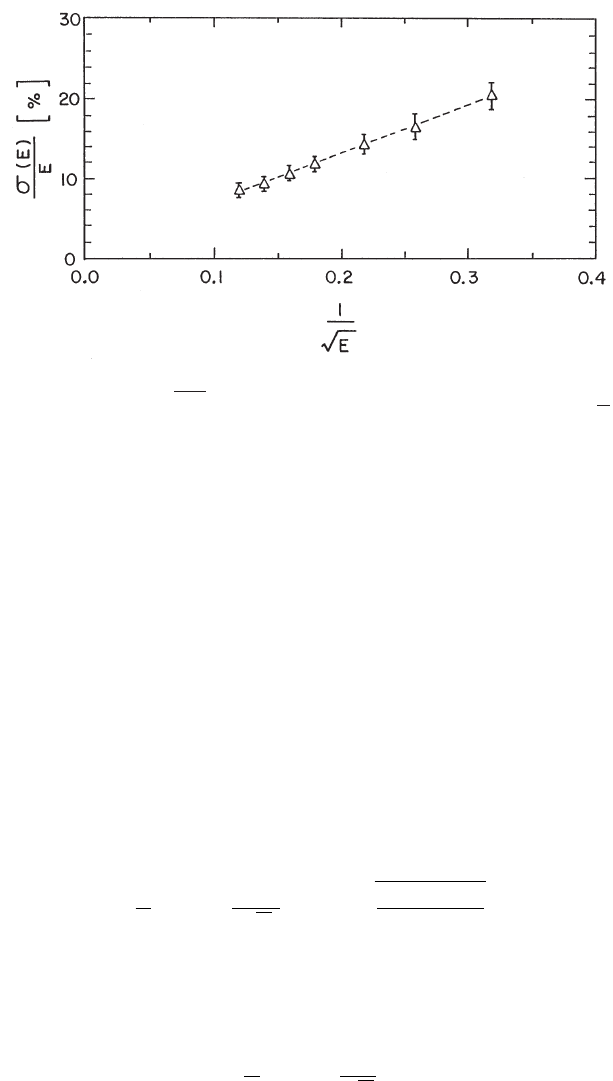
Fig. 9.28 Energy resolution σ(E)/E in [%] measured by calorimeters with hydrogeneous detectors

as a function of 1/

√

E, where E is the incoming hadron energy in GeV (from [Leroy and Rancoita

(2000)]): uranium/scintillator (◦) compensating calorimeter [HELIOS Collab. (1987)]; data cor-

rected for eﬀects of light attenuation from the lead/scintillating ﬁber (•) calorimeter [Acosta et al.

(1991)] (with e/π ∼ 1.1 at 10 GeV), uranium/scintillator (2) calorimeter [Catanesi et al. (1987)]

(with e/π ∼ 0.8 at 10 GeV). The lines are to guide the eyes.

mental contributions can be neglected) is expressed as [Wigmans (1987, 1988, 1991)]:

σ(E)

√

+ φ(e/π), (9.77)

where E is the incoming hadron energy in GeV;

intr

+ σ

samp

contains the contributions from the intrinsic resolution (σ

intr

), mostly due to nuclear

binding energy-losses, and from the sampling ﬂuctuations (σ

samp

), added in quadra-

ture; the function φ(e/π) takes into account eﬀects related to non compensation;

and, ﬁnally,

C = C

+ φ(e/π)

√

In Eq. (9.77), the function φ(e/π) is called the constant term and dominates the

energy resolution at high energy, since C

is almost independent of energy. Expe-

rimental data show that φ(e/π) vanishes, when the compensation condition is

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Principles of Particle Energy Determination 699

Fig. 9.29 Energy resolution,

σ(E)

in [%], measured by an almost compensating PbFe–Si–PbFe

calorimeter and corrected for the eﬀects of visible-energy losses as a function of 1/

√

E, where

E is the incoming hadron energy in GeV (from [Leroy and Rancoita (2000)]; data from Table 1

of [SICAPO Collab. (1996)]). The line is to guide the eyes.

achieved, i.e., φ(e/π ∼ 1) ∼ 0. One can also ﬁt the experimental data to an expres-

sion that adds the scaling and the constant term in quadrature (see e.g., [Catanesi

et al. (1987); Young et al. (1989); Acosta et al. (1991); Fabjan (1995b)] and referen-

ces therein). However, it is interesting to note that WA80 Collaboration obtained

results, favoring Eq. (9.77) over a very wide range and up to high energies [Young

et al. (1989)].

As mentioned before, the small fraction of the energy sampled in the active sam-

plers is at the origin of sampling ﬂuctuations σ

samp

. Their contribution to the over-

all energy resolution [Eq. (9.77)] was measured [Fabjan et al. (1977)] for low-A and

high-A passive samplers and found to depend on the amount of energy lost in a pas-

sive sampler (e.g., see [Fabjan and Ludlam (1982)]). Further measurements [Tiecke

(1989); Drews et al. (1990)] have conﬁrmed such a dependence (e.g., [SICAPO Col-

lab. (1995a,b, 1996)]). The contribution to the energy resolution from sampling

ﬂuctuations can be written as [Drews et al. (1990)]:

samp

√

≈ 0.115

∆²

mip

[MeV]

, (9.78)

where ∆²

mip

is the energy deposited by a minimum ionizing particle (mip) in a pas-

sive sampler, whose thickness is supposed to be kept constant in the whole calorime-

ter. As an example, for hadron calorimeters with U samplers of 4 mm thickness, the

contribution of sampling ﬂuctuations to the overall energy resolution is:

samp

≈

0.33

√