Lin S.D. Water and Wastewater Calculations Manual

Подождите немного. Документ загружается.

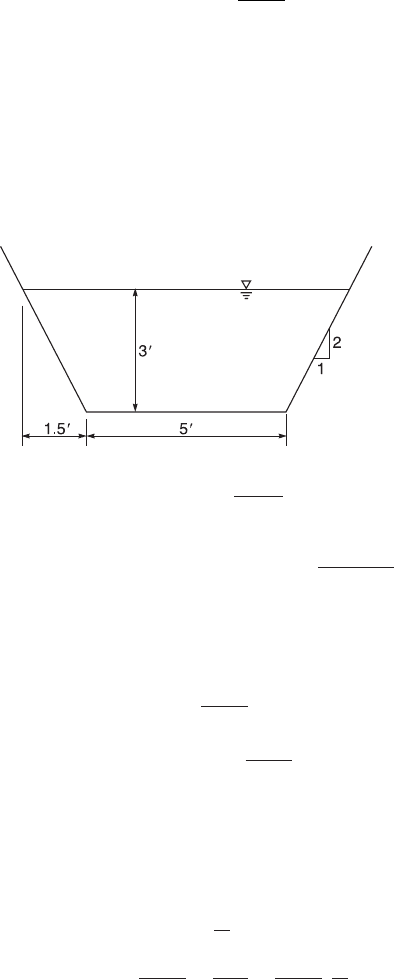
Example 2: A rock trapezoidal channel has bottom width 5 ft (1.5 m), water

depth 3 ft (0.9 m), side slope 2:1, n ⫽ 0.044, 5 ft wide. The channel bottom

has 0.16% grade. Two equal-size concrete pipes will carry the flow down-

stream. Determine the size of pipes for the same grade and velocity.

solution:

Step 1. Determine the flow Q

By the Manning formula, Eq. (4.36)

Step 2. Determine diameter of a pipe D

For a circular pipe flowing full, a pipe carries one-half of the total flow

67.9 5 1.424 D

8/3

135.8

1.486

0.013

2/3

s0.0016d

1/2

R 5

Q 5 A

1.486

2/3

1/2

5 19.5 3

1.486

0.044

s11.71d

2>3

s0.0016d

1/2

5 135.8 sft

/sd

5 11.71 ft

R 5 5 ft 1 2 21.5

1 3

5 19.5 ft

A 5

5 1 8

ft 3 3 ft

5 1500 s ft

/sd

5 45 3

1.486

0.016

s2.368d

2/3

s0.041d

1/2

Fundamental and Treatment Plant Hydraulics 275

Note: Use 48-in pipe, although the answer is slightly over 48 in.

Step 3. Check velocity of flow

Cross-sectional area of pipe A

This velocity is between 2 and 10 ft/s; it is thus suitable for a storm sewer.

4.3 Partially ﬁlled conduit

The conditions of partially filled conduit are frequently encountered in

environmental engineering, particularly in the case of sewer lines. In a

conduit flowing partly full, the fluid is at atm pressure and the flow is

the same as in an open channel. The Manning equation (Eq. (4.22)) is

applied.

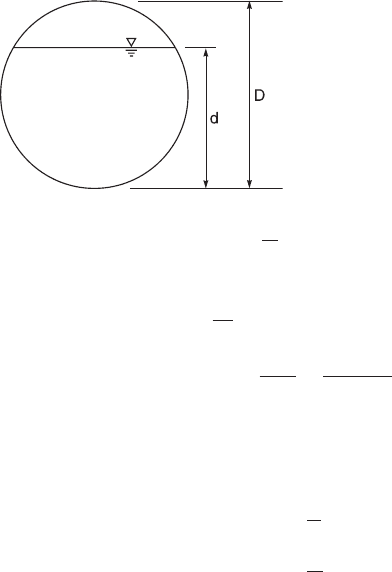
A schematic pipe cross section is shown in Fig. 4.7. The angle ␪, flow

area A, wetted perimeter P and hydraulic radius R can be determined

by the following equations:

For angle

(4.38a)

(4.38b)

u 5 2 cos

a1 2

cos

r 2 d

5 1 2

5 5.4 ft/s

V 5

67.9 ft

12.56 ft

ps4 ftd

5 12.56 ft

5 51.1 in

D 5 4.26 sftd

276 Chapter 4

Figure 4.7 Flow in partially

filled circular pipe.

Area of triangle ABC, a

Flow area A

(4.39)

For wetted perimeter P

(4.40)

For hydraulic radius R

R ⫽ A/P

Thus we can mathematically calculate the flow area A, the wetted

perimeter P, and the hydraulic radius R. In practice, for a circular con-

duit, a chart is generally used which is available in hydraulic textbooks

and handbooks (Chow, 1959; Morris and Wiggert, 1972; Zipparo and

Hasen, 1993; Horvath, 1994).

Example 1: Assume a 24-in diameter sewer concrete pipe (n ⫽ 0.012) is

placed on a slope of 2.5 in 1000. The depth of the sewer flow is 10 in. What is

the average velocity and the discharge? Will this grade produce a self-

cleansing velocity for the sanitary sewer?

solution:

P 5 pD

360

A 5

360

sin u

360

2 2 a

sin u

A 5

360

2 2a

sin u

a 5

AB BC 5

r sin

r cos

sin u

Fundamental and Treatment Plant Hydraulics 277

Step 1. Determine ␪ from (Eq. (4.38a), referring to Fig. 4.7 and to the

figure above

Step 2. Compute flow area A from Eq. (4.39)

Step 3. Compute P from Eq. (4.40)

Step 4. Calculate R

R ⫽ A/P ⫽ 1.24 ft

/2.805 ft

⫽ 0.442 ft

Step 5. Determine V from Eq. (4.22a)

5 3.591 sft/sd

5 123.83 3 0.58 3 0.05

1.486

0.012

s0.442d

2/3

s2.5/1000d

1/2

V 5

1.486

2/3

1/2

P 5 pD

360

5 3.14 3 2 ft 3

160.8

360

5 2.805 ft

5 1.24 sft

5 1.40 2 0.16

a3.14 3

160.8

360

sin 160.8

A 5

360

sin u

D 5 24 in 5 2 ft

u 5 160.8

5 cos

s0.1667d 5 80.4

5 0.1667

cos

5 1 2

2 3 10

278 Chapter 4

Step 6. Determine Q

Q ⫽ AV ⫽ 1.24 ft

⫻ 3.591 ft/s

⫽ 4.453 ft

Step 7. It will produce self-cleaning since V > 2.0 ft/s

Example 2: A concrete circular sewer has a slope of 1 m in 400 m. (a) What

diameter is required to carry 0.1 m

/s (3.5 ft

/s) when flowing six-tenths full?

(b) What is the velocity of flow? (c) Is this a self-cleansing velocity?

solution: These questions are frequently encountered in sewer design engi-

neering. In the partially filled conduit, the wastewater is at atm pressure and

the flow is the same as in an open channel, which can be determined with the

Manning equation (Eq. (4.22)). Since this is inconvenient for mathematical cal-

culation, a chart (Fig. 4.4) is commonly used for calculating area A, hydraulic

radius R, and flow Q for actual values (partly filled), as opposed to full-flow

values.

Step 1. Find full-flow rate Q

(subscript “f ” is for full flow)

Given:

From Fig. 4.4

Step 2. Determine diameter of pipe D from the Manning formula

For full flow

5 0.147 m

0.68

0.1 m

0.68

5 0.68

5 0.60

Fundamental and Treatment Plant Hydraulics 279

For concrete n ⫽ 0.013

Slope S ⫽ 1/400 ⫽ 0.0025

From Eq. (4.22b):

Answer (a)

D ⫽ 0.455 (m)

⫽ 1.5 ft

Step 3. Calculate V

From Fig. 4.4

Answer (b)

V ⫽ 1.07 V

⫽ 1.07 ⫻ 0.903 m/s

⫽ 0.966 m/s

⫽ 3.17 ft/s

Step 4. For answer (c)

Since

V ⫽ 3.27 ft/s > 2.0 ft/s

it will provide self-cleansing for the sanitary sewer.

5 1.07

5 2.96 ft/s

5 0.903 sm/sd

0.013

0.455

2/3

s0.0025d

1/2

0.147 5 1.20 D

8/3

0.013

3 a

2/3

3 s0.0025d

1/2

Q 5 AV 5 A

2/3

1/2

V 5

2/3

1/2

280 Chapter 4

Example 3: A 12-in (0.3 m) sewer line is laid on a slope of 0.0036 with n value

of 0.012 and flow rate of 2.0 ft

/s (0.057 m

/s). What are the depth of flow and

velocity?

solution:

Step 1. Calculate flow rate in full, Q

From Eq. (4.22a)

Step 2. Determine depth of flow d

From Fig. 4.4

Step 3. Determine velocity of flow V

From chart (Fig. 4.4)

V ⫽ 1.13 ⫻ 2.96 ft/s

⫽ 3.34 ft/s

or ⫽ 1.0 m/s

4.4 Self-cleansing velocity

The settling of suspended mater in sanitary sewers is of great concern

to environmental engineers. If the flow velocity and turbulent motion

are sufficient, this may prevent deposition and resuspend the sediment

and move it along with the flow. The velocity sufficient to prevent

5 1.13

5 0.72

d 5 0.72 3 1 ft

5 0.72 ft

2.0

2.32

5 0.862

5 2.96 ft/s

5 2.32 sft

/sd

5 0.785 3 123.8 3 0.397 3 0.06

5 AV 5

1.486

0.012

2/3

s0.0036d

1/2

D 5 1 ft

Fundamental and Treatment Plant Hydraulics 281

deposits in a sewer is called the self-cleansing velocity. The self-cleansing

velocity in a pipe flowing full is (ASCE and WEF 1992):

for SI units

(4.41a)

for British units

(4.41b)

where V ⫽ velocity, m/s or ft/s

R ⫽ hydraulic radius, m or ft

n ⫽ Manning’s coefficient of roughness

B ⫽ dimensionless constant

⫽ 0.04 to start motion

⫽ 0.8 for adequate self-cleansing

s ⫽ specific gravity of the particle

⫽ diameter of the particle

f ⫽ friction factor, dimensionless

g ⫽ gravitational acceleration

⫽ 9.81 m/s

or 32.2 ft/s

Sewers flowing between 50% and 80% full need not be placed on

steeper grades to be as self-cleansing as sewers flowing full. The reason

is that velocity and discharge are functions of attractive force which

depends on the friction coefficient and flow velocity (Fair et al. 1966).

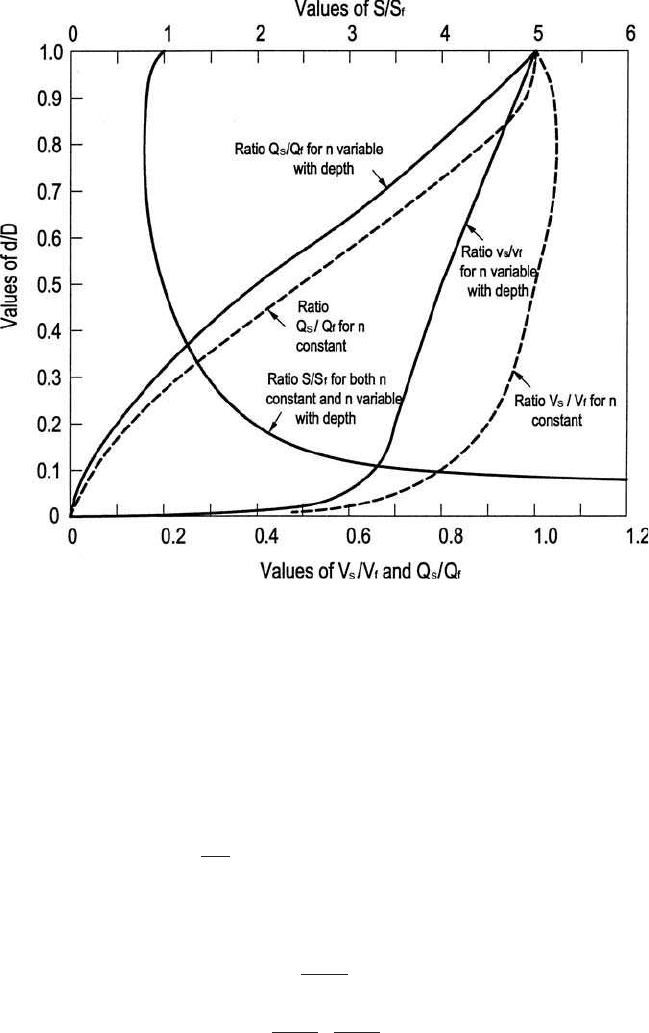
Figure 4.8 presents the hydraulic elements of circular sewers that pos-

sess equal self-cleansing effect.

Using Fig. 4.8, the slope for a given degree of self-cleansing of partly

full pipes can be determined. Applying Eq. (4.41) with the Manning

equation (Eq. (4.22)) or Fig. 4.3, a pipe to carry a design full discharge

at a velocity V

that moves a particle of size D

can be selected. This

same particle will be moved by a lesser flow rate between Q

and some

lower discharge Q

Figure 4.8 suggests that any flow ratio Q/Q

that causes the depth ratio

d/D to be larger than 0.5 requires no increase in slope because S

is less

than S

. For smaller flows, the invert slope must be increased to S

avoid a decrease in self-cleansing.

5 c

gss 2 1dD

1/2

V 5

1.486R

1/6

[Bss 2 1dD

]

1/2

5 c

gss 2 1dD

1/2

V 5

1/6

[Bss 2 1dD

]

1/2

282 Chapter 4

Example: A 10 in (25 cm) sewer is to discharge 0.353 ft

/s (0.01m

/s) at a self-

cleansing velocity. When the sewer is flowing full, its velocity is 3 ft/s (0.9m/s).

Determine the depth and velocity of flow and the required sewer line slope.

Assume N ⫽ n ⫽ 0.013.

solution:

Step 1. Determine the flow Q

and slope S

during full flow

Using the Manning formula

1.64 5

1.486

0.013

0.833

2/3

1/2

1.486

2/3

1/2

5 0.785 s10/12 ftd

3 3.0 ft/s

5 1.64 sft

/sd

Fundamental and Treatment Plant Hydraulics 283

Figure 4.8 Hydraulic elements of circular sewers that possess equal self-cleansing

properties at all depths.

Rearranging

Step 2. Determine depth d, velocity V

,and slope S for self-cleansing

From Fig. 4.8

For N ⫽ n and Q

⫽ 0.353/1.64⫽0.215, we obtain

d/D ⫽ 0.28

⫽ 0.95

and

S/S

⫽ 1.50

Then

d ⫽ 0.33D ⫽ 0.28 ⫻ 10 in ⫽ 2.8 in

⫽ 0.95 V ⫽ 0.95 ⫻ 3 ft/s ⫽ 2.85 ft/s

S ⫽ 1.5 S

⫽ 1.5 ⫻ 1.67‰ ⫽ 2.50‰

4.5 Speciﬁc energy

For a channel with small slope (Fig. 4.9) the total energy head at any sec-

tion may be generally expressed by the general Bernoulli equation as

(4.15)

where z is the elevation of the bed. For any stream line in the section,

P/␥ ⫹ z ⫽ D (the water depth at the section).

When the channel bottom is chosen as the datum (z ⫽ 0), the total

head or total energy E is called the specific energy (H

). The specific

energy at any section in an open channel is equal to the sum of the

velocity head (kinetic energy) and water depth (potential energy) at the

section. It is written as

(4.42a)

Since V ⫽ Q/A ⫽ flow/area, then

(4.42b)H

2gA

1 D

E 5

1 z

5 1.67‰

5 0.00167

1/2

5 0.04084

284 Chapter 4