Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов
Подождите немного. Документ загружается.


таны с помощью критериев случайности и в
результате
по-
лучено первое представление об исходном материале.
В качестве критериев случайности использовались: кри-
терий поворотных точек, критерий распределения длины
фазы,
критерий, основанный на знаках разностей, и крите-
рий,
основанный на ранговой корреляции. Подробнее об этих
критериях см., например, [120].
Критерий
поворотных точек состоит в подсче-
те числа пиков и впадин. Пиком называется наблюдение,
величиной более
двух
соседних;
впадина,
наоборот, — значе-
ние,
которое меньше
двух
соседних. Оба эти значения назы-
ваются
поворотными
точками.
Число поворотных точек в
исследуемом ряде сравнивается с их числом в совершенно
случайном ряде и на этом основании делается вывод, слу-
чаен ряд или нет. Проверка показала, что для
всех
рас-
сматриваемых рядов наблюдаемое число поворотных точек
существенно меньше, чем это
следует
теоретически для слу-
чайного ряда. Другими словами, данный критерий свиде-
тельствует
о том, что эти ряды не совсем случайны: в них
может быть скрыта некоторая закономерность движения
вперед.
Критерий
распределения длины фазы
предназначен для изучения распределения интервалов меж-
ду соседними поворотными точками, называемых
фазами.
Расчеты обнаружили заметные отличия теоретического рас-
пределения длины фазы у случайного ряда от тех, которы-
ми
обладают временные ряды валютных курсов. Для
всех
выбранных рядов характерно меньшее число коротких фаз
и
большее число более длинных фаз, чем для случайного
ряда, а также меньшее общее число фаз, т. е. фазы движе-
ния
курсов валют оказываются в среднем более продолжи-
тельными, и их смена происходит реже, чем у чисто случай-
ного ряда. Это наводит на мысль, что, несмотря на большую
колеблемость, движение валютных курсов генерируется
каким-то
инерционном механизмом, познание которого мог-
ло бы послужить известной базой для получения полезных
прогнозов.
Критерий,
основанный на знаках разнос-
тей, состоит в подсчете числа положительных разностей
первого порядка, иначе говоря, числа
точек
возрастания.
В основном этот критерий используется для проверки нали-
341

чия
линейного тренда. Здесь можно отметить некоторый
разброс наблюдаемого числа точек возрастания относительно
их теоретического числа. Так, швейцарский
франк
и британ-
ский
фунт имеют число точек возрастания меньше теорети-
ческого, а остальные валюты — больше. Однако весь заме-
ченный
разброс, хотя и на пределе, укладывается в 99%-ный
доверительный интервал. Это
свидетельствует
об отсутствии
четко выраженного устойчивого линейного тренда, но одно-
временно величина разброса
дает
основания предположить
наличие относительно долгосрочных
«кренов»
в ту или иную
сторону, что может быть полезным при прогнозировании.
Критерии,
основанные на ранговой кор-
реляции,
усиливают подозрение о наличии линейных трен-
дов у четырех из пяти валют за исключением фунта стер-
лингов.
Для британского фунта коэффициент т Кендэла
близок
к нулю, а для остальных валют положителен и су-
щественно отличен от нуля.
В целом проведенное изучение рядов валютных курсов
показало,
что, несмотря на сильную колеблемость ежеднев-
ных данных, они не являются совершенно случайными. В
них проявляется некоторая инерционность движения, и это
позволяет надеяться на применимость статистических ме-
тодов для прогнозирования курсов. В то же время их иссле-
дованные характеристики не очень сильно отличаются от
тех, которые теоретически выведены для совершенно слу-
чайного ряда. Вследствие этого нельзя ожидать от статис-
тических прогнозов большой степени осуществимости. Од-
нако
в совокупности за достаточно протяженный отрезок
времени они, по-видимому,
могут
оказаться полезными.
§ 3. АДАПТИВНАЯ МОДЕЛЬ
ПРОГНОЗИРОВАНИЯ ВРЕМЕННОГО РЯДА
С НЕУСТОЙЧИВЫМ
ХАРАКТЕРОМ
КОЛЕБАНИЙ
Исходя из того, что средний уровень ряда под-
вержен дрейфу, а флуктуациям относительно него присуща
сильная
изменчивость, при построении прогнозной модели
выбор был сделан в пользу класса адаптивных моделей.
Модель такого типа
всегда
находится в движении, впиты-
вает новую информацию и на основе ошибки прогноза на
342

предыдущем шаге корректирует свои параметры, подстра-
иваясь
к механизму, генерирующему временной ряд (под-
робнее см. гл. 1).
Нам
необходим прогноз курса валюты на следующий
день. Конечно, желательно знать и направление изменения
курса за день и его величину. Однако для получения поло-
жительного эффекта от валютных операций практически
достаточно предвидеть знак приращения курса валюты, т.е."
определить движение курса вверх или вниз. В связи с этим
для упрощения задачи сделаем некоторые преобразования
исходных рядов. Во-первых, от данных'*,,
#
2
,...,
x
N
перейдем
к
(ЛМ)-м первым разностям этого ряда Ax
v
...,
Ax
N
_
v
где
Д*,=
х
м
~ x
v
i
•=
1,2,...,
N— 1. Затем сделаем замену разно-
стей на k
(
по
следующему
правилу:
Ряд Ä,£
2
,...,£
W
_,,
состоящий из единиц и нулей,
будем
для
краткости называть
знаковым
рядом.
Разумеется, упроще-
ние,
достигнутое переходом от исходного временного ряда к
знаковому, сопряжено с потерей части информации. По зна-
ковому
ряду,
например, ничего нельзя сказать об амплитуде
колебаний
исходного ряда. Однако несомненно, что в знако-
вом ряде основная информация о характере и последова-
тельности изменений курса валюты сохраняется, причем в
самом рафинированном виде, а исключается информация,
имеющая для нас второстепенное значение. Одним из след-
ствий такого преобразования исходной статистической базы
является то, что довольно-таки сложный вопрос о наличии
тренда и его использовании при прогнозировании в этом слу-
чае переходит в
другую
плоскость и сводится к изучению
закономерности чередования или сохранения знаков.
Знако-
вый ряд, очевидно, более адекватен поставленной задаче.
Итак,
имеется ряд, характеризующий динамику валют-
ного курса, состоящий из
-1,
0 и
+1.
Требуется определить,
каким
будет
следующее
значение этого ряда. Для прогно-
зирования
временного ряда обычно строится модель, отра-
жающая свойства генерирующего его механизма. В основу
343

прогнозной
модели в данном
случае
положим гипотезу об
инерционности
действий основной массы участников валют-
ной
игры. Разумеется, мы не рассматриваем периоды нару-
шения
обычной жизни валютного рынка внезапными круп-
ными
чрезвычайными событиями.
В сущности,
могут
быть лишь три ситуации. Первая,
когда основной массой участников валютного рынка ожи-
дается неизменное движение курса, и их совместные дей-
ствия
через спрос и предложение способствуют сохранению
знака
прироста курса. Вторая, когда большинством иг-
роков
предполагается изменение направления движения кур-
са и массовый характер валютных операций в предвидении
этого действительно вызывают перемену.знака прироста кур-
са. Третья, когда не ожидается ни роста, ни падения, и
индифферентность
к
валюте
оставляет ее курс в неопреде-
ленном
состоянии.
Направление ее движения в
будущем
аб-
солютно случайно. О нем заранее ничего нельзя сказать.
Модель должна уловить, какая именно из
трех
ситуаций
превалирует в последнее время, и исходя из гипотезы, что
она
сохранится по крайней мере в течение еще одной едини-
цы
времени,
дать
прогноз на следующий момент.
Построение
модели начнем с рассмотрения произведе-
ния
7/1,=
£,£,-г
Легко заметить, что
Первое
равенство в этом выражении
соответствует
со-
хранению тенденции движения курса при
переходе
от одно-
го момента к
другому,
третье
- смене тенденций, т.е. в этом
случае
речь идет о поворотной точке, а второе — неопреде-
ленной
ситуации.
Заметим,
что т, описывает движение курса лишь на еди-
ничном
интервале от точки i—l к точке L Для того чтобы
выяснить,
какая же ситуация чаще встречается в после-
днее время, целесообразно каким-то образом усреднить ряд
т
1
за известный интервал. Для этого применим метод экс-
поненциального
сглаживания.
344

Экспоненциальное
сглаживание ряда т. осуществляет-
ся
по рекуррентной формуле
(15.1)
где5
/
—
значение экспоненциальной средней в момент t;
ос — постоянная сглаживания (параметр адаптации), 0 <
ее
^ 1,
ß -
1
- а.
Свойства экспоненциальной средней подробно рассмот-
рены в гл. 1.
Выражение
(15.1)
можно переписать как
(15.2)
Здесь S
M
можно рассматривать как прогноз на один
шаг вперед, т.е. как прогноз величины m
t
, сделанный в мо-'
мент
*—1,
тогда
величина {m
t
— S
M
) есть погрешность это.го
прогноза, а новый прогноз S
t
получается в
результате
кор-
ректировки предыдущего прогноза с
учетом
его ошибки. В
этом и состоит адаптация прогнозной модели. Наилучшее
значение а легко устанавливается методом проб и поиска
минимума потерь или максимума выигрыша.
Приняв
во внимание, что
и
Нет
рудно убедиться в том, что S
(
есть не что иное, как адап-
тивный коэффициент корреляции, рассмотренный в гл. 9.
Ясно,
что значение 5,, являющееся результатом
усред-
нения
единиц и нулей,
будет
дробным числом из интервала
Ы, 1], поэтому прогноз т на момент Я-1
будем
определять
так:
345

Положительный знак
tfi
M
означает сохранение того зна-
ка
прироста, который имел место в момент t, а отрицатель-
ный
- перемену. Прогноз знака прироста курса валюты на
момент Н-1 определим как
Обратим внимание на то, что эта модель способна в раз-
личное время отражать то положительную, то отрицатель-
ную корреляцию соседних приростов- Она время от време-
ни,
приспосабливаясь к наблюдениям, как бы меняет свои
свойства на противоположные. Перейдем теперь к практи-
ческим испытаниям этой модели.
§
4.
ПРОГНОЗИРОВАНИЕ
КУРСОВ
ВАЛЮТ
Прежде всего нужно выбрать критерии, по кото-
рым
будем
судить
о полезности работы прогнозной модели.
Критерии
оценки результатов испытаний.
Нас,
разумеется,
будет
интересовать не только точность про-
гнозов,
но и получаемый от них удельный экономический эф-
фект.
Поэтому при расчете критериев условно
будем
считать,
что объем операций с данной валютой (т.е. объем ее покупки
или
продажи) равен 1 дол. США в день. Если прогноз оказал-
ся
правильным, то выигрыш равен разности Ц
+
,—*J.
а если
прогноз ошибочен, то \х
м
-х\
будет
уже размером ущерба.
Учитывая, что исследуемому статистическому материа-
лу присущи сильные стохастические колебания, в основе
критериев оценки результатов положим средний (на базо-
вом периоде) выигрыш (или проигрыш) от операций с ва-
лютой за единицу времени (т.е. за день) в расчете на один
доллар или совокупный выигрыш за определенный период
функционирования
модели. Кроме того, целесообразно рас-
считывать и некоторые
другие
абсолютные и относительные
показатели. Вот перечень критериев, которые мы использу-
ем в наших экспериментах:
346

L
— число оправдавшихся прогнозов знака прироста кур-
са валюты, т.е. число выигрышей;
М — число ошибочных прогнозов знака прироста, т.е.
число проигрышей;
PL
= [L/(L +
Л1)]100%
- процент оправдавшихся про-
гнозов знака прироста;
РМ = [M/(L +
М)]Ю0%
- процент ошибочных прогнозов
знака
прироста;
SPR
- сумма выигрышей (т.е. суммируются только вы-
игрыши) в валютных операциях за весь исследуемый пери-
од функционирования прогнозной модели, который
будем
обозначать через Т (измеряется в национальной валюте);
SLOS
— сумма потерь в валютных операциях за период
Т
(в национальной валюте);
SPR-SLOS - сальдо, сумма чистого выигрыша (в наци-
ональной
валюте);
R=SPR/SLOS - отношение суммы выигрышей к сумме
потерь;
REL=SPR/(SPR
+ SLOS)100% - процент реализован-
ных возможностей (SPR + SLOS - максимально возмож-
ный
выигрыш).
Эксперимент № 1. Проведем испытание изложен-
ной
выше адаптивной модели.
Всего
имеется 150 точек ряда.
Адаптируем
нашу модель, например, на первых 20 точках,
которые принимаем за статистическую
базу
модели. Число
20 выбрано, строго говоря, произвольно; основные сообра-
жения,
которыми мы руководствовались, состоят в том, что
за 20 шагов влияние на прогноз начального значения прак-
тически исчезает. Сделаем прогноз 21-й точки. Затем сдви-
нем
базу
на один шаг вперед и прогоним модель от точки 2
До точки 21 и сделаем прогноз 22-й точки и т.д.
Всего
полу-
чим 130 прогнозов. Однако прежде чем получать прогноз,
будем
на каждой статистической базе из 20 точек методом
перебора определять наилучшее для данного этапа значе-
ние
а (из 10 значений от 0,1 до 1,0 с интервалом 0,1). Ре-
зультаты
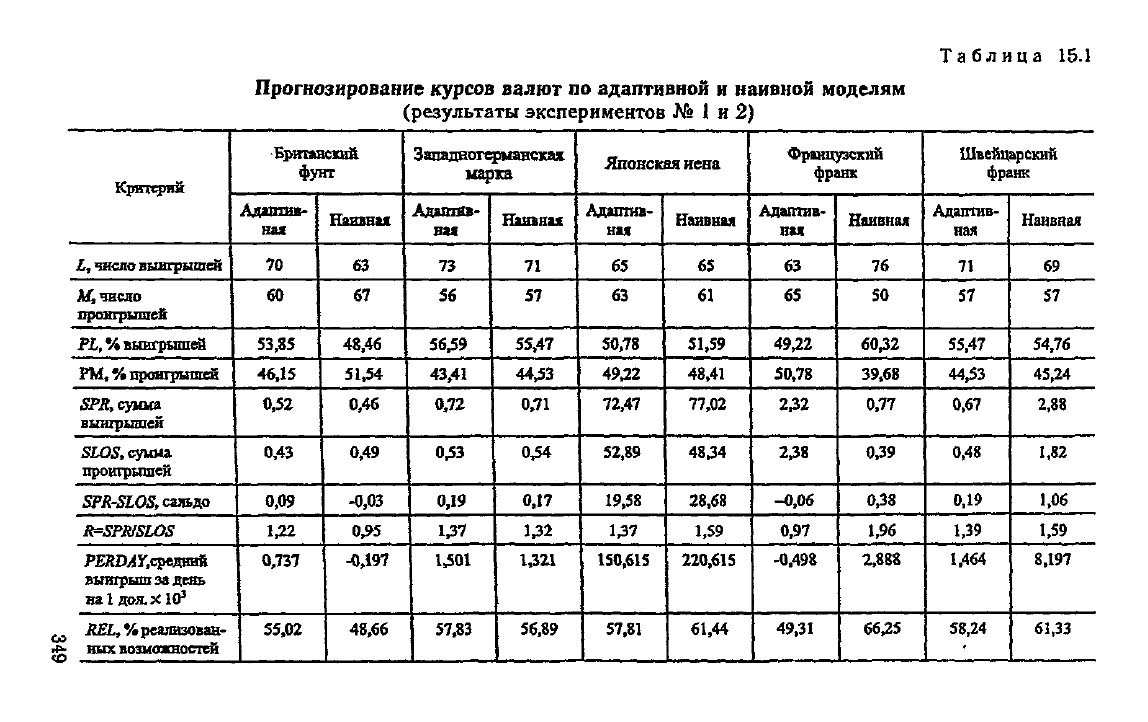
приведены в табл. 15.1, из которой видим, что по
четырем валютам (британский фунт, западногерманская
марка, японская иена, швейцарский франк) получена при-
быль, причем процент реализованных возможностей замет-
но
превышает 50%. Операции с французским франком при-
вели к некоторым потерям. Несколько слов нужно сказать о
347

показателе среднего выигрыша за день. Он, как правило,
представлен очень малым числом. Однако если речь идет
не
об одной операции в 1 дол., а об операциях на крупную
сумму
в течение большого числа дней, то суммарный выиг-
рыш достигнет значительной величины.
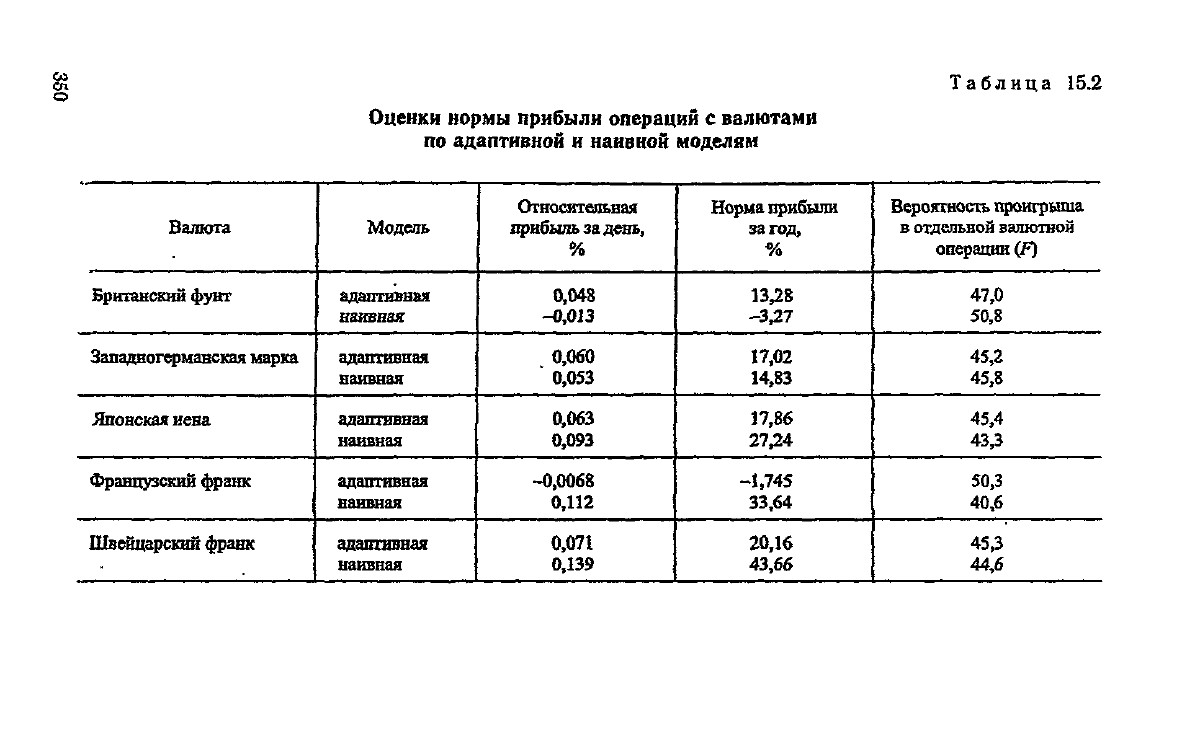
Сделаем теперь оценку результатов валютных операций
в
пересчете на
годовую
норму прибыли. Для этого отнесем
средний выигрыш за день к среднемууровню курса данной
валюты за исследуемый период (т.е. к среднему значению
130 последних точек) и получим относительную прибыль г
за один день. Будем считать, что в
году
260 рабочих дней
(имеются в
виду
рабочие дни банков). Тогда за год норма
прибыли составит [(1 + г)
260
- 1] • 100%. Результаты расче-
тов по этой формуле приведены в табл. 15.2. Как видим, по
всем валютам, кроме французского франка, получены вполне
положительные итоги. По французскому франку понесены
относительно небольшие убытки.
Хотелось бы также оценить, насколько устойчив поло-
жительный
результат
в отдельно взятой валютной опера-
ции,
велика ли зависимость от выпадения благоприятного
случая. Для измерения относительной устойчивости возьмем
математическое ожидание выигрыша и стандартное откло-
нение
от него. Исходя из предположения, что результаты
подчиняются нормальному закону распределения, вычис-
лим площадь под кривой распределения, находящуюся в
области отрицательного аргумента (т.е. определим вероят-
ность проигрыша). Эту площадь обозначим через F. Нахо-
дить ее
будем
приближенно по известным таблицам, а вы-
ражать в процентах. Отметим, что показатель PERDAY
является оценкой математического ожидания выигрыша, а
аргументом для определения F по таблицам нормального
распределения
будет
отношение
PERDAY/a,
где а - стан-
дартное отклонение выигрыша от его математического ожи-
дания.
Значения F также приведены в табл. 16.2, и они сви-
детельствуют
о том, что в каждой конкретной валютной
операции
вероятность проигрыша весьма велика.
Эксперимент № 2. Теперь получим прогноз по наи-
вным
моделям. Будем различать два типа так называемых
наивных моделей. Согласно модели первого типа все время
предполагается, что прирост курса в следующий момент
будет
таким же по знаку, что и в текущий момент. В модели
348
Таблица
15.1
Прогнозирование
курсов
валют
по адаптивной и
наивной
моделям
(результаты
экспериментов
№
1
и 2)
СО
Критерии
L,
число
выигрышен
М,
число
проигрышей
PL,
*/%
выигрышей
РМ,
% проигрышей
•SPÄ,
сумма
выигрышей
SLOS,
сумма
проигрышей
SPR-SLOS,
сальдо
R=SPR/SLOS
PERDAY,cpcMBB&
выигрыш
за день
на
1
дол. X10*
REL,
% реализован-
ных
возможностей
Британский
фунт
Адашив~
ная
70
60
53,85
46,15
0,52
0,43
0,09
1,22
0,737
55,02
Наивна*
63
67
48,46
51,54
0,46
0,49
-0,03
0,95
-0,197
48,66
Западногерманская
марка
Адапгяв-
яах
73
56
56,59
43,41
0,72
0,53
0,19
1,37
1,501
57,83
Наивная
71
57
55,47
44,53
0,71
0,54
0,17
1,32
1,321
56,89
Японская
иена
Адаптив-
нах
65
63
50,78
49,22
72,47
52,89
19,58
1,37
150,615
57,81
Наивная
65
61
51,59
48,41
77,02
48,34
28,68
1,59
220,615
61,44
Французский
франк
Адаптив-
ная
63
65
49,22
50,78
2,32
2,38
-0,06
0,97
-0,498
49,31
Наивная
76
50
60,32
39,68
0,77
0,39
0,38
1,96
2,888
66,25
Швейцарский
франк
Адаптив-
ная
71
57
55,47
44,53
0,67
0,48
0,19
1,39
1,464
58,24
Наивная
69
57
54,76
45,24
2,88
1,82
1,06
1,59
8,197
61,33
ел
О
Оценки
нормы прибыли операции с валютами
по
адаптивной и наивной моделям
Таблица
15.2
Валюта
Британский
фунт
Западногерманская марка
Японская иена
Французский франк
Швейцарский франк
Модель
адаптивная
наивная
адаптивная
наивная
адаптивная
наивная
адаптивная
наивная
адаптивная
наивная
Относительная
прибыль за
день,
%
0,048
-0,013
0,060
0,053
0,063
0,093
-0,0068
0,112
0,071
0,139
Норма прибыли
за год,
%
13,28
-3,27
17,02
14,83
17,86
27,24
-1,745
33,64
20,16
43,66
Вероятность
проигрыша
в
отдельной
валютной
операции (F)
47,0
50,8
45,2
45,8
45,4
43,3
50,3
40,6
45,3
44,6
