Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов
Подождите немного. Документ загружается.

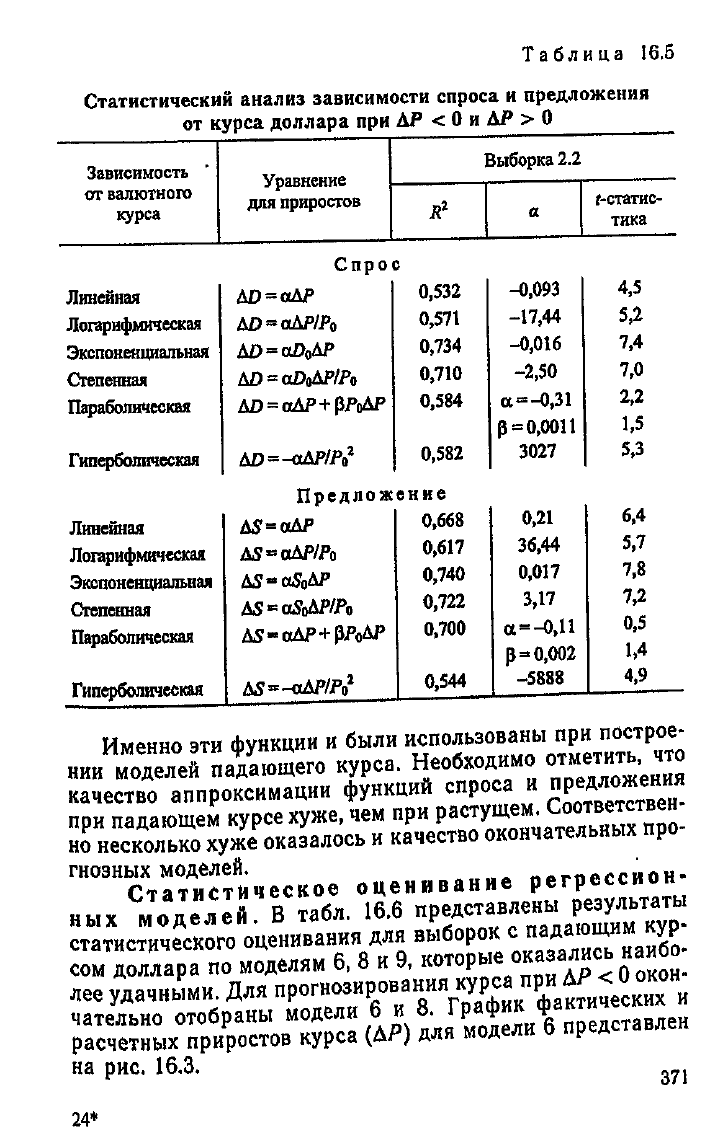
Таблица
16.5
Статистический
анализ
зависимости
спроса
и
предложения
от
курса
доллара
при АР < 0 и АР > О
Именно
эти функции и были использованы при построе-
нии
моделей сдающего курса. Необходимо отметить что
качество аппроксимации функций спроса и
npw«««™
пои
падающем курсе
хуже,
чем при растущем. Соответствен-
но^
нескТьк?хуже
Р
оказалс;сь
и
качество окончательных про-
гнозных моделей
оценивание
регрессион-
ных
моде«!
В табл. 16.6 представлены результаты
ст
Ь
т'истТче^огГоцени/ания для выборок сп
=
кУР;
сом доллара по моделям 6, 8
и
9, вторые оказались аибо
лее удачными. Для прогнозирования курса приiAP>< 0
окон
чательно
отобраны
модели^6
и
8.
JP^JJ
Ф
а
™^SeH
расчетных
приростов
курса
(АР)
для
модели
о
пред
на
рис. 16.3.
37
j
24*
Зависимость
от валютного
курса
Линейная
Логарифмическая
Экспоненциальная
Степенная
Параболическая
Гиперболическая
Линейная
Логарифмическая
Экспоненциальная
Степенная
Параболическая
Гиперболическая
Уравнение
для приростов
Выборка
2.2
Я
г
Спрос
М)~аАР1Р
а
AD-аДАР
ДО
=
аДАР/Ро
AD
=
aAP
+
ßP(AP
ДО=-аАР/Р
0
2
0,532
0,571
0,734
0,710
0,584
0,582
Предложение
AS=aAP
AS-aAP/Pa
AS=a5
0
AP
AS
=
a5oAP/Po
AS-otAP
+
ßPoAP
AS=-aAP/Po
2
0,668
0,617
0,740
0,722
0,700
0,544
a
-0,093
-17,44
-0,016
-2,50
a=-0,31
ß
=
0,0011
3027
0,21
36,44
0,017
3,17
a=-0,ll
ß
=
0,002
-5888
г-статис-
тика
4,5
5,2
7,4
7,0
2,2
1,5
5,3
6,4
5,7
7,8
7,2
А С
0,5
1,4
4,9

Таблица
16.6
Результаты
оценивания регрессионных моделей
на различных выборках при АР <
О
Модель
б
8
9
Выборка
2.1
2.2
2.1
2.2
2.2
Параметры
и
критерии
качества
0,860
0,871
0,860'
0,870
0,857
21,9
24,8
22,0
25,1
27,5
DW
2,14
2,18
2,17
2,15
2,16
ос
-0,030
-0,030
4605
-4,517
4151
'а
3,4
3,2
3,3
3,1
2,3
ß
0,014
0,014
0,161
0,016
3,406
Ч
3,5
з,з
4,7
4,4
4,2
cor(a,ß)
0,836
0,834
0,783
0,776
0,823

Рис. 16.3,
Фактические (кривая со светлыми кружочками)
и
расчетные (кривая с черными кружочками) снижения
курса доллара для
Модели
6 при.ЛЯ <
О
§
6. ОЦЕНКА
КАЧЕСТВА
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
Анализ устойчивости параметров.
Проблема устойчивости параметров регрессионных моде-
лей
-
одна
из
ключевых при эконометрическом прогнозиро-
вании.
Если параметры устойчивы,
то при
использовании
соответствующей модели можно рассчитывать
на
получе-
ние
достаточно достоверного прогноза,
в
противном случае
прогноз может оказаться ошибочным, если
не
предусмотре-
на
корректировка
и
адаптация параметров.
Значения
параметров
аир для
моделей
4
(выборка
АР
> 0)
и
6
(выборка
АР <
0), рассчитанные непосредствен-
но
по
формулам
для
приростов спроса
и
предложения
в
каждой точке, показали,
что в
обоих случаях
в
динамике
373

параметров
отсутствует
какая-либо тенденция, однако rtx
отклонения
от среднего уровня
могут
быть значительными.
Как
правило, наибольшие отклонения («всплески») имеют
место при сверхэластичной реакции банков, когда неболь-
шим
изменениям курса
сопутствуют
значительные сдвиги
в
спросе или предложении. Однако такие ситуации соот-
ветствуют
неординарным внешним условиям (всплеск инф-
ляционных
ожиданий, изменения в законодательстве и т.п.)
и
встречаются не очень часто. В нормальных же условиях
можно надеяться, что использование оценок а и ß в наших
моделях приведет к получению удовлетворительных про-
гнозов.
Оценка
точности
моделирования
курса.На
рис.
16.2 и 16.3 приведены фактические приросты курса (АР)
и
их прогнозы по моделям 4 и 6 для растущего и падающего
курсов (A/
3
mod
). Как видим, точность прогнозов сильно меня-
ется от торгов к торгам. Тем не менее средняя ошибка про-
гноза АР по каждой модели равна нулю — это вытекает из
способа оценивания параметров регрессионных моделей.
Поэтому требуется какой-то иной устойчивый показатель
точности, характеризующий качество прогнозов в среднем
по
выборке. Точность прогнозирования по регрессионным
моделям может оцениваться по-разному, в связи с чем рас-
смотрим несколько показателей.
Одним из них является
стандартная
ошибка
уравне-
ния. В наших моделях она представляется стандартной ошиб-
кой
прогноза прироста курса на
торгах.
В модели 4 она
равна о, = 5,33 руб., а в модели 6 о
2
= 4,58 руб.
Вызывает интерес также и
относительная
ошибка
про-
гноза.
Иногда для ее измерения
берут
отношение абсолют-
ной
ошибки модели к реальному значению объясняемой
переменной
(т.е. в нашем
случае
отношение модуля ошибки
к
реальному изменению курса на данных
торгах)
и
усред-
няют эту статистику по выборке. Однако здесь подобный
показатель не годится, так как если на
торгах
t ошибка
была отличной от нуля, а курс почти не изменился, то отно-
сительная ошибка
будет
очень большой, и это проявится
при
усреднении по всей выборке.
Для того чтобы получить представление об относитель-
ной
точности построенных регрессионных моделей, нами
374

предложен
другой
показатель, равный отношению суммы
ошибок
модели, взятых по модулю,
к
сумме модулей приро-
стов курса
за тот же
период:
где
Для модели
4
этот показатель
0
=
22,7%,
а для
модели
6
8=45,1%.
Еще одной характеристикой точности модели может быть
ошибка прогноза курса, равная ошибке прогноза прироста
курса,
так
как
P
t
=
Я
м
+
äP
t
, а
относительная погрешность
здесь может быть измерена статистикой
Для модели
4
X.,
- 1,85%, для
модели
6А,
2
а
2,15%.
Таким
образом, можно сделать следующие выводы.
1. Ожидаемая стандартная ошибка модельного прогно-
за равна
о,
=•
5,33, если курс растет, или
о
2
в
4,58, когда
он
снижается.
2. Относительный показатель ошибки моделирования
прироста курса
в
среднем
на
выборке равен 9,
=
22,7%
при
растущем курсе
и 6
2
=
45,1%
- при
падающем.
Это
свиде-
тельствует
о том, что
модели возрастающего курса можно
доверять
в
большей степени,
чем
модели снижающегося
курса, хотя
и
здесь ошибка достаточно велика.
3. Относительная ошибка прогноза абсолютного уровня
курса
в
среднем равна
Х
{
- 1,85%,
если
он
растет,
и \ -
2,15%,
когда
он
снижается.
375

§ 7. ВОЗМОЖНЫЕ СПОСОБЫ ИСПОЛЬЗОВАНИЯ
МОДЕЛЕЙ
Прогнозирование
курса накануне торгов
на
ММВБ.
Как
указывалось
в § 2
этой главы,
все
многообра-
зие
моделей торгов описывается
так:
(16.25)
где
коэффициент
A
t
в
общем
случае
не
является константой
и
может быть функцией
от
некоторых известных перемен-
ных
(в
частности, начального спроса
и
предложения банков
и
курса предыдущих торгов). Оценивание моделей заклю-
чается
в том,
чтобы
на
ретроспективном статистическом
материале
(на
данных
о
прошлых
торгах)
найти оценки ко-
эффициента
А
г
Получив
эти
оценки
на
основе регрессион-
ного
анализа, можно использовать
их для
прогнозирования
курса
на
предстоящих
торгах
в
зависимости
от
заявок бан-
ков
на
продажу
и
покупку,
а
также
от
различных вариан-
тов вмешательства
ЦБ РФ.
Регулирование курса с помощью интер-
венций
ЦБ РФ.
Центральный банк Российской Федера-
ции
является
на
торгах
регулирующим органом.
В
первой
половине
1992 г. его
функция выражалась
в
сдерживании
роста курса доллара,
а
впоследствии
- в
сглаживании
его
колебаний.
Возникала задача
—
оценить затраты ЦБ РФ
по
регулированию курса
и
выбору наилучшей стратегии.
Обратимся
к
выражению (16.25). Очевидно,
что
здесь
коэффициент
A
t
,
изменяющийся
во
времени, может быть
интерпретирован
как
мера чувствительности курса долла-
ра
к
интервенциям ЦБ РФ, показывающая, какое снижение
курса доллара приходится
на
единицу продаж
ЦБ РФ на
торгах
t, так как
(16.26)
В связи
с
этим динамика
A
t
представляет интерес.
В ре-
зультате
можно сделать важное заключение:
чем
выше
А,,
тем большего эффекта
(при
прочих равных условиях)
дос-
тигнут продажи
ЦБ РФ.
376

Отметим, что, если переписать
(16.25)
в виде
(16.27)
где A
t
определяется типом модели, то можно получать оценки
величины интервенции ЦБ РФ, необходимой для удержания
изменения
курса в заданных пределах.
В данной
главе
достаточно подробно изложен порядок
построения модели валютных торгов на ММВБ. Начав с
простейшей модели с постоянным параметром Л, постепен-
но,
на основе анализа с использованием микроэкономичес-
ких подходов, были получены альтернативные модели с пе-
ременным параметром А. Это привело к новой задаче -
проблеме идентификации, т.е. к выбору наилучшей модели.
Такой
выбор был сделан на основе статистических показа-
телей качества моделей. Насколько нам известно, эти мо-
дели несколько лет использовались для практических целей
регулирующими органами.
Разумеется, статистическая модель описывает наиболее
устойчивые связи переменных. У эксперта информации го-
раздо больше, поэтому последнее решающее слово остается
за экспертом, за «лицом, принимающим решение», а стати-
стические модели можно рассматривать как инструмент
получения дополнительной информации об интересующем
объекте или процессе.

ЗАКЛЮЧЕНИЕ
Заканчивая
рассмотрение адаптивных методов
прогнозирования,
отметим их некоторые особенности. Суть
адаптации состоит в том, что модель
следует
за процессом.
Это обусловливает отставание изменений в модели от но-
вых тенденций в реальном процессе, и чем больше время
упреждения, тем больше несоответствие
между
прогнозом
и
фактическим значением ряда. Следовательно, модели рас-
сматриваемого класса можно рекомендовать для получе-
ния
в рсновном краткосрочных прогнозов.
Многие из рассмотренных моделей характеризуют связь
между
исследуемой величиной и временем. Это обстоятель-
ство само по себе является довольно серьезным ограниче-
нием.
С
другой
стороны, время в модели выражает эволю-
цию всего комплекса условий протекания процесса. Через
время исходный ряд неявно связан с множеством взаимо-
связанных факторов,
учесть
влияние которых порознь зат-
руднительно. За счет упрощенного представления исследу-
емой величины, связанной с одним лишь фактором времени,
моделирование становится возможным
даже
при самой скуд-
ной
информации. Положительной чертой адаптивных мето-
дов является то, что с их помощью тщательно изучается
внутренняя
структура
временного ряда, взаимосвязь его
последовательных членов, а модели, являющиеся инстру-
ментом прогноза, чутко
реагируют
на динамические изме-
нения
и соответственно перестраиваются тем или иным об-
разом, учитывая обесценение устаревшей информации.
Сфера
применения адаптивных моделей одномерного
ряда довольно обширна. Они
могут
быть использованы для
прогнозирования
спроса и предложения, конъюнктурных
колебаний финансового рынка, отдельных экономических и
378

технико-экономических показателей, уровня запасов в сис-
темах
материально-технического снабжения, для прогнози-
рования
структурных
и технологических сдвигов, для опре-
деления траекторий некоторых глобальных показателей.
Наиболее простыми являются полиномиальные модели
Брауна. Их отличает ясность
концепции,
достаточная гибкость,
универсальность и простота расчетов. Особое значение имеют
адаптивные модели для
более
гибкого, чем обычно, выравни-
вания
рядов, очищения их от случайных наслоений. Однако
точность
получаемых
по ним прогнозов не
всегда
удовлет-
ворительна. Более строгим является метод, основывающий-
ся
на теории, разработанной Дж. Боксом и Г. Дженкинсом, -
метод
построения смешанных моделей авторегрессии-сколь-
зящего среднего. Имеются сведения [85], что, несмотря на
ограниченность используемой информации, модели Бокса -
Дженкинса в
деле
прогнозирования
могут
с
успехом
кон-
курировать со сложными эконометрическими моделями.
Очевидно, не случайно положительно показала себя в опы-
тах по прогнозированию экономических рядов и адаптив-
ная
модель авторегрессии (например, для прогнозирования
курсов валют), и адаптивная гистограмма (для анализа
кассовых остатков).
Рассмотренные в данном пособии методы анализа и по-
строения моделей изолированного временного ряда
могут
найти
применение и в качестве вспомогательного
средства.
Например,
для прогнозирования экзогенных переменных при
построении многофакторных моделей, а это очень важно,
так
как от точности прогноза экзогенных переменных зави-
сит
успех
прогнозирования по многофакторной модели в
целом.
Модели Бокса -Дженкинса можно также использовать
как
своеобразную
меру
динамических свойств ряда, и это
их качество положено в основу анализа эконометрических
систем линейных динамических уравнений. С помощью та-
ких моделей можно также получить ряды с некоторыми за-
ранее заданными автокорреляционными свойствами, что мо-
жет найти применение в имитационных
моделях.
Получил развитие адаптивный многомерный анализ:
разработаны адаптивный корреляционный и адаптивный
регрессионный анализ. Применение моделей АРСС для от-
ражения колебаний дисперсии регрессионных остатков при-
379

вело к появлению моделей с авторегрессионной условной
гетероскедастичностью. В экономике большую роль играют
циклические
колебания показателей. Колебания такого рода
имеют несистематический характер: у них переменные амп-
литуда
и период, деформированные положительная и отри-
цательная фазы. Для исследования подобных колебатель-
ных процессов нами предложен метод фазового анализа.
Этим,
однако, не ограничивается область использования
адаптивных моделей. Представим себе случай, когда для
отображения реального процесса построена какая-либо
сколь угодно сложная модель. Для
лучшего
ее согласова-
ния
с реальными данными можно в качестве корректирую-
щего элемента использовать
адаптивную
модель.
Ее на-
значение состоит в том, чтобы прогнозировать ошибку,
даваемую
основной моделью, и вносить
соответствующую
корректировку. Это значительно расширяет сферу приме-
нения
адаптивных моделей.
Тем не менее некоторые направления адаптивного моде-
лирования,
по-видимому, не находят широкого применения
в
экономических исследованиях по объективным причинам.
Например,
вызывает сомнение возможность плодотворного
развития метода, связывающего адаптивные свойства мо-
дели с изменениями в спектральных характеристиках дина-
мического ряда, так как оценки спектральной плотности,
определяемые на нескольких десятках точек, весьма нена-
дежны.
Как
мы видели, в адаптивном моделировании использу-
ется целый ряд подходов. Это обогащает арсенал исследо-
вателя, но одновременно создает трудности при выборе ме-
тода
в конкретном случае. Многие методы сравнительно
новые,
и поэтому еще не накоплен достаточный практичес-
кий
опыт работы с ними, в связи с чем в пособии особое
внимание
уделено изучению и сопоставлению свойств раз-
личных методов и моделей, что должно помочь делать пра-
вильный выбор с
учетом
целей и ресурсов исследователя.
Полагаем, что в условиях рыночной экономики адаптив-
ные методы экономических показателей являются наиболее
адекватным средством прогнозирования.
