Лукманов Р.Л. Каптелинина Ф.И. Методические указания и варианты контрольной работы
Подождите немного. Документ загружается.

БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ
Кафедра математики
Лукманов Р. Л. Каптелинина Ф. И.
Методические указания и варианты контрольной работы № 2
для студентов ОЗО
Специальность 660300 Агроинженерия
Уфа 2007
00УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией факультета механизации
сельского хозяйства (протокол № от 2005 года) и заседанием
кафедры математики (протокол № от 2005года)
Составители: доцент Лукманов Р.Л.
доцент Каптелинина Ф.И.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики
доцент Лукманов Р.Л.
Оглавление
Введение
1 Производная функции
1.1 Вопросы для самопроверки
2 Приложение производной к исследованию функции и построению ее графика
2.1 Вопросы для самопроверки
3 Неопределенный интеграл
3.1 Метод замены переменной
3.2 Интегрирование по частям
3.3 Интегрирование выражений, содержащих квадратный трехчлен
3.4 Интегрирование рациональных дробей
3.5 Вопросы для самопроверки
4 Определенный интеграл
4.1 Основные свойства определенного интеграла
4.2 Правила вычисления определенного интеграла
4.3 Приложения определенного интеграла
4.3.1 Вычисление площадей плоских фигур
4.3.2 Вычисление объемов вращения
4.3.3 Вычисление длины дуги кривой
4.1 Вопросы для самопроверки
5 Индивидуальные задания для контрольной работы №2

1 Производная функции
Понятие производной функции является одним из основных понятий в
математике. Производная широко применяется в различных областях науки и
техники. В частности, для вычисления скорости и ускорения различных процессов.
Производной функции y=f(x) в точке х
называется предел отношения
приращения функции к приращению аргумента, когда последнее стремится к нулю
произвольным образом.
x
y
xx
xfxf
у
xxx
0
'
lim
)()(
lim
.
Процесс отыскания производной называется дифференцированием функции.
Нахождение производной по определению является трудоемким процессом,
поэтому полезно вспомнить основные правила и формулы дифференцирования.
1. (с)
'
=0 2. (u+v)
'
=u
'
+v
'
3. (uv)
'
=u
'
v+uv
'
4. (сu)
'
= сu
'
5.
2
''
'
v
uvvu
v
u
6. Особый интерес представляет производная сложной функции.
Если у=f(u), где u=
)(х
, тогда у
'''
xuх
uy
.
Производные основных элементарных функций:
1.
1'
)(
nn
nxх
, в частности:
2
'
''
11
;
2
1
)(;1
x
х
x
хx
;
2.
aaa
x
ln)(
'
, в частности:
xx
ee
'
)(
;
3.
ax
x
a
ln
1
)(log
'
, в частности:
x
x
1
)(ln
'
;
4.
xx cos)(sin
'
; 5.
xsin(cos)
'
;
6.
x
tgx
2
'
cos
1
)(
; 7.
x
сtgx
2
'
sin
1
)(
;
8.
2
'
1
1
)(arcsin
x
x
; 9.
2
'
1
1
)(arccos
x
x
;
10.
2
'
1
1
)(
x
arctgx
; 11.
2
'
1
1
)(
x
arcctgx
.
Пример 1. Найти производную функции:
43
)2
1
( х
х
ху
.
Решение.
Используя правило дифференцирования сложной функции, а также формулу
нахождения производной сложной функции, получим:
)6
1
2
1
()2
1
(4)2
1
()2
1
(4
2
2
33'333'
x
x
x
x
x
xx
x
xx
x
xy
.
Пример 2. Найти производную функции
)1ln(2
23
xу
xctg
.
Решение.
Используем правило дифференцирования произведения двух функций.
'232'3'
))1(ln(2)1ln()2( xxy
xctgxctg
= =
'2
2
32'3
)1(
1
1
2)1ln()3(2ln2
x
x
xxctg
xctgxctg
= =
x
x
xx
x
xctgxctg
2
1
1
2)1ln()3(
3sin
1
2ln2
2
32'
2
3
=
1
2
2)1ln(
3sin
3
2ln2
2
32
2
3
x
x
x
x
xctgxctg
.
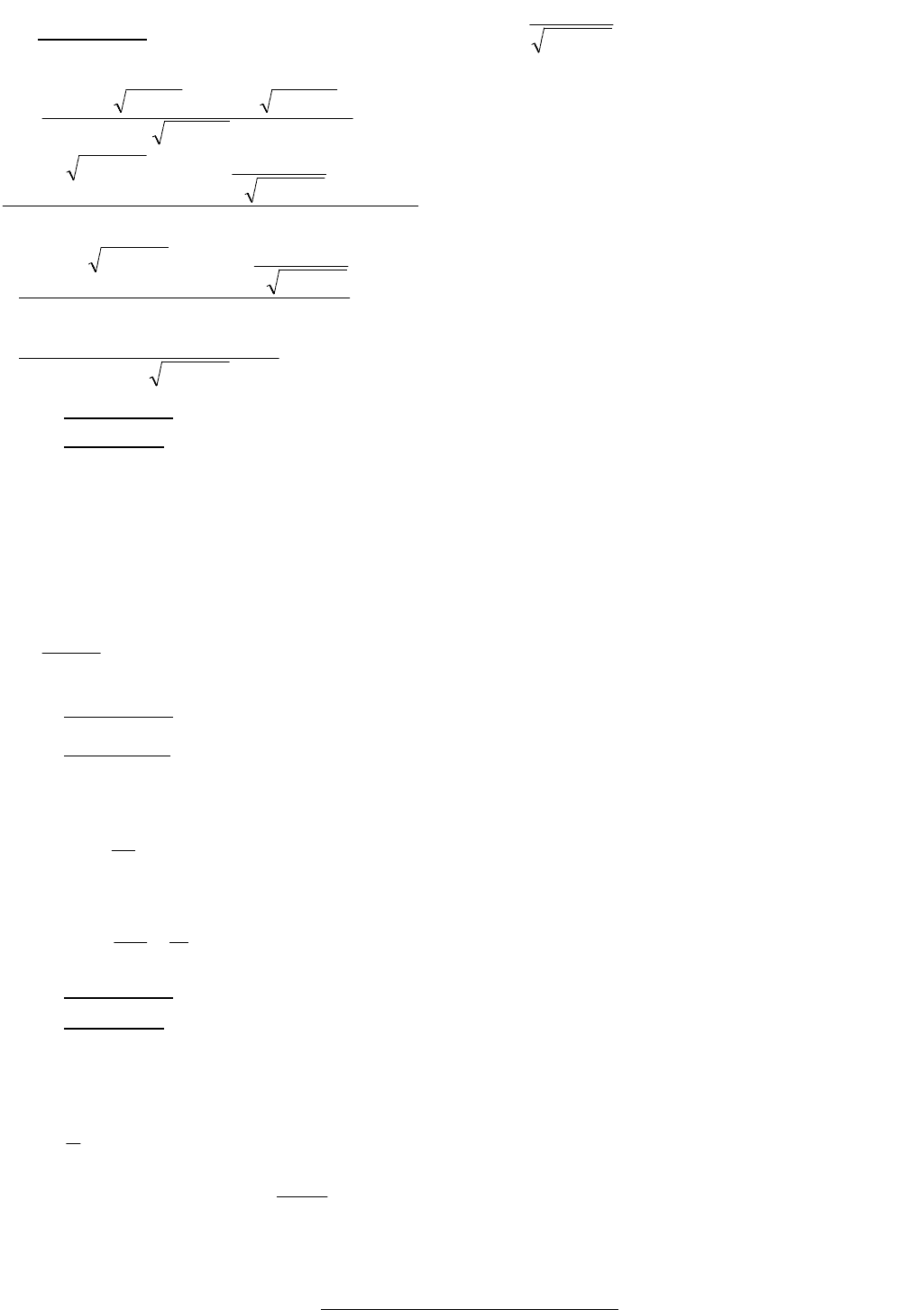
Пример 3. Найти производную функции:
3
32
2sin
x
x
у
.
Используем правило дифференцирования дроби.
23
'33'
'
)32(
)32(2sin2)2(sin
x
xxxx
y
=
.
32)32(
2sin9)32(2cos4
32
322
9
2sin322cos2
32
)32(
322
1
2sin3222
33
23
3
3
2
3
3
'3
3
3
xx
xxxx
x
x
x
xxx
x
x
x
xxxсos
Пример 4. Найти производную функции:
03
33
xyyx
.
Решение.
При дифференцировании неявно заданной функции необходимо рассматривать
«у» как функцию от «х» и дифференцировать как сложную функцию. Затем решить
полученное уравнение относительно у
'
.
).3(
.3333
.0)(333
2'2
'2'2
''22
yxyyx
yyxyyx
xyyyyx
.
2
2
'
yx
yx
y
Пример 5. Найти производную функции:
.
2
3
ty
tx
Решение.
При дифференцировании параметрически заданной функции используем
формулу
'
'
'
t
t
x
x
y
y
.
Найдем:
2'
3tx
t
,
ty
t
2
'
, тогда
t
t
t
y
x
3
2
3
2
2
'
.
Пример 6. Найти производную функции:
1
3
)3(sin
x
xy
.
Решение.
Используем метод логарифмического дифференцирования, т.е. вначале
логарифмируем выражение по основанию «е», потом дифференцируем и находим у
'
.
xxy 3sinln)1(ln
3
.
'3'3'
)3sin)(ln1(3sinln)1(
1
xxxxy
y
=
=
.3)1(33sinln333cos
3sin
1
)1(3sinln3
3232
xctgxxxx
x
xxx
1
3
3232'
)3(sin3)1(33sinln33)1(33sinln3
x
xxctgxxxyxctgxxxy
.
Вопросы для самопроверки
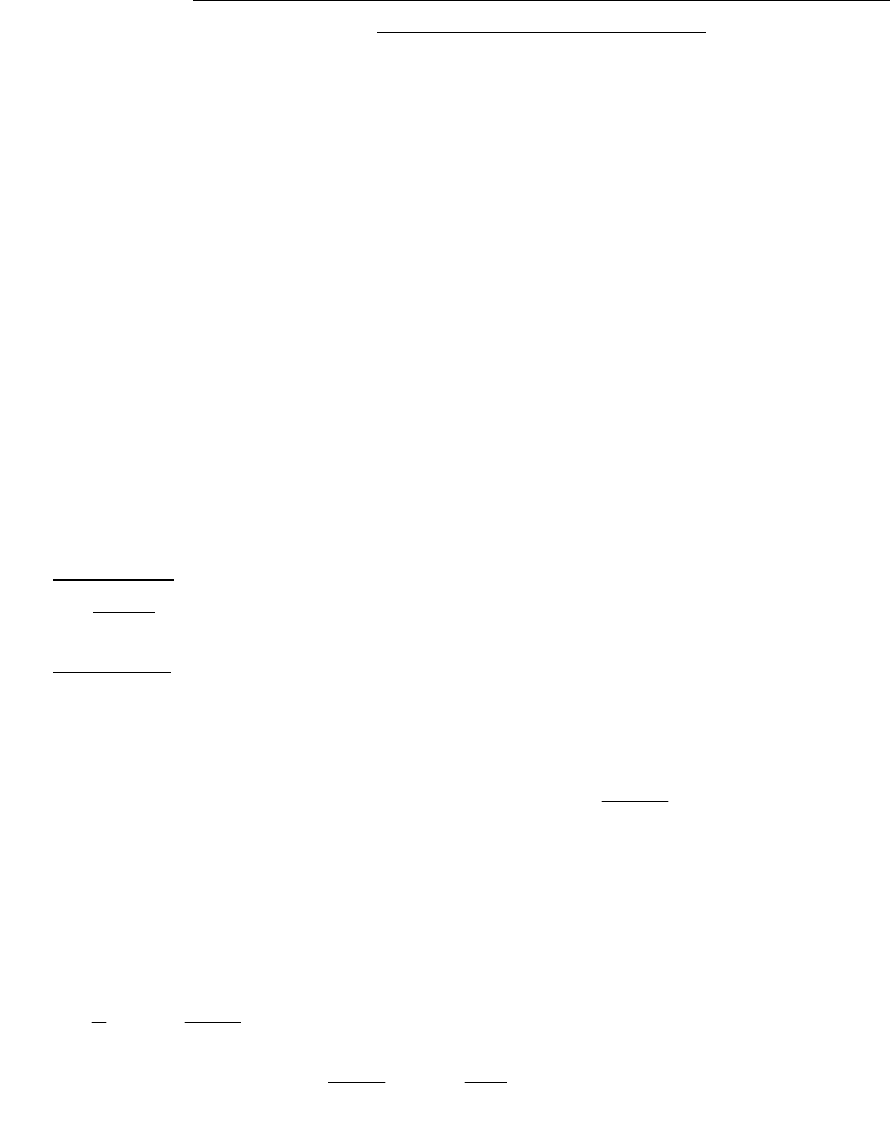
1. Что называется производной функции?
2. Каковы правила нахождения производных от суммы, произведения, дроби,
от постоянной величины?
3. Как найти производную сложной функции?
4. Правило дифференцирования функции, заданной неявно.
5. В чем заключается метод логарифмического дифференцирования?
2. Приложение производной к исследованию функции
и построению ее графика
Методы дифференциального исчисления позволяют исследовать функции и
строить их графики. Так, по знаку первой производной в интервале можно
определить возрастание (убывание) функции, делать выводы о наличии или
отсутствии экстремума функции. По знаку второй производной выделяем интервалы
выпуклости (вогнутости) графика функции и точки перегиба ее графика.
При исследовании функции и построении ее графика полезно воспользоваться
следующей схемой:
1. Найти область определения функции.
2. Определить четность или нечетность функции.
3. Найти точки пересечения графика с осями координат, если это возможно.
4. Найти асимптоты графика функции.
5. Найти интервалы монотонности и точки экстремума функции.
6. Найти интервалы выпуклости и вогнутости и точки перегиба графика
функции.
На основании полученного исследования построить график.
Пример 7. Исследовать функцию и построить ее график:
2
1 x
x
y
.
Решение.
1. Найдем область определения функции. Это будет вся числовая ось, кроме
точек, в которых знаменатель обращается в 0.
1x
.
);1()1;1()1;( x
.
2. Функция является нечетной, т.к.
)(
1
)(
2
xy
x
x
xy
, ее график
симметричен относительно начала координат.
3. Точка пересечения с осями координат:
0,0 уx
- начало координат.
4. Асимптоты графика:
а) вертикальные
.1x
б) наклонные
bkxy
, где
0
1
1
limlim
2
x
x
y
k
xx
.
.0
2
1
lim
1
limlim)(lim
2
x
x
x
ykxyb
xxxx
0y
-ось
x
при
x
.
5. Проведем полное исследование по первой производной.

.
)1(
1
)1(
21
)1(
)1(1
1
22
2
22
22
22
'22
'
2
'
x
x
x
xx
x
xxx
x
x
y
Нетрудно заметить, что при любом значении
х
области определения
функции, производная
0
'
у
, т.е. функция является всюду возрастающей. Точек
экстремума нет.
7. Проведем полное исследование по второй производной.
.
)1(
)3(2
)1(
)221)(1(2
)1(
)1)(2)(1(2)1(2
)1(
1
32
2
42
222
42
2222
'
22
2
''
x
xx
x
xxxx
x
xxxxx
x
x
y
0
''
y
при
0x
.
Выделим интервалы:
Точка
0x
является точкой перегиба графика функции
0)0(
.
пер
у
. Нанесем на
чертеж все полученные точки и линии.
2.2 Вопросы для самопроверки
1. Каковы признаки возрастания и убывания функции?
2. Что называется экстремумом функции?
3. Сформулируйте необходимые и достаточные признаки существования
экстремума функции.
4. Как найти интервалы выпуклости и вогнутости кривой и точки перегиба
графика функции?
5. Что называется асимптотой кривой?
6. Каких видов бывают асимптоты графика функции и как их найти?
3 Неопределенный интеграл
Функция
)(xF
называется первообразной функции
),(xf
если
).()(
'
xfxF
Множество первообразных функции
)(xf
называется
Cxfdxxf )()(
неопределенным интегралом и обозначается.
Операции дифференцирования и интегрирования взаимообратны:
)()(
'
xfdxxf
,
поэтому нетрудно получить следующую таблицу интегралов:
1)
C
n
x
dxx
n
n
1
1
(
1n
), 7)
Ctgx
x
dx
2
cos
,
2)
Cx
x
dx
ln
, 8)
Cctgx
x
dx
2
sin
,
3)
C
a
a
dxa
x
x
ln
, 9)
C
a
x
xa
dx
arcsin
22
,
4)
Cedxe
xx
, 10)
Ckxx
kx
dx
22
22
ln
,
5)
Cxxdx cossin
, 11)
C
a
x
arctg
axa
dx 1
22
,
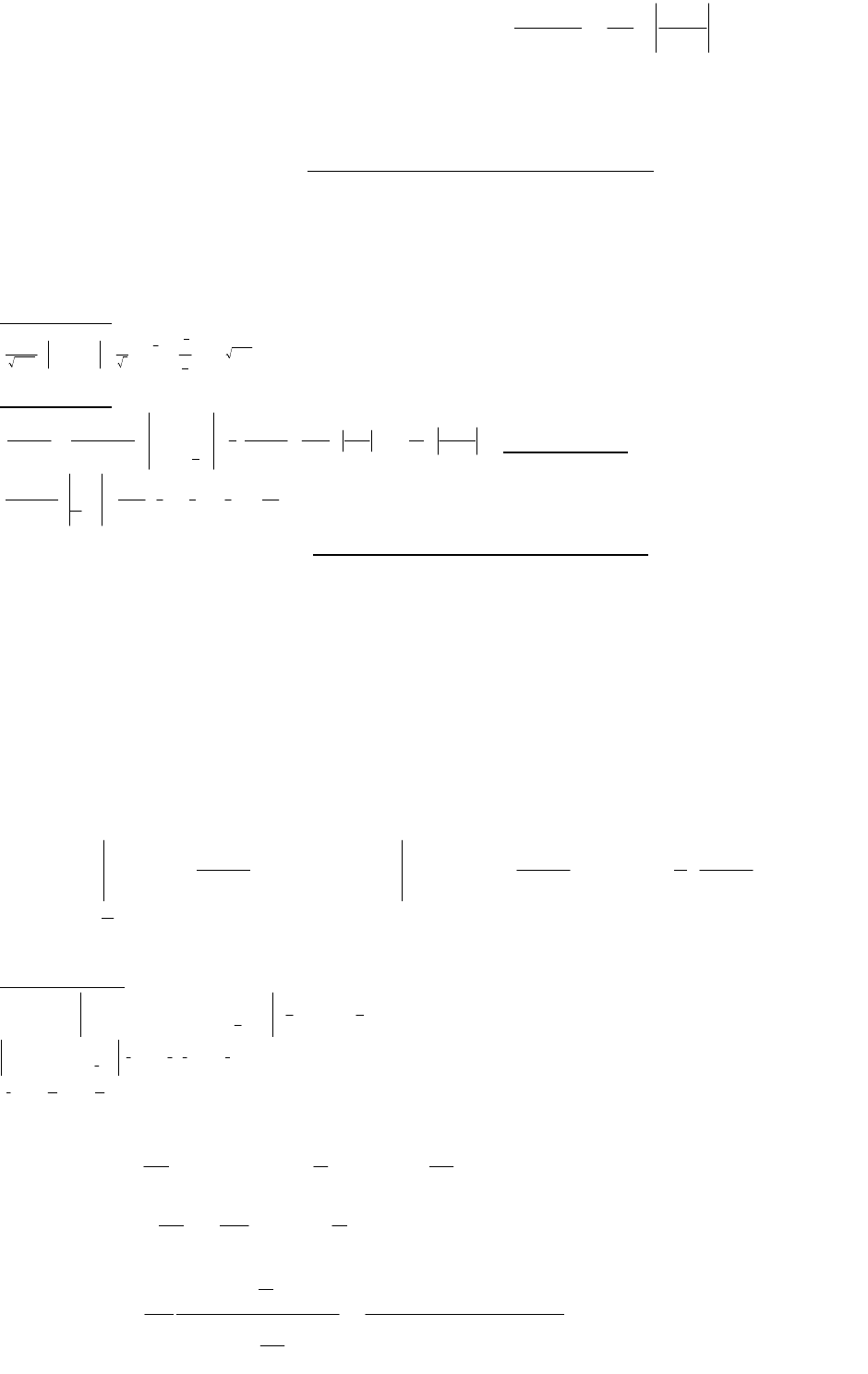
6)
Cxxdx sincos
, 12)
C
xa
xa
axa
dx
ln
2
1
22
.
Не ограничиваясь на непосредственном интегрировании по формулам, как на
простейшем способе решения примеров, перейдём сразу к более сложным методам.
3.1 Метод замены переменного
Пусть нужно найти неопределенный интеграл от непрерывной функции
).(xf
Если обозначить
)(tx
, то справедлива формула:
dtttfdxxf )()()(
'
.
Пример 8.
CxC
t
dtt
t
dt
dtxdx
tx
x
xdx
sin2
2
1
cos
sin
sin
cos
2
1
2
1
.
Пример 9.
C
x
x
C
t
t
nl
t
dt
dtdxx
dtdxx
tx
x
dxx
x
dxx
3
3
22
2
2
3
232
2
6
2
5
5
ln
30
1
5
5
103
1
5
3
1
3
1
3
)(525
Пример 10.
C
x
arctgC
t
arctg
t
dt
dt
x
dx
tx
xx
dx
2
ln
2
1
22
1
4
ln
)ln4(
22
.
3.2 Интегрирование по частям
Формула интегрирования по частям имеет вид:
vduuvudv
.
Можно выделить два класса интегралов, для которых применима эта формула:
I.
,
cos
sin)( dx
ax
ax
e
xP
ax
n
II.
dxxP
arcctgax
arctgax
ax
ax
ax
n
)(arccos
arcsin
ln
.
В первом случае
uxP
n
)(
, остаток
dv
, во втором случае, наоборот, первый
сомножитель обозначают
U
, а остаток
dvdxxP
n
)(
где
)(xP
n
– многочлен
постоянной степени от
x
.
Пример 11.
.)1ln(
2
1
1
2
2
1
1
.
1
.
,
2
222
Cxxarctgx
x
xdx
xarctgx
x
xdx
xarctgx
xdxvdvdx
du
x
dx
uarctgx
поэтомутипавторогоинтеграл
arctgxdx
Формула
интегрирования по частям хорошо срабатывает и в других случаях.
Пример 12.
bxdxe
b
a
bxe
b
bx
b
bxdxbdvbxdx
dudxaeue
bxdxe
axax
axax
ax
sinsin
1
sin
1
coscos
cos
.coscossin
1
coscos
1
sin
1
cos
1
sinsin
2
2
2
bxdxe
b
a
bxe
b
а
bxe
b
bxdxe
b
a
bxe
bb
a
bxe
b
bx
b
bxdxvdvbxdx
dudxaeue
axaxax
axaxax
axax
Перенесем все интегралы в левую часть. Получим:
.cossin
1
coscos
22
2
bxe
b
a
bxe
b
bxdxe
b
a
bxdxe
axaxaxax
).cos(sin1cos
2
2
bx
b
a
bx
b
e
b
a
bxdxe
ax
ax
.
)cossin(
1
)cos(sin
cos
22
2
2
ba
bxabxbe
b
a
bx
b
a
bx
b
e
bxdxe
axax
ax
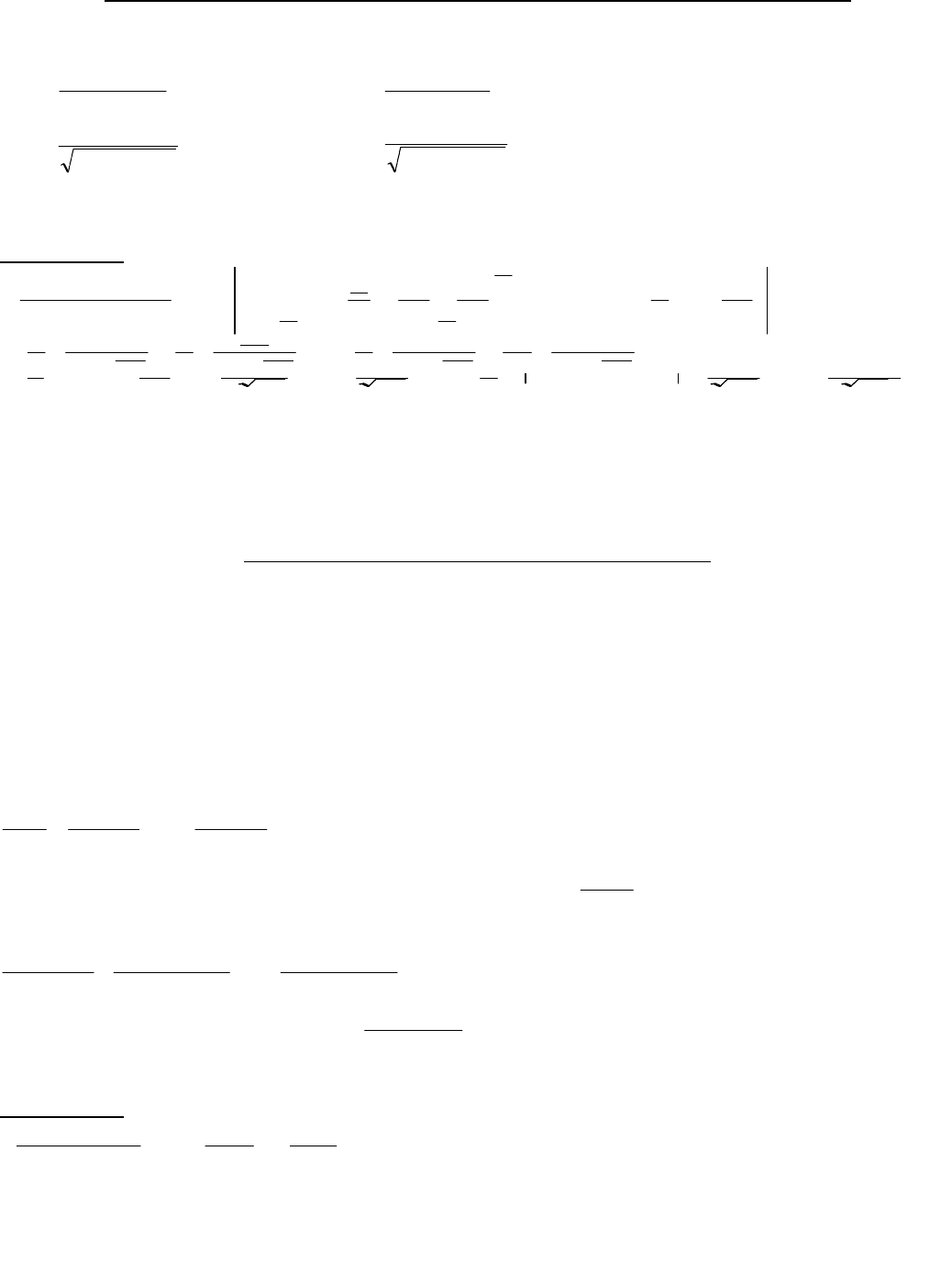
3.3 Интегрирование выражений, содержащих квадратный трехчлен.
К этому типу интегралов относятся интегралы вида:
;
2
1
cbxax
dx
J
dx
cbxax
BAx
J
2
2
;
cbxax
dx
J
2
3
;
.
2
3
dx
cbxax
BAx
J
Метод решения всех этих интегралов заключается в выделении полного квадрата в
знаменателе с последующей заменой переменной.
Пример 13.
.
55
54
55
31
1052ln
4
3
55
4
554
431
16
55
ln
1
3
16
55
4
31
16
55
2
4
6
16
55
2
31
2
1
16
55
2
3
,
4
5
,
4
5
16
55
4
5
2)5
16
25
16
25
2
2
5
2(2
5
2
5
(21052
1052
43
22
2222
2
2
22
2
c
x
arctgxxc
t
arctgt
t
dt
t
tdt
dt
tt
tdt
dtdxtxtx
xxx
xxxx
dx
xx
x
Интегралы видов
43
, JJ
решаются аналогично, только сводятся к другим табличным
интегралам.
3.4 Интегрирование рациональных дробей
Методика интегрирования правильных дробей основана на представлении
знаменателя в виде произведения линейных выражений и квадратичных
сомножителей с отрицательными дискриминантами.
В этом случае правильная рациональная дробь может быть представлена в виде
суммы простейших дробей, интегралы от которых легко находятся.
Каждому линейному сомножителю
k
ax )(
в знаменателе соответствует группа
простейших дробей вида:
.
)(
...
)(
2
21
k
k
ax
A
ax
A
ax
A
В частности при
1k
имеем только одно слагаемое
.
ax
A
Каждому квадратичному сомножителю
k
qpxx )(
2
соответствует дроби вида:
.
)(
...
)(
222
22
2
11
k
k
qpxx
BkxA
qpxx
BxA
qpxx
BxA
При
1k
имеем одно слагаемое
.
2
qpxx
BAx
Рассмотрим конкретные примеры вычисления интегралов от рациональных дробей.
Пример 14.
.
32)3)(2(
1
x
Bdx
x
Adx
dx
xx
x
После приведения к общему знаменателю получим следующее тождество для
числителей:
)2()3(1 xBxAx
, которым воспользуемся для нахождения коэффициентов
А
и
В
.
Подставим корни линейных сомножителей в знаменателе.

.
5
2
),23(13:3 BBx
.
5
3
),32(12:2 АAx
Таким образом, получим:
.3ln
5
2
2ln
5
3
35
2
25
3
)3)(2(
1
Cxx
x
dx
x
dx
dx
xx
x
Пример 15.
.
)1(1)1(
2
22
dx
x
C
dx
x
B
dx
x
A
dx
xx
x
Так же, как в предыдущем примере, будем иметь:
.)1()1(2
2
cxxBxxAx
Подставив корни знаменателя,
0x
;
1x
, найдем коэффициенты
А
и
C
.
.2,)10(2:0
2
AAx
.3,21:1 СCx
Для нахождения
""B
приравняем коэффициенты при одинаковых степенях левой и
правой частей тождества:
.2,,0:
2
ВАВВАx
Тогда
C
x
xx
x
dx
x
dx
x
dx
dx
xx
x
1
3
1ln2ln2
)1(
3
1
22
)1(
2
22
.
Пример 16.
.
13161)136)(1(
2
22
2
dx
xx
CBx
dx
x
A
dx
xxx
x
).1)(()136(2
22
xCBxxxAx
Подставим
1x
:
1-2=
.
20
1
,20 АA
Остальные неизвестные найдем, приравнивая коэффициенты при одинаковых
степенях:
.
20
27
2
20
1
13,132:0
.
20
21
20
1
1,1:
2
ССАx
ВBAx
Тогда
dx
xt
x
x
dx
dx
xxx
x
136
27
20
21
20
1
)136)(1(
2
22
2
dt
t
t
x
dtdx
txtx
xxx
dx
xx
x
x
dx
4
27)3(21
20
1
ln
20
1
3,3
4)3(136
136
2721
20
1
20
1
2
22
2
C
t
arctgtx
t
dt
dt
t
t
x
210
9
4ln
40
21
ln
20
1
45
9
4
2
40
21
ln
20
1
2
22
.
2
3
10
9
136ln
40
21
ln
20
1
2
C
x
arctgxxx
3.5 Вопросы для самопроверки
1. Что называется первообразной?
