Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Numerical Methods
75
cllxl
+
cI2xq
+
cI9xg
=
rl
C21XI
+
C?ZX2
+
c21x.9
=
r2
CllXl
+
C32X2
+
c1:<x9
=
r3
solving for the unknowns yields
rz
-
cPlxl
-
c2%xg
c
2'2
X?
=
By
making an initial guess for xl, x2, and xgr denoted as xy, x:, and x:, the value
of
x, on the first iteration is
Using the most recently obtained values for each unknown (as opposed to the
fixed point or Jacobi method), then
If the equations have the proper characteristics, the iterative process will
eventually converge. Commonly used convergence criteria are of two types:
1.
Absolute convergence
criteria
of
the form
are most useful when approximate magnitudes of xi are known beforehand
so
that
E
may be chosen to be proportional to x,.
2.
Relative convergence
criteria of the form
is
the choice if the magnitudes of xi are uncertain.

76
Mathematics
Relaxation
methods
may also be used to modify the value of an unknown before
it is used in the next calculation. The effect of the relaxation factor
h
may be seen
in the following equation, where
~("+l)'
is the value obtained at the present iteration.
and
0
<
h
<
2.
If
0
<
h
<
1,
the effect is termed underrelaxation, which is
frequently employed to produce convergence in a nonconvergent process. If
1
<
h
<
2,
the effect, overrelaxation, will be to accelerate an already convergent
process.
Least Squares Curve Fitting
For a function f(x) given only as discrete points, the measure of accuracy of
the fit is a function d(x)
=
I
f(x)
-
g(x)
1
where g(x)
is
the approximating
function to f(x). If this is interpreted as minimizing d(x) over all x in the interval,
one point in error can cause a major shift in the approximating function towards
that point. The better method is the least squares curve fit, where d(x) is
minimized if
is minimized, and for a polynomial of order m
E
=
x[ao+a,x, +a&+
. . .
+
a,xy
-
f(x,
)I'
,=I
Setting the partial derivatives of
E
with respect to each
of
the coefficients
of
g(x) equal to zero, differentiating and summing over
1,
.
.
.
,
n forms a set of
m
+
1
equations
[9]
so
that
If the preceding solution is reduced to a linear approximation (n
=
l),
the
matrix will be (n
=
1)
and for a parabola
(n
=
2),
the first three rows and columns.

Numerical Methods
77
Another possible form is the exponential function
F(t)
=
aeP‘
and although partial differentiation will produce two equations in two unknowns,
they will be nonlinear and cannot be written in matrix form. However, a change
in variable form may produce a model that
is
linear, for example, for the
preceding equation
In
(F)
=
In
(a)
+
Pt
and
if
X is defined to be t,
Y
to be In
(F),
a,
=
In
(a),
and a,
=
j3,
the equation
becomes
Y(x)
=
a,,
+
a,X
and linear least squares analysis may be applied.
In order to determine the quality (or the validity) of fit of a particular
function to the data points given, a comparison of the deviation of the curve
from the data to the size of the experimental error can be made. The deviations
(i.e., the scatter off the curve) should be of the same order of magnitude as
the experimental error,
so
that the quantity “chi-squared’’ is defined as
where
y,’
=
is the fitted function and
y,
is the measured value of
y
at xl,
so
that
Ay,
is the magnitude of the error of
y,’.
The sum is over n points and
if
the
number of parameters in the model function is g,, then if
0
(X’)
>
0
(n
-
g),
the approximating function is a poor fit, while if
0
(X2)
<
0
(n
-
g), the function
may be overfit, representing noise [lo].
The simplest form
of
approximation to a
continuous
function is some polynomial.
Continuous functions may be approximated in order to provide a “simpler form”
than the original function. Truncated power series representations (such as the
Taylor series) are one class of polynomial approximations.
The Chebyshev polynomials, T,(x) or Tn, which exist on the interval -1
I
x
I
1,
form the series
To
=
1
T,
=
x
(see Table 1-14 for a more complete list). If these polynomials are inverted,
powers of x are given in terms of T,(x) (Table 1-15). Any finite interval a
I
y
I
b
can be mapped onto the interval -1
I
x
I
1
by the formula
x
=
(2y
-
b
-
a)/(b
-
a)

78
Mathematics
Table
1-14
Chebyshev Polynomials
T,(x)
=
1
T,(x)
=
x
T,(x)
=
2~’- 1
T3(x)
=
4x3
-
3~
T,(x)
=
8x4
-
8x2
+
1
T6(x)
=
32x6
-
48x4
+
18X2
-
1
T,(x)
=
128~’
-
256x6
+
160~~
-
32~’
+
1
T,(x)
=
16x5
-
20x3
+
5x
T,(x)
=
64x7
-
112x5
+
56x3
-
7x
Table
1-15
Inverted Chebyshev Polynomials
1
=
To
x
=
T,
1
4
1
i(3To
+
4T,
+
T4)
1
-(10T,
+
5T,
+
T,)
16
1
-(lOTo
+
15T,
+
6T4
+
TJ
32
1
-(35T,
+
21T3
+
7T, +T7)
64
1
-(35T,
+
56T,
+
28T,
+
8T,
+
TJ
128
-w,
+
T3)
and the inverted Chebyshev polynomials can be substituted for powers of
x
in
a power series representing any function f(x). Since the maximum magnitude
for Tn
=
1
because
of
the interval, the sum of the magnitudes
of
lower-order
terms is relatively small. Therefore, even with truncation of the series after
comparatively few terms, the altered series can provide sufficient accuracy.
See also the discussion on cubic splines in “Interpolation.”
Numerical integration
By assuming that a function can be replaced over a limited range by a simpler
function and by first considering the simplest function, a straight line, the areas
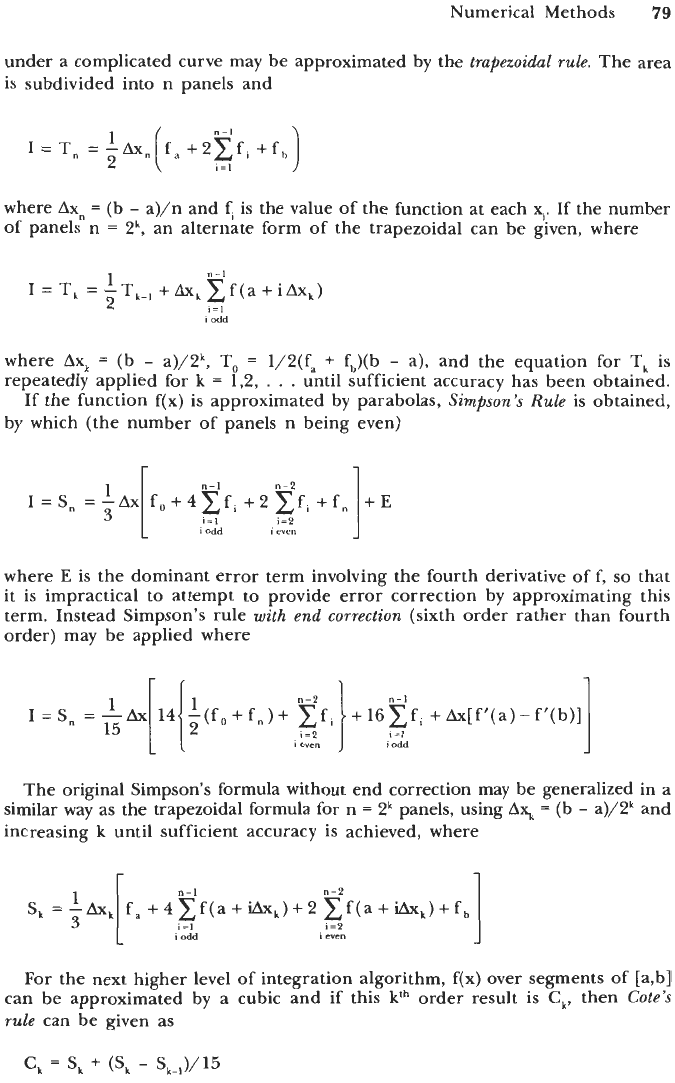
Numerical Methods
79
under a complicated curve may be approximated by the
is subdivided into n panels and
where
Axn
=
(b
-
a)/n and
f,
is the value of the function
of panels n
=
2', an alternate form of the trapezoidal
trapezoidal rule.
The area
at each xi. If the number
can be given, where
"-1
1
2
I=T, =-Tk_,+Axkxf(a+iAxk)
,=I
I
add
where
Ax,
=
(b
-
a)/2', To
=
1/2(fa
+
fJ(b
-
a), and the equation for
T,
is
repeatedly applied for
k
=
1,2,
. . .
until sufficient accuracy has been obtained.
If the function f(x) is approximated by parabolas,
Simpson's Rule
is obtained,
by which (the number of panels
n
being even)
r
1
"-1
n-2
I=S,
=-Ax
f,+4xf,+2xfL+f,
i=2
I
eYe"
3
I
;:id
where
E
is the dominant error term involving the fourth derivative off,
so
that
it is impractical
to
attempt to provide error correction by approximating this
term. Instead Simpson's rule
with
end correction
(sixth order rather than fourth
order) may be applied where
+Ax[f'(a)-f'(b)]
The original Simpson's formula without end correction may be generalized in a
similar way as the trapezoidal formula for n
=
2' panels, using
A3
=
(b
-
a)/2, and
increasing
k
until sufficient accuracy is achieved, where
1
n-2
i=l
i=2
i
odd
i
even
For the next higher level of integration algorithm, f(x) over segments of [a,b]
can be approximated by a cubic and if this
kth
order result is
C,,
then
Cote's
rule
can be given as
=
'k
+
('k
-

80
Mathematics
k
1
2
3
4
0
and the next higher degree approximation as
D,
=
c,
+
(C,
-
Ck_,)/63
The limit suggested by the sequence
T,
+
S,
+
C,
-+
D,
+
If a new notation Ti") is defined, where
k
is the order of the approximation
is known as
Romberg Integration.
(n
=
2k)
and m is the level of the integration algorithm, then
m
=
0
(trapezoidal rule)
T:")
=
T,
m
=
1
(Simpson's rule)
TL')
=
S,
m
=
2
(Cote's rule)
Ti2'
=
Ck
m=3
Tis)
=
D
etc.
The generalization of the preceding definitions leads to the Romberg equation
T(0)
TlO)
T!'
)
TIO)
TO)
Tp
TIO)
Th'
)
Tf)
T13)
T:")
Tb
T!
)
Tf)
Ti3)
The procedure is to start with the one-panel trapezoidal rule
1
2
To
3
Tf)
=
-(b-a)(f,
+f,)
and then increase the order
(k)
of the calculation by

Numerical Methods
81
Increasing accuracy may be obtained by stepping down or across the table,
while the most accurate approximation will be found on the lower vertex of the
diagonal. The Romberg procedure is terminated when the values along the
diagonal no longer change significantly, Le., when the relative convergence
criterion is less than some predetermined
E.
In higher-level approximations,
subtraction of like numbers occurs and the potential for round-off error
increases. In order to provide a means of detecting this problem, a value is defined
and since
R:")
should approach
1
as a limit, a satisfactory criterion of error is
if
Rim) begins to differ significantly from
1.
An improper integral has one or more of the following qualities
[38]:
1.
Its integrand goes
to
finite limiting values at finite upper and lower limits,
2.
Its upper limit equals
-,
or its lower limit equals
-00.
3.
It has an integrable singularity at (a) either limit, (b) a known place
but cannot be integrated right on one or both
of
these limits.
between its limits, or (c) an unknown place between its limits.
In the case of 3b, Gaussian quadrature can be used, choosing the weighting
function to remove the singularities from the desired integral. A variable step
size differential equation integration routine
[38,
Chapter
151
produces the only
practicable solution to 3c.
Improper integrals of the other types whose problems involve both limits are
handled by open formulas that do not require the integrand to be evaluated at
its endpoints. One such formula, the extended midpoint rule, is accurate to the
same order as the extended trapezoidal rule and is used when the limits of
integration are located halfway between tabulated abscissas:
Semi-open formulas are used when the problem exists at only one limit. At
the closed end of the integration, the weights from the standard closed-type
formulas are used and at the open end, the weights from open formulas are
used. (Weights for closed and open formulas of various orders of error may be
found in standard numerical methods texts.) Given a closed extended trapezoidal
rule
of
one order higher than the preceding formula, i.e.,
i=2
13
12
+f,)+-(f, +fn-,)+ Cfi
and the open extended formula of the same order of accuracy
i=4
7
+f,_l)+-(f,+f,-2)+Cfi
12

82
Mathematics
a semi-open formula can be constructed that, in this example, is closed on the
right and open on the left:
In order
to
eliminate the restriction
of
evenly spaced points,
Gauss
Quadrature
algorithms may be constructed. In these algorithms not only the function values
are weighted, but the position of the function evaluations as well as the set of
weight factors are left as parameters to be determined by optimizing the overall
accuracy. If the function is evaluated at points xl,,
xI,
. .
.,xn, the procedure has
2n
+
2
parameters
to
be determined (the xi, and the
wi
for each
xi)
and is
required to be accurate for any polynomial of degree
N
=
2n
+
1
or less.
These algorithms are frequently stated in terms of integrals over
[-1,1],
termed
Gauss-Legendre quadrature, and the general formula then is
(Ilf(x)dx
s
w,f,,
+
w,f,
+
.
.
.
+
w,f,
For example, for n
=
1,
For each choice
of
n (the number of points), the
wk
and the n zeros
(6,)
of
the nth degree Legendre polynomial must be determined by requiring that the
approximation be exact for polynomials of degree less than 2n
+
1.
These have
been determined for n
=
2
through
95
and an abbreviated table for some n is
given in Table
1-16.
The interval
-
1
S
6
I
1
is transformed onto the interval
a
5
x
S
b by calculating for each xk
(k
=
1,
. .
.,
n)
b+a
b-a
2
2
Xk
=
-
'-61,
and an approximation to the integral is then
2
wkf(xk)
b-a
I=-
2
k=l
Some other typical Gaussian quadrature formulas are:
1
(-131)
C
hebyshev
xce-x
Laguerre
(c
=
0,1,
.
.
.)
(OF-)
(-P)
e-x2
Herrnite

Numerical Methods
83
Table
1-16
Sampling Points and Weight Factors for Gauss Quadratures
n
i
5
WI
2
0
-0.5773502692
1
.oooooooooo
1
-0.5773502692
1
.oooooooooo
3 0 -0.7745966692 0.5555555556
1
0.0
0.8888888889
2
0.7745966692 0.5555555556
5
0
-0.9061 798459 0.2369268850
1
-0.53846931 01
0.4786286705
2
0.0
0.5688888889
3-4
see Note below
10
0
-0.9739065285 0.066671 3443
1
-0.8650633667 0.149451 3492
2
-0.6794095683 0.21 90863625
3
-0.4333953941 0.26926671 93
4
-0.1 488743390 0.2955242247
5-9
see
Note below
20
0
-0.9931 285992 0.0176140071
1
-0.963971 9273 0.040601 4298
2
-0.91 22344283 0.0626720483
3
-0.8391169718 0.083276741 6
4
-0.746331 9065 0.101 93011 98
5
-0.6360536807 0.11 81 945320
6
-0.51 08670020 0.1 31 6886384
7
-0.3737060887 0.1 420961 093
8
-0.227785851
1
0.1491 729865
9
-0.076526521
1
0,1527533871
10-1 9
see Note below
Note: Points and weight factors are symmetric with respect to zero.
Weights and zeros for the above formulas (and for other Gaussian formulas) may
be found in references such as Stroud
(Gaussian Quadrature Formulas,
Prentice-
Hall,
1966).
Since the dominant error term in Gauss Quadrature involves very high-order
derivatives, the best method for determining the accuracy of an integration is
to compare the results for several different n. However, in certain cases, a
comparison may result in a set of significantly different answers, due to the
presence of one or more singularities in
f(x)
or to a highly oscillatory function.
Also
if
very large values of n are employed, round-off error can cause a major
deterioration in accuracy (see previous discussion of Romberg integration)
Numerical Solution
of
Differential Equations
The two major categories of
ordinary differential equations
are
1.
Initial value problems
where conditions are specified at some starting value
of
the independent variable.

84
Mathematics
2.
Boundary value problems
where conditions are specified at two (or, rarely,
more) values of the independent variable.
(The solution of boundary value problems depends to a great degree on the
ability to solve initial value problems.) Any nLh-order initial value problem can
be represented as a system of n coupled first-order ordinary differential equa-
tions, each with an initial condition. In general
-_
dy2
-
f,(y,,y,,
f
.
.,y.
,t)
dt
and
YJO)
=
Y,(]?
y2(0)
=
Y?(]’
. .
?Y,,(O)
=
Y,,,,
The
Euler method,
while extremely inaccurate,
is
also extremely simple. This
method is based on the definition of the derivative
or
Y,,
=
Y,
+
f1Ax
where
f,
=
f(xL,y,) and y(x
=
a)
=
ylI
(initial condition).
Discretization error depends on the step size, i.e., if Ax,
+
0,
the algorithm
would theoretically be exact. The error for Euler method at step
N
is
0
N(Ax)~
and total accumulated error
is
0
(Ax), that is, it is a first-order method.
The
modified Euler method
needs two initial values
yII
and
y1
and is given by
Y”
=
y,.n
+
f”.1(2Ax)
+
0
(W2
If
ye
is given as the initial value,
yI
can be computed by Euler’s method, or
more accurately as
AYA
=
f(X,,,Y,,)AX
YI
=
Yo
+
AY.,
f,
=
f(XI>Y,)
and
Ayh
=
f,Ax
