Масленникова О.Е., Попова И.В. Основы искусственного интеллекта

Подождите немного. Документ загружается.

- 41 -

Высказывания типа I подчинены (следовательно, подразумевают)

высказываниям типа А.

Высказывания типа О подчинены высказываниям типа Е.

В то время как контрадикторные высказывания имеют

противоположные истинностные значения (одно истинно, другое ложно),

контрарные высказывания не могут быть одновременно истинными, но могут

быть одновременно ложными.

При помощи логического квадрата можно вывести противоположные,

противоречащие и подчиненные данным суждения, установив их истинность

или ложность.

Пример

1. Всякое суждение выражается в предложении А →1.

2. Ни одно суждение не выражается в предложении Е→ 0.

3. Некоторые суждения не выражаются в предложении О → 0.

4. Некоторые суждения выражаются в предложении I → 1.

Кроме того, с помощью логического квадрата Аристотеля, можно

устанавливать типы отношений между суждениями: 1) получения выводных

знаний; 2) сопоставления разных точек зрения по дискуссионным вопросам;

3) редактирования текстов и в других случаях.

Формализмы исчисления высказываний

В основе многих моделей представления знаний лежат формализмы

исчисления высказываний и предикатов. Строгое изложение этих теорий с

точки зрения классической математической логики содержится в работах

Шенфилда и Тейза, у Поспелова можно найти популярное изложение этих

теорий, которое можно рекомендовать как начальное введение.

По определению Тейза логические высказывания - это класс

предложений естественного языка, которые могут быть истинными или

ложными, а исчисление высказываний это раздел логики, который изучает

такие предложения. Возникает естественный вопрос: А как быть с

предложениями языка, об истинности которых нельзя сказать ничего

определенного?

Пример. «Если завтра пойдет дождь, то я останусь дома».

Пока просто будем считать, что все предложения, с которыми нам

приходится иметь дело, относятся к классу логических высказываний.

Высказывания будем обозначать прописными буквами латинского алфавита и

индексом, если этого потребует изложение. Образцы обозначения

высказываний: S, S1, S2, H, H1, H2.

Как уже отмечалось, логическое высказывание либо истинно, либо

ложно. Истинному высказыванию присваивается логическое значение

- 42 -

ИСТИНА (или И), ложному - логическое значение ЛОЖЬ (или Л). Таким

образом, значение истинности образует множество {И,Л}.

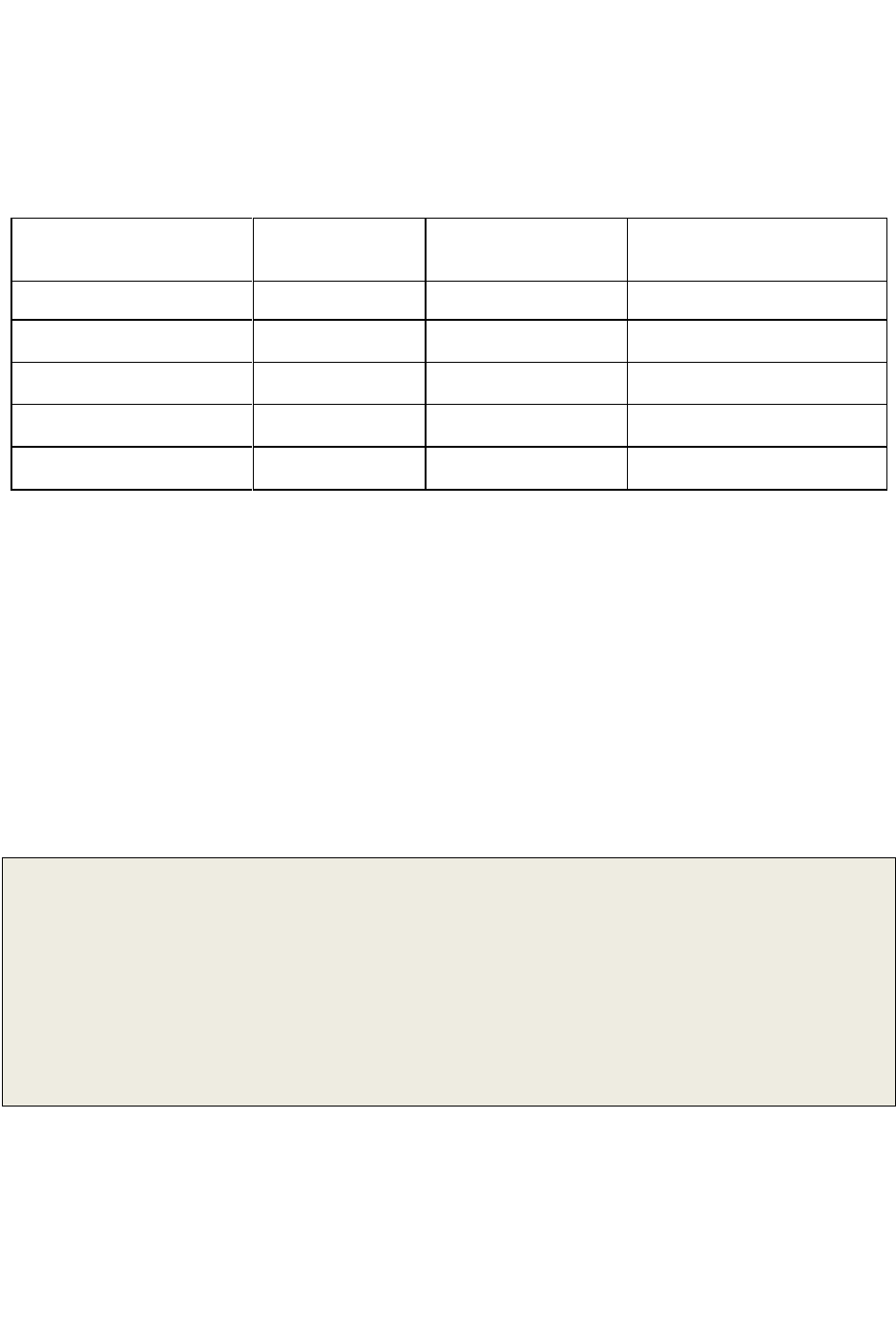
В исчислении высказываний вводится пять логических связок (табл. 3),

с помощью которых в соответствии с правилами построения составляются

логические формулы.

Таблица 3

Логические связки

Название

Обычное

обозначение

Тип

Другие обозначения

Отрицание



Унарный

-, ~, NOT, НЕ

Конъюнкция

Бинарный

& , ., AND , И *

Дизъюнкция



Бинарный

OR ИЛИ

Импликация



Бинарный

=> ->

Эквивалентность



Бинарный

<=> <-> ~

* Примечание: не путать со значением истинности И.

Совокупность правил построения логических формул на основе

высказываний включает три компонента:

− базис: всякое высказывание является формулой;

− индукционный шаг: если X и Y - формулы, то X, (X ^ Y), (X  Y), X

Y и X  Y – формулы;

− ограничение: формула однозначно получается с помощью правил,

описанных в базисе и индукционном шаге.

Формулы обозначаются прописными буквами латинского алфавита с

индексами. Образцы логических формул приведены в примере.

Примеры

а) T = S1 ^ S2;

б) N = H1H2.

Выражение а) можно прочитать так: «Логическая формула T есть

конъюнкция (логическая связка И) логических высказываний S1 и S2».

Интерпретация же выражения б) следующая: «Логическая формула N

есть дизъюнкция (логическая связка ИЛИ) отрицания (НЕ) логического

высказывания H1 и логического высказывания H2».

Значение истинности логической формулы является функцией значений

истинности составляющих ее высказываний и может быть определено

однозначно с помощью таблиц истинности. Ниже приводятся таблицы

истинности для отрицания и бинарных связок (табл. 4, 5)

Таким образом, если известны значения истинности для высказываний

из примера а), например S1 = И, S2 = Л, то значение истинности для формулы

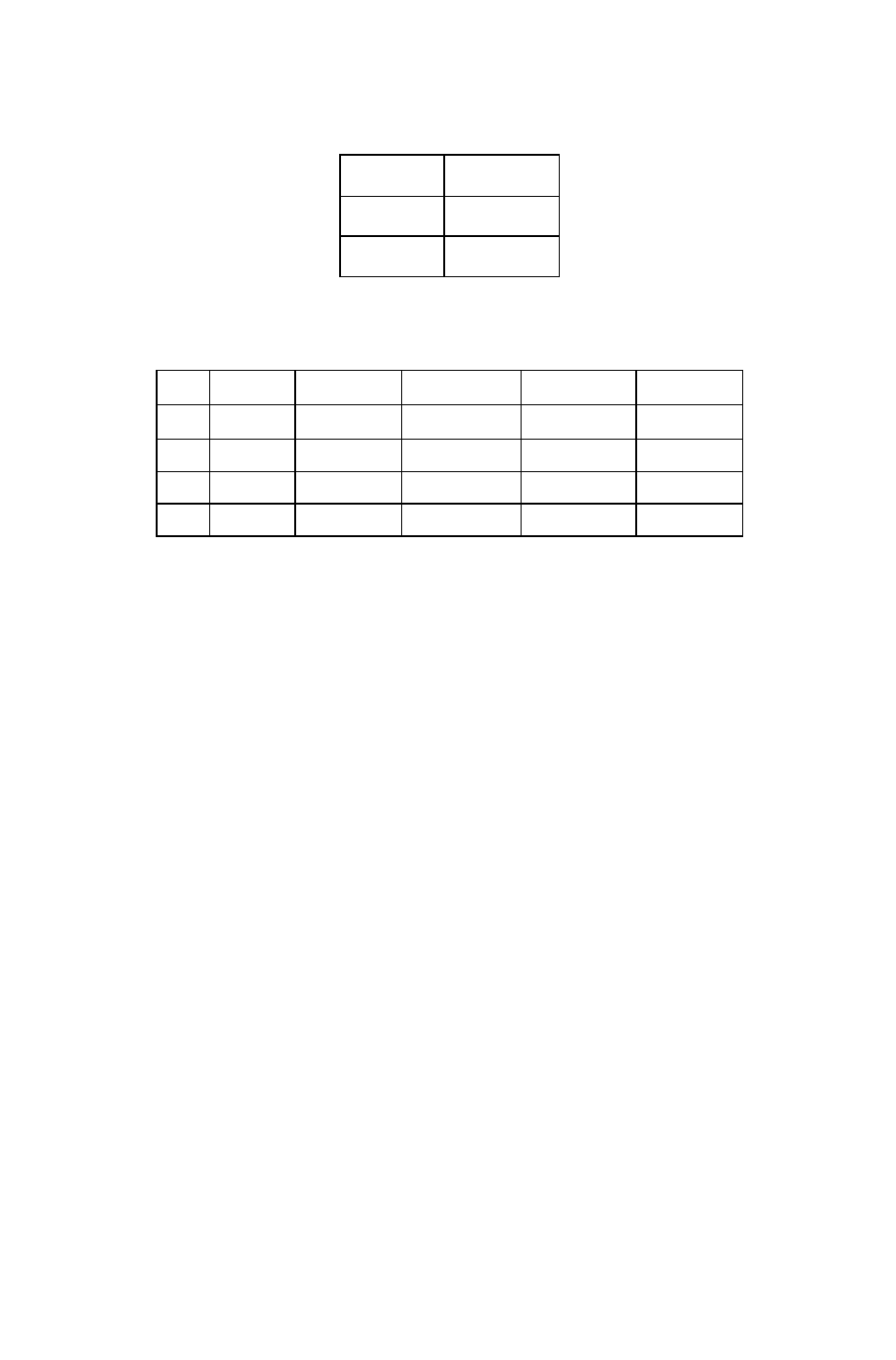
- 43 -

T можно найти на пересечении второй строки и третьего столбца в табл.5, то

есть T = Л.

Таблица 4

Таблица истинности для отрицания

¬X

Таблица 5

Таблица истинности для бинарных связок

X ^ Y

X Y

XY

X  Y

Логика предикатов первого порядка

Отношения между объектами описываются с помощью специальных

математических понятий, названных логическими предикатами, а исчисление

предикатов - это раздел логики, который занимается их изучением.

Любая логика есть формальная система, для которой должны быть

определены:

− алфавит системы — счетное множество символов;

− формулы системы — некоторое подмножество всех слов, которые

можно образовать из символов, входящих в алфавит (обычно задается

процедура, позволяющая составлять формулы из символов алфавита

системы);

− аксиомы системы — выделенное множество формул системы;

− правила вывода системы — конечное множество отношений между

формулами системы.

Словарь исчисления предикатов в стандартном изложении включает

следующие понятия:

− переменные (будем обозначать их последними буквами английского

алфавита u, v, x, y, z);

− константы (будем обозначать их первыми буквами английского

алфавита a, b, c, d):

o индивидные константы;

o функциональные константы;

o предикатные константы;

− высказывания;

- 44 -

− логические связки(¬ (отрицание), конъюнкция, дизъюнкция,

импликация);

− кванторы: (существования, всеобщности);

− термы;

− функциональные формы;

− предикатные формы;

− атомы;

− формулы.

Индивидные константы и индивидные переменные

Они подобны константам и переменным из математического анализа, с

той лишь разницей, что область их изменения представляет собой индивиды, а

не действительные числа. В теории искусственного интеллекта именованные

константы и переменные в памяти агента, соответствующие объектам и

понятием в реальном мире принято называть концептами. В языках первого

порядка, переменные бывают только индивидные, поэтому их называют

просто переменные. Как будет показано далее, применение языков первого

порядка и отказ от использования языков высокого порядка накладывает

дополнительные ограничения на класс рассматриваемых предложений

естественного языка. Индивидные константы будут обозначаться строчными

буквами a, b, c, u, v, w латинского алфавита с индексами или мнемоническими

именами, взятыми из текста. Для обозначения переменных будут

использоваться строчные буквы x,y,z, латинского алфавита с индексами.

Пример.

Индивидные константы: a1, b1, c, u, v1, продавец_w, k22, покупка_l,

m10, книга_a1 .

Переменные: x, y2, z33.

Предикатные константы

Предикатные константы служат обозначением отношения, которое

описывает предикат. Предикатная константа не меняет своего значения

истинности. Она связана с подходящим числом аргументов или параметров,

называемых термами, образуя предикатную форму. Обозначением

предикатной константы служат мнемонические имена или буква латинского

алфавита Р с индексами. В языке предикатов содержится язык высказываний,

так как высказывание - не что иное, как предикатная константа без

аргументов, или нуль-местная предикатная форма. Семантическая область

предикатной формы совпадает с областью изменения высказывания, т.е.

{И,Л}.

Функциональные константы

Функциональная константа (f, g, h) так же как предикатная константа,

соединяясь с подходящим числом термов, образует функциональную форму.

Отличие функциональной формы от предикатной формы заключается в том,

- 45 -

что ее семантическую область составляет множество индивидных констант.

Нуль-местная функциональная константа - просто индивидная константа.

логические связки в исчислении предикатов служат для образования формул.

Кванторы. В исчислении предикатов используются два квантора:

квантор общности () и квантор существования ().

Выражение xP читается как «для всякого х P истинно».

Выражение xP читается как «существует такой x, для которого P

истинно».

Термом называется выражение, образованное из переменных и

констант, возможно, с применением функций.

Термы, формы, атомы и формулы в исчислении предикатов строятся

с помощью нижеследующих правил:

− всякая переменная или константа есть терм;

− если t1,...,tn — термы, а f — n-местный функциональный символ, то

f(t1,...,tn) — терм;

− других термов нет.

По сути дела, все объекты в логике предикатов первого порядка

представляются именно в виде термов.

Если терм не содержит переменных, то он называется основным или

константным термом.

Термом (t1,t2 ...tn) является всякая переменная и всякая

функциональная форма.

Функциональная форма – это функциональная константа,

соединенная с подходящим числом термов. Если f - функциональная n-

местная константа и t1 ..., tn - термы, то соответствующая форма обычно

обозначается через f(t1, ...,tn). Если n=0, то пишется просто f.

Предикатная форма – это предикатная константа, соединенная с

подходящим числом термов. Если p соответствующая m -местная константа и

t1, ..., tn - термы, то соответствующая форма обозначается через p(t1,...,tm).

Атом – это предикатная форма или некоторое равенство, т.е.

выражение типа (s=t), где s и t - термы.

Атомная или элементарная формула получается путѐм применения

предиката к термам, точнее, это выражение p(t1,...,tn), где p — n-местный

предикатный символ (формула), а t1,...,tn — термы.

Понятие формулы определяется рекурсивно (индуктивно)

следующими правилами:

- атом есть формула;

- если A - формула , A -формула;

- если A и B - формулы, то (A ^ B), (A  B), (A  B) и (A  B) формулы;

- если A - формула и x - переменная, то xA и xA - формулы.

Представим алфавит логики предикатов через понятия.

Константы. Они служат именами индивидуумов (в отличие от имен

совокупностей): объектов, людей или событий. Константы представляются

- 46 -

символами вроде Жак_2 (добавление 2 к слову Жак указывает на вполне

определенного человека среди людей с таким именем), Книга_22, Посылка_8.

Переменные. Обозначают имена совокупностей, таких как человек,

книга, посылка, событие. Символ Книга_22 представляет вполне

определенный экземпляр, а символ книга указывает либо множество «всех

книг», либо «понятие книги». Символами x, y, z представлены имена

совокупностей (определенных множеств или понятий).

Предикатные имена (предикатные константы). Они задают правила

соединения констант и переменных, например правила грамматики,

процедуры, математические операции. Для предикативных имен

используются символы наподобие следующих фраз: Посылать, Писать, Плюс,

Разделить.

Функциональные имена (функциональные константы) представляют

такие же правила, как и предикаты. Чтобы не спутать с предикатными

именами, функциональные имена пишут одними строчными буквами: фраза,

посылать, писать, плюс, разделить.

Символы, которые применяются для представления констант,

переменных, предикатов и функций, не являются «словами русского языка».

Они суть символы некоторого представления - слова «объектного языка» (в

нашем случае языка предикатов).

Представление должно исключать всякую двусмысленность языка.

Поэтому имена индивидуумов содержат цифры, приписываемые к именам

совокупностей. Жак_1 и Жак_2 представляют двух людей с одинаковыми

именами. Эти представления суть конкретизации имени совокупности «Жак».

Предикат – это предикатное имя вместе с подходящим числом термов.

Предикат называют также предикатной формой.

Пример. По-русски: Жак посылает книгу Мари, логически: Посылка

(Жак_2, Мари_4, Книга_22).

Нечѐткая логика

Появление нечетких логик, теории нечетких множеств и других

«нечетких» теорий связано с работой американского ученого Заде. Основная

идея Заде состояла в том, что человеческий способ рассуждений,

опирающийся на естественный язык, не может быть описан в рамках

традиционных математических формализмов. Этим формализмам присуща

строгая однозначность интерпретации, а все, что связано с использованием

естественного языка, имеет многозначную интерпретацию. Цель Заде

состояла в построении новой математической дисциплины, в основе которой

лежала бы не классическая теория множеств, а теория нечетких множеств.

Последовательно проводя идею нечеткости, по мнению Заде, можно

построить нечеткие аналогии всех основных математических понятий и

создать необходимый формальный аппарат для моделирования человеческих

рассуждений и человеческого способа решения задач (рис. 17).

- 47 -

Создание теории нечетких множеств

- Решение

Математическая теория нечетких множеств

- Основа механизма

Формализация человеческого способа

рассуждений

- Задача

Тезис – человек в своей повседневной жизни

мыслит и принимает решения на основе нечетких

понятий

- Проблема

В настоящее время теория нечѐтких множеств и нечѐткой логики (fuzzy

set & fuzzy logic) занимает прочное место среди ведущих направлений

искусственного интеллекта. Понятие «нечѐткости», примененное изначально

к множествам, а затем в логике, было успешно распространено в другие

области математики и информатики и сейчас уже существуют:

- теория нечетких отношений;

- теория нечетких множеств;

- теория нечетких мер и интегралов;

- теория нечетких чисел и уравнений:

- теория нечеткой логики и приближенных рассуждений:

- теория нечетких языков;

- теория нечетких алгоритмов;

- теория нечетких моделей оптимизации и принятия решений.

Наиболее популярны у российских заказчиков следующие пакеты :

1) CubiCalc 2.0 RTC – одна из наиболее мощных коммерческих

экспертных систем на основе нечеткой логики, позволяющая

создавать собственные прикладные экспертные системы;

2) CubiQuick – академическая версия пакета CubiCalc;

3) RuleMaker – программа автоматического извлечения нечетких

правил из входных данных;

4) FuziCalc – электронная таблица с нечеткими полями,

позволяющая делать быстрые оценки при неточно известных

данных без накопления ошибки;

5) OWL – пакет, содержащий исходные тексты всех известных видов

нейронных сетей, нечеткой ассоциативной памяти и т.д.

Основными «потребителями» нечѐткой логики на рынке России

являются: банкиры, финансисты и специалисты в области политического и

экономического анализа.

Рис. 17. Логика возникновения теории нечѐтких множеств

- 48 -

В большинстве решаемых человеком задач не требуется высокая

точность. Часто приходится находить разумный компромисс между

понятиями «точность» и «важность» при общении с реальным миром.

Например: для принятия решения о переходе улицы человек не оценивает

скорость приближающегося автомобиля с точностью до десятых долей метров

в секунду. Он определяет для себя скорость автомобиля как «очень быструю»,

«быструю», «медленную» и т.д., т.е. использует для обозначения скорости

лингвистические переменные.

В теории нечѐтких множеств предлагаются следующие способы

формализации нечѐтких понятий.

Первый способ (основан на работах Заде) предполагает отказ от

основного утверждения классической теории множеств о том, что некоторый

элемент может либо принадлежать, либо не принадлежать множеству. При

этом вводится специальная характеристическая функция множества - так

называемая функция принадлежности, которая принимает значения из

интервала [0,1]. Этот способ приводит к континуальной логике.

При втором более общем способе формализации нечеткости

предполагается, что характеристические функции множества принимают

значение не из интервала [0,1], а в конечной или бесконечной дистрибутивной

решетке. Это обобщение называется нечеткими множествами в смысле

Гогена.

Третий способ – P-нечеткие множества. При этом обобщении каждый

элемент универсального множества связан не с точкой в интервале [0,1], а с

подмножеством или частью этого интервала. Алгебра P-нечетких множеств

может быть сведена к алгебре классов.

Четвертый способ – гетерогенные нечеткие множества. Здесь в общем

случае элементам универсального множества ставятся в соответствие

значения в различных дистрибутивных решетках. Каждый элемент может

быть связан с наиболее подходящей к нему оценкой. Более того, сами

значения оценок могут быть нечеткими и задаваться в виде функций.

Общее представление о нечѐткой логике получено. Теперь обо всѐм

подробней. Рассмотрим понятийный аппарат, в основе которого лежит

понятие «лингвистической переменной».

Определение лингвистической переменной (интуитивное)

Если переменная может принимать значения слов в естественном языке

(например, «маленький», «быстрый» и т.п.), то эта переменная определяется

как лингвистическая переменная.

Слова, значения которых принимает лингвистическая переменная,

обычно обозначают собой нечѐткие множества.

Интеллектуальные информационные системы: Методические указания к лабораторному практикуму по

курсу "Интеллектуальные информационные системы" для студентов специальности 071900 -Информационные

системы в экономике / Уфимск. гос. авиац. техн. ун-т; сост.: Г.Г.Куликов, Т.В.Брейкин, Л.З.Камалова. - Уфа,

1999. -40 с.

- 49 -

Лингвистическая переменная может принимать своими значениями

либо слова, либо числа.

Определение лингвистической переменной (формальное)

Лингвистической переменной называется пятерка (х, Т(х), Х, G, M),

где х – имя переменной;

Т(х) – множество имен лингвистических значений переменной х,

каждое из которых является нечетким множеством на множестве Х;

G – синтаксическое правило для образования имен значений х;

М – семантическое правило для ассоциирования каждой величины

значения с ее понятием.

Цель концепции лингвистической переменной состоит в том, чтобы

формальным образом сказать, что переменная может принимать в качестве

значений слова из естественного языка.

Другим словами, каждая лингвистическая переменная состоит из:

− названия;

− множества своих значений, которое также называется базовым терм-

множеством T. Элементы базового терм-множества представляют

собой названия нечетких переменных;

− универсального множества X;

− синтаксического правила G, по которому генерируются новые термы с

применением слов естественного или формального языка;

− семантического правила P, которое каждому значению

лингвистической переменной ставит в соответствие нечеткое

подмножество множества X.

Например, если мы говорим «быстрая скорость», то переменная

«скорость» должна пониматься как лингвистическая переменная, но это не

означает, что переменная «скорость» не может принимать реальные значения

Нечѐткая переменная описывается набором (N,X,A),

где N – это название переменной, X – универсальное множество

(область рассуждений), A – нечѐткое множество на X.

Значениями лингвистической переменной могут быть нечѐткие

переменные, т.е. лингвистическая переменная находится на более высоком

уровне, чем нечѐткая переменная.

Основной подход к формализации нечѐткости состоит в следующем.

Нечѐткое множество образуется путем введения обобщенного понятия

принадлежности, т.е. расширения двухэлементного множества значений

характеристической функции {0,1} до континуума [0,1]. Это означает, что

переход от полной принадлежности объекта классу к полной его

непринадлежности происходит не скачком, а плавно, постепенно, причѐм

принадлежность элемента множеству выражается числом из интервала [0,1].

- 50 -

Нечёткое множество (НМ)

, определяется математически как совокупность

упорядоченных пар, составленных из элементов x универсального множества

X и соответствующих степеней принадлежности μа(x) или (поскольку

функция принадлежности является исчерпывающей характеристикой НМ)

непосредственно в виде функции

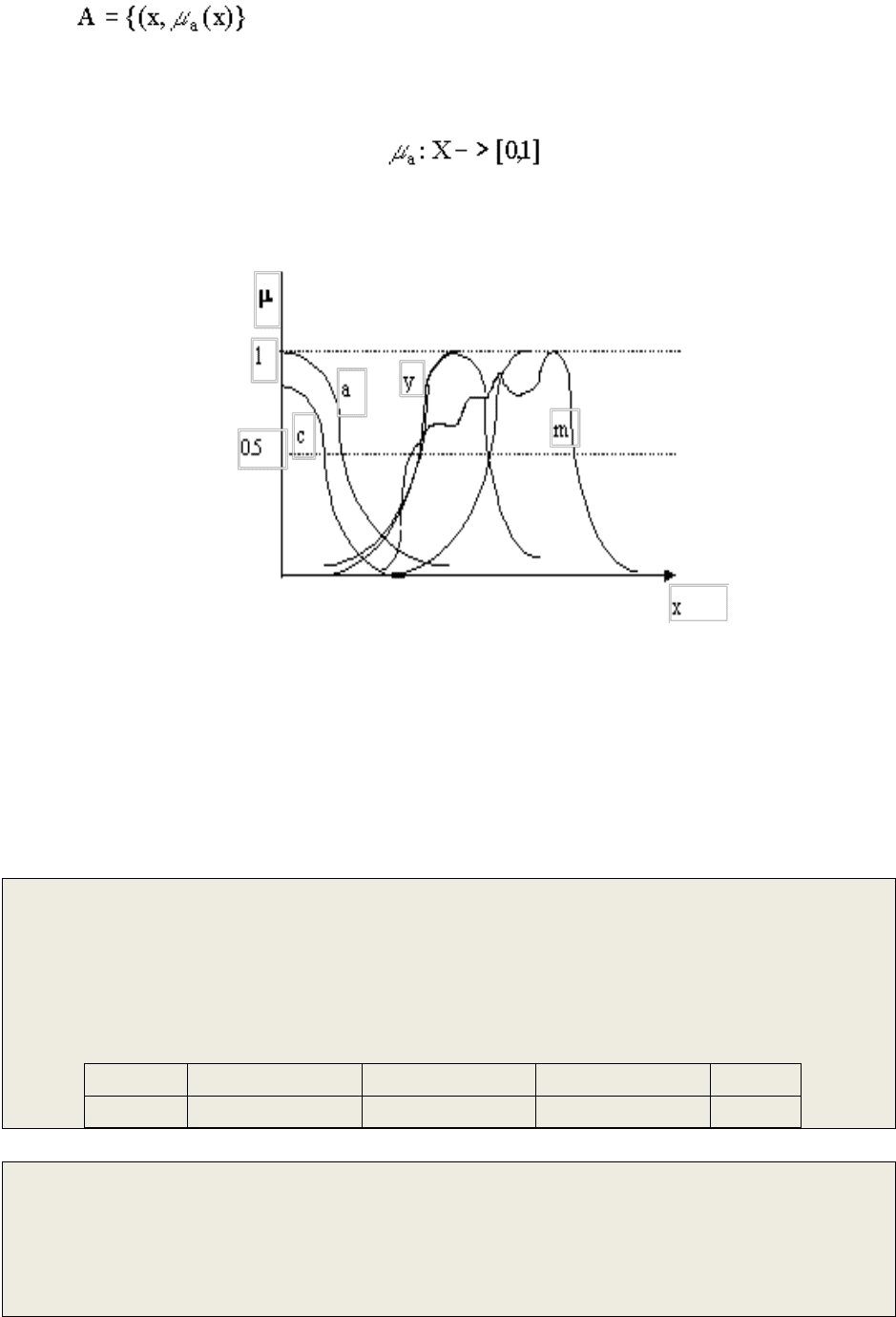
Универсальным множеством X нечѐткого множества A называется

область определения функции принадлежности μа. На рис. 18 представлены

основные разновидности функций принадлежности.

Рис. 18. Вид функций принадлежности

По виду функций принадлежности их различают на :

− субмодальные (Рис 1. c);

− амодальные(Рис 1. a);

− многомодальные(Рис 1. m);

− унимодальные (Рис 1. u).

−

Пример.

1) A ={(x1,0.2),(x2,0.6),(x3,1),(x4,0.8)};

2) A = 0.2|x1 + 0.6|x2 + 1|x3 + 0.8|x4.

3) Этот же пример можно представить в виде таблицы.

Таблица 6

Таблица описания функции принадлежности

х4

A =

0.2

0.6

0.8

Пример «Множество высоких людей»

В реальной жизни такое понятие, как «рост высокого человека»,

является субъективным. Одни считают, что высокий человек должен быть

ростом более 170 см, другие - более 180 см, третьи - более 190 см. Нечѐткие

множества позволяют учесть такую размытость оценок.