Маслова Т.Н., Суходский А.М. Справочник школьника по математике. 5-11 кл
Подождите немного. Документ загружается.


ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
167166
á) Ðàññóæäàÿ àíàëîãè÷íî, ïîëó÷àåì
=)2/1(arcsin
.6/p=
Íî
,)2/1(arcsin)2/1(arcsin -=-
çíà÷èò,
.6/)2/1(arcsin p-=-
â) Ïî îïðåäåëåíèþ,
)2/2(arccos=a
ýòî òà-
êîå ÷èñëî, ÷òî
2/2cos =a
è
.0 p£a£
Îòñþäà ñëå-
äóåò, ÷òî
,4/p=a
ò. å.
.4/)2/2(arccos p=
ã) Òàê êàê
,arccos)(arccos aa -p=-
òî ïîëó÷àåì
.4/34/)2/2(arccos)2/2(arccos p=p-p=-p=-
ä) Ïî îïðåäåëåíèþ,
3arctg=a
ýòî òàêîå ÷èñ-
ëî, ÷òî
3tg =a
è
.2/2/ p<a<p-
Îòñþäà ñëåäóåò,
÷òî
,3/p=a
ò. å.
.3/3arctg p=
å) Ðàññóæäàÿ àíàëîãè÷íî, ïîëó÷àåì
.4/1arctg p=
Íî
,1arctg)1(arctg -=-
çíà÷èò,
.4/)1(arctg p-=-
æ) Ïî îïðåäåëåíèþ,
0arcctg=a
ýòî òàêîå ÷èñ-
ëî, ÷òî
0ctg =a
è
.0 p<a<
Îòñþäà ñëåäóåò, ÷òî
,2/p=a
ò. å.
.2/0arcctg p=
ç) Ðàññóæäàÿ àíàëîãè÷íî, íàõîäèì
=3arcctg
.6/p=
Òàê êàê
,arcctg)(arcctg aa -p=-
òî
.6/56/3arcctg)3(arcctg p=p-p=-p=-
n
àðêñèíóñîì ÷èñëà
]1,1[-Îa
íàçûâàåòñÿ òàêîå
÷èñëî
],2/,2/[ pp-Îa
ñèíóñ êîòîðîãî ðàâåí à:
,arcsin a=a
åñëè
a=asin
è
;2/2/ p£a£p-
àðêêîñèíóñîì ÷èñëà
]1,1[-Îa
íàçûâàåòñÿ òà-
êîå ÷èñëî
,],0[ pÎa
êîñèíóñ êîòîðîãî ðàâåí à:
,arccos
a=a
åñëè
a=acos
è
;0 p£a£
àðêòàíãåíñîì ÷èñëà à íàçûâàåòñÿ òàêîå ÷èñëî
),2/,2/( pp-=a
òàíãåíñ êîòîðîãî ðàâåí à:
,arctg a=a
åñëè
a=atg
è
;2/2/ p<a<p-
àðêêîòàíãåíñîì ÷èñëà à íàçûâàåòñÿ òàêîå ÷èñ-
ëî
),,0( pÎa
êîòàíãåíñ êîòîðîãî ðàâåí à:
,arcctg a=a
åñëè
a=actg
è
.0 p<a<
Ñïðàâåäëèâû ñëåäóþùèå òîæäåñòâà:
,arcsin)(arcsin aa -=-
,arccos)(arccos aa -p=-
,arctg)(arctg aa -=-
.arcctg)(arcctg aa -p=-
Ï ð è ì å ð. Âû÷èñëèòü:
à)
);2/3(arcsin
ä)
;3arcctg
á)
);2/1(arcsin -
å)
);1(arctg -
â)
);2/2(arccos
æ)
;0arcctg
ã)
;)2/2(arccos -
ç)
).3(arcctg -
q à) Ïî îïðåäåëåíèþ,
)2/3(arcsin=a
ýòî
òàêîå ÷èñëî, ÷òî
2/3sin =a
è
.2/2/ p£a£p-
Îò-
ñþäà ñëåäóåò, ÷òî
,3/p=a
ò. å.
.3/)2/3(arcsin p=
Î

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
167166
á) Ðàññóæäàÿ àíàëîãè÷íî, ïîëó÷àåì
=)2/1(arcsin
.6/p=
Íî
,)2/1(arcsin)2/1(arcsin -=-
çíà÷èò,
.6/)2/1(arcsin p-=-
â) Ïî îïðåäåëåíèþ,
)2/2(arccos=a
ýòî òà-
êîå ÷èñëî, ÷òî
2/2cos =a
è
.0 p£a£
Îòñþäà ñëå-
äóåò, ÷òî
,4/p=a
ò. å.
.4/)2/2(arccos p=
ã) Òàê êàê
,arccos)(arccos aa -p=-
òî ïîëó÷àåì
.4/34/)2/2(arccos)2/2(arccos p=p-p=-p=-
ä) Ïî îïðåäåëåíèþ,
3arctg=a
ýòî òàêîå ÷èñ-
ëî, ÷òî
3tg =a
è
.2/2/ p<a<p-
Îòñþäà ñëåäóåò,
÷òî
,3/p=a
ò. å.
.3/3arctg p=
å) Ðàññóæäàÿ àíàëîãè÷íî, ïîëó÷àåì
.4/1arctg p=
Íî
,1arctg)1(arctg -=-
çíà÷èò,
.4/)1(arctg p-=-
æ) Ïî îïðåäåëåíèþ,
0arcctg=a
ýòî òàêîå ÷èñ-
ëî, ÷òî
0ctg =a
è
.0 p<a<
Îòñþäà ñëåäóåò, ÷òî
,2/p=a
ò. å.
.2/0arcctg p=
ç) Ðàññóæäàÿ àíàëîãè÷íî, íàõîäèì
=3arcctg
.6/p=
Òàê êàê
,arcctg)(arcctg aa -p=-
òî
.6/56/3arcctg)3(arcctg p=p-p=-p=-
n
àðêñèíóñîì ÷èñëà
]1,1[-Îa
íàçûâàåòñÿ òàêîå
÷èñëî
],2/,2/[ pp-Îa
ñèíóñ êîòîðîãî ðàâåí à:
,arcsin a=a
åñëè
a=asin
è
;2/2/ p£a£p-
àðêêîñèíóñîì ÷èñëà
]1,1[-Îa
íàçûâàåòñÿ òà-
êîå ÷èñëî
,],0[ pÎa
êîñèíóñ êîòîðîãî ðàâåí à:
,arccos
a=a
åñëè
a=acos
è
;0 p£a£
àðêòàíãåíñîì ÷èñëà à íàçûâàåòñÿ òàêîå ÷èñëî
),2/,2/( pp-=a
òàíãåíñ êîòîðîãî ðàâåí à:
,arctg a=a
åñëè
a=atg
è
;2/2/ p<a<p-
àðêêîòàíãåíñîì ÷èñëà à íàçûâàåòñÿ òàêîå ÷èñ-
ëî
),,0( pÎa
êîòàíãåíñ êîòîðîãî ðàâåí à:
,arcctg a=a
åñëè
a=actg
è
.0 p<a<
Ñïðàâåäëèâû ñëåäóþùèå òîæäåñòâà:
,arcsin)(arcsin aa -=-
,arccos)(arccos aa -p=-
,arctg)(arctg aa -=-
.arcctg)(arcctg aa -p=-
Ï ð è ì å ð. Âû÷èñëèòü:
à)
);2/3(arcsin
ä)
;3arcctg
á)
);2/1(arcsin -
å)
);1(arctg -
â)
);2/2(arccos
æ)
;0arcctg
ã)
;)2/2(arccos -
ç)
).3(arcctg -
q à) Ïî îïðåäåëåíèþ,
)2/3(arcsin=a
ýòî
òàêîå ÷èñëî, ÷òî
2/3sin =a
è
.2/2/ p£a£p-
Îò-
ñþäà ñëåäóåò, ÷òî
,3/p=a
ò. å.
.3/)2/3(arcsin p=
Î
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
169168
Çàäà÷à II. Ïîñòðîèòü ãðàôèê ôóíêöèè
),(xfy -=
çíàÿ ãðàôèê ôóíêöèè
).(xfy =
q Ïðè îäíîì è òîì æå çíà÷åíèè õ îðäèíàòû
òî÷åê ãðàôèêîâ ôóíêöèé
)(xfy =
è
)(xfy -=
îòëè-
÷àþòñÿ òîëüêî çíàêàìè. Çíà÷èò, ãðàôèê ôóíêöèè
)(xfy -=
ìîæíî ïîëó÷èòü èç ãðàôèêà
)(xfy =
ïðå-
îáðàçîâàíèåì ñèììåòðèè ïîñëåäíåãî îòíîñè-
òåëüíî îñè Îõ. n
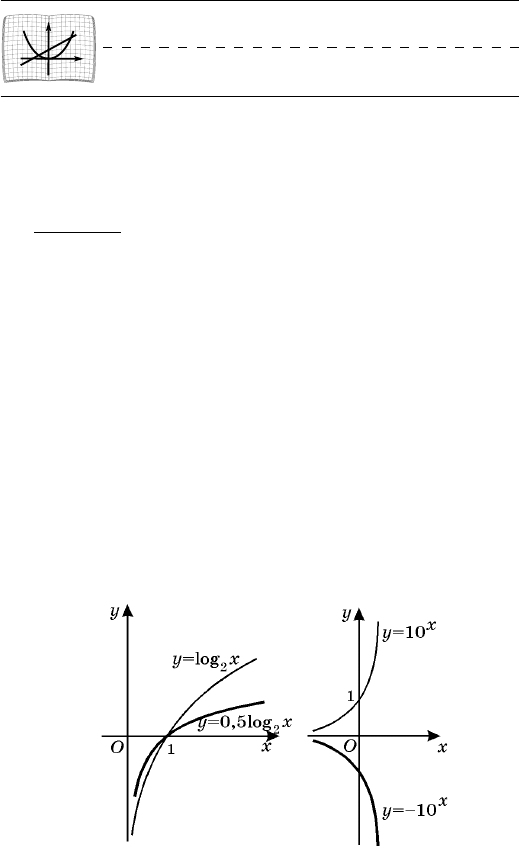
Íà ðèñ. 57 èçîáðàæåíû ãðàôèêè ôóíêöèé ó =
= 10
õ
è ó = 10
õ
.
Çàäà÷à III. Ïîñòðîèòü ãðàôèê ôóíêöèè
),(xmfy =
ãäå
,1,0 -¹< mm
çíàÿ ãðàôèê ôóíêöèè
).(xfy =
q Òàê êàê
)
,
(
)
(
xfmxmf -=
òî ãðàôèê ôóíêöèè
)(xmfy =
ìîæíî ïîëó÷èòü ðàñòÿæåíèåì (ñæàòèåì)
ãðàôèêà ôóíêöèè
)(xfy =
îò îñè Îõ ñ êîýôôèöèåíòîì
m
è ïîñëåäóþùèì ïðåîá-
ðàçîâàíèåì ñèììåòðèè îò-
íîñèòåëüíî îñè Îõ (ñì. çà-
äà÷è I è II). n
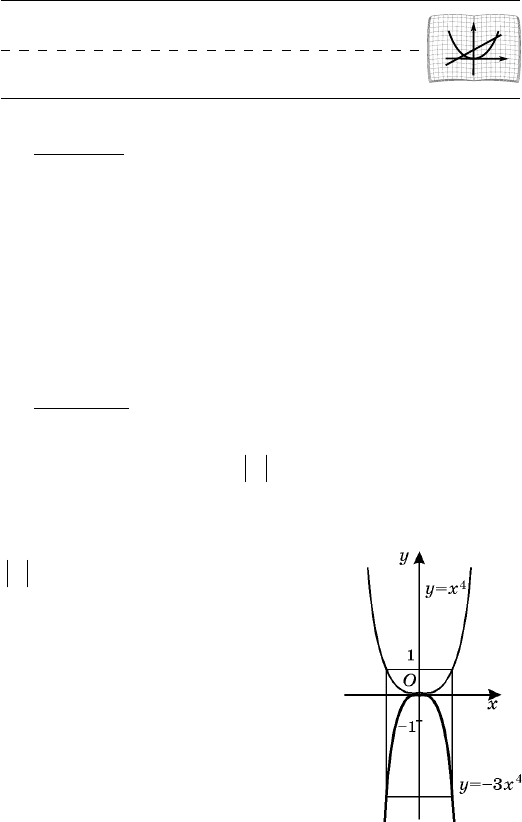
Íà ðèñ. 58 èçîáðàæåíû
ãðàôèêè ôóíêöèé ó = õ
4
è
ó = 3õ
4
.
131. Ãðàôèêè ôóíêöèé ó =
= àõ
2
, ó = àõ
3
. Ãðàôèêîì
ôóíêöèè ó = õ
2
ÿâëÿåòñÿ ïà-
ðàáîëà. ×òîáû ïîñòðîèòü ãðà-
ôèê ôóíêöèè ó = àõ
2
, íóæíî
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
130. Ïîñòðîåíèå ãðàôèêà ôóíêöèè
mf(x).y =
Çàäà÷à I. Ïîñòðîèòü ãðàôèê ôóíêöèè
),(xmfy =
ãäå
,1,0 ¹> mm
çíàÿ ãðàôèê ôóíêöèè
).(xfy =
q Îðäèíàòû òî÷åê ãðàôèêà ôóíêöèè
)(xmfy =
ïî-
ëó÷àþòñÿ óìíîæåíèåì íà
m
ñîîòâåòñòâóþùèõ îðäè-
íàò òî÷åê ãðàôèêà ôóíêöèè
).(xfy =
Òàêîå ïðåîáðà-
çîâàíèå ãðàôèêà ôóíêöèè
)(xfy =
íàçûâàåòñÿ åãî
ðàñòÿæåíèåì îò îñè Îõ ñ êîýôôèöèåíòîì ò, åñëè
,1>m
è ñæàòèåì ê îñè Îõ, åñëè
.10 << m
n
Íà ðèñ. 56 èçîáðàæåíû ãðàôèêè ôóíêöèé
xy
2
log
=
è
.log5,0
2
xy =
Ðèñ. 57
Ðèñ. 56
Ðèñ. 58
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
169168
Çàäà÷à II. Ïîñòðîèòü ãðàôèê ôóíêöèè
),(xfy -=
çíàÿ ãðàôèê ôóíêöèè
).(xfy =
q Ïðè îäíîì è òîì æå çíà÷åíèè õ îðäèíàòû
òî÷åê ãðàôèêîâ ôóíêöèé
)(xfy =
è
)(xfy -=
îòëè-
÷àþòñÿ òîëüêî çíàêàìè. Çíà÷èò, ãðàôèê ôóíêöèè
)(xfy -=
ìîæíî ïîëó÷èòü èç ãðàôèêà
)(xfy =
ïðå-
îáðàçîâàíèåì ñèììåòðèè ïîñëåäíåãî îòíîñè-
òåëüíî îñè Îõ. n
Íà ðèñ. 57 èçîáðàæåíû ãðàôèêè ôóíêöèé ó =
= 10
õ
è ó = 10
õ
.
Çàäà÷à III. Ïîñòðîèòü ãðàôèê ôóíêöèè
),(xmfy =
ãäå
,1,0 -¹< mm
çíàÿ ãðàôèê ôóíêöèè
).(xfy =
q Òàê êàê
)
,
(
)
(
xfmxmf -=
òî ãðàôèê ôóíêöèè
)(xmfy =
ìîæíî ïîëó÷èòü ðàñòÿæåíèåì (ñæàòèåì)
ãðàôèêà ôóíêöèè
)(xfy =
îò îñè Îõ ñ êîýôôèöèåíòîì
m
è ïîñëåäóþùèì ïðåîá-
ðàçîâàíèåì ñèììåòðèè îò-
íîñèòåëüíî îñè Îõ (ñì. çà-
äà÷è I è II). n
Íà ðèñ. 58 èçîáðàæåíû
ãðàôèêè ôóíêöèé ó = õ
4
è
ó = 3õ
4
.
131. Ãðàôèêè ôóíêöèé ó =
= àõ
2
, ó = àõ
3
. Ãðàôèêîì
ôóíêöèè ó = õ
2
ÿâëÿåòñÿ ïà-
ðàáîëà. ×òîáû ïîñòðîèòü ãðà-
ôèê ôóíêöèè ó = àõ
2
, íóæíî
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
130. Ïîñòðîåíèå ãðàôèêà ôóíêöèè
mf(x).y =
Çàäà÷à I. Ïîñòðîèòü ãðàôèê ôóíêöèè
),(xmfy =
ãäå
,1,0 ¹> mm
çíàÿ ãðàôèê ôóíêöèè
).(xfy =
q Îðäèíàòû òî÷åê ãðàôèêà ôóíêöèè
)(xmfy =
ïî-
ëó÷àþòñÿ óìíîæåíèåì íà
m
ñîîòâåòñòâóþùèõ îðäè-
íàò òî÷åê ãðàôèêà ôóíêöèè
).(xfy =
Òàêîå ïðåîáðà-
çîâàíèå ãðàôèêà ôóíêöèè
)(xfy =
íàçûâàåòñÿ åãî
ðàñòÿæåíèåì îò îñè Îõ ñ êîýôôèöèåíòîì ò, åñëè
,1>m
è ñæàòèåì ê îñè Îõ, åñëè
.10 << m
n
Íà ðèñ. 56 èçîáðàæåíû ãðàôèêè ôóíêöèé
xy
2
log
=
è
.log5,0
2
xy =
Ðèñ. 57
Ðèñ. 56
Ðèñ. 58
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
171170
132. Ïîñòðîåíèå ãðàôèêà ôóíêöèè
+-= )( axfy
b.+
Äëÿ ïîñòðîåíèÿ ãðàôèêà ôóíêöèè
bxfy += )(
íàäî ïåðåíåñòè ãðàôèê ôóíêöèè
)(xfy =
íà âåêòîð
);0( b
âäîëü îñè îðäèíàò. Äàëåå, äëÿ ïîñòðîåíèÿ ãðà-
ôèêà ôóíêöèè
)( axfy -=
íàäî ïåðåíåñòè ãðàôèê
ôóíêöèè
)(xfy =
íà âåêòîð
)0;(a
âäîëü îñè àáñöèññ.
Íàêîíåö, äëÿ ïîñòðîåíèÿ ãðàôèêà ôóíêöèè
=y
baxf +-= )(
íàäî âûïîëíèòü ïàðàëëåëüíûé ïåðå-
íîñ ãðàôèêà ôóíêöèè y
)(xf=
è íà âåêòîð
),0;(a
è
íà âåêòîð
);0( b
, ò. å. â èòîãå íà âåêòîð (à; b).
Íà ïðàêòèêå ýòî ïðàâèëî óäîáíî èñïîëüçîâàòü â
ñëåäóþùåé ôîðìóëèðîâêå. ×òîáû ïîñòðîèòü ãðàôèê
ôóíêöèè
baxfy +-= )(
, íóæíî:
îñóùåñòâèòü ðàñòÿæåíèå (ñæàòèå) ïàðàáîëû ó = õ
2
îò
îñè Îõ ñ êîýôôèöèåíòîì
;a
ïðè ýòîì åñëè a < 0, òî
ãðàôèê ôóíêöèè
2
xay =
íóæíî åùå îòîáðàçèòü
ñèììåòðè÷íî îòíîñèòåëüíî îñè Îõ (ñì. ï. 130).
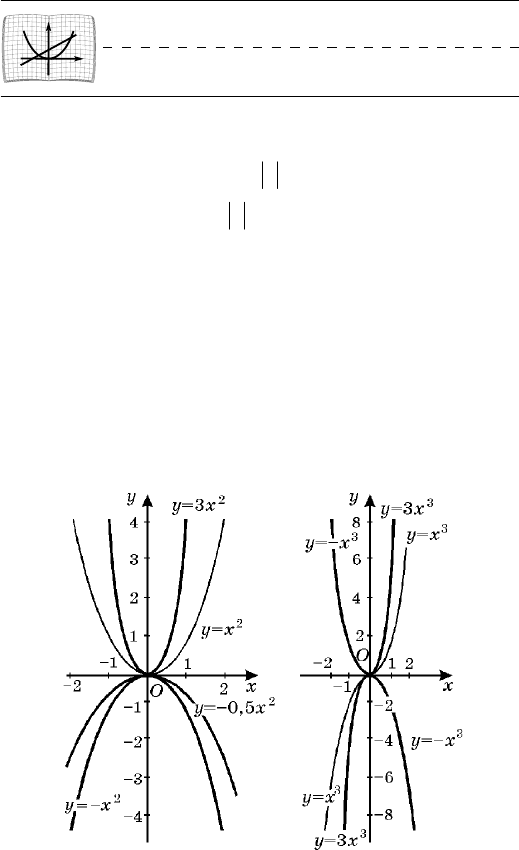
Íà ðèñ. 59 èçîáðàæåíû ãðàôèêè ôóíêöèè ó =
= àõ
2
äëÿ çíà÷åíèé à, ðàâíûõ 1; 1; 3; 0,5. Âñå ýòè
ãðàôèêè íàçûâàþò ïàðàáîëàìè. Ïðè à > 0 âåòâè
ïàðàáîëû, ñëóæàùåé ãðàôèêîì ôóíêöèè ó = àõ
2
, íà-
ïðàâëåíû ââåðõ, à ïðè a < 0 âíèç.
Àíàëîãè÷íî, çíàÿ ãðàôèê ôóíêöèè ó = õ
3
, ìîæíî
ïîñòðîèòü ãðàôèê ôóíêöèè âèäà ó = àõ
3
. Íà ðèñ. 60
èçîáðàæåíû ýòè ãðàôèêè äëÿ çíà÷åíèé à, ðàâíûõ 1;
1; 3.
Ðèñ. 60Ðèñ. 59 Ðèñ. 61 Ðèñ. 62
á)
à)
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
171170
132. Ïîñòðîåíèå ãðàôèêà ôóíêöèè
+-= )( axfy
b.+
Äëÿ ïîñòðîåíèÿ ãðàôèêà ôóíêöèè
bxfy += )(
íàäî ïåðåíåñòè ãðàôèê ôóíêöèè
)(xfy =
íà âåêòîð
);0( b
âäîëü îñè îðäèíàò. Äàëåå, äëÿ ïîñòðîåíèÿ ãðà-
ôèêà ôóíêöèè
)( axfy -=
íàäî ïåðåíåñòè ãðàôèê
ôóíêöèè
)(xfy =
íà âåêòîð
)0;(a
âäîëü îñè àáñöèññ.
Íàêîíåö, äëÿ ïîñòðîåíèÿ ãðàôèêà ôóíêöèè
=y
baxf +-= )(
íàäî âûïîëíèòü ïàðàëëåëüíûé ïåðå-
íîñ ãðàôèêà ôóíêöèè y
)(xf=
è íà âåêòîð
),0;(a
è
íà âåêòîð
);0( b
, ò. å. â èòîãå íà âåêòîð (à; b).
Íà ïðàêòèêå ýòî ïðàâèëî óäîáíî èñïîëüçîâàòü â
ñëåäóþùåé ôîðìóëèðîâêå. ×òîáû ïîñòðîèòü ãðàôèê
ôóíêöèè
baxfy +-= )(
, íóæíî:
îñóùåñòâèòü ðàñòÿæåíèå (ñæàòèå) ïàðàáîëû ó = õ
2
îò
îñè Îõ ñ êîýôôèöèåíòîì
;a
ïðè ýòîì åñëè a < 0, òî
ãðàôèê ôóíêöèè
2
xay =
íóæíî åùå îòîáðàçèòü
ñèììåòðè÷íî îòíîñèòåëüíî îñè Îõ (ñì. ï. 130).
Íà ðèñ. 59 èçîáðàæåíû ãðàôèêè ôóíêöèè ó =
= àõ
2
äëÿ çíà÷åíèé à, ðàâíûõ 1; 1; 3; 0,5. Âñå ýòè
ãðàôèêè íàçûâàþò ïàðàáîëàìè. Ïðè à > 0 âåòâè
ïàðàáîëû, ñëóæàùåé ãðàôèêîì ôóíêöèè ó = àõ
2
, íà-
ïðàâëåíû ââåðõ, à ïðè a < 0 âíèç.
Àíàëîãè÷íî, çíàÿ ãðàôèê ôóíêöèè ó = õ
3
, ìîæíî
ïîñòðîèòü ãðàôèê ôóíêöèè âèäà ó = àõ
3
. Íà ðèñ. 60
èçîáðàæåíû ýòè ãðàôèêè äëÿ çíà÷åíèé à, ðàâíûõ 1;
1; 3.
Ðèñ. 60Ðèñ. 59 Ðèñ. 61 Ðèñ. 62
á)
à)
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
173172
=+
÷
÷
ø
ö
ç
ç
è
æ
-
÷
÷
ø
ö
ç
ç
è
æ
+×+= c
a
b
a
b
x
a
b
xa
2
2
2
2
2
44
2
2
=+-
÷
ø
ö
ç
è
æ
+=+
÷
÷
ø
ö
ç
ç
è
æ
-
÷
ø
ö
ç
è
æ
+= c
a
b
a
b
xac
a
b
a
b
xa
42
4
2
2
2
2
2
2
.
4
4
2
2
2
a
bac
a
b
xa
-
+
÷
ø
ö
ç
è
æ
+=
Èòàê,
.
4
4
2
2
2
2
a
bac
a
b
xacbxaxy
-
+
÷
ø
ö
ç
è
æ
+=++=
(1)
1) âûïîëíèòü ïàðàëëåëüíûé ïåðåíîñ ïëîñêîñòè,
âûáðàâ â êà÷åñòâå íà÷àëà íîâîé ñèñòåìû êîîðäèíàò
yOx
¢¢¢
òî÷êó
O
¢
(à; b);
2) â ïëîñêîñòè
yOx
¢¢¢
ïîñòðîèòü ãðàôèê ôóíêöèè
).(xfy
¢
=
¢
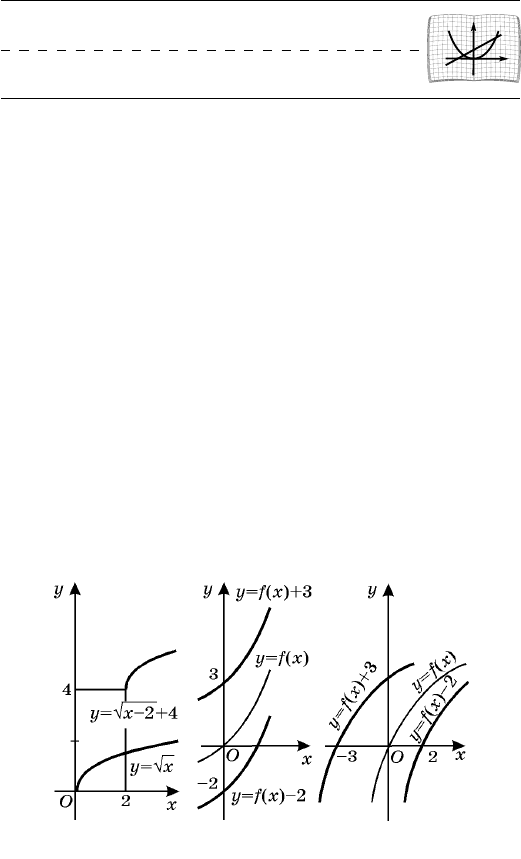
Ï ð è ì å ð. Ïîñòðîèòü ãðàôèê ôóíêöèè
.42 +-= xy
q 1) Âûïîëíèì ïàðàëëåëüíûé ïåðåíîñ ïëîñêîñòè,
ïîìåñòèâ íà÷àëî íîâîé ñèñòåìû êîîðäèíàò
yOx
¢¢¢
â
òî÷êó
O
¢
(2; 4).
2) Â ïëîñêîñòè
yOx
¢¢¢
ïîñòðîèì ãðàôèê ôóíêöèè
.xy
¢
=
¢
Ýòî è åñòü òðåáóåìûé ãðàôèê (ðèñ. 61).n
Íà ðèñ. 62, à èçîáðàæåíû ãðàôèêè ôóíêöèé
=y
),(xf= ,3)(,2)( +=-= xfyxfy
à íà ðèñ. 62, á ãðà-
ôèêè ôóíêöèé
)(xfy =
,
).3(),2( +=-= xfyxfy
133. Ãðàôèê êâàäðàòè÷íîé ôóíêöèè. Êâàäðà-
òè÷íîé íàçûâàþò ôóíêöèþ, êîòîðóþ ìîæíî çàäàòü
ôîðìóëîé âèäà
,
2
cbxaxy ++=
ãäå
cba ,,
ëþ-
áûå äåéñòâèòåëüíûå ÷èñëà, ïðè÷åì
.0
¹a
Äëÿ ïî-
ñòðîåíèÿ ãðàôèêà ýòîé ôóíêöèè âûïîëíèì ñëåäóþ-
ùèå ïðåîáðàçîâàíèÿ (íàçûâàåìûå âûäåëåíèåì ïîë-
íîãî êâàäðàòà) êâàäðàòíîãî òðåõ÷ëåíà
:
2
cbxax ++
=+
÷
ø
ö
ç
è
æ
+=++ cx
a
b
xacbxax
22
á)à)
Ðèñ. 63
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
173172
=+
÷
÷
ø
ö
ç
ç
è
æ
-
÷
÷
ø
ö
ç
ç
è
æ
+×+= c
a
b
a
b
x
a
b
xa
2
2
2
2
2
44
2
2
=+-
÷
ø
ö
ç
è
æ
+=+
÷
÷
ø
ö
ç
ç
è
æ
-
÷
ø
ö
ç
è
æ
+= c
a
b
a
b
xac
a
b
a
b
xa
42
4
2
2
2
2
2
2
.
4
4
2
2
2
a
bac
a
b
xa
-
+
÷
ø
ö
ç
è
æ
+=
Èòàê,
.
4
4
2
2
2
2
a
bac
a
b
xacbxaxy
-
+
÷
ø
ö
ç
è
æ
+=++=
(1)
1) âûïîëíèòü ïàðàëëåëüíûé ïåðåíîñ ïëîñêîñòè,
âûáðàâ â êà÷åñòâå íà÷àëà íîâîé ñèñòåìû êîîðäèíàò
yOx
¢¢¢
òî÷êó
O
¢
(à; b);
2) â ïëîñêîñòè
yOx
¢¢¢
ïîñòðîèòü ãðàôèê ôóíêöèè
).(xfy
¢
=
¢
Ï ð è ì å ð. Ïîñòðîèòü ãðàôèê ôóíêöèè
.42 +-= xy
q 1) Âûïîëíèì ïàðàëëåëüíûé ïåðåíîñ ïëîñêîñòè,
ïîìåñòèâ íà÷àëî íîâîé ñèñòåìû êîîðäèíàò
yOx
¢¢¢
â
òî÷êó
O
¢
(2; 4).
2) Â ïëîñêîñòè
yOx
¢¢¢
ïîñòðîèì ãðàôèê ôóíêöèè
.xy
¢
=
¢
Ýòî è åñòü òðåáóåìûé ãðàôèê (ðèñ. 61).n
Íà ðèñ. 62, à èçîáðàæåíû ãðàôèêè ôóíêöèé
=y
),(xf= ,3)(,2)( +=-= xfyxfy
à íà ðèñ. 62, á ãðà-
ôèêè ôóíêöèé
)(xfy =
,
).3(),2( +=-= xfyxfy
133. Ãðàôèê êâàäðàòè÷íîé ôóíêöèè. Êâàäðà-
òè÷íîé íàçûâàþò ôóíêöèþ, êîòîðóþ ìîæíî çàäàòü
ôîðìóëîé âèäà
,
2
cbxaxy ++=
ãäå
cba ,,
ëþ-
áûå äåéñòâèòåëüíûå ÷èñëà, ïðè÷åì
.0
¹a
Äëÿ ïî-
ñòðîåíèÿ ãðàôèêà ýòîé ôóíêöèè âûïîëíèì ñëåäóþ-
ùèå ïðåîáðàçîâàíèÿ (íàçûâàåìûå âûäåëåíèåì ïîë-
íîãî êâàäðàòà) êâàäðàòíîãî òðåõ÷ëåíà
:
2
cbxax ++
=+
÷
ø
ö
ç
è
æ
+=++ cx
a
b
xacbxax
22
á)à)
Ðèñ. 63

ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
175174
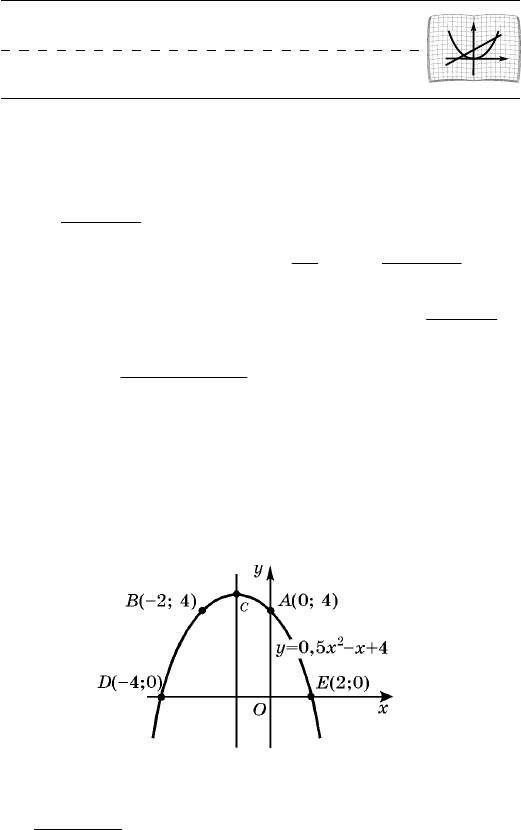
Ï ð è ì å ð. Ïîñòðîèòü ãðàôèê ôóíêöèè
.45,0
2
+--= xxy
q I ñïîñîá: îòûñêàíèå êîîðäèíàò âåðøèíû ïà-
ðàáîëû ïî ôîðìóëàì
.
4
4
;
2
2
00
a
bac
y
a
b
x
-
=-=
Çäåñü à = 0,5, b = 1, c = 4. Çíà÷èò,
=
-
-
=
)
5,0
(
2
1
0
x
;1-=
ó
0
.5,4
)
5,0
(
4
14
)
5,0
(
4
=
-
-×-
=
Èòàê, (1; 4,5)
âåðøèíà ïàðàáîëû. Äëÿ ïîñòðîåíèÿ ãðàôèêà íàéäåì
êîîðäèíàòû åùå íåñêîëüêèõ òî÷åê; íàïðèìåð, (0; 4),
(1; 2,5), (2; 0). Îòìåòèâ âåðøèíó ïàðàáîëû, ïîëó÷åí-
íûå òî÷êè è òî÷êè, ñèììåòðè÷íûå èì îòíîñèòåëüíî
îñè ïàðàáîëû, ñòðîèì òðåáóåìûé ãðàôèê (ðèñ. 64).
II ñïîñîá: ïîñòðîåíèå ïàðàáîëû ïî òî÷êàì ñ îð-
äèíàòîé, ðàâíîé ñâîáîäíîìó ÷ëåíó êâàäðàòíîãî
òðåõ÷ëåíà.
Äëÿ ïîñòðîåíèÿ ãðàôèêà ôóíêöèè (1) íóæíî âû-
ïîëíèòü ïàðàëëåëüíûé ïåðåíîñ ïëîñêîñòè (ñì. ï. 132),
ïîìåñòèâ íà÷àëî íîâîé ñèñòåìû êîîðäèíàò
yOx
¢¢¢
â
òî÷êó
,
4
4
;
2
2
÷
÷
ø
ö
ç
ç
è
æ
-
-
¢
a
bac
a
b
O
è â ïëîñêîñòè
yOx
¢¢¢
ïîñò-
ðîèòü ïàðàáîëó ãðàôèê ôóíêöèè
.)(
2
xay
¢
=
¢
Ïðÿ-
ìàÿ
a
b
x
2
-=
íàçûâàåòñÿ îñüþ ñèììåòðèè ïàðàáî-
ëû, ñëóæàùåé ãðàôèêîì êâàäðàòè÷íîé ôóíêöèè (1),
à òî÷êà, â êîòîðîé ïàðàáîëà ïåðåñåêàåòñÿ ñ åå îñüþ
ñèììåòðèè, âåðøèíîé ïàðàáîëû.
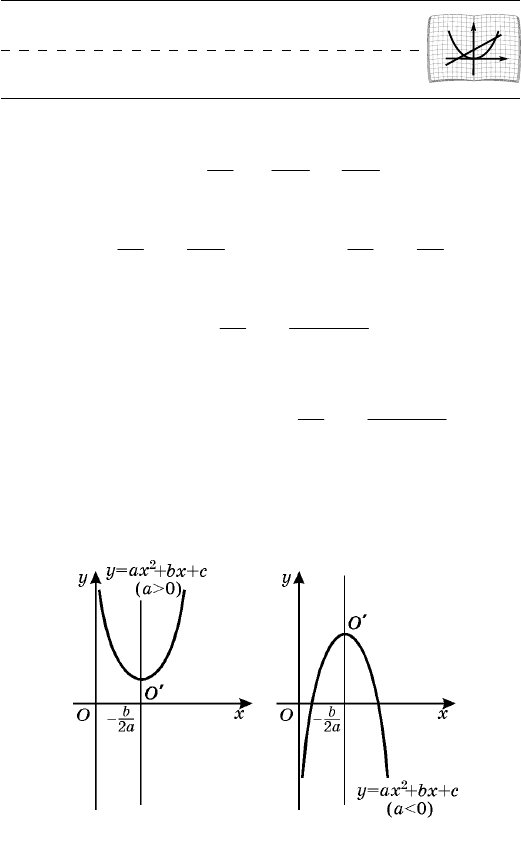
Åñëè à > 0, òî âåòâè ïàðàáîëû, ñëóæàùåé ãðàôèêîì
ôóíêöèè (1), íàïðàâëåíû ââåðõ (ðèñ. 63, à); â ýòîì ñëó-
÷àå ôóíêöèÿ óáûâàåò íà
ú
û
ù
ç
è
æ
-¥-
a
b
2
,
è âîçðàñòàåò íà
.,
2
÷
ø
ö
ê
ë
é
¥+-
a
b
Åñëè æå à < 0, òî âåòâè ïàðàáîëû íàïðàâ-
ëåíû âíèç (ðèñ. 63, á); â ýòîì ñëó÷àå ôóíêöèÿ âîçðàñ-
òàåò íà
ú
û
ù
ç
è
æ
-¥-
a
b
2
,
è óáûâàåò íà
.,
2
÷
ø
ö
ê
ë
é
¥+-
a
b
134. Ñïîñîáû ïîñòðîåíèÿ ãðàôèêà êâàäðàòè÷íîé
ôóíêöèè. Ãðàôèêîì ôóíêöèè
,
2
cbxaxy ++=
ãäå
,0¹a
ÿâëÿåòñÿ ïàðàáîëà (ñì. ï. 133). Äëÿ åå ïîñòðîå-
íèÿ íà ïðàêòèêå èñïîëüçóþòñÿ òðè ñïîñîáà, êîòîðûå
ìû ïðîèëëþñòðèðóåì íà ñëåäóþùåì ïðèìåðå.
x
0
=
õ =1
Ðèñ. 64
ÀËÃÅÁÐÀ
§ 13. Ïðåîáðàçîâàíèÿ ãðàôèêîâ
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
175174
Ï ð è ì å ð. Ïîñòðîèòü ãðàôèê ôóíêöèè
.45,0
2
+--= xxy
q I ñïîñîá: îòûñêàíèå êîîðäèíàò âåðøèíû ïà-
ðàáîëû ïî ôîðìóëàì
.
4
4
;
2
2
00
a
bac
y
a
b
x
-
=-=
Çäåñü à = 0,5, b = 1, c = 4. Çíà÷èò,
=
-
-
=
)
5,0
(
2
1
0
x
;1-=
ó
0
.5,4
)
5,0
(
4
14
)
5,0
(
4
=
-
-×-
=
Èòàê, (1; 4,5)
âåðøèíà ïàðàáîëû. Äëÿ ïîñòðîåíèÿ ãðàôèêà íàéäåì
êîîðäèíàòû åùå íåñêîëüêèõ òî÷åê; íàïðèìåð, (0; 4),
(1; 2,5), (2; 0). Îòìåòèâ âåðøèíó ïàðàáîëû, ïîëó÷åí-
íûå òî÷êè è òî÷êè, ñèììåòðè÷íûå èì îòíîñèòåëüíî
îñè ïàðàáîëû, ñòðîèì òðåáóåìûé ãðàôèê (ðèñ. 64).
II ñïîñîá: ïîñòðîåíèå ïàðàáîëû ïî òî÷êàì ñ îð-
äèíàòîé, ðàâíîé ñâîáîäíîìó ÷ëåíó êâàäðàòíîãî
òðåõ÷ëåíà.
Äëÿ ïîñòðîåíèÿ ãðàôèêà ôóíêöèè (1) íóæíî âû-
ïîëíèòü ïàðàëëåëüíûé ïåðåíîñ ïëîñêîñòè (ñì. ï. 132),
ïîìåñòèâ íà÷àëî íîâîé ñèñòåìû êîîðäèíàò
yOx
¢¢¢
â
òî÷êó
,
4
4
;
2
2
÷
÷
ø
ö
ç
ç
è
æ
-
-
¢
a
bac
a
b
O
è â ïëîñêîñòè
yOx
¢¢¢
ïîñò-
ðîèòü ïàðàáîëó ãðàôèê ôóíêöèè
.)(
2
xay
¢
=
¢
Ïðÿ-
ìàÿ
a
b
x
2
-=
íàçûâàåòñÿ îñüþ ñèììåòðèè ïàðàáî-
ëû, ñëóæàùåé ãðàôèêîì êâàäðàòè÷íîé ôóíêöèè (1),
à òî÷êà, â êîòîðîé ïàðàáîëà ïåðåñåêàåòñÿ ñ åå îñüþ
ñèììåòðèè, âåðøèíîé ïàðàáîëû.
Åñëè à > 0, òî âåòâè ïàðàáîëû, ñëóæàùåé ãðàôèêîì
ôóíêöèè (1), íàïðàâëåíû ââåðõ (ðèñ. 63, à); â ýòîì ñëó-
÷àå ôóíêöèÿ óáûâàåò íà
ú
û
ù
ç
è
æ
-¥-
a
b
2
,
è âîçðàñòàåò íà
.,
2
÷
ø
ö
ê
ë
é
¥+-
a
b
Åñëè æå à < 0, òî âåòâè ïàðàáîëû íàïðàâ-
ëåíû âíèç (ðèñ. 63, á); â ýòîì ñëó÷àå ôóíêöèÿ âîçðàñ-
òàåò íà
ú
û
ù
ç
è
æ
-¥-
a
b
2
,
è óáûâàåò íà
.,
2
÷
ø
ö
ê
ë
é
¥+-
a
b
134. Ñïîñîáû ïîñòðîåíèÿ ãðàôèêà êâàäðàòè÷íîé
ôóíêöèè. Ãðàôèêîì ôóíêöèè
,
2
cbxaxy ++=
ãäå
,0¹a
ÿâëÿåòñÿ ïàðàáîëà (ñì. ï. 133). Äëÿ åå ïîñòðîå-
íèÿ íà ïðàêòèêå èñïîëüçóþòñÿ òðè ñïîñîáà, êîòîðûå
ìû ïðîèëëþñòðèðóåì íà ñëåäóþùåì ïðèìåðå.
x
0
=
õ =1
Ðèñ. 64
