Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

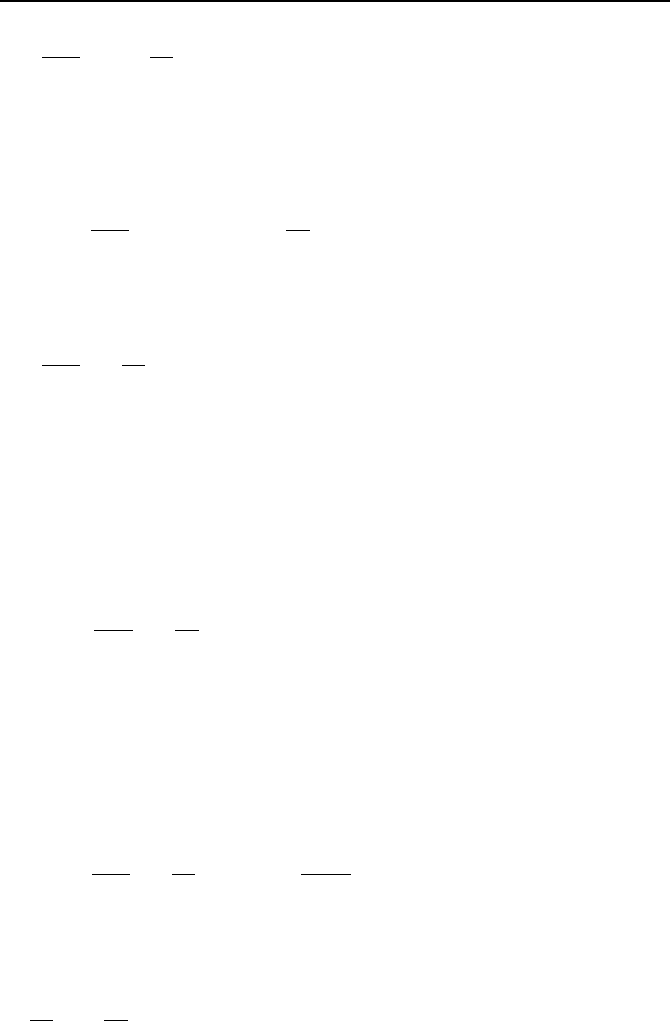
1. Famous Differential Equations 913
02)1(
2
2
=+−+ ny
dx
dy
x
dx
yd
x
VIIb.1.7
The solution to the Laguerre differential equation is known as the Laguerre poly-
nomials.
Gauss differential equation is given as:
0])1([)1(
2
2
=−++−+− y
dx
dy
x
dx
yd
xx
αββαγ
VIIb.1.8
Hermite differential equation is a second-order linear differential equation
given as:
022
2
2
=+− ny
dx
dy
x
dx
yd
x
VIIb.1.9
The solution to the Hermite Differential equation is known as the Hermite poly-
nomials. One of the applications of the Hermite differential equation is in the in-
vestigation of the Schrodinger equation for a harmonic oscillator. Solution to the
Hermit equation is discussed in Section 2.
Legendre differential equation is developed by applying the technique of the
separation of variables in the spherical coordinate system to the Laplace differen-
tial equation, which results in Legendre differential equation:
0)1(2)1(
2
2
2
=++−− ynn
dx
dy
x
dx
yd
x
VIIb.1.10-1
The solution to this second-order linear differential equation is known as Legendre
polynomials. An important application of the Legendre polynomials is that any
polynomial of degree n can be expressed as a linear combination of the first n + 1
Legendre polynomials.
Associated Legendre differential equation is similar to Equation VIIb.1.10-1
except for the coefficient of y, as follows:
0
1
)1(2)1(
2
2
2
2
2
=
¸
¸
¹
·
¨
¨
©
§
−
−++−−
y
x
m
nn
dx
dy
x
dx
yd
x
VIIb.1.10-2
Sturm-Liouville problem is any boundary value problem that is described by a
differential equation in the form of:
[]
0)()()( =++
¸
¹
·
¨
©
§
yxrxq
dx
dy
xp
dx
d
λ
VIIb.1.11

914 VIIb. Engineering Mathematics: Differential Equations
and has two homogeneous boundary conditions, is known as a Sturm-Liouville
problem. We can reduce the Legendre differential equation, Equation VIIb.1.10
from the Sturm-Liouville problem. To demonstrate, we first write the Legendre
differential equation as:
()
0)1(1
2
=++
»
¼
º
«
¬
ª
− ynn
dx
dy
x
dx
d
VIIb.1.12
Comparing Equation VIIb.1.11 with Equation VIIb.1.12, we conclude that p(x) =
1 – x
2
, q(x) = 0, r(x) = 1,
λ
= n(n+1). Therefore, the Legendre differential equa-
tion is a special case of a Sturm-Liouville problem. The Sturm-Liouville problem
possesses the orthogonality property associated with boundary-value differential
equations. Hence, the nontrivial solutions
",,,
321
yyy corresponding to distinct
values
",,,
321
λλλ
of parameter
λ
form an orthogonal system with respect to
the weighting function, p(x).
Bessel differential equation, widely used in various engineering disciplines, is
a second-order linear differential equation and has the general form of:
0)(
222
=−+
»
¼
º
«
¬
ª
yvxm
dx
dy
x
dx
d
x
VIIb.1.13
where m is a parameter and
ν
can be an integer, a fractional number, or zero.
Bessel differential equations appear in such fields as neutron flux distribution in a
cylindrical core, and heat transfer in fins with a triangular profile, as well as elas-
ticity, electric field theory, and aerodynamics. The solution to the Bessel differen-
tial equation is given by:
)()()(
21
xYcxJcxy
νν
+= VIIb.1.14
where J
v
(x) is the Bessel function of the first kind of order v and Y
v
(x) is the Bessel
function of the second kind of order v. These functions are given as:
¦
∞
=
+
++Γ
−=
0
2
)1(!
)2/(
)1()(
k
vk
k
v
vkk
mx
mxJ
VIIb.1.15
)sin(
)()()cos(
)(
π
π
v
mxJmxJv
mxY
vv
v
−
−
=
VIIb.1.16
where J
-v
(mx) is given by:
¦
∞
=
−
−
+−Γ
−=
0
2
)1(!
)2/(
)1()(
k
vk
k
v
vkk
mx
mxJ
VIIb.1.17
where k! is the factorial of k and
Γ is the gamma function as described in Sec-
tion 3.

1. Famous Differential Equations 915
Modified Bessel equation: If in Equation VIIb.1.13, we replace x by ix where
i =
1− , we get the modified Bessel equation as:
0)(][
222
=+− yvxm
dx
dy
x
dx
d
x
VIIb.1.18
The solution to the modified Bessel equation is given as:
)()()(
21
mxKcmxIcxy
νν
+= VIIb.1.19
where I
v
(x) is the modified Bessel function of the first kind of order v and K
v
(x) is
the modified Bessel function of second kind of order v. where
¦
∞
=
+
++Γ
=
0
2
)1(!
)2/(
)(
k
vk
v
vkk
mx
mxI
VIIb.1.20
and
)sin(
)()(
2
)(
π
π
v
mxImxI
mxK
vv
v
−
=
−
VIIb.1.21
where I
-v
(mx) is given by:
¦
∞
=
−
−
+−Γ
=
0
2
)1(!
)2/(
)(
k
vk
v
vkk
mx
mxI
VIIb.1.22
Bessel Type 1 differential equations: It can be shown that equations of the
general form:
0
22
2
2
2
=++ yxb
dx
dy
ax
dx
yd
x
VIIb.1.23
can be expressed in terms of Bessel functions by a change of function from y to
zxy
v
= to get:
0)()(
222
=−+ zvxb
dx
dz
x
dx
d
x
VIIb.1.24
Bessel Type 2 differential equations: Consider second order linear differen-
tial equations in the form of:
0)(
2
=+ yx
dx
dy
x
dx
d
βα
η
VIIb.1.25
where
α
and
β
are positive and
η
may be real or imaginary. Similar to Bessel
Type 1 equations, it can be shown that differential equations in the general form of
Equation VIIb.1.25 can also be reduced to a Bessel differential equation by a
change of variable from x to
µ
tx = to get:
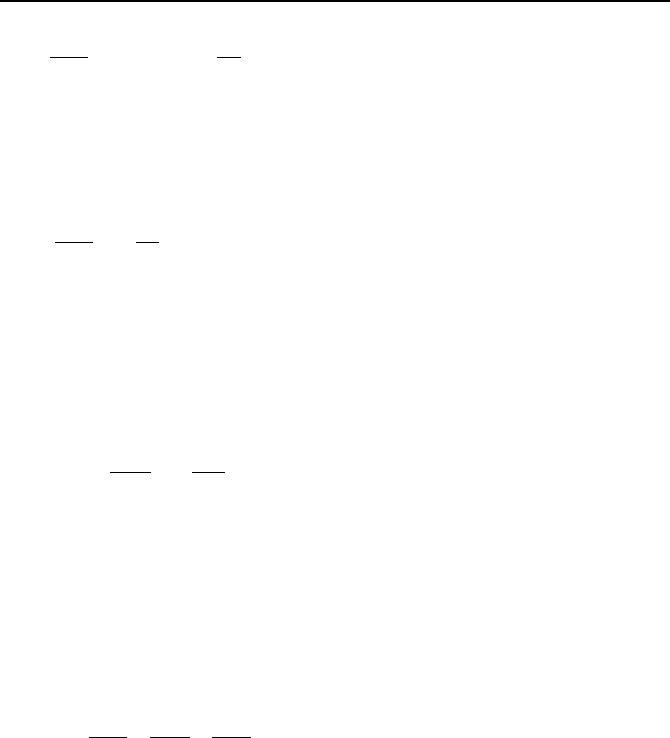
916 VIIb. Engineering Mathematics: Differential Equations
0]1)1([
222
2
2
2
=++−+ yt
dx
dy
t
dx
yd
t
µηαµ
This equation has the form of Equation VIIb.1.23. Hence, the answer can be writ-
ten as
)(
/1/
µµ
ηµ
xZxy
v
v
= where )2/()1( +−−=
αβα
v and )1/(2
αµ
−= v .
The reader can verify that the Euler-Cauchy equation can also be reduced from
Equation VIIb.1.25 if we have
2=−
β
α
to obtain:
0
2
2
2
2
=++ y
dx
dy
x
dx
yd
x
ηα
We can solve this equation by introducing a change of variable from x to x
r
.
1.2. Partial Differential Equations
Many linear partial differential equations representing physical phenomena can be
reduced from:
)(
2
2
2
rf
t
t
+
∂
∂
+
∂
∂
=∇
ψ
µ
ψ
λψ
VIIb.1.26
where the unknown function,
ψ
is ,in general, a function of position and time
(i.e.,
),( trf=
ψ
). Coefficients
µ
and
λ
are some physical parameters and
function f is generally a function of position.
Laplace differential equation is the steady-state homogeneous form of Equa-
tion VIIb.1.26. This equation is used to describe several physical phenomena such
as flow of fluids and flow of heat. The equation in the Cartesian coordinate sys-
tem is written as:
0
2
2
2
2
2
2
2
=
∂
∂
+
∂
∂
+
∂
∂
=∇
z
u
y
u
x
u
u
VIIb.1.27
This is a 2nd-order linear partial differential equation with coefficients
µ
and
λ
as well as function f in Equation VIIb.1.26 being zero. The derivation of this
equation for fluid flow is shown in Chapter IIIa.
Poisson equation is given as:
)(
2
rf=∇
ψ
VIIb.1.28
It describes several physical phenomena. For example, it is the governing equa-
tion in potential flow, describing the velocity potential of an incompressible, irro-
tational, ideal fluid with a continuously distributed sink or source. The Poisson
equation also describes the steady-state temperature distribution in a field with
distributed heat sources. It also describes stress due to elastic torsion of bars.

1. Famous Differential Equations 917
Heat conduction equation, in general form, may be written as:
)(
2
rf
t
+
∂
∂
=∇
ψ
µψ
VIIb.1.29
This equation describes the diffusion phenomenon. If used to determine tempera-
ture distribution due to heat diffusion, it is called the conduction equation, in
which case
1/
µ
α
= where
α
is thermal diffusivity. If Equation VIIb.1.29 is
used as the heat conduction equation, then the function f(r) is described as f(r) = –
kzyxq /),,(
′′′
where q
′′′
is the volumetric heat generation rate and k is the thermal
conductivity of the diffusing medium. The derivation of the heat conduction
equation is shown in Chapter IVa.2.1.
Telephone equation is a one-dimensional equation describing the rate of
change of electric voltage
ψ
along a transmission cable and is written as:
ζψ
ψ
µ
ψ
λ
ψ
+
∂
∂
+
∂
∂
=
∂
∂
t
tx
2
2
2
2
VIIb.1.30
where
LC=
λ
, )( GLRC +=
µ
, and
RG=
ζ
. Here, R and L represent resis-
tance and inductance per unit length of the cable. Also, C and G stand for the ca-
pacitance and conductance to ground per unit length of the cable.
Wave equation is given as:
2
2
2
t∂
∂
=∇
ψ
λψ
VIIb.1.31
where
2
/1 c=
λ
and c is the velocity of sound. This equation is used in the fields
of acoustics, elastic vibration, and electromagnetics. The solution to the unknown
function
ψ
determines the velocity potential in acoustics, displacement in elastic
vibration, and an electric or a magnetic vector in electromagnetism. Equa-
tion VIIb.1.31, in three dimensions, represents the equation for sound waves in air.
In two dimensions it represents the wave equation for a membrane, and in one di-
mension it represents the transverse wave equation in a string. The latter case can
be easily derived from Newton’s second law of motion. To perform such a
derivation, consider a small element of a uniform string having a linear density of
ρ
and being under tension T as shown in Figure VIIb.1.1. Net force in the y-
direction must be set equal to the acceleration of the string. The net force in the
vertical direction is given by:
xdxxy
TTdF )sin()sin(
θθ
−=
+
We now expand the first term in the right side in the Taylor series and use the first
two terms:

918 VIIb. Engineering Mathematics: Differential Equations
y
x
T
T
ds
dy
dx
θ
x
θ
x+dx
Figure VIIb.1.1. An elemental string in tension
dx
x
T
Tdx
x
T
TTTdF
x
x
x
xxdxxy
∂
∂
=−
»
¼
º
«
¬
ª
∂
∂
+=−=
+
)sin(
)sin(
)sin(
)sin()sin()sin(
θ
θ
θ
θθθ
From Newton’s 2
nd
law (
2
2
dt
yd
dmdF
= ):
2
2
)(
t
y
x
y
T
x
∂
∂
=
∂
∂
∂
∂
ρ
Since tension T is constant, it can be removed from the derivative. Also represent-
ing T/
ρ
= b
2
we obtain:
2
2
22
2
1
t
y
bx
y
∂
∂
=
∂
∂
VIIb.1.31-1
Note that b has the dimension of velocity. Having derived the one-dimensional
wave equation, it is useful to briefly describe the fundamentals of mechanical
waves. A wave is the motion of a disturbance in a medium. Wavelength (
λ
), fre-
quency (
v
), and the propagation velocity (b) are used to characterize waves.
Wavelength is the minimum distance between any two points on a wave that
behave identically. Frequency is the rate at which the disturbance repeats itself.
The wave amplitude is the maximum displacement of a particle disturbed by the
wave. Waves are either transverse or longitudinal. In transverse waves, the mo-
tion of the particles of the medium is perpendicular to the wave velocity and in
longitudinal waves, the motion of particles is parallel to the wave velocity. The
propagation velocity (i.e., the velocity at which a wave travels) depends on the
properties of the medium being disturbed. While waves generally require a me-
dium to travel (referred to as mechanical waves), the electromagnetic waves such
as photon travel in vacuum (i.e. require no medium).
Schroedinger wave equation in its general time-dependent form is given as:
t
tr
itrrVtr
m
∂
∂
=+∇−
),(
),()(),(
2
2
2
K
=
K
G
K
=
ψ
ψψ
VIIb.1.32

2. Analytical Solutions to Differntial Equations 919
where 1−=i ,
π
2/h== , where Plank’s constant h = 6.626E-34 J-s. In Equa-
tion VIIb.1.32, m is mass, V is potential energy, and r is the location vector. Po-
tential energy in general is a function of location and time, V = V(x, y, z, t) but
most often only a function of location. Equation VIIb.1.32, as suggested by Erwin
Schroedinger in 1926, has some similarities with Equation VIIb.1.31, the classic
wave equation. However, unlike the wave equation derived above, the Schroed-
inger equation as a hypothesis, can only be verified and has no rigorous deriva-
tion. As such, Equation VIIb.1.32 is a statement similar to that of Newton’s sec-
ond law of motion, which has no proof. Furthermore,
ψ
in Equation VIIb.1.32
(referred to as the wave function) is not displacement. Rather; it is a measure of
probability known as probability amplitude and the square of its absolute value is
known as the probability density (
2
ψ
). By definition, dxdydz
2
ψ
represents the
probability that measurement of the particle’s position at the time t finds the parti-
cle in the volume element dV about the point x, y, and z. Solution to the
Schrödinger equation is given in Section 2.
2. Analytical Solutions to Differntial Equations
Differential equations can be divided into two categories. The first category in-
cludes equations for which we can find analytical solutions. The second category
includes equations for which, due to complications, we cannot find the analytical
solutions and have to solve numerically. We start with the first category due to
the importance of analytical solutions, then we deal with the second category.
2.1. Solution to First-Order Linear Ordinary Differential Equations
The general form of a first order linear differential equation is given as:
)()( xqyxp
dx
dy
=+ VIIb.2.1
To seek an analytic solution in closed form, we note that if the equation was writ-
ten as:
[]
)()( xGyxF
dx
d
= VIIb.2.2
the solution could be readily found as:
[]
CdxxG
xF
y +=
³
)(
)(
1
VIIb.2.3
where C is the constant of integration. To express the unknown functions F(x)
and G(x) in terms of the specified functions p(x) and q(x), respectively, we carry
out the differential on the left-hand side of Equation VIIb.2.2, and rearrange the
results to get:

920 VIIb. Engineering Mathematics: Differential Equations
)(
)()(
)(
1
xF
xG
y
dx
xdF
xFdx
dy
=
»
¼
º
«
¬
ª
+
By comparing with the original equation, we find that:
)(
)(
)(
1
xp
dx
xdF
xF
=
Integrating this first order equation, the unknown function can be determined as
³
=
dxxp
exF
)(
)( . Similarly, by comparing the right-hand sides, we find that:
)(
)(
)(
xq
xF
xG
=
From here, the unknown function G(x) can be determined as
³
=
dxxp
exqxG
)(
)()( . Substituting F(x) and G(x) in the solution (i.e. Equa-
tion VIIb.2.3) yields:
¿
¾
½
¯
®
+
»
¼
º
«
¬
ª
=
³
³³
−
Cdxexqey
dxxpdxxp )()(
)( VIIb.2.4
Example: Find the solution to the following equation, given y = 1 for x = 1:
xy
dx
dy
x sin2 =+
We divide both sides by x ≠ 0, to find p(x) = 2/x and q(x) = sin x/x. We first find:
³
µ
¶
´
==
2
ln2)( x
x
dx
dxxp
We then find:
µ
¶
´
dxe
x
x
x
2
ln
sin
=
³
xdxx sin = sin x – x cos x
Substituting in Equation VIIb.2.4, we obtain:
{}
Cxxxey
x
+−=
−
cossin
2
ln
Applying the boundary condition, C ≅ 0.7. Hence,
{}
7.0cossin
2
ln
+−=
−
xxxey
x
Special Case: In many engineering applications, both p(x) and q(x) are con-
stant values, say P and Q. In this case, Equation VIIb.2.4 simplifies to:
P
Q
Cey
Px
+=
−
VIIb.2.5
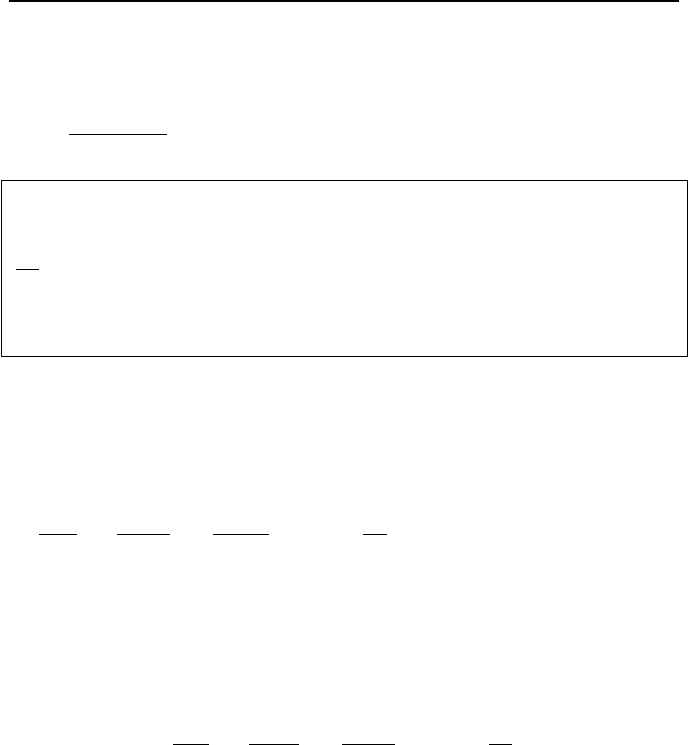
2. Analytical Solutions to Differntial Equations 921
The constant of integration can be found from a boundary condition. For exam-
ple, if at x = 0, we have y = y
0
, then C = y
0
– Q/P. The final solution for this spe-
cial case becomes:
Px
e
PQy
PQy
−
=
−
−
)/(
)/(
0
VIIb.2.6
Example: Find the solution to the following first order equation where coeffi-
cients a and b are given constants. For the boundary condition, use x = 0, y = a/b.
bay
dx
dy
=+
Solution: For this case, P = a, Q = b, and y
o
= a/b. Hence, from Equa-
tion VIIb.2.6, y = (a/b – b/a)e
–ax
+ b/a.
2.2. Solution to Higher Order Linear Ordinary Differential Equations
Solution to Linear Differential Equations with Constant Coefficients
Such equations have the general form of:
)(
1
2
2
2
1
1
1
xqya
dx
dy
a
dx
yd
a
dx
yd
a
dx
yd
nn
n
n
n
n
n
n
=+++++
−
−
−
−
−
" VIIb.2.7
where a
1
through a
n
are constants. This linear non-homogeneous differential
equation of order n is also written in the shorthand form of:
Dy=q(x) VIIb.2.8
where D is a linear operator
nn
n
n
n
n
n
n
a
dx
d
a
dx
d
a
dx
d
a
dx
d
D
+++++=
−
−
−
−
−
1
2
2
2
1
1
1
"
We can verify that a solution in the form of y = e
rx
satisfies the homogeneous form
of Equation VIIb.2.7 so that
0)(
1
2
2
1
1
=+++++=
−
−−
rx
nn
nnn
ecrarararDy " VIIb.2.9
the solution to Equation VIIb.2.9 may yield real or complex values for r.
Real and distinct roots. The solution to the homogeneous Equation VIIb.2.9
becomes:
¦
=
=
n
i
xr
iH
i
ecy
1
For example, the solution to the differential equation

922 VIIb. Engineering Mathematics: Differential Equations
023
2
2
=+−
dx
dy
dx
yd
has two distinct roots for r
2
– 3r + 2 = 0 namely, r
1
= 1 and r
2
= 2. Hence, the so-
lution is y = c
1
e
x
+ c
2
e
2x
.
Real but not distinct roots. Consider the case where the solution to Equation
VIIb.2.9 yields real roots but roots (r
1
) are repeated n-times where n is the degree
of r in Equation VIIb.2.9. In such case, the solution is given by:
xr
n
n
excxcxccy
1
)(
12
321
−
++++= "
For example, the linear differential operator for
018218
2
2
3
3
=−+−
dx
dy
dx
yd
dx
yd
is r
3
–8r
2
+21r –18 =0 which yields r
1
= 2, r
2
= 3, and r
3
= 3. Hence, the solution
to the differential equation becomes:
xxx
xecececy
3
3
3
2
2
1
++=
As an another example, consider
01464
2
2
3
3
4
4
=+−+−
dx
dy
dx
yd
dx
yd
dx
yd
The linear operator is given by r
4
– 4r
3
+ 6r
2
–4r + 1 =0. This equation yields 4-
fold roots of r
1
= 1. Solution to the differential equation then becomes
x
excxcxccy )(
3
4
2
321
+++=
Complex and distinct roots. If the solution to Equation VIIb.2.9 yields dis-
tinct complex roots such as r
1
= a + ib and r
2
= a – ib, then the solution has the
form of:
)cossin(
21
bxcbxcey
ax
+=
For example, the linear operator for
054
2
2
=+−
dx
dy
dx
yd
is r
2
– 4r +5 = 0, which has the roots of r
1
= 2 + i and r
2
= 2 – i. Hence, the solu-
tion to the differential equation is found as:
)cossin(
21
2
xcxcey
x
+=
