Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

2. Analytical Solutions to Differntial Equations 923

Complex but not distinct roots. If the roots are complex and not distinct, then

the solution becomes:

]cos)(sin)[(

321

bxxcxcxccbxxcxcxccey

nnnn

ax −

+++

−

+++++++++= ""

For example, the linear operator for

=++ y

is r

+ 2r

+ 1 =0, which has two sets of identical roots r

= r

= i and r

= r

= -i.

The solution to the equation is:

xxccxxccy cos)(sin)(

4321

+++= .

Solution to Equidimensional Linear Differential Equations

These are linear non-homogeneous differential equations with coefficients that are

functions of the independent variable in the form of:

)(

xqyc

=++++

−

" VIIb.2.10

Such equations are known as Euler-Cauchy differential equations. This equation

can be transformed into an nth-order linear differential equation, given by Equa-

tion VIIb.2.7, by change of independent variable from x to

xz ln= .

Solution to Differential Equations by Reduction of Order

This interesting method, as generally applied to second order linear differential

equations, requires us to have one of the solutions to find the other solution. If we

have one solution to the following general form of the second order differential

equation as y

(x),

)()()(

xqyxa

=++ VIIb.2.11

the second solution, as shown by Hildebrand, is then given by:

)(

xycdx

xzy

cxy

= VIIb.2.12

where c

and c

are arbitrary constants and z is given by

dxxa

)(

. One par-

ticular solution is obtained from:

924 VIIb. Engineering Mathematics: Differential Equations

xzy

dxxzyxq

xyxy

)(

)()(

VIIb.2.13

No additional constants of integration are necessary for y

(x), since already ar-

bitrary constant c

and c

are chosen. The complete solution is then given by:

y(x) = y

(x) + y

(x) VIIb.2.14

To ensure that the answers y

and y

are not linearly dependent, we should show that

the Wronskian determinant is not zero. The Wronskian determinant is given by:

−

dxxa

ecyyW

)(

121

),(

As an example, let’s try to solve the following differential equation by the method

of reduction of order:

023

=+−

Suppose the first answer is in the form of y

= e

. We find the second answer by

first calcualting:

dxdxxa

eeez

3)(

−

===

then find y

from Equation VIIb.2.12:

[]

xxxx

ececcdxecexycdx

xzy

cxy

12112

)(

+=+=

Note that y

(x) = 0. Since c

and c

are arbitrary constants, the answer is therefore

y(x) = c

+ c

Solution to Differential Equations by Laplace Transform

This approach is based on converting differential equations to algebraic equations

by Laplace transform, finding the unknown in the converted equation, and finding

the solution to the differential equation by an inverse transform. In this process,

the properties of the Laplace transform as outlined in Section VIIIa-1 and the

functions with associated Laplace transforms of Table VIIa.1.1 are employed. For

example to solve

=+ y

with the boundary conditions of y(0) = 0 and dy(0)/dx = 2, we first find the

Laplace transform of each term. The Laplace transform of the first term is ob-

2. Analytical Solutions to Differntial Equations 925

tained from the general relation for the transform of the derivatives repeated here

from Section 1 of this chapter:

)0()0(')0(][][

)1(21)( −−−

−−−−=

nnnnn

ffsfsfsf "AA

Hence, the equation becomes; 0

9]/)0()0(

[

=+−− ydxdysyys . Substituting for

the values at x = 0 from the boundary conditions we get;

)9(

=+ ys

From the inverse transform we find; y = 2/3 sin 3x.

Solution to Differential Equations by Power Series

The solution to a large class of second order differential equations, where the coef-

ficients are functions of the independent variable, can be found in terms of a

power series. The general homogeneous form of such equations is given as:

0)()()(

=++ yxR

VIIb.2.15

To demonstrate the solution by power series, let’s solve an example where P(x) =

Q(x) = R(x) = 1. We now assume a solution to exist in the form of:

"++++++=

210

xAxAxAxAxAAy VIIb.2.16

Integrate Equation VIIb.2.16 twice for dy/dx and d

y/dx

, substitute in Equation

VIIb.2.15, and collecting similar terms we get:

0]123[]62[]2[

432321210

=+++++++++ "xAAAxAAAAAA

For the summation of terms with the increasing power of x to become equal to

zero, we must have the coefficient of each term to be equal to zero:

6/]2[

2/][

213

102

AAA

+−=

As seen above, we have solved for all the unknown coefficients in terms of two

coefficients A

and A

, which in turn, can be found from the boundary conditions.

We may generalize this to obtain an algorithm. To do this, we write Equation

VIIb.2.16 in the more convenient way as:

∞

)(

xAxy VIIb.2.17

The first and second differentials of Equation VIIb.2.17 become:

926 VIIb. Engineering Mathematics: Differential Equations

¦¦

¦¦¦

∞

−

∞

−

∞

−

∞

−

∞

−

−=−=

−=−==

)1()1(

)(

)1()1(

)(

xAiixAii

xyd

xAixAixiA

xdy

where we have manipulated the indices to facilitate collection of the coefficients

of like powers. We may now substitute these terms in Equation VIIb.2.15 to ob-

tain:

¦¦¦

∞

−

∞

−

∞

−

=+−+−

0)1()1(

xAxAixAii

This equation can be further simplified when the coefficients of like powers are

grouped together:

0])1()1([

=+−+−

−

−−

∞

xAAiAii VIIb.2.18

From Equation VIIb.2.18, we can find the algorithm as:

)1(/])1[(

−+−−=

−−

iiAAiA

iii

This algorithm is also referred to as the recurrence formula. To compare with our

previous calculation of A

, we now choose i = 2 which results in A

= − [A

]/2,

as was found earlier.

2.3. Solution to Solvable Non-linear Ordinary Differential

Equations

Generally, the non-linear differential equations cannot be solved by analytical

means to obtain answers in closed form. However, there are certain types of non-

linear differential equations, which are amenable to analytical solution. These are

discussed next.

Separable Equations

These are implicit equations that can be grouped in terms of the dependent and in-

dependent variables. For example, any equation in the form of:

0)()()()(

4321

=+ dyyfxfdxyfxf

can be grouped as:

)(

=+ dy

2. Analytical Solutions to Differntial Equations 927

Let’s consider a specific example such as 0

=+ dydxxy . This equation can be

written as xdx + dy/y

= 0, integration of which gives x

/2 –1/y = C. A second ex-

ample for non-linearity involving dy/dx is (dy/dx)

+ f(y) +C = 0. Equations of this

sort can be solved as (dy/dx)

= –[f(y) + C]. If the right-hand side is real then,

dy/dx =

])([ Cyf +−± . This is a first order equation in the form of:

Cyf

±=

+− ])([

VIIb.2.19

This can be solved if the numerator is amenable to integration. As an exercise, the

reader may solve the case of f(x) = e

and C = –1. It should be mentioned that

Equation VIIb.2.19 was obtained by multiplying both sides by dx and dividing

both sides by the radical. In doing so, we have excluded the special case of f(y) =

–C. To see if this is indeed a solution, it must be verified separately. The reader

may try another exercise where f(y) = –y and C = 1 which shows that f(y) = –C is

indeed a solution.

Exact First-Order Equations

According to the definition of Section VIIa.1, the following differential equation

0),(),(),( =+= dyyxNdxyxMyxdf

is an exact differential equation if:

yxN

yxM

∂

∂ ),(),(

Since the derivative of (x, y) is given as:

),(),(

),( =

∂

= dy

yxf

yxdf

we then conclude that M

yxf

∂

∂ ),(

and N

yxf

∂

∂ ),(

. Integrating the first rela-

tion gives:

)(),(),(

ygdxyxMyxf

where g(y) in this equation is the constant of integration. We can find its value by

taking the derivative with respect to y and using the second relation:

Nygdx

yxM

yxf

∂

)('

),(),(

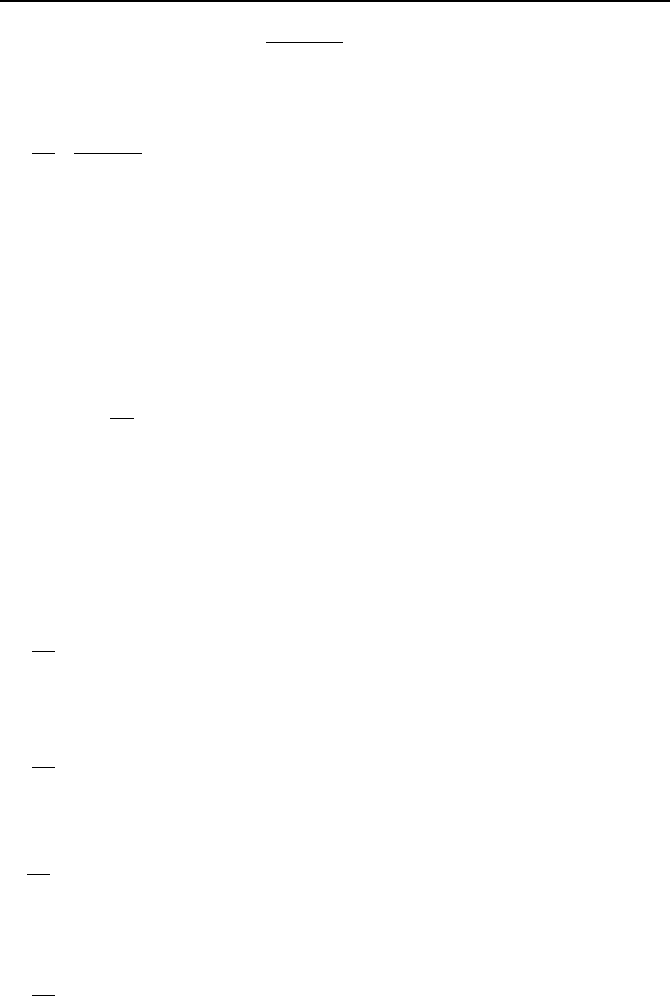
928 VIIb. Engineering Mathematics: Differential Equations

Solving to get

∂

−=

yxM

Nyg

),(

)('

, from which g(y) is found and the

equation is solved. Let’s try an example. The goal is to solve the following non-

linear differential equation

this equation can also be written in the more familiar form of (x

+ y

) dx + 2xy dy

= 0. Hence, M = x

+ y

and N = 2xy. We first see if the expression (x

+ y

) dx +

2xy dy is an exact differential. This can be easily verified that the derivative of M

with respect to y (i.e. 2y) is the same as the derivative of N with respect to x (i.e.

2y). Similarly, we may verify this for N. To solve the differential equation, we in-

tegrate M to get f(x, y) = x

/3 + xy

+ g(y). We now take the derivative of this with

respect to y and set it equal to N to get: 2xy + g’(y) = 2xy. From here, g(y) = C.

Hence, the solution to the differential equation is given as:

Cxy

yxf ++=

),(

where C is found from the boundary condition. The following is left for exercise,

M = 2x + y and N = x + 2y.

Change of Variable

This technique is applicable to first-order nonlinear differential equations. For ex-

ample, the Bernoulli differential equation:

yxQyxP

)()( =+

can be transformed into a linear differential equation by a change of dependent

variable from y to z = y

1-n

to obtain:

)()1()()1( xQnzxPn

−=−+

resulting in a first-order linear differential equation. The second example includes

the Riccati equation:

)()()(

xRyxQyxP

=++

If u(x) is one solution to the Riccati differential equation, the substitution y = u(x)

+ 1/z will transform the Riccati equation:

)(2)]()([ xPzxQxuP

=+−

in to a first-order linear differential equation. The third example includes equa-

tions in the form of:

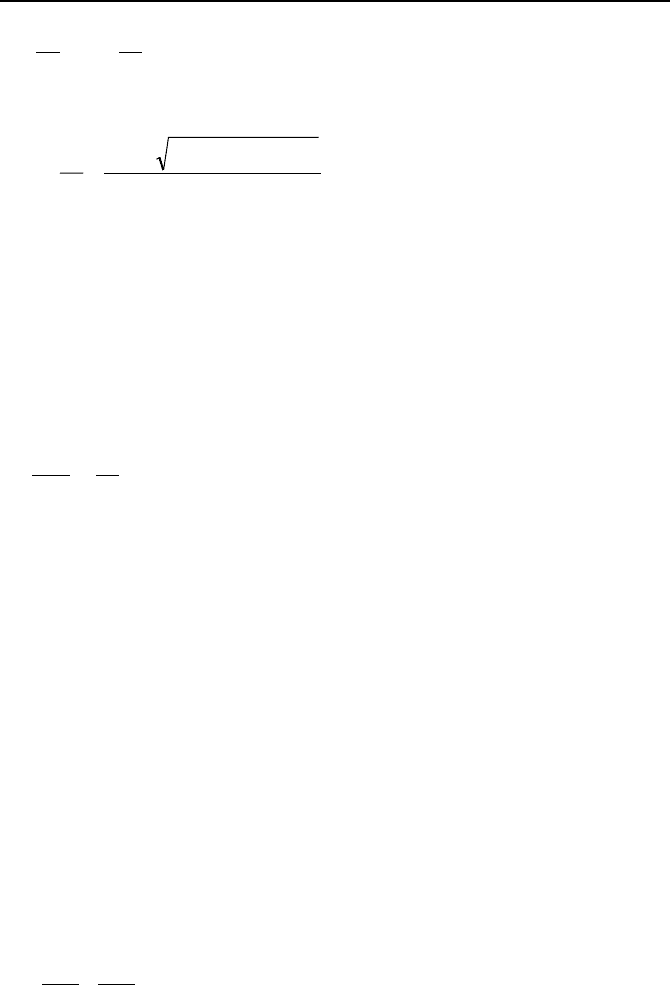
2. Analytical Solutions to Differntial Equations 929

)()(

xfyc

=++

VIIb.2.20

By assuming dy/dx = z, we may solve Equation VIIb.2.20 as an algebraic equation

for z to obtain:

)]([4

xfyccc

−−±−

VIIb.2.21

Depending on the function f(x) and coefficients c

and c

, Equation VIIb.2.21 may

be amenable to integration. This can be tried, as an exercise, for the case where c

= 2− , c

= 4, and f(x) = 4x – 1.

Reduction of Order

This method is applied to the second-order differential equations lacking a vari-

able (i.e. lacking either x, y or both). In such cases, we can reduce the order of the

equation by using a substitute for a derivation. For example, consider the follow-

ing second-order nonlinear equation:

0)(

If we assume dy/dx = M, then d

y/dx

= dM/dx. Therefore, dM/M

= – dx. This

can now be easily solved to find 1/M

= 2x + C. Substituting for M, we get dy =

dx/(2x + C)

1/2

, which is a simple first order equation.

2.4. Solution to Partial Differential Equations

Generally, partial differential equations of mathematical physics and engineering

applications are solved by the method of separation of variables. In this method,

we seek particular product solutions. To illustrate this method, we present two

examples. The first example deals with determination of temperature distribution

in a plate and the second deals with determination of the probability amplitude of

a subatomic particle.

Solution to the Heat Conduction Equation

The idea is to determine temperature distribution (i.e., T = f(x, y)) in a plate as

shown in the figure under steady state conditions. The two-dimensional heat con-

duction equation in steady state, as derived in Chapter IVa, reduces to the two-

dimensional Laplace differential equation:

∂

VIIb.2.22

subject to the x-direction and y-direction boundary conditions as follows. In the x-

direction, T(0, y) = 0 and T(a, y) = 0. In the y-direction, T(x, 0) = 0 and T(x, b) =

f(x) as shown in Figure VII.2.1.

930 VIIb. Engineering Mathematics: Differential Equations

T(x, b) = f(x)

T(0, x) = 0

T(a, y) = 0T(0, y) = 0

Figure VIIb.2.1. Boundary conditions for obtaining temperature distribution in a rectangle

Our goal is to find a product solution such as

)()(),( yYxXyxT

= VIIb.2.23

Substituting Equation VIIb.2.23 to VII.2.22, we find:

Separating variables, we obtain

±==−

VIIb.2.24

where the right side of this equation is only a function of x and the left side is only

a function of y. This is possible only if both sides are equal to a constant such as

. By choosing the square of a real number, we made sure that k

is positive. The

next task is to choose an appropriate sign for k

, which is discussed next. Mean-

while, note that by the method of separation of variables, we managed to replace a

second order linear partial differential equation with two second-order linear ordi-

nary differential equations, which can be readily solved.

To solve Equation VIIb.2.24, we must determine which sign we should use for

. The selection of a sign for the constant k

depends on the boundary conditions.

A direction involving homogeneous boundary conditions must be associated with

a periodic function and the direction involving nonhomogeneous boundary condi-

tion must be associated with an exponential function. For example, in Fig-

ure VIIb.2.1, the homogeneous boundary conditions are specified in the x-

direction whereas the y-direction includes one nonhomogeneous boundary condi-

tion. Therefore, we select the plus sign for k

to get:

=+ Xk

VIIb.2.25

Recall that Equation VIIb.2.25 is a Sturm-Liouville problem. Hence, constant k

will result in appearance of the eigenvalues. The solution to Equation VIIb.2.25

subject to the above boundary conditions was obtained in Section VIIb.1.1 as:

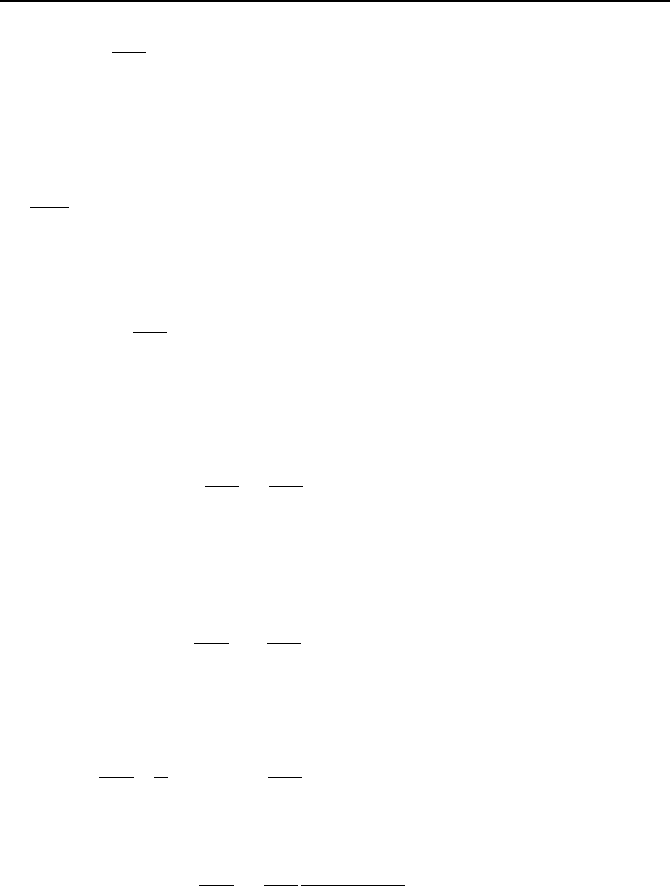
2. Analytical Solutions to Differntial Equations 931

sin=

where n is a positive integer, n =

",3,2,1

. Choosing plus sign for k

, the equation

involving y becomes:

=− Yk

VIIb.2.26

The solution to Equation VIIb.2.26 is given in Section VIIb.2.2 as:

sinh=

Since X(x)Y(y) is a particular solution to Equation VIIb.2.22, the following is also

a solution:

∞

sinsinh),(

CyxT

ππ

Where C

= A

. To find the set of unknown coefficients C

, we use the last

boundary condition:

Cxf

∞

0sinsinh)(

ππ

We now use the Fourier series expansion for f(x) to find the unknown coefficients

sin)(

sinh

ππ

Therefore,

∞

)/sinh(

sinsinh),(

abn

ayn

CyxT

πππ

VIIb.2.27

Thus, temperature at any point in the plate can be determined from Equa-

tion VIIb.2.27. Following the same logic of the two-dimensional temperature dis-

tribution in the Cartesian coordinate system, as an exercise, the reader may solve

for the three-dimensional temperature distribution. To do this, consider a rectan-

gular parallelepiped where all five faces are maintained at zero and the sixth face

is maintained at a specified temperature T(x, y, z = c) = f(x, y).

932 VIIb. Engineering Mathematics: Differential Equations

Solution to Schrödinger Wave Equation

Erwin Schrödinger discovered the wave equation for matter waves. It was Max

Born who interpreted the Shroedinger – de Broglie waves as waves of probability,

which became the wave mechanics version of quantum mechanics. Consider the

classical properties of electromagnetic waves in free space such as frequency ( v ),

Historical perspective. Physicists have traditionally tried to unify all physical phenom-

ena under one set of mathematical rules. For example, Newton applied the terrestrial laws

to describe the motion of celestial bodies. Boltzmann integrated thermodynamics into clas-

sical mechanics, Ampere and Faraday demonstrated that electricity and magnetism are two

sides of the same coin, and James Clerk Maxwell explained optics in terms of electromag-

netic waves (Figure VIIb.2.2). This pursuit of unification continued until around the turn of

the 20

century, when classical physics then tried to explain every phenomenon in terms of

two independent branches; classical mechanics and electromagnetism. However, with this

approach classical physics could not describe phenomena on a microscopic scale. For ex-

ample, blackbody radiation, the photoelectric effect, and the emission of sharp spectral lines

by atoms in a gas discharge could not be explained within the framework of classical phys-

ics. The most challenging task facing classical physics was explaining the nature of light,

which behaves as both wave and particle. In classical mechanics, every elementary object

is either wave, obeying Maxwell’s equations or a particle, obeying Newtonian laws. The

discrepancy between the Newtonian concept of relative motion and Michelson’s optical ex-

periment in 1881 gave birth to Einstein’s theory of relativity. Prior to Michelson’s experi-

ment, the nature of light was based solely on the electromagnetic theory of Maxwell dating

back to 1862. Treating light only as an electromagnetic wave requires a medium for light to

travel through an empty space. Still, classical physics was in dire need of modernization to

be able to explain such new challenging phenomena as photoelectric effects and emission of

sharp spectral light in a gas discharge. The shortcomings of classical physics led to the de-

velopment of modern physics (based on wave or quantum mechanics), which quantitatively

describes the behavior of nature on a microscopic scale. In quantum mechanics, where par-

ticles and waves are two distinct modes of behavior shared by all objects, there is no dis-

tinction between wave and particle as in classical theories. We may then consider the clas-

sical mechanics as a special case of the more general wave mechanics.

Figure VIIb.2.2. A plane monochromatic electromagnetic wave

The discovery of quantum physics proceeded in two tracks. Max Plank, Neils Bohr, and

Werner Heisenberg’s work led to the realization that the allowed values of energy exchange

between subatomic particles are discrete. The second track based on the works of Albert

Einstein, Louis de Broglie, Erwin Schrödinger, and Max Born focused on the duality of

light as both wave and particle. Paul Dirac later showed that these two tracks are entirely

equivalent.