Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

where

 ¼



tan

1



For large Q, this can be approximated as



max





log o=o

ðÞ

M  M



where M and M

are the moduli at two different frequencies o and o

. Note the

resemblance of this expression to equation (3.8.7) for the standard linear solid and

equation (3.8.8) for the nearly constant Q model.

Uses

The equations presented in this section are used for phenomenological modeling of

attenuation and velocity dispersion of seismic waves.

Assumptions and limitations

The equations presented in this section assume that the material is linear, dissipative,

and causal.

3.9 Kramers–Kronig relations between velocity dispersion and Q

Synopsis

For linear viscoelastic systems, causality requires that there be a very specific

relation between velocity or modulus dispersion and Q; that is, if the dispersion is

1/Q

log(w)

−1

(w)

M(w)

Figure 3.8.5 Schematic of the constant Q model in the frequency domain.

127 3.9 Kramers–Kronig relations between velocity and Q

completely characterized for all frequencies then Q is known for all frequencies and

vice versa.

We can write a viscoelastic constitutive law between the stress and strain compon-

ents as

ðtÞ¼

"ðtÞ

where r(t) is the relaxation function and

denotes convolution. Then in the Fourier

domain we can write

~ðoÞ¼MðoÞ

"ðoÞ

where M(o) is the complex modulus. For r(t) to be causal, in the frequency domain

the real and imaginary parts of M(o)/(io) must be Hilbert transform pairs (Bourbie

et al., 1987):

ðoÞ¼



þ1

1

ðÞM

ð0Þ



d

  o

ðoÞM

ð0Þ¼



þ1

1

ðÞ



d

  o

where M

(0) is the real part of the modulus at zero frequency, which results because

there is an instantaneous elastic response from a viscoelastic material. If we express

this in terms of

1

ðoÞsgnðoÞ

ðoÞ

then we obtain

1

ðoÞ¼

joj

M

ðoÞ

þ1

1

ðÞM

ð0Þ



d

  o

ð3:9:1Þ

and its inverse

ðoÞM

ð0Þ¼

o



þ1

1

ðÞM

ðÞ

jj

d

ð  oÞ

ð3:9:2Þ

From these we see the expected result that a larger attenuation is generally

associated with larger dispersion. Zero attenuation requires zero velocity dispersion.

One never has more than partial information about the frequency dependence of

velocity and Q, but the Kramers–Kronig relation allows us to put some constraints on

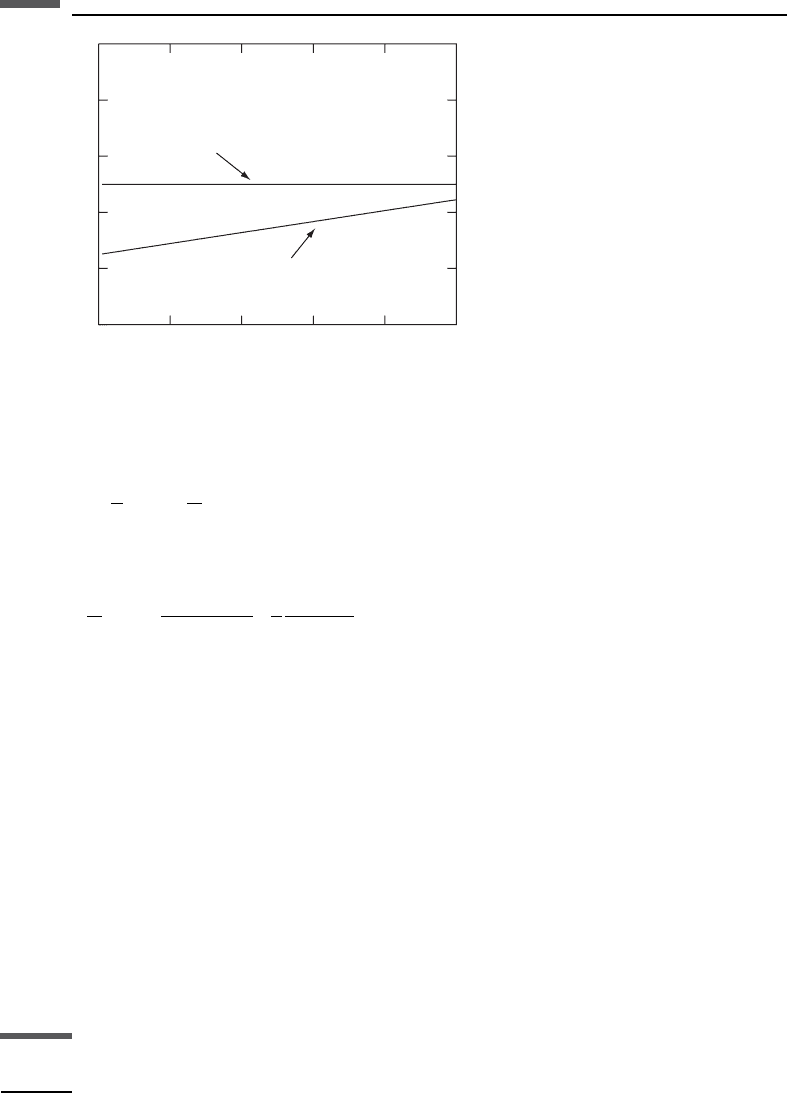
the material behavior. For example, Lucet (1989) measured velocity and attenuation

at two frequencies (1 kHz and 1 MHz) and used the Kramers–Kronig relations to

compare the differences with various viscoelastic models, as shown schematically

in Figure 3.9.1. Using equation (3.9.1), we can determine the expected ratio of

128 Seismic wave propagation

low-frequency modulus or velocity, V

, and high-frequency modulus or velocity, V

for various functional forms of Q (for example, constant Q or nearly constant Q).

In all cases, linear viscoelastic behavior should lead to an intercept of V

¼ 1at

1/Q ¼ 0. Mechanisms with peaked attenuation curves between the measurement points

will generally cause a larger dispersion, which appears as a steeper negative slope.

Uses

The Kramers–Kronig equations can be used to relate velocity dispersion and Q in

linear viscoelastic materials.

Assumptions and limitations

The Kramers–Kronig equations apply when the material is linear and causal.

3.10 Waves in layered media: full-waveform synthetic seismograms

Synopsis

One of the approaches for computing wave propagation in layered media is the use of

propagator matrices (Aki and Richards, 1980; Claerbout, 1985). The wave variables

of interest (usually stresses and particle velocity or displacements) at the top and

bottom of the stack of layers are related by a product of propagator matrices, one for

each layer. The calculations are done in the frequency domain and include the effects

of all multiples. For waves traveling perpendicularly to n layers with layer velocities,

densities, and thicknesses V

, r

, and d

, respectively



k¼1



where S and W are the Fourier transforms of the wave variables s and w, respectively.

For normal-incidence P-waves, s is interpreted as the normal stress across each

interface, and w is the normal component of the particle velocity. For normal-incidence

Constant Q

Nearly

constant Q

Other

Dispersion V

1/Q

Figure 3.9.1 Lucet’s (1989) use of the Kramers–Kronig relations to compare high- and

low-frequency measured velocities and Q with various viscoelastic models.

129 3.10 Full-waveform synthetic seismograms

S-waves, s is the shear traction across each interface, and w is the tangential

component of the particle velocity. Each layer matrix A

has the form

cos



i

sin





sin



cos



where o is the angular frequency.

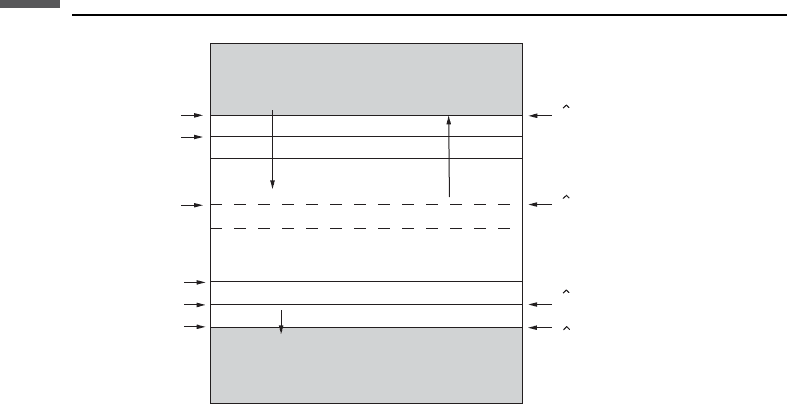
Kennett (1974, 1983) used the invariant imbedding method to generate the

response of a layered medium recursively by adding one layer at a time (Figure

3.10.1). The overall reflection and transmission matrices,

and

, respectively,

for downgoing waves through a stack of layers are given by the following recursion

relations:

ðkÞ

¼ R

ðkÞ

þ T

ðkÞ

ðkþ1Þ

ðkÞ

I  R

ðkÞ

ðkþ1Þ

ðkÞ

1

ðkÞ

ðkþ1Þ

ðkÞ



I  R

ðkÞ

ðkþ1Þ

ðkÞ



1

ðkÞ

where R

ðkÞ

; T

ðkÞ

; R

ðkÞ

; and T

ðkÞ

are just the single-interface downward and upward

reflection and transmission matrices for the kth interface:

ðkÞ

Pðk1Þ

cos 

k1

Sðk1Þ

cos 

k1



1=2

Sðk1Þ

cos 

k1

Pðk1Þ

cos 

k1



1=2

ðkÞ



PðkÞ

cos 



k1

Pðk1Þ

cos 

k1



1=2



PðkÞ

cos 



k1

Sðk1Þ

cos 

k1



1=2



SðkÞ

cos 



k1

Pðk1Þ

cos 

k1



1=2



SðkÞ

cos 



k1

Sðk1Þ

cos 

k1



1=2

ðkÞ

PðkÞ

cos 

SðkÞ

cos 



1=2

SðkÞ

cos 

PðkÞ

cos 



1=2

ðkÞ



k1

Pðk1Þ

cos 

k1



PðkÞ

cos 



1=2



k1

Pðk1Þ

cos 

k1



SðkÞ

cos 



1=2



k1

Sðk1Þ

cos 

k1



PðkÞ

cos 



1=2



k1

Sðk1Þ

cos 

k1



SðkÞ

cos 



1=2

130 Seismic wave propagation

with

¼ M

1

M ¼

sin 

k1

cos 

k1

sin 

cos 

cos 

k1

sin 

k1

cos 

sin 

Sðk1Þ

sin 

k1

cos 

k1

Sðk1Þ

ð1  2 sin



k1

Þ 2I

SðkÞ

sin 

cos 

SðkÞ

ð1  2 sin



I

Pðk1Þ

ð1  2 sin



k1

Þ I

Sðk1Þ

sin 2

k1

PðkÞ

ð1  2 sin



ÞI

SðkÞ

sin 2

N ¼

sin 

k1

cos 

k1

sin 

cos 

cos 

k1

sin 

k1

cos 

sin 

Sðk1Þ

sin 

k1

cos 

k1

Sðk1Þ

ð1  2 sin



k1

Þ 2I

SðkÞ

sin 

cos 

SðkÞ

ð1  2 sin



Pðk1Þ

ð1  2 sin



k1

ÞI

Sðk1Þ

sin 2

k1

I

PðkÞ

ð1  2 sin



Þ I

SðkÞ

sin 2

where I

P(k)

= r

P(k)

and I

S(k)

= r

S(k)

are the P and S impedances, respectively,

of the kth layer, and y

and f

are the angles made by the P- and S-wave vectors

with the normal to the kth interface. The elements of the reflection and transmis-

sion matrices R

ðkÞ

; T

ðkÞ

; R

ðkÞ

; and T

ðkÞ

are the reflection and transmission

coefficients for scaled displacements, which are proportional to the square root

of the energy flux. The scaled displacement u

is related to the displacement u by

¼ u

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

V cos :

Interface 1

Interface 2

Interface k

Interface n − 1

Interface n

Interface n +1

Homogeneous half-space

(k)

(n)

(1)

(n +1)

Layer 1

Layer 2

Layer k

Layer n − 1

Layer n

Transmitted

Homogeneous half-space

Incident

Reflected

Figure 3.10.1 Recursively determined transfer functions in a layered medium.

131 3.10 Full-waveform synthetic seismograms

For normal-incidence wave propagation with no mode conversions, the reflection

and transmission matrices reduce to the scalar coefficients:

ðkÞ



k1

 



k1

þ 

; R

ðkÞ

¼R

ðkÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



k1



k1

þ 

; T

ðkÞ

¼ T

ðkÞ

The phase shift operator for propagation across each new layer is given by E

ðkÞ

expðiod

cos 

PðkÞ

Þ 0

0 expðiod

cos 

SðkÞ



where y

and f

are the angles between the normal to the layers and the directions of

propagation of P- and S-waves, respectively. The terms

and

are functions of o

and represent the overall transfer functions of the layered medium in the frequency

domain. Time-domain seismograms are obtained by multiplying the overall transfer

function by the Fourier transform of the source wavelet and then performing an

inverse transform. The recursion starts at the base of the layering at interface n þ 1

(Figure 3.10.1). Setting R

ðnþ1Þ

¼ 0 and T

ðnþ1Þ

¼ I simulates a

stack of layers overlying a semi-infinite homogeneous half-space with properties

equal to those of the last layer, layer n. The recursion relations are stepped up through

the stack of layers one at a time to finally give

ð1Þ

and

ð1Þ

, the overall reflection and

transmission response for the whole stack.

Calculate the P-wave normal-incidence overall reflection and transmission functions

ð1Þ

and

ð1Þ

recursively for a three-layered medium with layer properties as follows:

Pð1Þ

¼ 4000 m=s;

Pð2Þ

¼ 3000 m=s;

Pð3Þ

¼ 5000 m=s;



¼ 2300 kg=m

;



¼ 2100 kg=m

;



¼ 2500 kg=m

;

¼ 100 m

¼ 50 m

¼ 200 m

The recursion starts with

ð4Þ

= 0 and

ð4Þ

= 1. The normal-incidence reflection

and transmission coefficients at interface 3 are

ð3Þ



Pð2Þ

 

Pð3Þ



Pð2Þ

þ 

Pð3Þ

¼0:33; R

ð3Þ

¼R

ð3Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



Pð2Þ



Pð3Þ



Pð2Þ

þ 

Pð3Þ

¼ 0:94; T

ð3Þ

¼ T

ð3Þ

and the phase factor for propagation across layer 3 is

132 Seismic wave propagation

ð3Þ

¼ expði2fd

Pð3Þ

Þ¼expði2f 200=5000Þ

where f is the frequency. The recursion relations give

ð3Þ

¼R

ð3Þ

ð4Þ

ð3Þ

1  R

ð3Þ

ð4Þ

ð3Þ

ð4Þ

ð3Þ

1  R

ð3Þ

ð4Þ

ð3Þ

The recursion is continued in a similar manner until finally we obtain

ð1Þ

and

ð1Þ

The matrix inverse

½I  R

ðkÞ

ðkþ1Þ

ðkÞ



1

is referred to as the reverberation operator and includes the response caused by all

internal reverberations. In the series expansion of the matrix inverse

½I  R

ðkÞ

ðkþ1Þ

ðkÞ



1

¼I þ R

ðkÞ

ðkþ1Þ

ðkÞ

þ R

ðkÞ

ðkþ1Þ

ðkÞ

ðkþ1Þ

ðkÞ

þ

the first term represents the primaries and each successive term corresponds to

higher-order multiples. Truncating the expansion to m þ 1 terms includes m internal

multiples in the approximation. The full multiple sequence is included with the exact

matrix inverse.

Uses

The methods described in this section can be used to compute full-wave seismo-

grams, which include the effects of multiples for wave propagation in layered media.

Assumptions and limitations

The algorithms described in this section assume the following:



layered medium with no lateral heterogeneities;



layers are isotropic, linear, elastic; and



plane-wave, time-harmonic propagation.

133 3.10 Full-waveform synthetic seismograms

3.11 Waves in layered media: stratigraphic filtering

and velocity dispersion

Synopsis

Waves in layered media undergo attenuation and velocity dispersion caused by multiple

scattering at the layer interfaces. The effective phase slowness of normally incident

waves through layered media depends on the relative scales of the wavelength and layer

thicknesses and may be written as S

eff

¼S

þS

. The term S

is the ray theory slowness

of the direct ray that does not undergo any reflections and is just the thickness-weighted

average of the individual layer slownesses. The individual slownesses may be complex

to account for intrinsic attenuation. The excess slowness S

(sometimes called the

stratigraphic slowness) arises because of multiple scattering within the layers.

A flexible approach to calculating the effective slowness and travel time follows from

Kennett’s (1974) invariant imbedding formulation for the transfer function of a layered

medium. The layered medium, of total thickness L, consists of layers with velocities

(inverse slownesses), densities, and thicknesses, V

, r

,andl

, respectively.

The complex stratigraphic slowness is frequency dependent and can be calculated

recursively (Frazer, 1994)by

ioL

j¼1

1  R



As each new layer j þ 1 is added to the stack of j layers, R is updated according to

jþ1

¼r

jþ1



jþ1

1  R



jþ1

(with R

¼ 0) and the term

ln½t

jþ1

ð1  R

jþ1



jþ1

1



is accumulated in the sum. In the above expressions, t

and r

are the transmission and

reflection coefficients defined as

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



jþ1



þ 

jþ1



jþ1

 



þ 

jþ1

whereas y

¼ exp(iol

) is the phase shift for propagation across layer j and o is the

angular frequency. The total travel time is T ¼ T

þ T

, where T

is the ray theory

travel time given by

134 Seismic wave propagation

j¼1

and T

is given by

¼ Re

j¼1

1  R



!"#

The deterministic results given above are not restricted to small perturbations in the

material properties or statistically stationary geology.

Calculate the excess stratigraphic travel time caused by multiple scattering for a

normally incident P-wave traveling through a three-layered medium with layer

properties as follows:

Pð1Þ

¼ 4000 m=s;

¼ 2300 kg=m

; l

¼ 100 m

Pð2Þ

¼ 3000 m=s;

¼ 2100 kg=m

; l

¼ 50 m

Pð3Þ

¼ 5000 m=s;

¼ 2500 kg=m

; l

¼ 200 m

The excess travel time is given by

¼ Re

j¼1

1  R



!"#

The recursion begins with R

¼ 0,

¼r



1  R



where

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



þ 

¼ 0:98



 



þ 

¼0:19

¼ exp(i2pfl

) ¼ exp(i2pf100/4000) with f as the frequency.

The recursion is continued to obtain R

and R

. Setting t

¼ 1 and r

¼ 0

simulates an impedance-matching homogeneous infinite half-space beneath layer 3.

135 3.11 Stratigraphic filtering and velocity dispersion

Finally, the excess travel time, which is a function of the frequency, is obtained by

taking the real part of the sum as follows:

¼ Re

i2f

1  R





þ ln

1  R





þ ln

1  R





The effect of the layering can be thought of as a filter that attenuates the input

wavelet and introduces a delay. The function

AðoÞ¼expðioxS

Þ¼expðioT

(where S

is assumed to be real in the absence of any intrinsic attenuation) is

sometimes called the stratigraphic filter.

The O’Doherty–Anstey formula (O’Doherty and Anstey, 1971; Banik et al., 1985)

jAðoÞj  expð

RðoÞT

approximately relates the amplitude of the stratigraphic filter to the power spectrum

RðoÞ of the reflection coefficient time series r() where

ðxÞ¼

=Vðx

is the one-way travel time. Initially the O’Doherty–Anstey formula was obtained by a

heuristic approach (O’Doherty and Anstey, 1971). Later, various authors substanti-

ated the result using statistical ensemble averages of wavefields (Banik et al., 1985),

deterministic formulations (Resnick et al., 1986), and the concepts of self-averaged

values and wave localization (Shapiro and Zien, 1993). Resnick et al. (1986) showed

that the O’Doherty–Anstey formula is obtained as an approximation from the

exact frequency-domain theory of Resnick et al. by neglecting quadratic terms in

the Riccatti equation of Resnick et al. Another equivalent way of expressing the

O’Doherty–Anstey relation is

ImðS



RðoÞ

Mð2oÞ

Here 1/Q is the scattering attenuation caused by the multiples, and

MðoÞ is the power

spectrum of the logarithmic impedance fluctuations of the medium,

ln½ðÞVðÞ  ln½ðÞVðÞ

,where 

denotes a stochastic ensemble average.

Because the filter is minimum phase, o Re(S

)ando Im(S

) are a Hilbert transform pair,

ReðS



t



RðoÞg

where H{·} denotes the Hilbert transform and dt is the excess travel caused by

multiple reverberations.

136 Seismic wave propagation