Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.

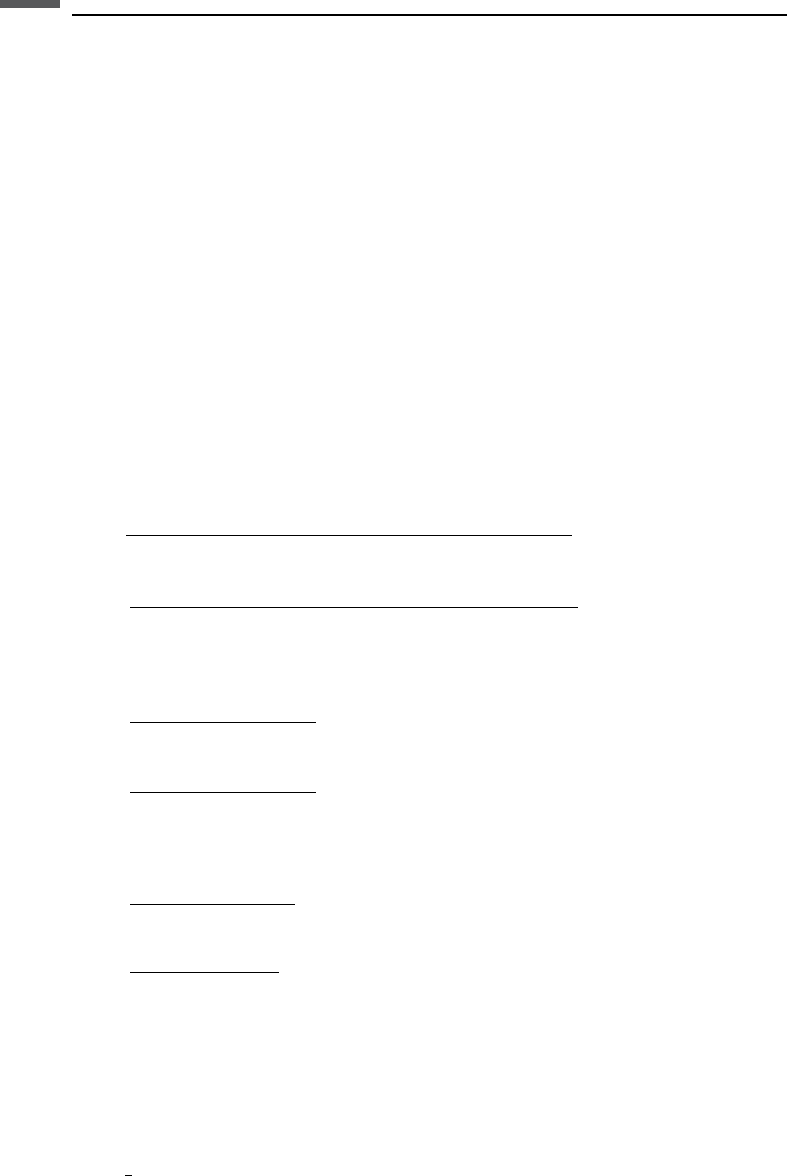
In practice, the shear or extensional velocity is calculated from the observed
resonant frequency, most often at the fundamental mode, where n ¼ 1.
Porous, fluid-saturated rods
Biot’s theory has been used to extend Pochhammer’s method of analysis for fluid-
saturated porous rods (Gardner, 1962; Berryman, 1983). The dependence of the
velocity and attenuation of longitudinal waves on the skeleton and fluid properties
is rather complicated. The motions of the solid and the fluid are partly parallel to the
axis of the cylinder and partly along the radius. The dispersion relations are obtained
from plane-wave solutions of Biot’s equations in cylindrical (r, y,z) coordinates. For
an open (unjacketed) surface boundary condition the o–k
z
dispersion relation is given
by (in the notation of Berryman, 1983)
D
open
¼
a
11
a
12
a
13
a
21
a
22
0
a
31
a
32
a
33
¼ 0
a
11
¼
½ðC
HÞk
2
þ
þ 2
fr
k
2
z
J
0
ðk
þ
aÞþ2
fr
k
r
þ
J
1
ðk
þ
aÞ=a
ð
þ
Þ
a
12
¼
½ðH C
þ
Þk
2
2
fr
k
2
z
J
0
ðk
aÞ2
fr
k
r
J
1
ðk
aÞ=a
ð
þ
Þ
a
13
¼2
fr
k
sr
½k
sr
J
0
ðk
sr
aÞJ
1
ðk
sr
aÞ=a
a
21
¼
ðM
CÞk
2
þ
J
0
ðk
þ
aÞ
ð
þ
Þ
a
22
¼
ðC M
þ
Þk
2
J
0
ðk
aÞ
ð
þ
Þ
a
23
¼ 0
a
31
¼
2i
fr
k
z
k
rþ
J
1
ðk
þ
aÞ
ð
þ
Þ
a
32
¼
2i
fr
k
z
k
r
J
1
ðk
aÞ
ð
þ
Þ
a
33
¼
fr
ðk
2
s
2k
2
z
Þk
sr
J
1
ðk
sr
aÞ=ðik
z
Þ
k
2
r
¼ k
2
k
2
z
; k
2
sr
¼ k
2
s
k
2
z
k
2
s
¼ o
2
ð
fl
2
=qÞ
fr
k
2
þ
¼
1
2
b þ f
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðb f Þ
2
þ 4cd
q
157 3.15 Waves in cylindrical rods: the resonant bar

k
2
¼
1
2
b þ f þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðb f Þ
2
þ 4cd
q
b ¼ o
2
ðM
fl
CÞ=
c ¼ o
2
ð
fl
M qCÞ=
d ¼ o
2
ð
fl
H CÞ=
f ¼ o
2
ðqH
fl
CÞ=
¼ MH C
2
¼ d=ðk
2
bÞ¼ðk
2
f Þ=c
H ¼ K
fr
þ
4
3
fr
þ
ðK
0
K
fr
Þ
2
ðD K
fr
Þ
C ¼
ðK
0
K
fr
ÞK
0
ðD K
fr
Þ
M ¼
K
2
0
ðD K
fr
Þ
D ¼ K
0
½1 þ ðK
0
=K
fl
1Þ
¼ð1 Þ
0
þ
fl
q ¼
fl
iFðÞ
o
where
K
fr
, m
fr
¼effective bulk and shear moduli of rock frame: either the dry frame or the high-
frequency unrelaxed “wet frame” moduli predicted by the Mavko–Jizba squirt theory
K
0
¼ bulk modulus of mineral material making up rock
K
fl
¼ effective bulk modulus of pore fluid
f ¼ porosity
r
0
¼ mineral density
r
fl
¼ fluid density
a ¼ tortuosity parameter (always greater than 1)
¼ viscosity of the pore fluid
k ¼ absolute permeability of the rock
o ¼ angular frequency of the plane wave.
The viscodynamic operator F(z) incorporates the frequency dependence of viscous
drag and is defined by
FðÞ¼
1
4
TðÞ
1 þ 2iTðÞ=
158 Seismic wave propagation

TðÞ¼
ber
0
ðÞþibei
0
ðÞ
berðÞþibeiðÞ
¼
e
i3=4
J
1
ðe
i=4
Þ
J
0
ðe
i=4
Þ
¼ðo=o
r
Þ
1=2
¼
oh
2
fl
1=2
where ber( ) and bei( ) are the real and imaginary parts of the Kelvin function,
respectively, J
n
( ) is a Bessel function of order n, and h is the pore-size parameter.
The pore-size parameter h depends on both the dimensions and shape of the pore
space. Stoll (1974) found that values of between
1
6
and
1
7
for the mean grain diameter
gave good agreement with experimental data from several investigators. For spherical
grains, Hovem and Ingram (1979) obtained h ¼ fd/[3(1 – f)], where d is the grain
diameter.
This dispersion relation gives the same results as Gardner (1962). When the surface
pores are closed (jacketed) the resulting dispersion relation is
D
closed
¼
a
11
a
12
a
13
a
31
a
32
a
33
a
41
a
42
a
43
¼ 0
a
41
¼
k
rþ
J
1
ðk
þ
aÞ
þ
; a
42
¼
k
r
þ
J
1
ðk
aÞ
þ
; a
43
¼ k
sr
J
1
ðk
sr
aÞ
fl
=q
For open-pore surface conditions the vanishing of the fluid pressure at the surface
of the cylinder causes strong radial motion of the fluid relative to the solid. This
relative motion absorbs energy, causing greater attenuation than would be present in a
plane longitudinal wave in an extended porous saturated medium (White, 1986).
Narrow stop bands and sharp peaks in the attenuation can occur if the slow P-wave
has wavelength l < 2.6a. Such stop bands do not exist in the case of the jacketed,
closed-pore surface. A slow extensional wave propagates under jacketed boundary
conditions but not under the open-surface condition.
Uses
The results described in this section can be used to model wave propagation and
geometric dispersion in resonant bar experiments.
Assumptions and limitations
The results described in this section assume the following:
an isotropic, linear, homogeneous, and elastic–poroelastic rod of solid circular
cross-section;
for elastic rods the cylindrical surface is taken to be free of tractions; and
for porous rods, unjacketed and jacketed surface boundary conditions are assumed.
159 3.15 Waves in cylindrical rods: the resonant bar

3.16 Waves in boreholes
Synopsis
Elastic wave propagation in the presence of a cylindrical fluid-filled borehole involves
different modes caused by internal refraction, constructive interference and trapping
of wave energy in the borehole. The theory of borehole wave propagation has been
described in the books by White (1983), Paillet and Cheng (1991), and Tang and
Cheng (2004), where references to the original literature may be found. The dispersion
characteristics of borehole wave modes depend strongly on the shear wave velocity of
the elastic medium surrounding the borehole. Two scenarios are usually considered:
“fast” formation when the S-wave velocity in the formation is greater than the
borehole fluid velocity and “slow” formation when the S-wave velocity in the formation
is slower than the borehole fluid velocity. Wave modes are guided by the borehole only
when the formation S-wave velocity is greater than the phase velocity of the modes;
otherwise the modes become leaky modes, radiating energy into the formation.
In fast formations, pseudo-Rayleigh modes or shear normal modes exist above
characteristic cut-off frequencies. The pseudo-Rayleigh mode is strongly dispersive
and is a combined effect of reflected waves in the fluid and critical refraction along
the borehole walls. The phase velocity of the pseudo-Rayleigh wave at the cut-off
frequency drops from the shear wave velocity of the formation and approaches the
fluid velocity at high frequencies. In slow formations pseudo-Rayleigh modes do not
exist. Stoneley waves in boreholes refer to waves along the borehole interface. At low
frequencies the Stoneley waves are referred to as tube waves. Stoneley waves exist at
all frequencies and in both fast and slow formations. “Leaky P” modes exist in slow
formations and are dominated by critical refraction of P-waves at the borehole wall.
They lose energy by conversion to shear waves. Higher-order modes include the
dipole or flexural mode and the quadrupole or screw mode (Tang and Cheng, 2004).
Isotropic elastic formation
A low-frequency (static) analysis for a thick-walled elastic tube of inner radius b and
outer radius a, with Young’s modulus E, and Poisson ratio n, containing fluid with
bulk modulus B, and density r, gives the speed of tube waves as (White, 1983)
c
t
¼
1
B
þ
1
M
1=2
M ¼
Ea
2
b
2
ðÞ
21þ nðÞa
2
þ b
2
ðÞ2nb
2
½
For a thin-walled tube with thickness h ¼ða bÞ; a b; and M Eh=2b: For a
borehole in an infinite solid a b and the speed of the tube wave in the low-
frequency limit is
160 Seismic wave propagation
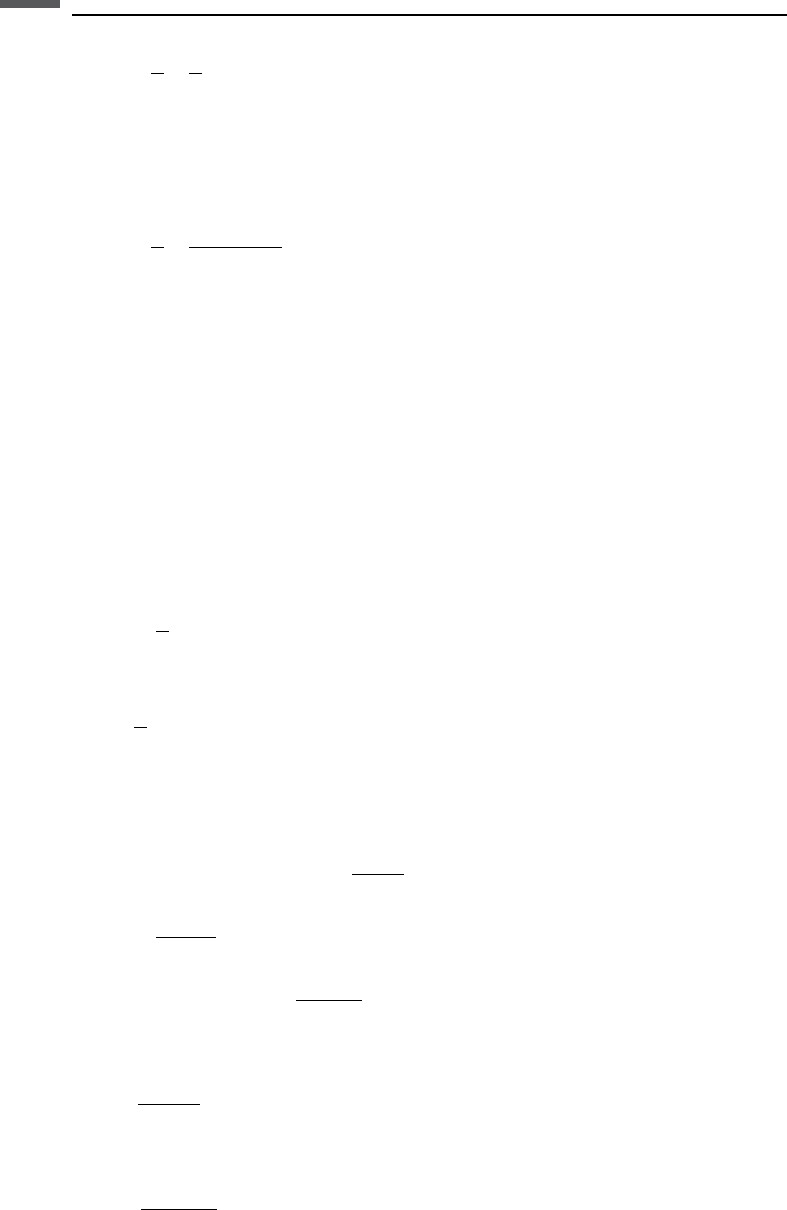
c
t
¼
1
B
þ
1
1=2
where m is the shear modulus of the formation. For a borehole with a casing of
thickness h, inner radius b, and Young’s modulus E, the tube wave velocity (in the
low-frequency limit) is
c
t
¼
1
B
þ
1
þ Eh =2b
1=2
The o–k dispersion relation gives a more complete description of the modes. The
dispersion relation (or period equation) yields characteristic cut-off frequencies and
phase velocities as a function of frequency for the different modes (Paillet and Cheng,
1991; Tang and Cheng, 2004). For a cylindrical borehole of radius R, in an infinite,
isotropic, elastic formation with Lame
´
constants l and m, and density r, and open-
hole boundary conditions at the interface, the dispersion relation is given by (in the
notation of Tang and Cheng, 2004)
Dðo; k Þ¼
M
11
M
12
M
13
M
14
M
21
M
22
M
23
M
24
M
31
M
32
M
33
M
34
M
41
M
42
M
43
M
44
¼ 0
M
11
¼
n
R
I
n
fRðÞfI
nþ1
fRðÞ
M
12
¼pY
1
pRðÞ
M
13
¼
n
R
K
n
sRðÞ
M
14
¼iksY
1
sRðÞ
M
21
¼
f
o
2
I
n
fRðÞ
M
22
¼ 2k
2
2
o
2
K
n
pRðÞþ
2p
2
R
Y
2
pRðÞ
M
23
¼
2ns
2
R
Y
3
sRðÞ
M
24
¼ 2iks
2
2
K
n
sR
ðÞ
þ
2iks
2
R
Y
2
sR
ðÞ
M
31
¼ 0
M
32
¼
2np
2
R
Y
3
pRðÞ
M
33
¼s
2
2
Y
4
sRðÞ
M
34
¼
2ikns
2
R
Y
3
sRðÞ
161 3.16 Waves in boreholes
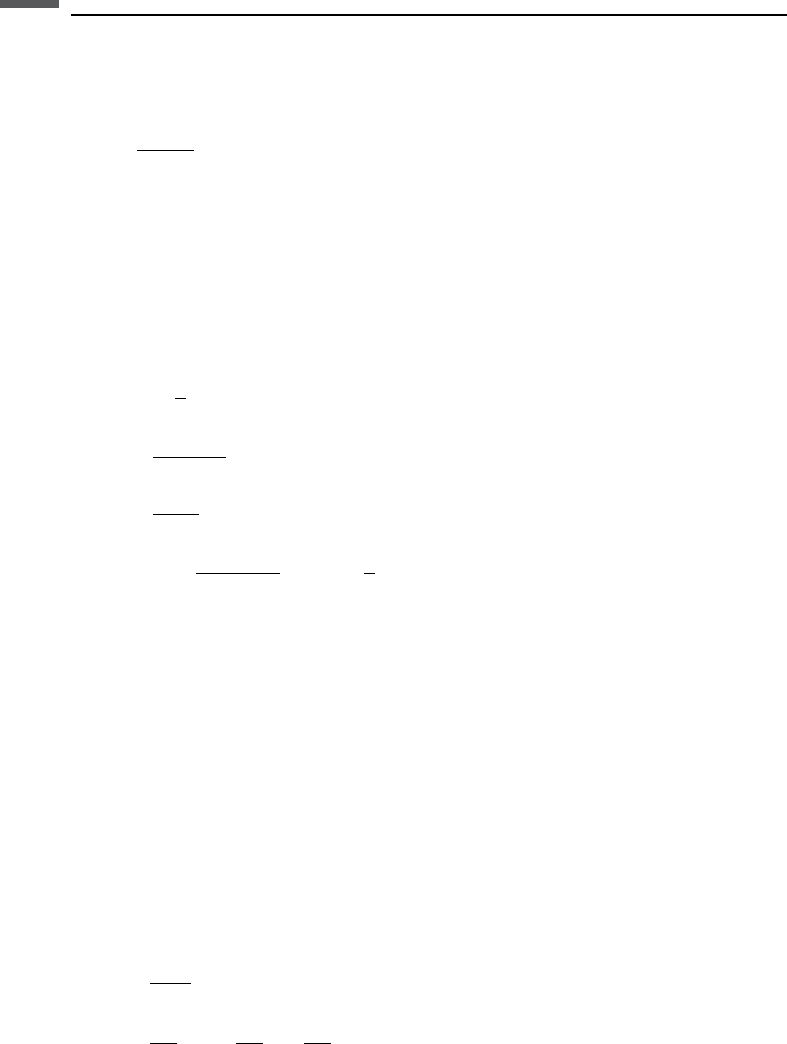
M
41
¼ 0
M
42
¼2ikp
2
Y
1
pRðÞ
M
43
¼
ikn
2
R
K
n
sRðÞ
M
44
¼ k
2
þ s
2
s
2
Y
1
sRðÞ
where I
n
and K
n
are the modified Bessel functions of the first and second kind,
respectively, of order n. The azimuthal order number, n, controls the azimuthal
variations, with n ¼ 0, 1, and 2 corresponding to monopole, dipole, and quadrupole
modes, respectively. In the above expressions Y
i
denotes the following combinations
of modified Bessel functions:
Y
1
xðÞ¼
n
x
K
n
xðÞþK
nþ1
xðÞ
Y
2
x
ðÞ
¼
nn 1ðÞ
x
K
n
x
ðÞ
þ K
nþ1
x
ðÞ
Y
3
xðÞ¼
1 n
x
K
n
xðÞþK
nþ1
xðÞ
Y
4
xðÞ¼ 1 þ
2nn 1ðÞ
x
2
K
n
xðÞþ
2
x
K
nþ1
xðÞ
Other terms in the expressions are:
o ¼ angular frequency
k ¼ axial wavenumber
p ¼ k
2
k
2
1=2
¼ compressional radial wavenumber
s ¼
k
2
k
2
1=2
¼ shear radial wavenumber
f ¼
k
2
k
2
f
1=2
¼ radial wavenumber in the borehole fluid
k
¼ o = ¼ compressional wavenumber
k
¼ o= ¼ shear wavenumber
k
f
¼ o =
f
¼ acoustic wavenumber in borehole fluid
where a and b are the P- and S-wave velocities in the formation, and
f
is the
compressional wave velocity in the borehole fluid. From the roots of the dispersion
relation Dðo; kÞ¼0, the phase and group velocities of the wave modes are obtained as
V
phase
¼
o
kðoÞ
V
group
¼
do
dk
¼
@D
@k
@D
@o
The roots and the partial derivatives have to be calculated numerically.
Transversely isotropic (TI) elastic formation
The elastic properties of the transversely isotropic formation are given by the five
independent components of the elastic stiffness tensor (c
11
, c
13
, c
33
, c
44
, c
66
), and
162 Seismic wave propagation
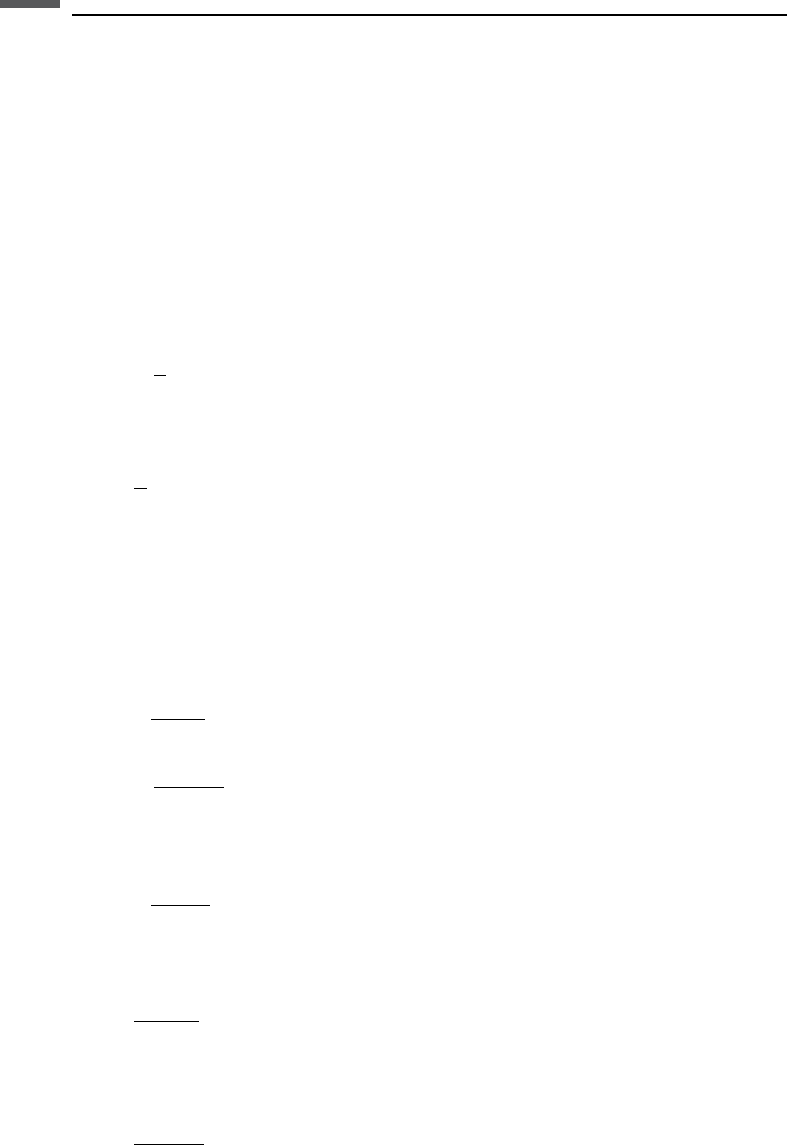
r denotes the density. The TI symmetry axis is along the z-axis and the borehole axis
coincides with the symmetry axis. The borehole radius is R, with borehole fluid
density
f
; and compressional wave velocity
f
: For open-hole boundary conditions
the dispersion relation is given by (Tang and Cheng, 2004)
Dðo; kÞ¼
Q
11
Q
12
Q
13
Q
14
Q
21
Q
22
Q
23
Q
24
Q
31
Q
32
Q
33
Q
34
Q
41
Q
42
Q
43
Q
44
¼ 0
Q
11
¼
n
R
I
n
fRðÞfI
nþ1
fRðÞ
Q
12
¼1 þ ika
0
ðÞq
p
Y
1
q
p
R
Q
13
¼
n
R
K
n
q
sh
RðÞ
Q
14
¼ik þ b
0
ðÞq
sv
Y
1
q
sv
RðÞ
Q
21
¼
f
o
2
I
n
fRðÞ
Q
22
¼ c
11
q
2
p
c
13
k
2
þ c
11
c
13
ðÞika
0
q
2
p
hi
K
n
q
p
R
þ
2c
66
q
p
R
1 þ ika
0
ðÞY
2
q
p
R
Q
23
¼
2c
66
nq
sh
R
Y
3
q
sh
RðÞ
Q
24
¼ c
11
q
2
sv
c
13
k
2
b
0
þ c
11
c
13
ðÞikq
2
sv
K
n
q
sv
RðÞ
þ
2c
66
q
sv
R
ik þ b
0
ðÞ
Y
2
q
sv
R
ðÞ
Q
31
¼ 0
Q
32
¼
2c
66
nq
p
R
1 þ ika
0
ðÞY
3
q
p
R
Q
33
¼c
66
q
2
sh
Y
4
q
sh
RðÞ
Q
34
¼
2c
66
nq
sv
R
ik þ b
0
ðÞY
3
q
sv
RðÞ
Q
42
¼c
44
q
p
2ik a
0
k
2
þ q
2
p
hi
Y
1
q
p
R
163 3.16 Waves in boreholes

Q
43
¼
iknc
44
R
K
n
q
sh
RðÞ
Q
44
¼ c
44
q
sv
k
2
þ q
2
sv
2ikb
0
Y
1
q
sv
RðÞ
a
0
¼
1
ik
c
13
þ 2c
44
ðÞk
2
c
11
q
2
p
o
2
c
44
k
2
c
11
c
13
c
44
ðÞq
2
p
o
2
b
0
¼ik
c
44
k
2
c
11
c
13
c
44
ðÞq
2
sv
o
2
c
13
þ 2c
44
ðÞk
2
c
11
q
2
sv
o
2
q
sh
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
c
44
k
2
o
2
c
66
s
q
p
¼ o
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
2
4UW
p
2U
s
q
sv
¼ o
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V
2
4UW
p
2U
s
f ¼ k
2
k
2
f
1=2
¼ radial wavenumber in the borehole fluid
k
f
¼ o=
f
¼ acoustic wavenumber in the borehole fluid
U ¼ c
11
c
44
V ¼ c
11
þ c
44
ðÞc
11
c
33
c
2
13
2c
13
c
44
k
2
=o
2
W ¼ c
33
c
44
=c
44
k
2
=o
2
=c
33
k
2
=o
2
where I
n
and K
n
are the modified Bessel functions of the first and second kind,
respectively, of order n. The azimuthal order number, n, controls the azimuthal
variations, with n ¼ 0, 1, and 2 corresponding to monopole, dipole, and quadrupole
modes, respectively. In the above expressions Y
i
denotes the same combinations of
modified Bessel functions as described for the isotropic case.
Isotropic, poroelastic, permeable formation
Borehole wave in permeable formations interacts with the formation permeability
through the propagation of Biot slow waves in the pore fluid. The Biot–Rosenbaum
theory (Rosenbaum, 1974) was the first to model monopole excitation in an open
borehole within an isotropic poroelastic formation. The theory was later extended to
transversely isotropic poroelastic formations with multipole excitations (Schmitt, 1989).
The Biot–Rosenbaum model solves the Biot poroelastic equations for a cylindrical
borehole geometry and boundary conditions. For the monopole case in an open
borehole of radius R, within a permeable formation, the dispersion relation is given
by (Tang and Cheng, 2004)
164 Seismic wave propagation
Dðo; kÞ¼
N
11
N
12
N
13
N
14
N
21
N
22
N
23
N
24
N
31
N
32
N
33
N
34
N
41
N
42
N
43
N
44
¼ 0
N
11
¼fI
1
fRðÞ
N
12
¼q
fast
1 þ b
fast
ðÞK
1
q
fast
RðÞ
N
13
¼q
slow
1 þ b
slow
ðÞK
1
q
slow
RðÞ
N
14
¼ik 1 þ b
s
ðÞK
1
q
s
RðÞ
N
21
¼
f
o
2
I
0
fRðÞ
N
22
¼2 q
2
fast
K
0
q
fast
RðÞþq
fast
K
1
q
fast
RðÞ=R
þ k
2
fast
l þ
þ b
fast
ðÞ
K
0
q
fast
RðÞ
N
23
¼2 q
2
slow
K
0
q
slow
RðÞþq
slow
K
1
q
slow
RðÞ=R
þ k
2
slow
l þ
þ b
slow
ðÞ
K
0
q
slow
RðÞ
N
24
¼ 2ik q
2
s
K
0
q
s
RðÞþq
s
K
1
q
s
RðÞ=R
N
31
¼ 0
N
32
¼2ikq
fast
K
1
q
fast
RðÞ
N
33
¼2ikq
slow
K
1
q
slow
RðÞ
N
34
¼ 2k
2
k
2
shear
q
s
K
1
q
s
RðÞ
N
41
¼
f
o
2
I
0
fRðÞ
N
42
¼ k
2
fast
þ b
fast
ðÞ=½K
0
q
fast
RðÞ
N
43
¼ k
2
slow
þ b
slow
ðÞ=½K
0
q
slow
RðÞ
N
44
¼ 0
where I
n
and K
n
are the modified Bessel functions of the first and second kind,
respectively, of order n, k is the axial wavenumber along the borehole axis, and o is
the angular frequency. The radial wavenumbers are given by
165 3.16 Waves in boreholes

q
fast
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
k
2
k
2
fast
q
q
slow
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
k
2
k
2
slow
q
q
s
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
k
2
k
2
shear
q
f ¼ k
2
k
2
f
1=2
¼ the radial wavenumber in the borehole fluid
k
f
¼ o =
f
¼ the acoustic wavenumber in the borehole fluid
k
fast
¼ k
p0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ b
fast
pf
=
1 b
fast
=b
0
s
k
slow
¼ k
p0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ b
slow
pf
=
1 b
slow
=b
0
s
k
p0
¼
o
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
l þ 2 þ
2
=ðÞ=
p
b
fast
slow
¼
1
2
c
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
c
2
4 1 cðÞ=b
0
p
hi
b
0
¼
l þ 2 þ
2
=ðÞ
c ¼
b
s
=
pf
b
0
þ b
s
b
s
¼
pf
o
2
k
shear
¼ o =
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
= þ
2
pf
o
2
r
¼ 1 K
dry
=K
m
¼ ðÞ=K
m
þ =K
pf
¼ 1 ðÞ
0
þ
pf
K
dry
¼ dry (drained) bulk modulus
l; ¼ Lame
´
constants of the dry (drained) porous formation
K
m
¼ mineral bulk modulus
r
0
¼ mineral density
K
pf
¼ pore fluid bulk modulus
pf
¼ pore fluid density
f ¼ porosity
¼ i oðÞ=o
¼ fluid viscosity
oðÞ¼dynamic permeability
166 Seismic wave propagation
