Михайлов В.С, Кудрявцев В.Г, Давыдов В.С. Навигация и лоция
Подождите немного. Документ загружается.

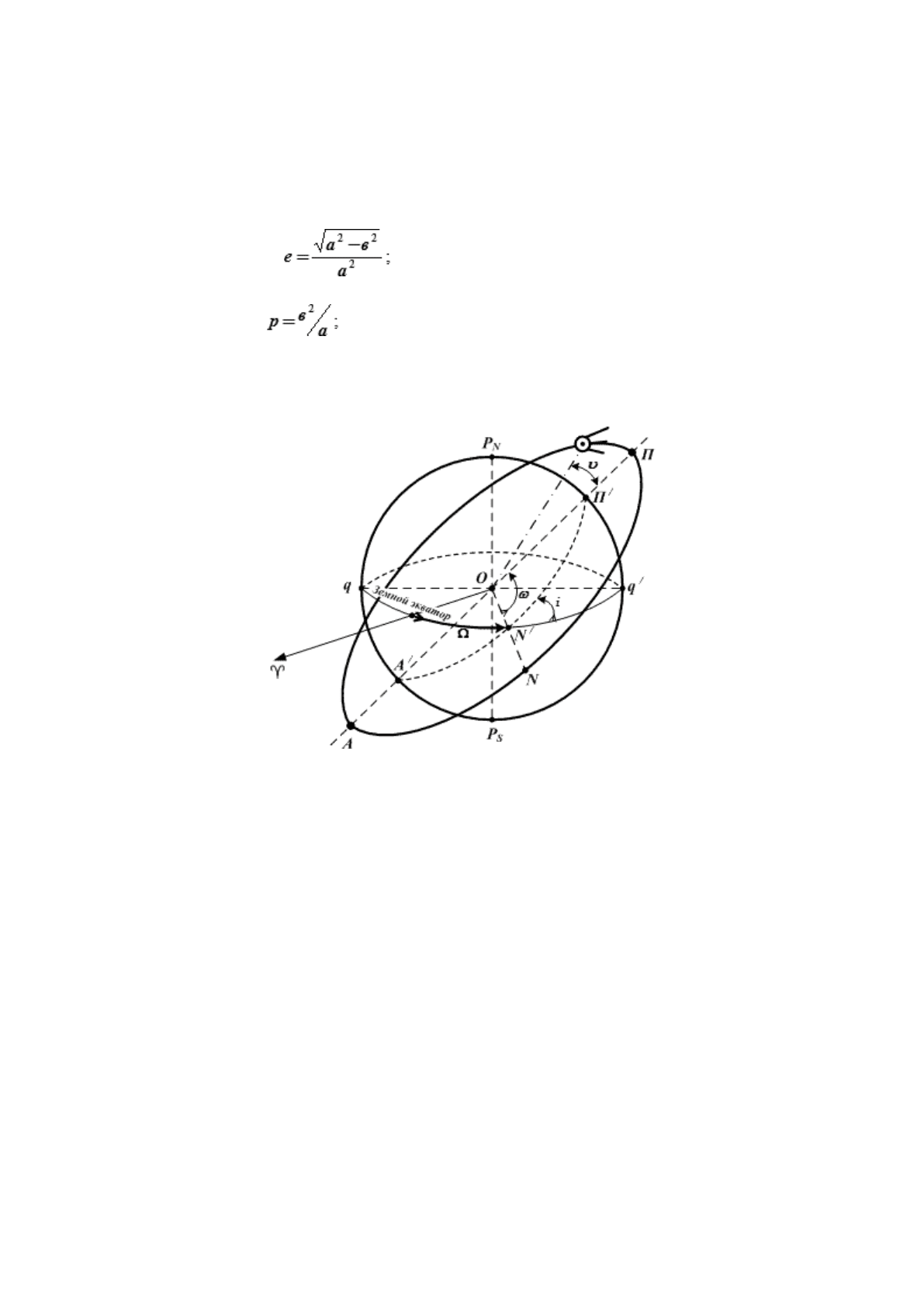
Эллиптическая орбита характеризуется 6-ю элементами Кеплера (рис. 23.1):
1. → наклонение плоскости орбиты к плоскости экватора (i) → угол между плоскостью земного
экватора и плоскостью орбиты ИСЗ;
2. → прямое восхождение восходящего узла орбиты (Ω) → угол между направлениями на точку
Овна и восходящий узел орбиты ИСЗ;
3. → угловое расстояние перигея от восходящего узла орбиты N (ω) → угол между направлениями
на восходящий узел орбиты ИСЗ и точку его перигея;
4. → эксцентриситет орбиты (е):
(23.7)
5. → параметр орбиты:
(23.8)
6. → время прохождения ИСЗ через перигей (П) или восходящий (N) узел (τ).
Элементы №№ 1÷5 характеризуют пространственное положение орбиты ИСЗ и направление его
движения.
Элемент № 6 (τ) – характеризует положение ИСЗ на орбите.
Рис. 23.1. Характеристика эллиптической орбиты ИСЗ
Для определения места судна по ИСЗ необходимо знать его координаты в момент наблюдений.
По известным значениям параметров орбиты ИСЗ можно вычислить его пространственные
координаты и положение его относительно земной поверхности на любой момент времени.
Мгновенное положение ИСЗ относительной земной поверхности можно определить длиной
радиуса-вектора его орбиты
ρ
0
= R + H
(23.9)
и координатами геозенита – точки на земной поверхности, для которой ИСЗ в данный момент
находится в зените.
В геометрической интерпретации именно точка геозенита является опорным пунктом,
относительно которого определяются навигационные параметры.
Вследствие того, что Земля не шар, а геоид и того, что на ИСЗ влияет ряд возмущающих сил
(сопротивление атмосферы Земли, притяжение Луны и Солнца, давление солнечной радиации,
магнитное поле Земли), кеплеровские элементы орбиты ИСЗ непрерывно изменяются.
Для исключения этого на все суда, использующие ИСЗ, сообщаются не только начальные
параметры элементов Кеплера, но и действительные поправки к ним (орбитальная информация).
23.1.2. Орбиты ИСЗ и их особенности
Орбита ИСЗ – это траектория его движения относительно центра Земли. Плоскость орбиты всегда
проходит через центр Земли.
Орбиты ИСЗ классифицируются по 2-м признакам:
1. По наклонению плоскости орбиты относительно плоскости экватора:
• экваториальные (i = 0° или i = 180°);
• полярные (i = 90°);
• наклонные (0°< i < 90°; 90°< i < 180°).
2. По высоте орбиты над земной поверхностью:
• низкие (Н < 5.000 км);
• средние (5.000 км < Н < 22.000 км);
• высокие (Н > 22.000 км).
Синхронный суточный ИСЗ, выведенный на экваториальную орбиту, будет неподвижно «висеть»
над определенной точкой земной поверхности. Такой ИСЗ – стационарный, так как его период Т = 23ч
56м 04с, то есть соответствует длительности звездных суток.
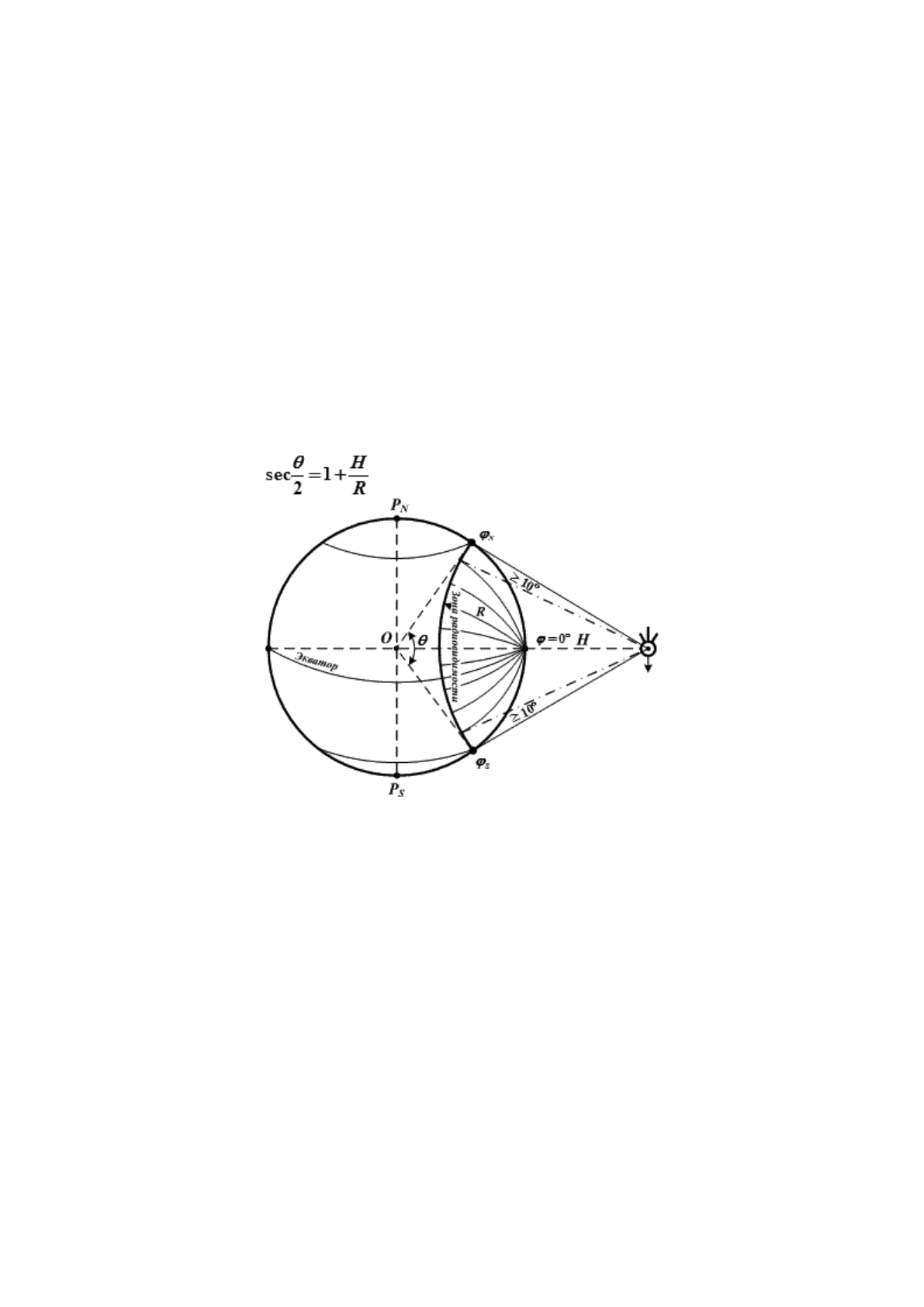
Малый круг на Земле, в пределах которого могут приниматься радиосигналы ИСЗ, называется
зоной радиовидимости (рис. 23.2). Сферический диаметр (θ) этой зоны определяется по формуле:
(23.10)
Рис. 23.2. Зона радиовидимости ИСЗ
Для стационарного ИСЗ при Н = 35.870 км, R
З
= 6.371 км, θ = 162°. Это означает, что такой ИСЗ на
экваториальной орбите будет теоретически видим до широты 81°N ≥ φ ≤ 81°S.
Для надежного приема сигналов необходимо, чтобы ИСЗ имел высоту не <10° над горизонтом (при
меньшей высоте – высок уровень помех и большое затухание радиоволн в атмосфере).
Стационарные ИСЗ пока не нашли применения в навигации (широко применяются для радиосвязи
и телевидения).
Для низкоорбитального ИСЗ (Н = 1.000 км) диаметр зоны видимости составляет 3.630 миль (θ ≈
60,5°).
При условии наблюдения такого ИСЗ при высоте >10° получаем диаметр зоны радиовидимости ≈
3.000 миль, что соответствует ширине Атлантического океана в самой широкой его части. То есть один
ИСЗ на полярной орбите, пролетая над серединой Атлантического океана, может наблюдаться во всех
его точках.
Так как ИСЗ движется относительно Земли, то будет перемещаться и зона радиовидимости, образуя
на поверхности Земли полосу радиовидимости.
Из-за вращения Земли полоса радиовидимости, соответствующая каждому последующему витку,
будет смещаться к западу на расстояние, определяемое по формуле:
d = 15 · sini · cosφ · T (миль)
(23.11)

Для ИСЗ (Н = 1000 км, Т = 106 мин.) получим для φ = 0°, что d = 1.575 миль (для φ = 60° d = 788
миль). Смещение полосы радиовидимости меньше ширины полосы, то есть на каждом последующем
витке будет иметь место перекрытие полос. Это перекрытие составляет: для φ = 0° ≈ 57%; для φ > 60° ≈
78%; для φ = 90° = 100%.
Это означает, что один и тот же ИСЗ на полярной орбите может наблюдаться в одном и том же
месте несколько раз подряд, то есть по одному ИСЗ в средних широтах можно определить место 4 раза
в сутки.
При Н = 1000 км суточное число оборотов ИСЗ соответствует ≈ 14. Следовательно, один ИСЗ на
полярной орбите может в течении суток обеспечить определение места во всех точках Земли, но таких
обсерваций будет мало и они будут редки.
Для обеспечения дискретности определений места судна в 1 час необходимо 6 ИСЗ на полярной
орбите (Н = 1000 км, Т = 106 мин., θ = 50°).
Большое значение для использования ИСЗ имеет продолжительность его наблюдения. Для
неподвижного наблюдателя, находящегося в плоскости орбиты ИСЗ продолжительность его
наблюдения максимальна.
(23.12)
Для ИСЗ с Н = 1.000 км и Т = 106 мин. ΔТ
Иmax
= 18 мин. (не > 16 мин.).
23.2. Особенности навигационного использования ИСЗ (НКА)
Использование ИСЗ (далее НКА – навигационный космический аппарат) в качестве подвижных
опорных станций спутниковой навигационной системы (СНС) открывает широкие возможности для
решения навигационной задачи определения места судна в море.
Однако, применение быстро перемещающихся в пространстве опорных станций для
навигационных целей, возможно лишь в том случае, если пространственные координаты этих станций
(НКА) относительно земной поверхности в момент измерения навигационных параметров известны с
необходимой точностью.
Это условие может быть выполнено при соблюдении двух условий:
1. → если известны уравнения движения НКА в функции времени и время, прошедшее с момента,
когда координаты НКА были известны, до момента их измерений на судне;
2. → если одновременно с радионавигационными сигналами НКА НКА излучают и сигналы,
несущие информацию о его фактических координатах.
Радионавигационные параметры определяются сравнением заранее предвычисленных (на
основании законов движения НКА) с измеренными.
При круговой орбите НКА предвычисленные значения определяемых радионавигационных
параметров можно получить по формулам сферической тригонометрии (рис. 23.3) из параллактического
треугольника спутника ZCP
N
в котором:
• А – азимут НКА;
• δ – склонение НКА;
• φ – широта места судна на время замера радионавигационных параметров;
• Z = 90° – h – зенитное расстояние НКА;
• t
M
– местный часовой угол НКА.
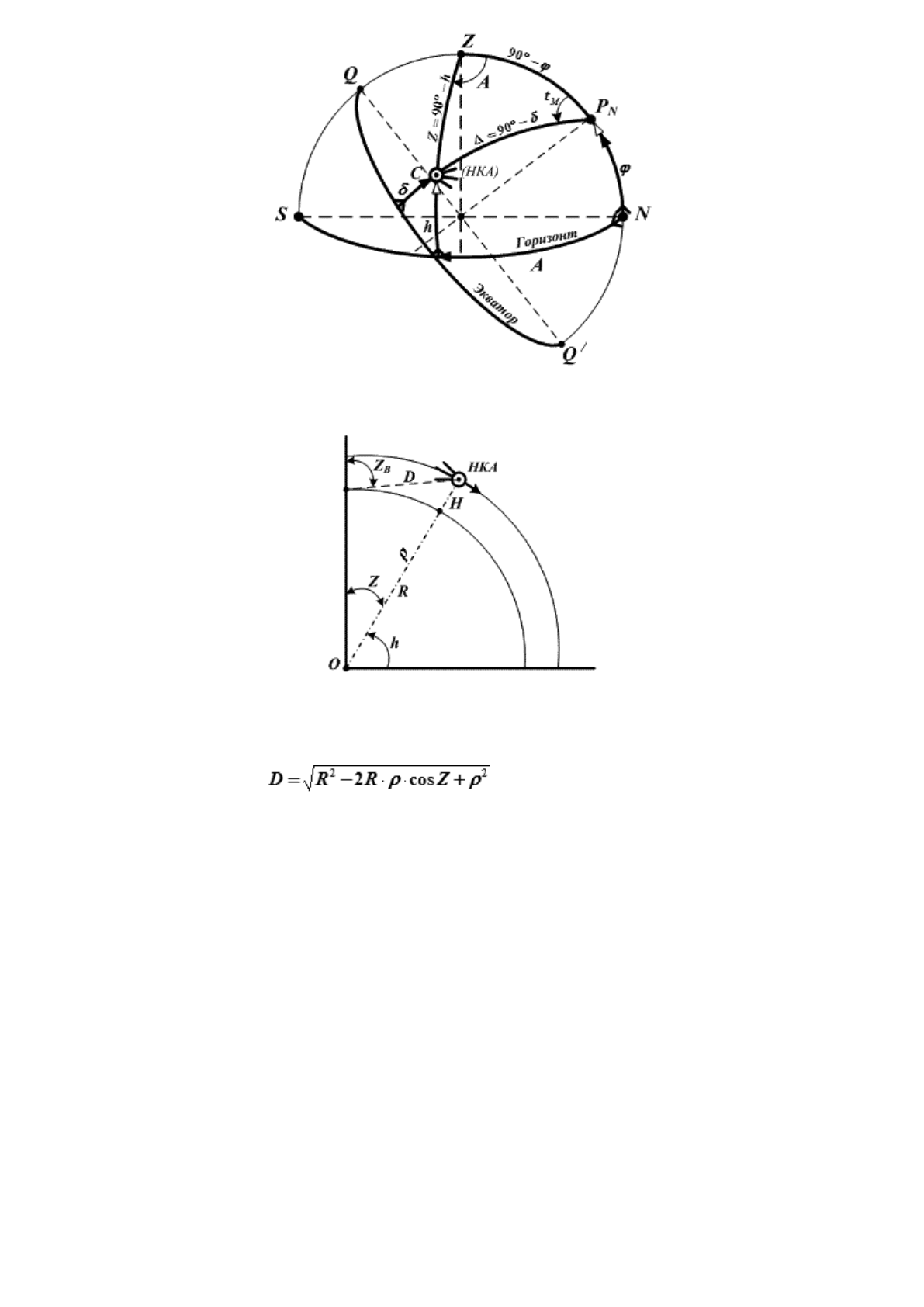
Рис. 23.3. Параллактический треугольник НКА
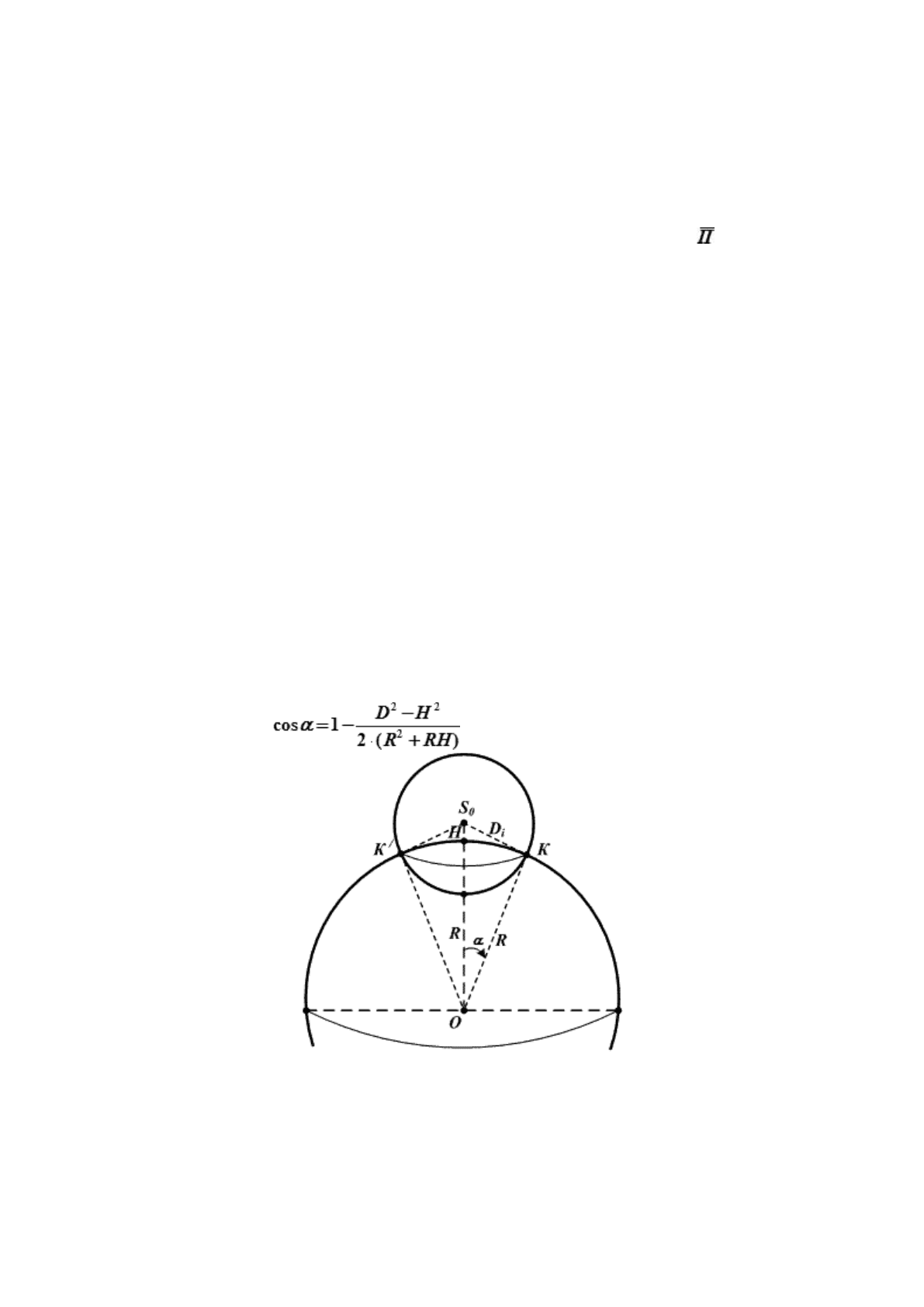
Рис. 23.4. Зенитное расстояние НКА
Расстояние до НКА (D) находится из соотношения:
(23.13)
где
cosZ = sinδ · sinφ + cosδ · cosφ · cost
M
Движение НКА в первом приближении подчиняется законам Кеплера. Однако, вследствие
сопротивления атмосферы и влияния аномалий гравитационного поля Земли фактическое движение
НКА по своей орбите отклоняется от расчетного, поэтому необходимо систематически наблюдать за
движением НКА с Земли и своевременно вносить поправки в информацию о его фактических
пространственных координатах.
Одновременно с этой информацией должна передаваться информация, позволяющая привести
наблюдения за движением НКА на наземных пунктах и навигационные определения по этим НКА к
единой системе времени.
Следовательно, необходимым элементом СНС, основанной на использовании НКА, является
комплекс наземных станций, наблюдающих за движением НКА, входящих в эту СНС, обеспечивающих
информацию об их движении и привязку всех измерений в едином для всей системы времени. Этот
комплекс называется наземным контрольно-измерительным комплексом (КИК).
Таким образом, использование НКА в качестве подвижных опорных станций не исключает и
наземные опорные станции, координаты которых определены очень точно.
Далее предполагается, что на судне имеется информация о параметрах движения НКА по орбите и
известно время, к которому отнесена эта информация.
Для судна одна поверхность положения (высота) всегда известна. Поэтому определение места
судна по НКА сводится к отысканию точки пересечения линий положения на поверхности
земного сфероида.
Существенное значение для работы СНС, основанной на использовании НКА, имеет большая
скорость изменения радионавигационных параметров, определяемых при помощи этой системы,
позволяющая применять методы навигационных определений, основанные на измерениях скорости и
ускорения сближения НКА и судна. Эти методы осуществляются посредством наблюдения за
приращением частоты принимаемых от НКА сигналов, возникающих вследствие эффекта Доплера.
Одной из особенностей навигационного использования НКА, обусловливаемой своеобразным
характером его движения относительно земной поверхности, является различие условий
геометрической видимости НКА на различных широтах в зависимости от параметров орбиты.
23.3. Способы радионавигационных определений по НКА
Условия навигационных определений с движущегося судна относительно подвижной или
неподвижной опорной станции различаются между собой только скоростью изменения навигационных
параметров, определяемых относительно опорных станций.
Вследствие этого навигационное определение при помощи НКА можно производить теми же
способами, что и при использовании РНС с неподвижными опорными станциями.
Однако, большие скорости изменения навигационных параметров:
1. исключают возможность неавтоматических или полуавтоматических измерений;
2. резко повышают требования к скорости отработки следящих систем судовых
приемоиндикаторов;
3. создают возможность эффективного использования скоростных методов определения линий
положения.
С учетом перечисленных особенностей при помощи НКА можно определять место судна в море,
измеряя:
• расстояния до НКА;
• направления на НКА в горизонтной системе координат;
• разности расстояний до нескольких последовательных положений НКА на орбите;
• скорость и ускорение сближения с НКА.
Расстояния до НКА можно измерять способами: 1) «запрос-ответ» и 2) с помощью «двух
генераторов».
Определение направлений, то есть высоты (зенитного расстояния) и азимута на НКА,
методически не отличается от определения направлений на небесные светила.
Разность расстояний до нескольких последовательных положений НКА можно получить, измеряя
величину угла изменения фазы принимаемого сигнала, за счет изменения длины пути, проходимого
этим сигналом между НКА и судном.
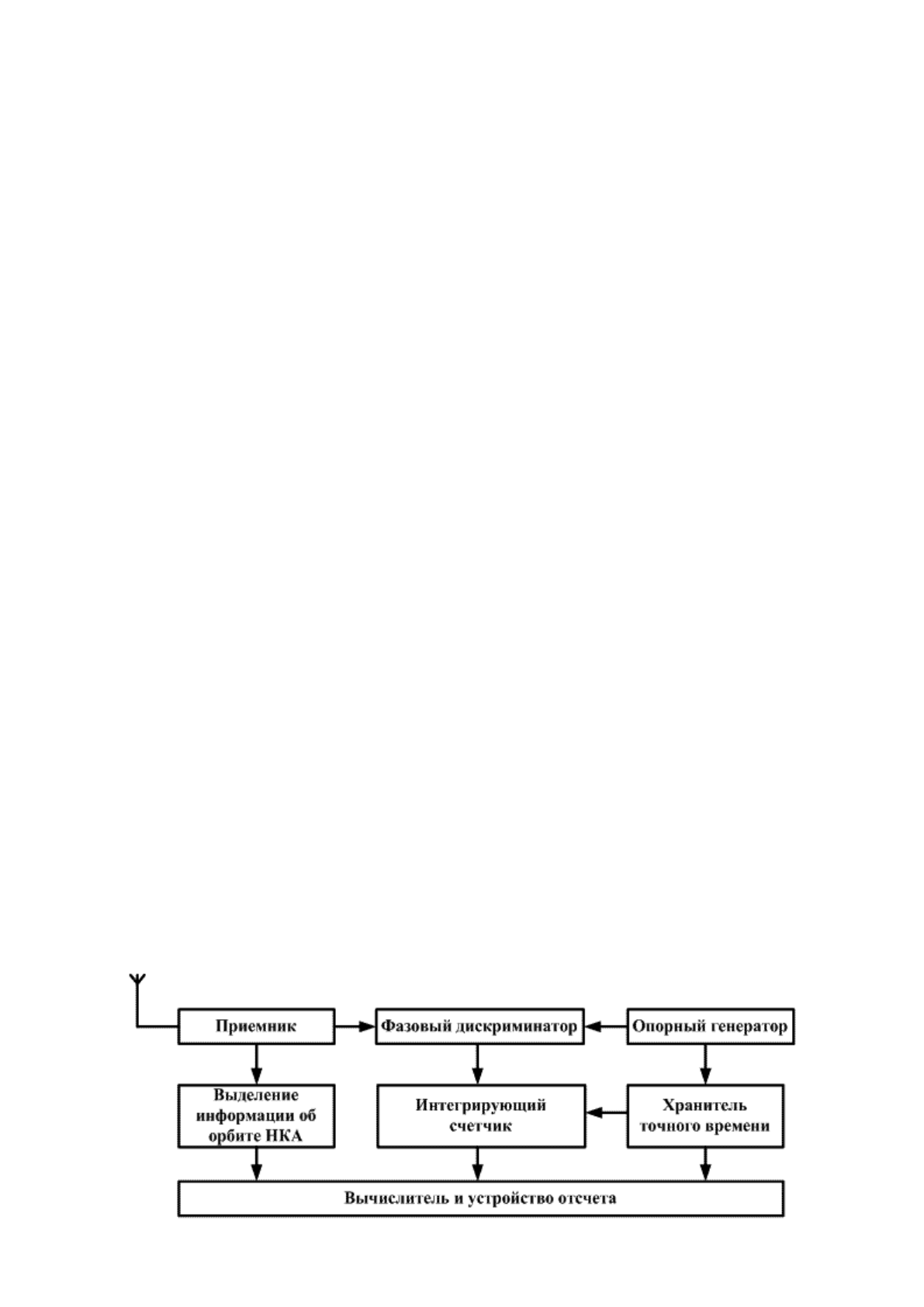
Такое измерение можно осуществить по блок-схеме (рис. 23.5) путем непрерывного сравнения
частоты колебаний, принимаемых от НКА, с частотой колебаний опорного генератора и
интегрирования набега фазы за счет эффекта Доплера.
Рис. 23.5. Блок-схема доплеровского метода определения линии положения
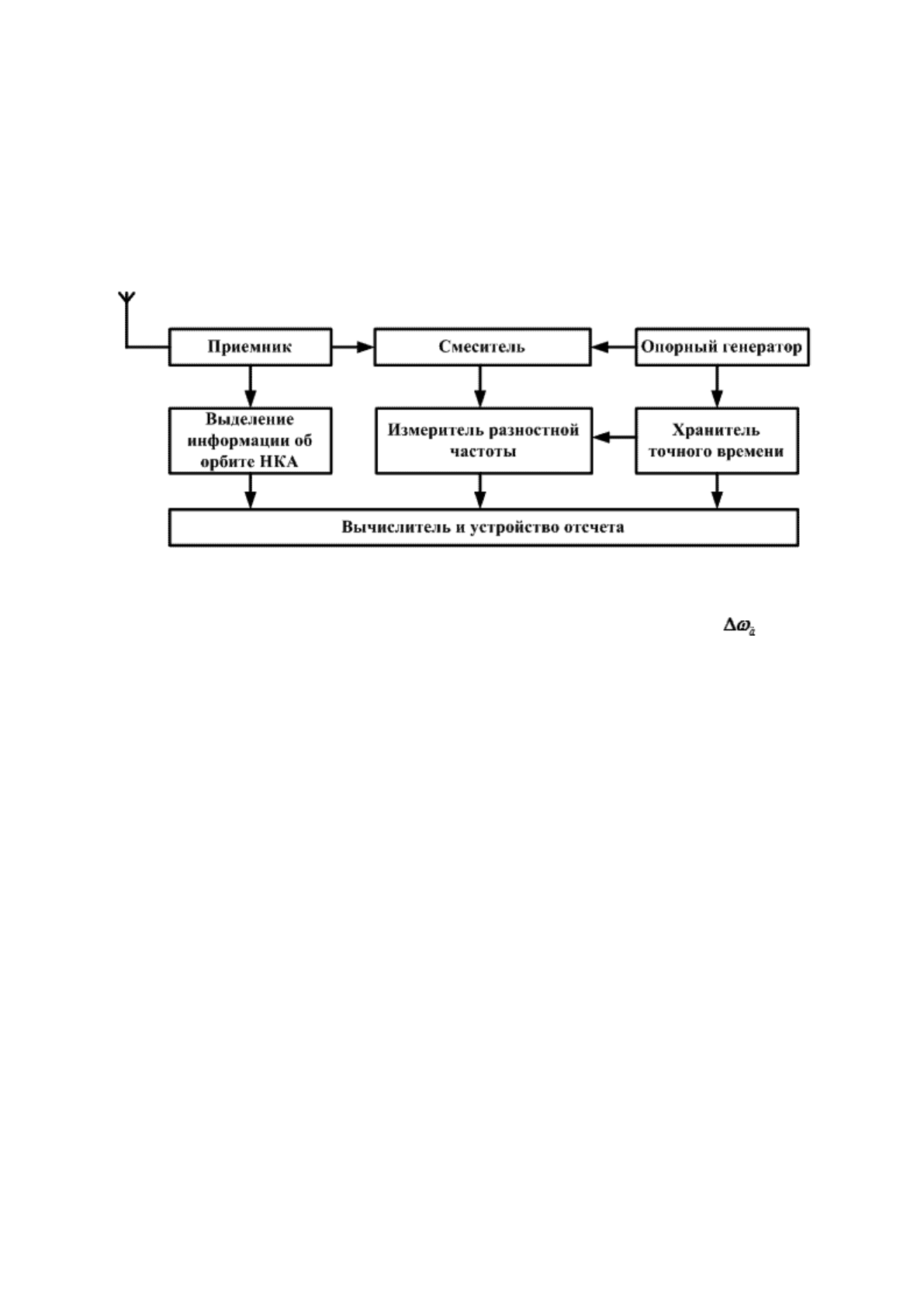
Основным условием выполнения измерений по этой схеме является равенство частоты (ω
И
)
колебаний, излучаемых с НКА и частоты (ω
0
) колебаний опорного генератора.
Хотя доплеровское приращение частоты принимаемых колебаний здесь непосредственно не
измеряется, а используется лишь для измерения суммарного сдвига фаз сравниваемых колебаний,
рассмотренный фазовый метод определения разности расстояний до НКА часто называют
доплеровским методом.
Доплеровский метод определения линии положения при помощи НКА можно осуществить двумя
основными способами: 1) дифференциальным и 2) траверзным.
Дифференциальный способ измерения скорости сближения сводится к прямому измерению
мгновенных значений разности частот принимаемых колебаний и колебаний местного опорного
генератора (рис. 23.6).
Рис. 23.6. Блок-схема дифференциального способа измерения скорости сближения с НКА
Если частота ω
И
= ω
0
, то величина доплеровского приращения частоты при известных
значениях ω
И
и υ
Ф
определяет значение производной dD / dt, то есть скорость сближения НКА и судна.
Траверзный способ измерения ускорения сближения с НКА осуществляется путем определения
момента прохождения доплеровского приращения частоты (Δ ω
д
) через нуль и сводится к измерению
скорости изменения частоты в этот момент.
Так как в момент, когда Δω
д
= 0, судно находится на траверзе орбиты НКА, этот способ и называют
траверзным.
Измеренное значение скорости изменения частоты определяет вторую производную от расстояния
до НКА по времени, то есть ускорение сближения НКА и судна.
Траверзным способом определения координат места судна за одно прохождение НКА можно
получить всего лишь две линии положения, пересекающихся под углом 90°.
Малое количество получаемой информации является наиболее существенным недостатком
траверзного способа. Однако этот недостаток компенсируется более простой обработкой получаемой
информации, что позволяет определять место судна по НКА без специальной судовой ЭВМ.
23.4. Методы определения места судна по НКА
Основным содержанием навигационной задачи, решаемой с помощью навигационной аппаратуры
потребителя (НАП), является определение пространственно-временны´х координат подвижного объекта
(судна), а также составляющих его скорости. В результате решения навигационной задачи должен быть
определен вектор состояния судна.
Непосредственно измерить элементы вектора состояния не представляется возможным. У
принятого с НКА радиосигнала определяют отдельные его параметры (например, задержку или
доплеровский сдвиг частоты). Поэтому измеряемый в интересах навигации параметр радиосигнала
называют радионавигационным, а соответствующий ему геометрический параметр –
навигационным. Например, задержка радиосигнала и его доплеровское смещение частоты (f
ДОП
)
являются радионавигационными параметрами, а соответствующие им дальность до судна (D) и
радиальная скорость сближения (V
ρ
) – навигационными параметрами.
Геометрическое место точек пространства с одинаковым значением навигационного параметра
называется поверхностью положения.
Пересечение двух поверхностей положения определяет линию положения – геометрическое место
точек, имеющих два определенных значения двух навигационных параметров.
Местоположение судна определяется координатами трех поверхностей положения или двух линий
положения. Иногда (из-за нелинейности) две линии положения могут пересекаться в двух точках.
Тогда, для нахождения места судна, необходимо использовать дополнительную поверхность положения
или другую информацию о его месте.
Для решения навигационной задачи используют функциональную зависимость между
навигационными параметрами и компонентами вектора состояния судна . Соответствующие
функциональные зависимости называются навигационными функциями.
Навигационные функции получают различными методами, основные из которых:
• дальномерный (А);
• псевдодальномерный (Б);
• разностно-дальномерный (В);
• радиально-скоростной (Г).
Могут быть использованы и другие методы и их комбинации, в том числе и для определения
ориентации судна.
А. Дальномерный метод
Дальномерный метод основан на пассивных (беззапросных) измерениях дальности (D
i
) между i-ым
НКА и судном. Навигационным параметром является дальность (D
i
), а поверхностью положения –
сфера с радиусом D
i
и центром, расположенным в центре масс i-го НКА.
При пересечении сферической изоповерхности с поверхностью Земли получим изолинию,
соответствующую измеренной дальности до НКА – окружность сферического радиуса α.
Из треугольника S
0
ОК (рис. 23.7):
D
i
2
= R
2
+ (R + H)
2
− 2R · (R + H) · cosα
(23.14)
или
(23.15)
Рис. 23.7. Дальномерный метод получения навигационной функции
Градиент этой изолинии:
g = cosh
ρ
(23.16)
где h
ρ
– видимая угловая высота НКА над горизонтом.
Топоцентрическая дальность (D
i
) может быть измерена пассивным или активным методами.
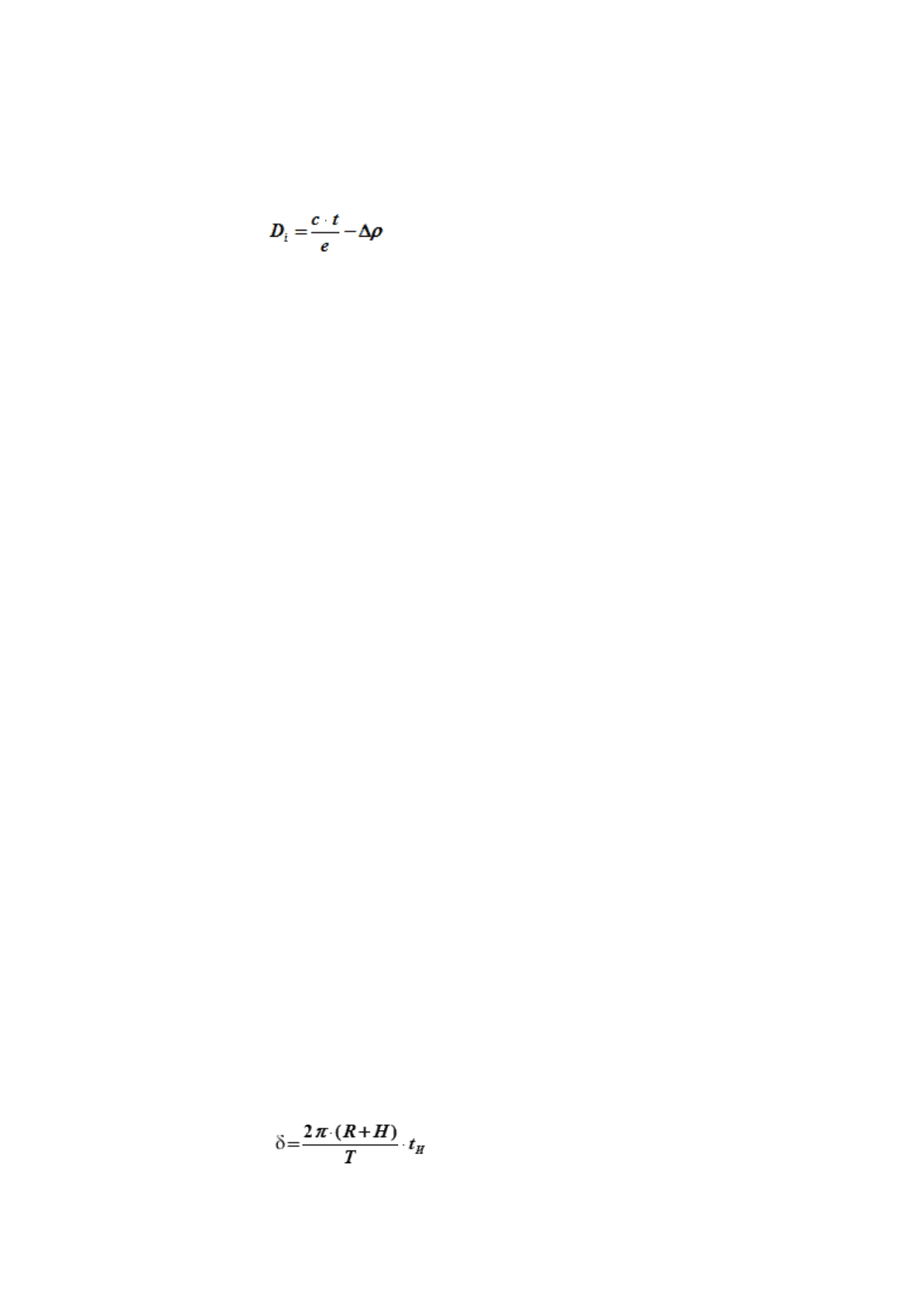
Пассивный метод состоит в определении D
i
по времени (t) распространения радиосигнала от НКА
до приемника (судна):
D
i
= c · (t + δ
t
)
(23.17)
где δ
t
– поправка к отсчету времени (t) из-за сдвига временных шкал часов НКА и судового приемника.
Для измерения дальности D
i
пассивным методом с высокой точностью – на НКА и на судне
должны быть высокостабильные генераторы частоты.
Активный метод измерения дальности до НКА аналогичен методу измерения расстояния до
активного радиолокационного отражателя
(23.18)
Этот метод не требует наличия высокостабильных генераторов частоты на судне. Но в этом методе
другая проблема – обеспечение одновременного обслуживания сотен и тысяч потребителей.
Дальномерный пассивный метод применяется в СНС на средневысоких орбитах GPS (США) и
ГЛОНАСС (РФ).
Место судна определяют как координаты точки пересечения трех поверхностей положения (трех
сфер), вследствие чего для реализации этого метода необходимо измерить дальности до 3-х НКА.
Неоднозначность определения координат судна при этом методе устраняется с помощью
дополнительной информации (счислимые координаты судна, его радиальная скорость и др.).
Дальномерный метод предполагает, что все измерения дальностей должны быть произведены в
одно время. Однако координаты НКА привязаны к бортовой шкале времени, а координаты судна
определены в своей шкале. В реальных условиях существует расхождение (t′) этих шкал времени и
возникает смещение (D′ = c · t′) измеренной дальности относительно истинной, поэтому точность
определения места судна падает. Таким образом, недостатком метода является необходимость
высокоточной привязки шкал времени НКА и судна, вследствие чего в настоящее время более широкое
применение нашел псевдодальномерный метод определения места.
Б. Псевдодальномерный метод
Под псевдодальностью от i-го НКА до подвижного объекта понимают измеренную дальность
(D
ИЗМi
) до этого спутника, отличающуюся от истинной дальности (D
i
) на неизвестную, но постоянную за
время определения навигационных параметров величину (D′).
В этом методе в качестве навигационного параметра принята D
ИЗМi
. Поверхностью положения
является сфера с центром в точке центра масс НКА. При этом радиус сферы изменен на неизвестную
величину D′. Измерение псевдодальностей до трех НКА приводит к системе трех уравнений с четырьмя
неизвестными (х, у, z, D′ ), что вызывает неопределенность ее решения. Для устранения
неопределенности необходимо провести дополнительное измерение псевдодальности до четвертого
НКА и получить точное решение системы уравнений, то есть получить место подвижного объекта как
точку пересечения четырех поверхностей положения.
Необходимость нахождения в зоне радиовидимости четырех НКА предъявляет жесткие требования
к структуре орбитальной группировки НКА, которые могут быть выполнены только в
среднеорбитальных СНС.
Достоинством данного метода является то, что он не накладывает жестких ограничений на
значение погрешности D′ = c · t′ (погрешности временной шкалы) и позволяет дополнительно
вычислять отклонение шкалы времени подвижного объекта.
В. Разностно-дальномерный метод (доплеровский интегральный)
Этот метод основан на измерении разности топоцентрических расстояний между судном и двумя
положениями одного и того же НКА в последовательные моменты времени.
В своем движении по орбите НКА последовательно проходит точки S
1
, S
2
и т.д. расстояние между
которыми называется базой, длина которой определяется как:
(23.19)
где
t
И
– время интегрирования – промежуток времени между двумя последовательными моментами
наблюдения НКА.

Если измерить разность расстояний
ΔD
1
= D
i2
− D
i1
(23.20)
двух последовательных положений НКА, то место наблюдателя окажется на изоповерхности,
представляющей собой гиперболоид вращения, фокусы которого совпадают с концами базы, то есть
положениями НКА на орбите в моменты начала и конца наблюдений. Гиперболоид образован
вращением гиперболы, соответствующей измеренной разности расстояний ΔD вокруг базы и является
поверхностью второго порядка.
Пересечение гиперболоида с поверхностью Земли дает изолинию – сложную кривую, близкую по
форме к сферической гиперболе. На этой гиперболе и будет находиться судно.
Когда база займет новое положение измеряют вторую разность расстояний
ΔD
2
= D
i3
− D
i2
(23.21)
и получают второй гиперболоид и вторую гиперболу, соответствующую величине ΔD
2
.
Аналогично можно получить ΔD
3
и третью гиперболу и т.д. Место судна получается в точке
пересечения 2-х , 3-х и более гипербол.
Разность расстояний ΔD
i
можно получить подсчетом числа импульсов доплеровской частоты в
течении промежутка времени, необходимого НКА для прохождения длины базы. Такой подсчет
математически представляет собой интегрирование доплеровского смещения частоты по времени, в
результате которого получаем:
(23.22)
где N
σ
– подсчитанное число импульсов биений доплеровской частоты.
Таким образом, каждому N
σ
соответствует вполне определенное значение разности расстояний от
судна до двух последовательных положений НКА на орбите в моменты начала и конца времени t
И
–
интервала интегрирования.
Постоянная величина δ
t
· t
И
– погрешность в определении числа импульсов биений из-за сдвига
частоты опорного генератора судового приемоиндикатора.
В этом методе спутниковая РНС аналогична наземной гиперболической РНС.
В судовом ПИ спутниковой РНС «Транзит» были приняты t
И
= 2 мин., 1 мин., 30с, 24с. При ΔТ
Иmax
= 16 мин. может быть получено соответственно 8, 16, 32 и 40 линий положения.
Так как гиперболы на поверхности Земли пересекаются в двух точках, то определение места судна
будет двузначным и разрешение этой двузначности выполняются по счислению пути судна.
В состав судового ПИ входит ЭВМ, так как получаемая от НКА информация не может быть
обработана вручную.
В среднеорбитальных СНС при этом методе используются три разности ΔD
ij
= D
i
− D
j
до 4-х НКА,
так как при постоянстве D′ за время навигационных определений разности псевдодальностей равны
разностям истинных дальностей, для определения которых требуется только три независимых
уравнения.
Навигационным параметром является Δ D
ij
. Поверхности положения представляют собой
поверхности двухполостного гиперболоида вращения, фокусами которого являются координаты
опорных точек i и j (центров масс i-го и j-го НКА). Расстояние между этими опорными точками
называется базой. Если расстояния от опорных точек (НКА) до подвижного объекта велики по
сравнению с базой, то гиперболоид вращения в окрестностях точки подвижного объекта совпадает со
своей асимптотой – конусом, вершиной которого выступает середина базы.
Точность определения места подвижного объекта совпадает с точностью определения этих
координат псевдодальномерным способом.
Недостаток разностно-дальномерного метода заключается в том, что в нем не может быть измерено
смещение D′, то есть смещение шкалы времени подвижного объекта.
Г. Радиально-скоростной (доплеровский дифференциальный) метод
Быстрое перемещение НКА в зоне радиовидимости наблюдателя позволяет применять этот метод,
основанный на измерении радиальной скорости, то есть скорости сближения НКА с наблюдателем
(судном). Для измерения радиальной скорости используется эффект Доплера, сущность которого
заключается в том, что при быстром перемещении НКА, излучающего колебания строго определенной
частоты f
0
, наблюдатель на Земле (на судне) будет принимать колебания другой частоты f.
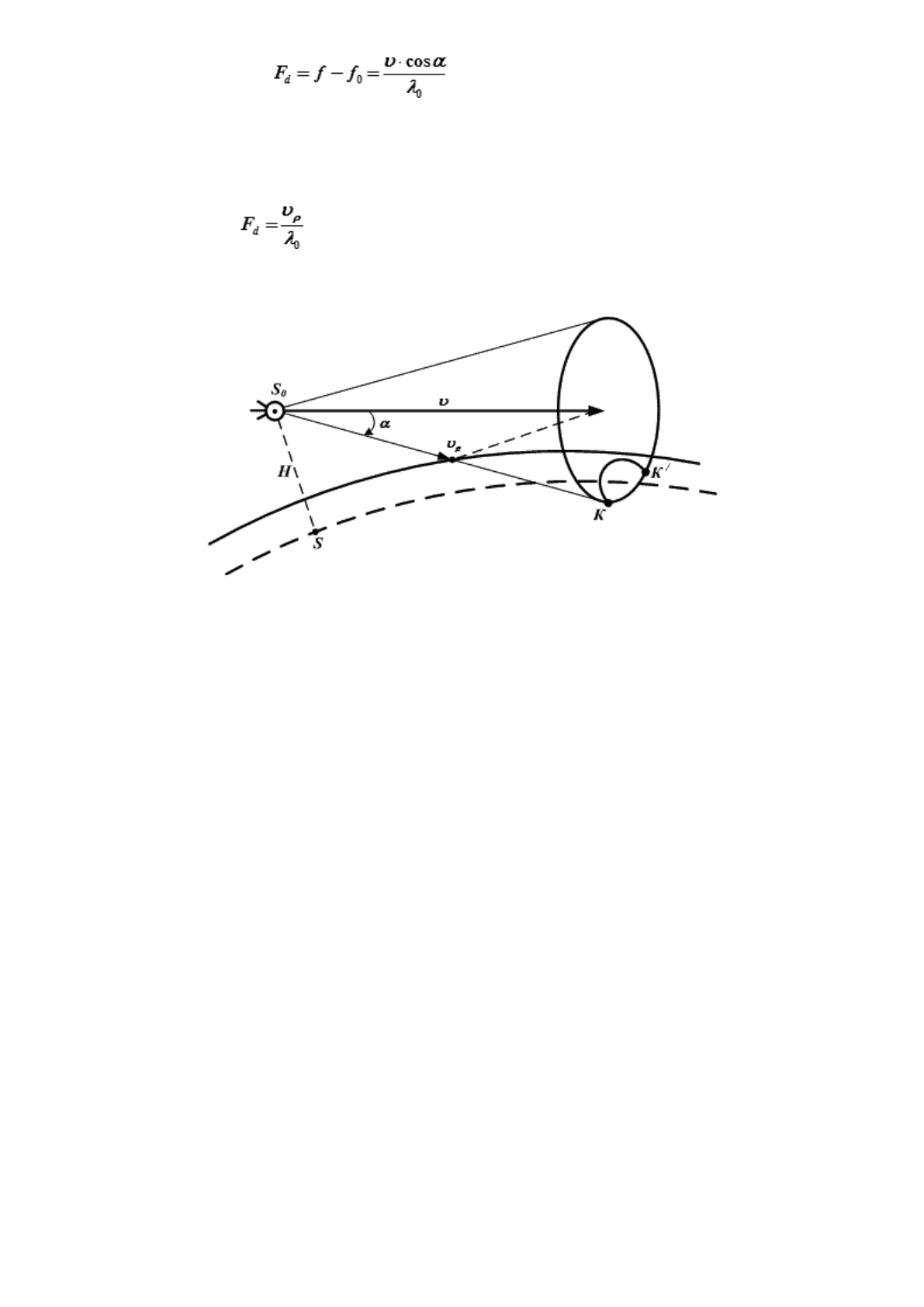
Разность этих колебаний, называемая доплеровским смещением частоты, определяется по формуле:
(23.23)
где
υ – скорость движения НКА по орбите;
α – направление на судно с НКА;
λ
0
– длина волны, соответствующая частоте f
0
.
Так как υ · cosα = υ
ρ
– радиальная скорость НКА, то
(23.24)
Если F
d
= const, то α = const и υ
ρ
= const. Углу α = const в пространстве соответствует
изоповерхность в виде кругового конуса, вершина которого совпадает с местом НКА, а ось – с вектором
его скорости (рис. 23.8).
Рис. 23.8. Радиально-скоростной метод получения навигационной функции
Так как судно находится на Земле, то его место надо искать на кривой КК′, по которой конус
пересекается с поверхностью Земли. Эта кривая – изодопа – изолиния на поверхности Земли,
характеризующаяся постоянством доплеровского смещения частоты и постоянством радиальной
скорости НКА.
Изодопа по своей форме близка к сферической гиперболе.
Перемещение НКА приводит к перемещению изодоп. Точка их пересечения – место судна. Для
определения места судна требуется несколько изолиний – изодоп. Вторую и последующие изодопы
получают вскоре после первой.
Изодопы пересекаются в двух точках (т. К и т. К′) лежащих по разные стороны трассы НКА.
Подобная двузначность разрешается с помощью счисления пути судна.
За время пролета низкоорбитальных НКА может быть получено несколько сотен изодоп (при
ΔТ
Иmax
= 16 мин. = 960 изодоп, а при измерении доплеровского смещения частоты за 4 мин. может быть
получено 240 изодоп).
В среднеорбитальных СНС этот метод базируется на измерении трех радиальных скоростей
подвижного объекта относительно трех НКА. В основу метода положена зависимость радиальной
скорости точки относительно НКА от координат и относительной скорости спутника.
Недостатком этого метода является невозможность проведения измерений в реальном времени.
Кроме того, в среднеорбитальных СНС реализация метода затруднена из-за медленного изменения
радиальной скорости. Это обусловило применение радиально-скоростного метода в среднеорбитальных
СНС только для определения составляющих скорости подвижного объекта. Однако для его реализации
необходим высокостабильный эталон частоты. Нестабильность последнего приводит к
неконтролируемому изменению доплеровского смещения частоты, что, в свою очередь, влечет
дополнительные погрешности измерения составляющих скорости подвижного объекта.
