Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


3.2 State-Space Process Models 67
3.2.1 Concept of State
Consider a continuous-time MIMO system with m input variables and r out-
put variables. The relation between input and output variables can be ex-
pressed as (see also Section 2.3)
dx(t)
dt
= f(x(t), u(t)) (3.39)
y(t)=g(x(t), u(t)) (3.40)
where x(t) is a vector of state-space variables, u(t) is a vector of input vari-
ables, and y(t) is a vector of output variables.
The state of a system at time t
0
is a minimum amount of information which
(in the absence of external excitation) is sufficient to determine uniquely the
evolution of the system for t ≥ t
0
.
If the vector x(t
0
) and the vector of input variables u(t)fort>t
0
are
known then this knowledge suffices to determine y(t),t>t
0
,thus
y(t
0
,t]=y{x(t
0
), u(t
0
,t]} (3.41)
where u(t
0
,t], y(t
0
,t] are vectors of input and output variables over the inter-
val (t
0
,t] respectively.
The above equation is equivalent to
x(t
0
,t]=x{x(t
0
), u(t
0
,t]} (3.42)
Therefore, the knowledge about the states at t = t
0
removes the necessity
to know the past behavior of the system in order to forecast its future and
the future evolution of states is dependent only on its present state and future
inputs.
This definition of state will be clearer when we introduce a solution of
state-space equation for the general functions of input variables.
3.2.2 Solution of State-Space Equations
Solution of state-space equations will be specified only for linear systems with
constant coefficients with the aid of Laplace transform techniques. Firstly, a
simple example will be given and then it will be generalised.
Example 3.4: Mixing process - solution of state-space equations
Consider a process of mixing shown in Fig. 3.4 with mathematical model
described by the equation
V
dc
1
dt
= qc
0
− qc
1
where c
0
,c
1
are concentrations with dimensions mass/volume, V is a con-
stant volume of the vessel, and q is a constant volumetric flow rate.

68 3 Analysis of Process Models
V
q
q
1
c
(
t
)
0
c
(
t
)
1
c
(
t
)
Fig. 3.4. A mixing process
In the steady-state holds
qc
s
0
− qc
s
1
=0
Introduce deviation variables
x = c
1
− c
s
1
u = c
0
− c
s
0
and define the process output variable y = x. Then the process state-space
equations are of the form
dx
dt
= ax + bu
y = cx
where a = −1/T
1
,b=1/T
1
,c=1.T
1
= V/q is the process time constant.
Assume that the system is at t
0
= 0 in the state x(0) = x
0
. Then the time
solution can be calculated by applying the Laplace transform:
sX(s) − x(0) = aX(s)+bU(s)
X(s)=
1
s −a
x(0) +
b
s −a
U(s)
The time domain description x(t) can be read from Table 3.1 for the first
term and from the convolution transformation for the second term and is
given as
x(t)=e
at
x(0) +
t
0
e
a(t−τ)
bu(τ)dτ
and for y(t)
y(t)=ce
at
x(0) + c
t
0
e
a(t−τ)
bu(τ)dτ
After substituting for the constants yields for y(t)
y(t)=e
−
q
V
t
x(0) +
V
q
t
0
e
−
q
V
(t−τ)
u(τ)dτ

3.2 State-Space Process Models 69
Solution of State-Space Equations for the Multivariable Case
The solution for the multivariable case is analogous as in the previous example.
Each state equation is transformed with the Laplace transform applied and
transformed back into the time domain. The procedure is simplified if we use
matrix notation.
Consider state-space equations
dx(t)
dt
= Ax(t)+Bu(t), x(0) = x
0
(3.43)
y(t)=Cx(t) (3.44)
Taking the Laplace transform yields
sX(s) − x
0
= AX(s)+BU(s) (3.45)
X(s)=(sI −A)
−1
x
0
+(sI −A)
−1
BU(s) (3.46)
and after the inverse transformation for x(t), y(t) hold
x(t)=e
At
x(0) +
t
0
e
A(t−τ)
BU(τ)dτ (3.47)
y(t)=Ce
At
x(0) + C
t
0
e
A(t−τ)
BU(τ)dτ (3.48)
e
At
= L
−1
(sI −A)
−1
(3.49)
The equation (3.48) shows some important properties and features. Its
solution consists of two parts: initial conditions term (zero-input response)
and input term dependent on u(t) (zero-state response).
The solution of (3.43) for free system (u(t)=0)is
x(t)=e
At
x(0) (3.50)
and the exponential term is defined as
e
At
=
∞
i=1
A
i
t
i
i!
(3.51)
The matrix
Φ(t)=e
At
= L
−1
(sI −A)
−1
(3.52)
is called the state transition matrix,(fundamental matrix, matrix exponential).
The solution of (3.43) for u(t) is then
x(t)=Φ(t −t
0
)x(t
0
) (3.53)
The matrix exponential satisfies the following identities:

70 3 Analysis of Process Models
x(t
0
)=Φ(t
0
− t
0
)x(t
0
) ⇒ Φ(0) = I (3.54)
x(t
2
)=Φ(t
2
− t
1
)x(t
1
) (3.55)
x(t
2
)=Φ(t
2
− t
1
)Φ(t
1
− t
0
)x(t
0
) (3.56)
The equation (3.52) shows that the system matrix A plays a crucial role in
the solution of state-space equations. Elements of this matrix depend on coef-
ficients of mass and heat transfer, activation energies, flow rates, etc. Solution
of the state-space equations is therefore influenced by physical and chemical
properties of processes.
The solution of state-space equations depends on roots of the character-
istic equation
det(sI −A) = 0 (3.57)
This will be clarified from the next example
Example 3.5: Calculation of matrix exponential
Consider a matrix
A =
−1 −1
0 −2
The matrix exponential corresponding to A is defined in equation (3.52)
as
Φ(t)=L
−1
$
s
10
01
−
−1 −1
0 −2
−1
%
= L
−1
$
s +1 1
0 s +2
−1
%
= L
−1
⎧
⎪
⎪
⎨
⎪
⎪
⎩
1
det
s +1 1
0 s +2
s +2 −1
0 s +1
⎫
⎪
⎪
⎬
⎪
⎪
⎭
= L
−1
1
(s+1)(s+2)
s +2 −1
0 s +1
= L
−1
1
s+1
−1
(s+1)(s+2)
0
1
s+2
The elements of Φ(t) are found from Table 3.1 as
Φ(t)=
e
−t
e
−2t
− e
−t
0e
−2t
3.2.3 Canonical Transformation
Eigenvalues of A, λ
1
,...,λ
n
are given as solutions of the equation

3.2 State-Space Process Models 71
det(A −λI) = 0 (3.58)
If the eigenvalues of A are distinct, then a nonsingular matrix T exists, such
that
Λ = T
−1
AT (3.59)
is an diagonal matrix of the form
Λ =
⎛
⎜
⎜
⎜
⎝
λ
1
0 ... 0
0 λ
2
... 0
.
.
.
.
.
.
00... λ
n
⎞
⎟
⎟
⎟
⎠
(3.60)
The canonical transformation (3.59) can be used for direct calculation of
e
−At
. Substituting A from (3.59) into the equation
dx(t)
dt
= Ax(t), x(0) = I (3.61)
gives
d(T
−1
x)
dt
= ΛT
−1
x, T
−1
x(0) = T
−1
(3.62)
Solution of the above equation is
T
−1
x =e
−Λt
T
−1
(3.63)
or
x = T e
−Λt
T
−1
(3.64)
and therefore
Φ(t)=T e
−Λt
T
−1
(3.65)
where
e
Λt
=
⎛
⎜
⎜
⎜
⎝
e
λ
1
t
0 ... 0
0e
λ
2
t
... 0
.
.
.
.
.
.
00...e
λ
n
t
⎞
⎟
⎟
⎟
⎠
(3.66)
3.2.4 Stability, Controllability, and Observability
of Continuous-Time Systems
Stability, controllability, and observability are basic properties of systems
closely related to state-space models. These properties can be utilised for
system analysis and synthesis.

72 3 Analysis of Process Models
Stability of Continuous-Time Systems
An important aspect of system behaviour is stability. System can be defined
as stable if its response to bounded inputs is also bounded. The concept of
stability is of great practical interest as nonstable control systems are unac-
ceptable. Stability can also be determined without an analytical solution of
process equations which is important for nonlinear systems.
Consider a system
dx(t)
dt
= f(x(t), u(t),t), x(t
0
)=x
0
(3.67)
Such a system is called forced as the vector of input variables u(t) appears on
the right hand side of the equation. However, stability can be studied on free
(zero-input) systems given by the equation
dx(t)
dt
= f(x(t),t), x(t
0
)=x
0
(3.68)
u(t) does not appear in the previous equation, which is equivalent to processes
with constant inputs. If time t appears explicitly as an argument in process
dynamics equations we speak about nonautonomous system, otherwise about
autonomous system.
In our discussion about stability of (3.68) we will consider stability of mo-
tion of x
s
(t) that corresponds to constant values of input variables. Let us for
this purpose investigate any solution (motion) of the forced system x(t) that
is at t = 0 in the neighbourhood of x
s
(t). The problem of stability is closely
connected to the question if for t ≥ 0 remains x(t) in the neighbourhood of
x
s
(t). Let us define deviation
˜x(t)=x(t) − x
s
(t) (3.69)
then,
d˜x(t)
dt
+
dx
s
(t)
dt
= f(˜x(t)+x
s
(t), u(t),t)
d˜x(t)
dt
= f(˜x(t)+x
s
(t), u(t),t) −f (x
s
(t),t)
d˜x(t)
dt
=
˜
f(˜x(t), u(t),t) (3.70)
The solution x
s
(t) in (3.70) corresponds for all t>0 to relation ˜x(t)=0
and
˙
˜x(t)=0. Therefore the state ˜x(t)=0 is called equilibrium state of
the system described by (3.70). This equation can always be constructed and
stability of equilibrium point can be interpreted as stability in the beginning
of the state-space.
Stability theorems given below are valid for nonautonomous systems. How-
ever, such systems are very rare in common processes. In connection to the

3.2 State-Space Process Models 73
above ideas about equilibrium point we will restrict our discussion to systems
given by
dx(t)
dt
= f(x(t)), x(t
0
)=x
0
(3.71)
The equilibrium state x
e
= 0 of this system obeys the relation
f(0)=0 (3.72)
as dx/dt = 0
We assume that the solution of the equation (3.71) exists and is unique.
Stability can be intuitively defined as follows: If x
e
= 0 is the equilibrium
point of the system (3.71), then we may say that x
e
= 0 is the stable equilib-
rium point if the solution of (3.71) x(t)=x[x(t
0
),t] that begins in some state
x(t
0
) “close” to the equilibrium point x
e
= 0 remains in the neighbourhood
of x
e
= 0 or the solution approaches this state.
The equilibrium state x
e
= 0 is unstable if the solution x(t)=x[x(t
0
),t]
that begins in some state x(t
0
) diverges from the neighbourhood of x
e
= 0.
Next, we state the definitions of stability from Lyapunov asymptotic sta-
bility and asymptotic stability in large.
Lyapunov stability: The system (3.71) is stable in the equilibrium state
x
e
= 0 if for any given ε>0, there exists δ(ε) > 0 such that for all x(t
0
) such
that x(t
0
)≤δ implies x[x(t
0
),t]≤ε for all t ≥ 0.
Asymptotic (internal) stability: The system (3.71) is asymptotically stable
in the equilibrium state x
e
= 0 if it is Lyapunov stable and if all x(t)=
x[x(t
0
),t] that begin sufficiently close to the equilibrium state x
e
= 0 satisfy
the condition lim
t→∞
x(t) =0.
Asymptotic stability in large: The system (3.71) is asymptotically stable
in large in the equilibrium state x
e
= 0 if it is asymptotic stable for all initial
states x(t
0
).
In the above definitions, the notation x has been used for the Euclidean
norm of a vector x(t) that is defined as the distance of the point given by the
coordinates of x from equilibrium point x
e
= 0 and given as x =(x
T
x)
1/2
.
Note 3.1. Norm of a vector is some function transforming any vector x ∈ R
n
to some real number x with the following properties:
1. x≥0,
2. x =0iffx = 0,
3. kx = |k|x for any k,
4. x + y≤x + y.
Some examples of norms are x =(x
T
x)
1/2
, x =
*
n
i=1
|x
i
|, x =
max |x
i
|. It can be proven that all these norms satisfy properties 1-4.
Example 3.6: Physical interpretation – U-tube
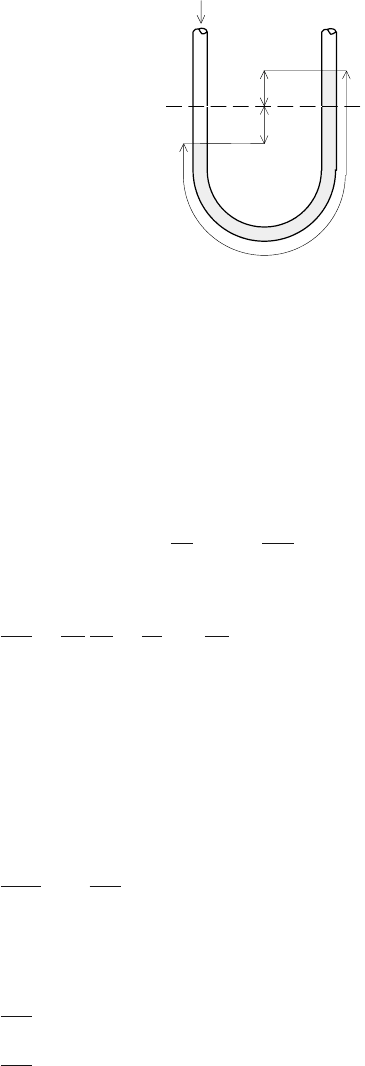
74 3 Analysis of Process Models
h
h
L
p
v
Fig. 3.5. AU-tube
Consider a U-tube as an example of the second order system. Mathemat-
ical model of this system can be derived from Fig. 3.5 considering the
equilibrium of forces.
We assume that if specific pressure changes, the force with which the liquid
flow is inhibited, is proportional to the speed of the liquid. Furthermore, we
assume that the second Newton law is applicable. The following equation
holds for the equilibrium of forces
Fp
v
=2Fgρh+ kF
dh
dt
+ FLρ
d
2
h
dt
2
or
d
2
h
dt
2
+
k
Lρ
dh
dt
+
2g
L
h =
1
Lρ
p
v
where
F - inner cross-sectional area of tube,
k - coefficient,
p
v
- specific pressure,
g - acceleration of gravity,
ρ - density of liquid.
If the input is zero then the mathematical model is of the form
d
2
x
1
dt
2
+ a
1
dx
1
dt
+ a
0
x
1
=0
where x
1
= h − h
s
,a
0
=2g/L,a
1
= k/Lρ. The speed of liquid flow will
be denoted by x
2
=dx
1
/dt.Ifx
1
,x
2
are elements of state vector x then
the dynamics of the U-tube is given as
dx
1
dt
= x
2
dx
2
dt
= −a
0
x
1
− a
1
x
2
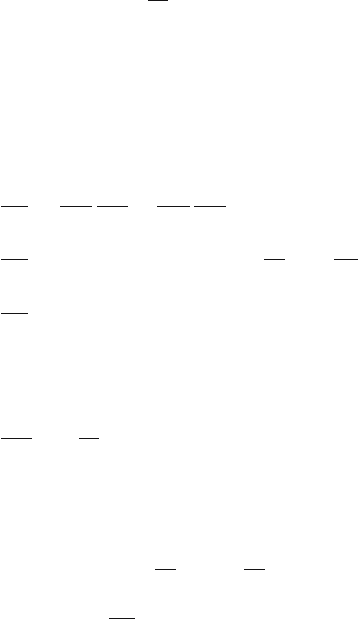
3.2 State-Space Process Models 75
If we consider a
0
=1,a
1
=1, x(0) = (1, 0)
T
then the solution of the
differential equations is shown in Fig. 3.6. At any time instant the total
system energy is given as a sum of kinetic and potential energies of liquid
V (x
1
,x
2
)=FLρ
x
2
2
2
+
x
1
0
2Fgρxdx
Energy V satisfies the following conditions: V (x) > 0, x = 0 and
V (0)=0.
These conditions show that the sum of kinetic and potential energies is
positive with the exception when liquid is in the equilibrium state x
e
= 0
when dx
1
/dt =dx
2
/dt =0.
The change of V in time is given as
dV
dt
=
∂V
∂x
1
dx
1
dt
+
∂V
∂x
2
dx
2
dt
dV
dt
=2Fgρx
1
x
2
+ FLρx
2
−
2g
L
x
1
−
k
Lρ
x
2
dV
dt
= −Fkx
2
2
As k>0, time derivative of V is always negative except if x
2
= 0 when
dV/dt = 0 and hence V cannot increase. If x
2
= 0 the dynamics of the
tube shows that
dx
2
dt
= −
2g
L
x
1
is nonzero (except x
e
= 0). The system cannot remain in a nonequilibrium
state for which x
2
= 0 and always reaches the equilibrium state which is
stable. The sum of the energies V is given as
V (x
1
,x
2
)=2Fgρ
x
2
1
2
+ FLρ
x
2
2
2
V (x
1
,x
2
)=
Fρ
2
(2gx
2
1
+ Lx
2
2
)
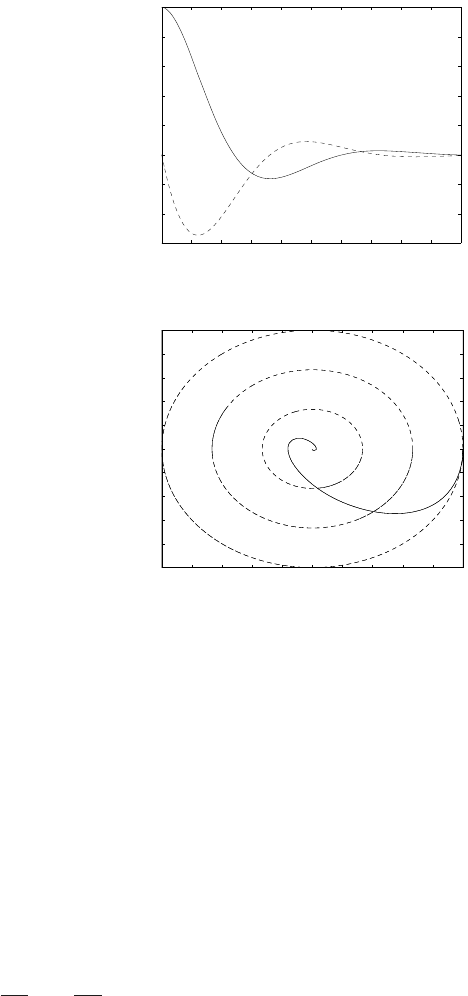
Fig. 3.7 shows the state plane with curves of constant energy levels V
1
<
V
2
<V
3
and state trajectory corresponding to Fig. 3.6 where x
1
,x
2
are
plotted as function of parameter t.
Conclusions about system behaviour and about state trajectory in the
state plane can be generalised by general state-space. It is clear that some
results about system properties can also be derived without analytical solution
of state-space equations.
Stability theory of Lyapunov assumes the existence of the Lyapunov func-
tion V (x). The continuous function V (x) with continuous derivatives is called
positive definite in some neighbourhood Δ of state origin if
V (0) = 0 (3.73)
and
76 3 Analysis of Process Models
0 1 2 3 4 5 6 7 8 9 10
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
t
x1,x2
Fig. 3.6. Time response of the U-tube for initial conditions (1, 0)
T
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
x1
x2
V1
V2
V3
Fig. 3.7. Constant energy curves and state trajectory of the U-tube in the state
plane
V (x) > 0 (3.74)
for all x = 0 within Δ. If (3.74) is replaced by
V (x) ≥ 0 (3.75)
for all x ∈ Δ then V (x)ispositive semidefinite. Definitions of negative definite
and negative semidefinite functions follow analogously.
Various definitions of stability for the system dx(t)/dt = f (x), f(0)=0
lead to the following theorems:
Stability in Lyapunov sense: If a positive definite function V (x)canbe
chosen such that
dV
dt
=
∂V
∂x
T
f(x) ≤ 0 (3.76)
then the system is stable in origin in the Lyapunov sense.
The function V (x) satisfying this theorem is called the Lyapunov function.
