Мишкин Фредерик С. Экономическая теория денег, банковского дела и финансовых рынков

Подождите немного. Документ загружается.

96 ЧАСТЬ I. Введение

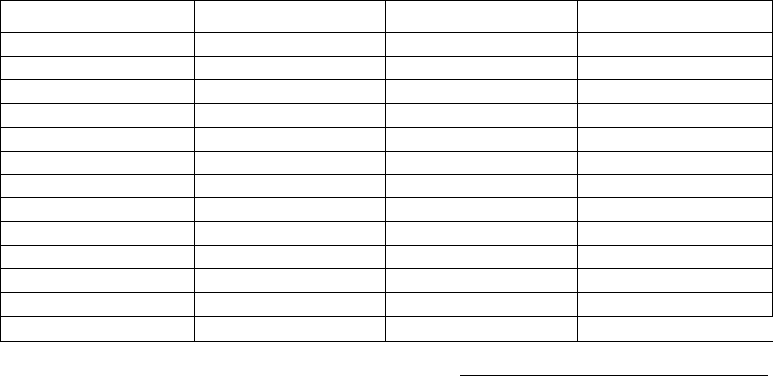
Таблица 3.2. Прирост М2: оперативные и уточненные данные

по месяцам 2002 года (в процентах, в годовом измерении)

Период

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

Среднегодовой прирост

Оперативные данные

2,2

6,8

-1,4

-4,0

14,8

7,6

13,6

9,9

5,1

10,9

10,2

2,8

6,5

Уточненные данные

5,4

8,7

0,2

-2,6

15,4

7,1

11,0

8,6

5,7

8,3

8,0

2,8

6,5

Отклонение

3,2

1,9

1,6

1,4

0,6

-0,5

-2,6

-1,3

0,6

-2,6

-2,2

0,0

0,0 |

Источник. Federal Reserve Statistical Release H.6; www. federalreserve.gov/releases/h6

Резюме

Для экономистов слово деньги имеет иное значение, чем доход или богатство.

Экономисты определяют деньги (денежную массу) как общепринятое сред-

ство платежа, принимаемое без ограничений в обмен на товары и услуги, а так-

же при погашении долговых обязательств.

2. Три главные функции денег, средство обмена, единица учета (мера стоимости),

средство сбережения. Деньги как средство обмена позволяют устранить про-

блему двойного совпадения желаний, характерную для бартерной экономики,

уменьшить операционные издержки, углубить специализацию и разделение

труда. Использование денег как единицы учета уменьшает количество цен, не-

обходимых экономике, что также сокращает операционные издержки. Деньги

одновременно функционируют как средство сбережения, но выполняют эту

роль не очень успешно, так как теряют стоимость вследствие инфляции.

3. Система платежей развивается во времени. Начиная с давних времен и до позд-

него средневековья во всех обществах, кроме самых примитивных, система

платежей базировалась главным образом на драгоценных металлах. Введение

бумажных денег позволило уменьшить транспортные издержки. Внедрение

чеков привело к дальнейшему снижению операционных издержек. Сейчас

мы находимся на этапе расширения масштабов использования электронной

системы платежей, в которой для проведения операций обмена используется

компьютер, т.е. не требуются бумажные деньги. Несмотря на потенциальную

эффективность такой системы, полный отказ от бумажных денег и развитие

новых форм электронных денег связаны с преодолением ряда препятствий.

4. Федеральная резервная система определила три показателя для измерения

количества денег — денежные агрегаты Ml, M2 и МЗ. Эти показатели не вза-

ГЛАВА 3. Что такое деньги

имозаменяемы, так как изменяются разными темпами и не всегда в одном на-

правлении. Однозначное точное измерение денежной массы необходимо для

обоснованного принятия важных решений при реализации экономической

и монетарной политики.

Другая проблема измерения денег — недостаточная надежность данных моне-

тарной статистики. Существенные отклонения уточненных значений монетар-

ных агрегатов от ранее опубликованных оперативных данных не позволяют

доверять данным о краткосрочных изменениях денежной массы, например

ежемесячным данным о приросте М2. Однако оперативные данные вполне

приемлемы для анализа более длительных периодов, например года.

Ключевые термины

М2

МЗ

богатство

гиперинфляция

денежные агрегаты

доход

единица учета (мера стоимости)

ликвидность

наличность

система платежей

смарт-карта

средство обмена

средство сбережения

товарные деньги

фидуциарные бумажные деньги

электронные деньги

электронная наличность

Вопросы и задания

На вопросы, отмеченные звездочкой, ответы приведены в конце книги (в прило-

жении "Ответы на некоторые вопросы и задания").

1. Какое из следующих трех выражений опирается на экономическое определе-

ние денег:

а) "Сколько денег вы заработали на прошлой неделе?"

б) "Когда я иду в магазин, то всегда проверяю, достаточно ли у меня денег."

в) "Любовь к деньгам — корень зла."

2. *В экономике три товара производятся тремя производителями

Товар Производитель

Яблоки Владелец яблоневого сада

Бананы Владелец банановой плантации

Шоколад Владелец шоколадного цеха

Если владелец яблоневого сада любит только бананы, владелец банановой

плантации — только шоколад, а владелец шоколадного цеха — только яблоки,

возможна ли торговля между этими производителями в бартерной экономике?

Как производители выиграют от введения денег?

3. Почему первобытным людям не нужны были деньги?

ЧАСТЬ I. Введение

4. * Почему американцы в XIX веке часто отдавали предпочтение чекам, а не зо-

лоту, даже зная, что банк может вернуть чек ввиду отсутствия денег на счету?

5. Почему в Древней Греции золото было более вероятным кандидатом на роль

денег, чем вино?

6. *В какие годы деньги в США лучше выполняли роль средства сбережения:

в 1950-е или 1970-е? Почему? В какой период вы бы предпочли сберегать

деньги?

7. Готовы ли вы отказаться от вашей чековой книжки и использовать электрон-

ную систему платежей? Почему "да" или почему "нет"?

8. Расположите указанные активы по степени уменьшения их ликвидности:

а) текущие счета;

б) дома;

в) наличность;

г) стиральные машины;

д) сберегательные вклады;

е)

обыкновенные акции.

9. * Почему некоторые экономисты описывали деньги во время гиперинфляции

как "горячую картошку", которую быстро передают из рук в руки?

10. В Бразилии, которая до 1994 года переживала высокую инфляцию, многие

сделки проводились в долларах, а не во внутренней валюте (реалах). Почему?

П.*Предположим, некий исследователь пришел к выводу, что показатель общей

суммы долга в экономике США в течение последних 20 лет лучше предсказы-

вал инфляцию и циклы деловой активности, чем значения Ml, M2 или МЗ.

Означает ли это открытие, что нам следует определить деньги как общую сум-

му долга в экономике?

12.Посмотрите на показатели Ml, M2 и МЗ в бюллетене Федерального резерва

за последний полный год. Отличаются ли между собой темпы их роста? Какое

значение имеют темпы роста этих агрегатов для проведения монетарной по-

литики?

13.*Какой из денежных агрегатов Федеральной резервной системы (Ml, M2 или

МЗ) состоит из самых ликвидных активов? Какой агрегат имеет самый широ-

кий охват?

14. Для каждого из следующих активов укажите, в какой из денежных агрегатов

(Ml, M2 или МЗ) они входят:

а) наличность;

б) паи взаимных фондов денежного рынка;

в)евродоллары;

г) мелкие срочные депозиты;

д) крупные соглашения о покупке ценных бумаг с выкупом;

е) чековые депозиты.

ГЛАВА 3. Что такое деньги

15.*Почему пересмотр и уточнение денежных агрегатов представляют меньше

проблем для определения долгосрочной динамики предложения денег, чем для

анализа краткосрочной динамики?

Web-упражнения

1. Обратитесь по адресу www. federalreserve.gov/releases/h6/Current/

и ответьте на следующие вопросы:

а) Каким был темп роста денежных агрегатов Ml, M2, МЗ за последние 12 ме-

сяцев?

б) Какой показатель говорит о том, на какой стадии делового цикла — оживления

или спада — находится экономика?

2. Обратившись по адресу www. federalreserve. gov/paymentsys . htm, вы-

берите один из аналитических отчетов Федерального резерва. Напишите резю-

ме этого материала (1 абзац).

ЧАСТЬ II

Финансовые

рынки

Глава 4

Процентные ставки

Предисловие

www.bloomberg.com/markets/

В разделе Rates&Bonds ("Процентные ставки и облигации") содержится информация

о важнейших процентных ставках, правительственных и муниципальных облигациях.

Процентные ставки — одна из наиболее часто исследуемых экономических

переменных. Средства массовой информации практически ежедневно

публикуют данные о процентных ставках, так как эти показатели

непосредственно отражаются на нашей повседневной жизни и имеют большое

значение для состояния экономики в целом. Процентные ставки влияют на

ваше личное решение о покупке дома, приобретении акций или пополнении

банковского счета. Они также влияют на экономические решения предприятий

и домохозяйств по поводу того, инвестировать ли им фонды в новое

оборудование или сберегать деньги в банке.

Прежде чем продолжить изучение денег, банковского дела и финансовых

рынков, мы должны точно определить значение термина процентные ставки.

Мы считаем, что в данной главе для определения процентных ставок лучше

всего использовать понятие доходность к погашению; говоря о процентных

ставках, экономисты имеют в виду именно этот показатель. В данной главе

рассматриваются методики измерения доходности к погашению, а также

альтернативные (но менее точные) показатели процентных ставок. Мы также

увидим, что процентная ставка по облигациям не обязательно показывает,

насколько инвестирование в них будет выгодным, так как отдача от облигации

(норма доходности) не обязательно равна процентной ставке. Наконец, мы

научимся различать реальные процентные ставки (скорректированные с учетом

инфляции) и номинальные процентные ставки (без учета инфляции).

Хотя изучение определений — не самое увлекательное занятие, основные

положения настоящей главы требуют внимательного прочтения и понимания.

Ключевые понятия, введенные в данной главе, постоянно используются

в последующих главах книги. Помимо этого, четкое усвоение этих понятий

поможет вам лучше понять, какое значение имеют процентные ставки для

каждого из нас и для экономики в целом.

Измерение процентных ставок

Каждый долговой инструмент предполагает свои сроки определенных поступле-

ний. Прежде чем перейти к рассмотрению подходов к измерению процентных ставок,

104 ЧАСТЫ!. Финансовые рынки

убедимся в том, что стоимость различных долговых инструментов можно сопоста-

вить, используя понятие текущей стоимости.

Текущая стоимость

Понятие текущей стоимости (текущей дисконтированной стоимости) исходит из

обычного понимания того, что доллар, который вы будете иметь через год, стоит мень-

ше доллара, полученного вами сегодня. Действительно, вы можете положить доллар на

сберегательный счет, приносящий проценты, и через год получить больше доллара.

Перейдем к более формальным рассуждениям. Рассмотрим простейший вид

долгового обязательства — простую ссуду. В этом случае кредитор предоставляет

заемщику определенные средства (так называемую основную сумму долга), подле-

жащие возврату на дату погашения вместе с дополнительной суммой (процентным

платежом). Например, если вы предоставили своему другу простую ссуду в 100 долл.

сроком на один год, он должен вернуть через год 100 долл. вместе с процентным пла-

тежом в сумме, скажем, 10 долл. Отношение дополнительной суммы (процентного

платежа) к основной сумме долга (так называемая простая процентная ставка) ~

естественный и удобный способ измерения процентной ставки по простой ссуде.

В нашем случае процентная ставка равна 10%:

10долл.

1 =

= 0,10 = 10%.

100 долл.

Предоставив простую ссуду в 100 долл., в конце года вы получите 110 долл.:

100 долл. х(1 +0,10) =110 долл.

Если в конце первого года отдать в ссуду полученные 110 долл. сроком на год, то

в конце второго года получим:

ИОдолл. х (1 +0,10) = 121 долл.,

или

100долл. х (1+0,10) х (1 + 0,10) = 100долл. х (1+0,10)

= 121 долл.

Предоставляя простую ссуду еще на год, в конце третьего года получим:

121 долл. х (1 + 0,10) = 100 долл. х (1 + 0,10)

= 133 долл.

В общем случае, через и лет наши 100 долл. превращаются в такую сумму:

100долл. х (l + i)\

Сегодня Год Год Год Год

W h

$100 $110 $121 $133 $100х(1+0,10)

Приведенные формулы показывают, что 100 долл. сегодня стоят столько, сколько

121 долл. через два года, или 133 долл. через три года, или 100 х (1+0,10)" долларов

через п лет. Мы можем также производить расчеты в обратном порядке — от будущей

стоимости к сегодняшней. Например, 133 долл. через три года стоят 100 долл. сегодня:

133 долл.

100 долл. =

(1 + 0Д0)

ГЛАВА 4. Процентные ставки 105

Вычисление сегодняшней стоимости денег, которые будут получены в будущем,

называется дисконтированием будущей стоимости. Мы можем записать общую фор-

мулу вычисления сегодняшней (текущей) дисконтированной стоимости PV, если бу-

дущая стоимость составит FV через п лет при процентной ставке г:

(1 + 0 (4.1)

Уравнение (4.1) математически выражает интуитивное представление о том, что

один доллар, обещанный вам через 10 лет, стоит меньше, чем один доллар сегодня,

поскольку имея один доллар сегодня, вы можете его инвестировать и получить боль-

ше одного доллара через 10 лет.

Понятие текущей стоимости исключительно полезно, так как позволяет вычис-

лить сегодняшнюю стоимость (цену) инструментов кредитного рынка при данной

простой процентной ставке простым суммированием текущих дисконтированных

стоимостей всех будущих доходов. Именно это позволит нам сопоставить стоимость

инструментов с различными сроками платежей по ним.

Проиллюстрируем понятие текущей стоимости на примере. Предположим, вы

только что выиграли Джек-пот в лотерею штата Нью-Йорк в сумме 20 млн. долл. По

условиям лотереи, вам предстоит получать по миллиону долларов в течение 20 лет.

Вы пребываете в невероятном восторге, но действительно ли ваш выигрыш составил

20 млн. долл.? Нет, в смысле текущей стоимости. Сумма, которую вы получите, будет

стоить значительно меньше сегодняшних 20 млн. долл. Предположим, процентная

ставка составляет те же 10%, что и в предыдущем примере. Если первый платеж в

1 млн. долл. действительно равен 1 млн. сегодняшних долларов, то уже второй пла-

теж (в следующем году) будет стоить только 909 090 текущих долларов — значитель-

но меньше миллиона. Третий — 826 446 сегодняшних долларов, и т.д. Сумма всех

двадцати платежей составит 9,4 млн. долл. Вы, конечно, по-прежнему в восторге, но

вычисление текущей стоимости подсказывает вам, что вы — жертва недобросовест-

ной рекламы. Вы выиграли не 20 млн. долл., а меньше половины этой суммы.

Четыре инструмента кредитного рынка

Рассмотрим четыре основных инструмента кредитного рынка с точки зрения сро-

ков платежей по долговым обязательствам.

1. Простая ссуда, рассмотренная выше: кредитор предоставляет заемщику некото-

рую сумму, подлежащую возврату на дату погашения вместе с дополнительной сум-

мой (процентным платежом). Многие инструменты кредитного рынка относятся к

этому виду: например, коммерческие ссуды предприятиям.

2. Ссуда

с фиксированными платежами (или полностью амортизированная ссу-

да): кредитор предоставляет заемщику некоторую сумму, подлежащую возврату в

виде регулярных (например, ежемесячных) выплат равными частями вместе с про-

центами за определенное количество лет. Например, если вы одолжили 1000 долл.,

то, по условиям ссуды с фиксированными платежами, вам придется выплачивать,

скажем, 126 долл. в течение 25 лет. Продажа товаров в кредит (в рассрочку) и заклад-

ные — примеры ссуд с фиксированными платежами.

106 ЧАСТЬ II. Финансовые рынки

3. Купонная облигация предоставляет своему собственнику постоянный процент-

ный доход (купонный платеж) ежегодно до срока погашения, когда выплачивается

установленная конечная сумма — номинальная стоимость (номинал, или паритет).

В былые времена владелец облигации получал купонный платеж, отрезая купон от

облигации и посылая его ее эмитенту, который затем высылал владельцу определен-

ную сумму платежа. Сегодня нет необходимости высылать купон для получения до-

хода. Имея купонную облигацию номиналом, например, 1000 долл., вы можете по-

лучать купонные платежи в размере 100 долл. в течение 10 лет, а при погашении -

номинальную стоимость в сумме 1000 долл. (Как правило, номинальная стоимость

облигации кратна 1000 долл.)

Отличительные характеристики купонной облигации:

1) эмитент (корпорация или государственный орган, выпустивший облигацию);

2) срок погашения облигации;

3) купонная ставка — процентное отношение ежегодного купонного платежа

к номинальной стоимости облигации.

В нашем примере купонная облигация приносит ежегодный купонный платеж

100 долл. при номинальной стоимости 1000 долл. Купонная ставка равна 100 долл./

/1000 долл. = 0,10, или 10%. Примеры купонных облигаций — казначейские и корпо-

ративные облигации.

4. Дисконтная

облигация (облигация с нулевым купоном) покупается по цене

ниже номинала (со скидкой), а ее номинальная стоимость выплачивается в момент

погашения облигации. В отличие от купонной облигации, дисконтная облигация

не приносит доход в виде процента; по ней выплачивается только ее номинальная

стоимость. Например, дисконтная облигация номиналом 1000 долл. продается за

900 долл., а через год владелец облигации получит ее номинальную стоимость -

1000 долл. Казначейские векселя, сберегательные облигации и долгосрочные облига-

ции с нулевым купоном — примеры дисконтных облигаций.

Различные инструменты кредитного рынка предусматривают платежи в разные

сроки: простые ссуды и дисконтные облигации — только в момент погашения, а ссуды

с фиксированными платежами и купонные облигации — периодически до момента

погашения. Как же определить наиболее доходный вид долгового инструмента? Как

сопоставить различные инструменты, предусматривающие платежи в разное время?

Именно рассмотренное выше понятие текущей стоимости лежит в основе методики

измерения процентных ставок по различным инструментам кредитного рынка.

Доходность к погашению

Основной способ измерения процентных ставок — вычисление доходности к по-

гашению на основе равенства текущей дисконтированной стоимости поступлений по

долговому инструменту и его сегодняшней стоимости

. Экономисты считают, что до-

ходность к погашению — самый точный измеритель процентных ставок.

Рассмотрим методику расчета доходности к погашению для четырех основных

инструментов кредитного рынка.

В других случаях употребляется термин внутренняя норма доходности.

ГЛАВА 4. Процентные ставки 107

Простая ссуда

Доходность к погашению для простой ссуды легко вычисляется на основе концеп-

ции текущей стоимости. Для ссуды сроком на один год из рассмотренного выше при-

мера сегодняшняя стоимость основной суммы долга равна 100 долл., а через год будет

получен платеж в сумме ПО долл. (возврат 100 долл. основного долга, плюс 10 долл.

процентного платежа). Мы можем вычислить доходность к погашению г исходя из

того, что текущая дисконтированная стоимость полученных платежей должна быть

равна сегодняшней стоимости основной суммы долга. Приравнивая сегодняшнюю

стоимость основного долга (100 долл.) и текущую стоимость платежа 110 долл. через

год (см. уравнение 4.1), получим:

НО долл.

100долл. =

1 + i

Решим уравнение относительно i:

НО долл. - 100 долл. 10 долл.

= 0,10 = 10%.

100 долл. 100 долл.

Как видим, доходность к погашению равна отношению 10 долл. процентного платежа

к 100 долл. основного долга, т.е. простой процентной ставке по предоставленной ссуде.

Следовательно, для простой ссуды простая процентная ставка равна доходности к по-

гашению. Поэтому для обеих величин используется одно и то же обозначение i.

Учись, студент!

Главное в расчете доходности к погашению — равенство сегодняшней стоимости

долгового инструмента и текущей дисконтированной стоимости всех будущих плате-

жей по нему. Чтобы усвоить этот принцип, примените его к другим инструментам кре-

дитного рынка, придумав свои примеры. Убедитесь, что вы можете вывести уравнение

для вычисления доходности к погашению в каждом случае.

Ссуда с фиксированными платежами

Напомним, что этот вид ссуды предполагает одинаковые периодические платежи

до даты погашения долга. По закладной с фиксированным процентом заемщик, на-

пример, платит банку одинаковую сумму ежемесячно до даты погашения. Чтобы вы-

числить доходность к погашению для ссуды с фиксированными платежами, исполь-

зуем тот же подход, что и для простой ссуды: приравняем сегодняшнюю стоимость

долга к сумме текущих дисконтированных стоимостей всех платежей (поскольку в

этом случае платежей несколько).

В рассмотренном выше примере основная сумма долга составляет 1000 долл., а еже-

годный платеж — 126 долл. на протяжении 25 лет. Текущая стоимость (PV) рассчиты-

вается следующим образом: PV платежа в конце первого года равна 126/( 1+i) долл.;

PV платежа в конце второго года— 126/(l+i)

долл., и т.д. В конце 25-го года

состоится последний платеж с PV 126/( 1+i)

долл. Приравнивая сегодняшнюю

стоимость долга (1000 долл.) к сумме текущих стоимостей всех ежегодных пла-

тежей, получаем:

.... 126долл. 126 долл. 126 долл. 126 долл.

1000 долл. = + г— + 5— + ••• + тг

•

1 + i (1 + i)

(1 + i)