Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

ОТК i можливих виплатах фiрмi. Виграшем другого гравця є очiкувана
сума виплат, одержаних вiд заводу при перевiрцi партiї автомобiлiв з
врахуванням витрат на цю перевiрку. Випишемо матрицi гри
A =
100 100
90 130
,B=
−12 0
40
.
Наприклад, якщо завод не проводить ОТК, а фiрма перевiряє партiю, то
середнi премiальнi рiвнi
100(0.8(4/5) + 1.3(1/5)) = 90 од., а очiкуваний
прибуток фiрми складе
100(0.08(4/5)−0.12(1/5)) = 4 од. Неважко бачити,
що в данiй грi не iснує ситуацiї рiвноваги в чистих стратегiях. Умови
(2.9.7) i (2.9.9) виконанi i ситуацiю рiвноваги знаходимо за формулами
(2.9.8) i (2.9.10). Рiвноважнi стратегiї
X
0
i Y
0
можуть бути реалiзованi
у виглядi “фiзичних сумiшей”: перший гравець “повинен” 25 автомобiлiв
кожної партiї випускати з ОТК, другий гравець повинен перевiряти по
75 автомобiлiв кожної партiї.
Приклад 2.9.10. Нехай
A =
245
421
,B=
320
023
.
Тут l
1
(x)=3x,l
2
(x)=2,l
3
(x)=3(1−x). Перша точка верхньої огинаючої
(перетин прямих
l
2
(x),l
3
(x))маєабсцисуx
0
=1/3.Розглянемосистему
рiвнянь з (2.9.5)
4y =5(1− y)=v
1
, 2y +(1− y)=v
1
.
Знаходимо y
0
=2> 1,щонедопустимо.Переходимододругоїточки
верхньої огинаючої, що лежить на перетинi прямих
l
1
(x),l
2
(x).Вонамає
абсцису
x
0
=2/3.Система
2y =4(1− y)=v
1
, 4y +2(1− y)=v
1
.
має розв’язок y
0
=1/2,v
1
=3.Тому
(X
0
,Y
0
) = ((2/3,1/3),(1/2,1/2,0)) −
шукана ситуацiя рiвноваги в змiшаних стратегiях.
Вiдзначимо, що даний алгоритм не завжди приводить до знаходження
всiх ситуацiй рiвноваги.
Приклад 2.9.11. Нехай
A =
01
10
,B=
22
−13
.
Тут перетин прямих l
1
(x),l
2
(x) дає стратегiю (1,0) з нульовою компонен-
тою (вироджений випадок). Розв’язуючи систему рiвнянь з (2.9.5), знахо-
димо
y
0
=(1/2,1/2). Одержана ситуацiя рiвноваги не єдина. Дiйсно, за-
пишемо умову (2.9.5) для стратегiї
(y
0
,1−y
0
) другого гравця з урахуван-
ням властивостi доповнюючої нежорсткостi
1−y
0
= v
1
,y
0
≤ v
1
,0 ≤ y
0
≤ 1.
151

Звiдси y
0
≤ 1/2. Таким чином в даному прикладi одержали цiлий вiдрi-
зок ситуацiй рiвноваги
{((1,0),(y
0
,1 − y
0
)) : 0 ≤ y
0
≤ 1/2}.
Для гри з матрицями розмiрiв
3 × 3 пошук змiшаних рiвноваг Неша
вже вимагає досить великої кiлькостi перебору пiдматриць початкових
матриць
A i B. Однак в деяких випадках, що обговорюються в наступних
двох параграфах, цей перебiр можна значно скоротити.
Означення 2.9.5. Ситуацiя рiвноваги називається цiлком змiшаною,як-
що всi чистi стратегiї використовуються з додатними ймовiрностями.
Цiлком змiшана рiвновага може iснувати лише тодi, коли
m = n.Це
iнтуїтивно зрозумiло: для знаходження змiшаної стратегiї другого грав-
ця, в якiй всi компоненти вiдмiннi вiд нуля, потрiбно розв’язати систему
рiвнянь (2.9.5), що мiстить
m +1 рiвняння та n +1 невiдомих (число
елементiв множини
Y плюс ще одне невiдоме v
1
). Отже, для iснування
розв’язку повинна виконуватися умова
n ≥ m. Аналогiчно, змiшана стра-
тегiя першого гравця задовольняє системi рiвнянь з (2.9.6), що мiстить
n +1 рiвняння з m +1 невiдомими, i для iснування розв’язку повинна
виконуватися умова
m ≥ n. В результатi одержуємо, що для iснуван-
ня розв’язку обох систем повинно бути
m = n,якщообидвiсистеми
невиродженi.
Випишемо для цiлком змiшаної рiвноваги
(X
0
,Y
0
) системи рiвнянь з
(2.9.5) (2.9.6) в матричному виглядi
AY
0
= v
1
e, Y
0
,e =1,X
0
B = v
2
e, X
0
,e =1,
де e =(1,...,1) ∈ R
n
.НехайматрицiA i B – невиродженi. Тодi
Y
0
=
A
−1
e
A
−1
e,e
,v
1
=
1
A
−1
e,e
,X
0
=
eB
−1
eB
−1
,e
,v
2
=
1
eB
−1
,e
.
Для пошуку ситуацiй рiвноваги в бiматричних iграх можна викори-
стовувати домiнування рядкiв матрицi
A i стовпцiв матрицi B.
Означення 2.9.6. Говоритимемо, що в бiматричнiй грi
Γ стратегiя пер-
шого гравця
i
1
строго домiнує стратегiю i
2
(позначається i
1
i
2
)на
множинi
Q ⊂{1,...,n},якщоa
i
1
j
>a
i
2
j
∀j ∈ Q. Говоритимемо про слаб-
ке домiнування (
i
1
i
2
), якщо a
i
1
j
≥ a
i
2
j
∀j ∈ Q.
При строгому домiнуваннi стратегiя
i
1
приносить першому гравцю
бiльший виграш, нiж стратегiя
i
2
, як би не грав другий гравець, викори-
стовуючи стратегiї з множинi
Q. Аналогiчно вводяться поняття строгого
i слабкого домiнування для стратегiй другого гравця.
Означення 2.9.7. Говоритимемо, що в бiматричнiй грi
Γ стратегiя дру-
гого гравця
j
1
строго домiнує стратегiю j
2
(j
1
j
2
) на множинi P ⊂
{1,...,m}
,якщоb
ij
1
>b
ij
2
∀i ∈ P . Говоритимемо про слабке домiнуван-
ня (
j
1
j
2
), якщо b
ij
1
>b
ij
2
∀i ∈ P .
152
Опишемо процедуру послiдовного виключення стратегiй, якi стро-
го домiнуються. Ця процедура полягає в побудовi двох послiдовностей
вкладених множин
P
k
⊂··· ⊂P
2
⊂ P
1
⊂{1,...,m} i Q
k
⊂··· ⊂Q
2
⊂
Q
1
⊂{1,...,n} .Прицьомудляl =1,2,...,k−1 виконанi наступнi умови:
∀i
2
∈ P
l
\ P
l+1
∃i
1
∈ P
l+1
: i
1
i
2
на Q
l
;
∀j
2
∈ Q
l
\ Q
l+1
∃j
1
∈ Q
l+1
: j
1
j
2
на P
l
;
Ми описали процедуру послiдовного виключення стратегiй формально.
Подивимося тепер, як ця процедура здiйснюється на практицi.
Крок 1. Вважаємо
P
1
= {1,...,m}, Q
1
= {1,...,n} i будуємо множини
P
2
, Q
2
. Для цього викидаємо з множини P
1
всi стратегiї, якi строго домi-
нуються на множинi
Q
1
, тобто ми шукаємо такi пари стратегiй i
1
,i
2
,що
рядок
i
1
поелементно бiльше рядка i
2
вматрицiA: a
i
1
j
>a
i
2
j
.Викреслю-
ємо всi такi рядки
i
2
в обох матрицях. Аналогiчно шукаємо стовпцi j
2
вматрицiB другого гравця, якi строго домiнуються iншими стовпцями
j
1
: b
ij
1
>b
ij
2
. Викреслюємо всi такi стовпцi j
2
з обох матриць. Припу-
стимо, що нам вдалося викреслити принаймнi один рядок або стовпець.
Тодi переходимо до кроку 2.
Крок 2. Пiсля викреслювання рядкiв i стовпцiв на першому кроцi ми
одержали матрицi, в яких множина рядкiв
P
2
,амножинастовпцiвQ
2
.
При цьому або
P
1
= P
2
,абоQ
1
= Q
2
, або обидвi множини не спiвпада-
ють з попереднiми. Може вийти так, що новi матрицi матимуть рядки i
стовпцi, якi строго домiнуються Викреслюємо їх i переходимо до насту-
пного кроку. Продовжуємо процедуру до тих пiр, поки не викреслимо
все, що можна. Нижче доведено, що при цьому зберiгаються всi змiшанi
рiвноваги Неша.
Означення 2.9.8. Говоритимемо, що множина
Z = P ×Q строго домiнує
множину
Z = P ×Q (Z Z), якщо вона одержана з множини Z послiдов-
ним виключенням стратегiй, якi строго домiнуються, тобто в описанiй
вище процедурi
P = P
k
, Q = Q
k
. Говоритимемо про слабке домiнування
(
Z Z), якщо множина Z одержана з множини Z послiдовним виклю-
ченням стратегiй, якi слабко домiнуються.
Розглянемо поняття домiнування в змiшаних стратегiях.
Означення 2.9.9. Говоритимемо, що змiшана стратегiя
X строго до-
мiнує чисту стратегiю
i на множинi Q ⊂{1,...,n} (X i), якщо
A(X,j) >a
ij
∀j ∈ Q. Говоритимемо про слабке домiнування на множинi
Q ⊂{1,...,n} (X i), якщо A(X,j) ≥ a
ij
∀j ∈ Q.
Аналогiчно визначається домiнування в змiшаних стратегiях другого
гравця.
Як шукати стратегiї, якi строго домiнуються?
153
Приклад 2.9.12. Розглянемо гру Γ зматрицями
A =
−402
4 −17
−530
,B=
444
−131
−4 −21
.
Знайдемо в кожному стовпцi першої матрицi максимальний елемент.
Якщо максимум єдиний i стоїть в деякому рядку, то вiн не може бу-
ти таким, що строго домiнується. Отже, таким, що строго домiнується
може бути лише перший рядок. У чистих стратегiях домiнування немає.
Дослiджуємо домiнування в змiшаних стратегiях. Вiзьмемо другий i тре-
тiй рядки з коефiцiєнтами
1/2. Видно, що ця комбiнацiя строго домiнує
перший рядок.
Визначимо поняття слабо i строго домiнуючих множин для змiшаних
стратегiй.
Означення 2.9.10. Говоритимемо, що множина
Z = P × Q строго до-
мiнує множину
Z = P × Q (Z Z), якщо вона одержана з множини
Z послiдовним виключенням стратегiй, якi строго домiнуються, тобто
в описанiй вище процедурi
P = P
k
, Q = Q
k
. Говоритимемо про слабке
домiнування (
Z Z), якщо множина Z одержана з множини Z послi-
довним виключенням стратегiй, якi слабко домiнуються.
Означення 2.9.11. Говоритимемо, що множина
Z = P × Q строго домi-
нує множину
Z = P × Q у змiшаних стратегiях (Z Z), якщо вона
одержана з множини
Z послiдовним виключенням стратегiй, якi строго
домiнуються за змiшаним домiнуванням стратегiй, тобто
Z = Z
k
⊂ Z
k−1
⊂···⊂Z
1
= Z, Z
l
= P
l
× Q
l
,l =1,...,k,
iвиконанiумови
∀i ∈ P
l
\ P
l+1
∃x ∈ X : x i на Q
l
i ∀s/∈ P
l+1
x
s
=0;
∀j ∈ Q
l
\ Q
l+1
∃y ∈ Y : y j на P
l
i ∀k/∈ Q
l+1
y
k
=0.
Говоритимемо, що множина Z = P × Q слабо домiнує множину Z =
P ×Q
у змiшаних стратегiях (Z Z), якщо вона одержана з множини Z
послiдовним виключенням стратегiй, якi слабо домiнуються за змiшаним
домiнуванням стратегiй, тобто
Z = Z
k
⊂ Z
k−1
⊂···⊂Z
1
= Z, Z
l
= P
l
× Q
l
,l =1,...,k,
iвиконанiумови
∀i ∈ P
l
\ P
l+1
∃x ∈ X : x i на Q
l
i ∀s/∈ P
l+1
x
s
=0;
∀j ∈ Q
l
\ Q
l+1
∃y ∈ Y : y j на P
l
i ∀k/∈ Q
l+1
y
k
=0.
Якi зв’язанi рiзнi вiдносини домiнування?
Повернемося до прикладу 2.9.12 i знайдемо домiнуючi множини. Пер-
ший рядок ми викреслили, оскiльки вона строго домiнується комбi-
нацiєю другого i третього рядкiв. Розглянемо другу матрицю. Можна
154
помiтити, що перший стовпець строго домiнується, наприклад, другим
стовпцем. Отже, перший стовпець можна викреслити. Отримуємо, що
{2,3}×{2,3}Z.
Тепер сформулюємо теорему про зв’язок мiж виключенням стратегiй,
якiдомiнуютьсяiпроблемоюпошукузмiшанихравновагНеша.
Теорема 2.9.5. 1) Нехай множина
Z = P × Q строго домiнує мно-
жину
Z = P × Q в змiшаних стратегiях. Тодi для будь-якої ситуацiї
рiвноваги
(X
0
,Y
0
) виконанi умови
i/∈ P ⇒ x
0
i
=0; j/∈ Q ⇒ y
0
j
=0.
2) Нехай множина Z = P ×Q слабо домiнує множину Z = P ×Q взмi-
шаних стратегiях i
(X
0
,Y
0
) – ситуацiя рiвноваги в грi зматрицями
A =(a
ij
)
i∈P,j∈Q
, B =(b
ij
)
i∈P,j∈Q
.
Визначимо змiшанi стратегiї
x
0
i
=
x
i
,i∈ P
0,i∈ P \
P ;
y
0
j
=
y
j
,j∈ Q
0,j∈ Q \
Q.
Тодi (X
0
,Y
0
) – ситуацiя рiвноваги в початковiй грi Γ.
Друге твердження теореми говорить про те, що якщо нова гра одер-
жана шляхом виключення стратегiй, що слабо домiнуються, то кожнiй
змiшанiй рiвновазi Неша
(X,Y ) в цiй новiй грi вiдповiдатиме змiша-
на рiвновага Неша
(X
0
,Y
0
) в початковiй, яка визначається за вказаним
правилом. Перше твердження теореми показує, що при викреслюваннi
рядкiв i стовпцiв при строгому домiнуванню ми не втрачаємо рiвноваг
Неша.
Отже, для пошуку всiх рiвноваг Неша можна викреслити всi рядки
i стовпцi, що строго домiнуються i шукати рiвновагу в новiй грi. До-
повнивши нулями знайдену рiвновагу, ми одержимо змiшану рiвновагу
в початковiй грi. Якщо необхiдно знайти принаймнi одну змiшану рiв-
новагу Неша, то можна викреслювати рядки i стовпцi, використовуючи
нестроге домiнування. Виключення рядкiв i стовпцiв дозволяє скоротити
перебiр пiдматриць для пошуку рiвноваг Неша. В прикладi 2.9.12 пiсля
виключення стратегiй, що строго домiнуються, одержимо гру
A =
−17
30
,
B =
31
−21
.
Уцiйгрiситуацiя(X,Y ) = ((3/5,2/5),(7/11,4/11)) є єдиною змiшаною
рiвновагою Неша. Отже, ситуацiя
(X,Y ) = ((0,3/5,2/5),(0,7/11,4/11)) є
змiшаною рiвновагою Неша в початковiй грi.
155

Приклад 2.9.13. Розглянемо гру Γ зматрицями
A =
2060
3204
0370
1131
,B=
7260
0104
0223
5343
.
Шукаємо максимальнi елементи в стовпцях першої матрицi. В чистих
стратегiях домiнування немає. Розглянемо домiнування в змiшаних стра-
тегiях. Видно, що четвертий рядок строго домiнується комбiнацiєю дру-
гого i третього рядкiв з вагами 1/2. Тому її можна викреслити.
Тепер знайдемо максимальнi елементи в рядках другої (зредукова-
ної) матрицi. Другий стовпець строго домiнується комбiнацiєю першого
i четвертого стовпцiв з вагами
1/3 − ε та 1/3 − ε при малих ε>0.
Ми можемо викреслити другий стовпець. Отже,
{1,2,3}×{1,3,4 Z.
В результатi виключення четвертого рядка i другого стовпця одержимо
наступнi зредукованi матрицi:
A =
260
304
070
,
B =
760
004
023
.
Повторюємо процедуру виключення стратегiй для зредукованих матриць.
Шукаємо максимальнi елементи в стовпцях першої матрицi. У чистих
стратегiях домiнування немає. Розглянемо домiнування в змiшаних стра-
тегiях. Другий i третiй рядок виключити неможливо, оскiльки в них мi-
стяться максимальнi по стовпцях елементи. Перший рядок не мiстить
жодного максимального по стовпцю елементу, проте її також неможливо
виключити, оскiльки вiн не домiнується жодною лiнiйною комбiнацi-
єю другого i третього рядка. Аналогiчно, неможливо виключити жоден
стовпець в другiй матрицi.
Отже, процедура виключення по домiнуванню змiшаними стратегiями
завершена i
{1,2,3}×{1,3,4} = Z.
2.9.1. Контрольнi запитання i задачi для самостiйної роботи
1. Що таке бiматрична гра?
2. Що таке ситуацiя рiвноваги. Якi бувають ситуацiї рiвноваги?
3. Опишiть алгоритм пошуку рiвноваги у змiшаних стратегiях.
4. Як пов’язана проблема пошуку рiвноваг Неша iз домiнуючими стра-
тегiями?
156
5. Якi недолiки має рiвновага Неша?
6. Визначiть поняття слабо i строго домiнуючих множин для змiша-
них стратегiй.
Задачi
1. Якщо F (x,y)=−G(x,y),тограΓ – антагонiстична. Доведiть, що
в антагонiстичнiй грi ситуацiї рiвноваги – це сiдловi точки функцiї
F (x,y) на X ×Y .
2. Перевiрити, що якщо елементи в матрицях виграшiв гравцiв зв’я-
занi наступними спiввiдношеннями
a
11
a
12
∧∨
a
21
a
22
,
b
11
>b
12
b
21
<b
22
,
то в грi не iснує рiвноваги Неша.
3. Перевiрити, що при виконаннi таких спiввiдношень в грi завжди
iснує двi рiвноваги Неша.
a
11
a
12
∨∧
a
21
a
22
,
b
11
>b
12
b
21
<b
22
.
4. Нехай гра має наступну структуру:
a
11
a
12
∨∨
a
21
a
22
,
b
11
>b
12
b
21
>b
22
.
Перевiрити, що при виконаннi таких спiввiдношень в грi завжди
iснує єдина рiвновага Неша.
5. Доведiть, що в антагонiстичнiй грi будь-яка ситуацiя оптимальна
за Парето.
6. Доведiть, що в грi
Γ зматрицями
A =
201
120
012
,B=
102
210
021
.
iснує єдина рiвновага Неша
(X
0
,Y
0
) = ((1/3,1/3,1/3),(1/3,1/3,1/3)).
157
7. Знайти всi рiвноваги Неша у грi Γ зматрицями
A =
51
34
,B=
52
14
.
8. Розв’язати бiматричнi iгри з наступними матрицями:
A
1
=
−10 2
1 −1
,B
1
=
5 −2
−11
;
A
2
=
−6 −1
−10 −3
,B
1
=
−6 −10
−1 −3
;
A
3
=
2 −1
−31
,B
3
=
1 −1
−32
;
A
4
=
−313
508
−441
,B
4
=
333
−220
−5 −30
.
2.10. ПОЗИЦIЙНI IГРИ
Означення 2.10.1. Позицiйна гра n гравцiв це:
1. Топологiчне дерево
G з видiленою вершиною, яка називається по-
чатковою позицiєю гри. Топологiчне дерево позицiйної гри – це
плоска фiгура, яка складається з вузлiв (позицiй гри) i направлених
вверх вiдрiзкiв, що з’єднують цi вузли. Кожен вузол з’єднується
лише з одним вузлом на нижчому рiвнi, кожний вiдрiзок означає
вибiр, який зробив гравець при даному ходi, i позначається номе-
ром, що вiдповiдає цьому вибору. Гiлка дерева – це ламана лiнiя,
що розпочинається в початковiй вершинi i йде вверх до кiнцевої
вершини дерева. Кожна гiлка вiдображає партiю гри.
2. Функцiя виграшу, що ставить у вiдповiднiсть кожнiй кiнцевiй по-
зицiї (вершинi) топологiчного дерева
G вектор (x
1
, ...,x
n
) iз R
n
,
координата
x
i
якого дорiвнює виграшу гравця i пiсля завершення
гри.
3. Розбиття множини всiх некiнцевих позицiй дерева
G на n +1 мно-
жин
S
0
,S
1
,...,S
n
, якi називаються множинами черговостi.Мно-
жина
S
i
складається з позицiй (вузлiв дерева), у яких вибiр (хiд)
робить гравець
i, 1 ≤ i ≤ n. Множина S
0
складається з позицiй, у
яких вибiр робиться випадково.
158
4. Розподiл ймовiрностей для кожної позицiї з S
0
на множинi насту-
пних позицiй.
5. Розбиття множини
S
i
для кожного i,i =1,...,n, на множини S
ij
,
якi називаються iнформацiйними множинами. Позицiї, що нале-
жать однiй iнформацiйнiй множинi, гравцем
i не розрiзняються.
(Немає достатньої кiлькостi iнформацiї для того, щоб їх розрiзни-
ти.)
6. Множина iндексiв
I
ij
та взаємно однозначне вiдображення множи-
ни
I
ij
на множину альтернатив кожної позицiї з S
ij
для кожної
iнформацiйної множини.
Означення 2.10.2. Позицiйна гра називається грою з повною iнформа-
цiєю,якщодлякожногогравця
i :1≤ i ≤ n, його iнформацiйнi множини
S
ij
складаються лише з однiєї точки.
Означення 2.10.3.Стратегiя
σ
i
гравця i –цефункцiя,щоставитьу
вiдповiднiсть кожнiй iнформацiйнiй множинi
S
ij
гравця деякий iндекс
з множини
I
ij
. Множину всiх стратегiй гравця будемо позначати через
i
.
Ми звикли до того, що гравець приймає рiшення про свiй вибiр лише
на кiлька крокiв наперед, навiть в той момент, коли вiн повинен зробити
вибiр. На практицi це так i є, тому що, наприклад, в таких iграх, як шахи
чи покер число можливих ходiв i варiантiв вибору настiльки велике,
що не можна заздалегiдь спланувати свої дiї, враховуючи всi можливi
обставини. Однак iз чисто теоретичної точки зору можна вважати, що
ще до початку гри кожний гравець вирiшив, як вiн буде дiяти в кожному
можливому випадку. Тобто ми вважаємо, що кожний гравець вибирає
певну стратегiю дiй ще до початку гри. Якщо це так, то залишається
лише зробити випадковi ходи.
Насправдi гравцiв цiкавлять не всi можливi стратегiї, а лише найкра-
щi, тобто тi, що максимiзують частки кожного гравця у виграшi (гравець
i намагається максимiзувати i-ту компоненту функцiї виграшу). Оскiль-
ки результати випадкових ходiв вiдомi лише як розподiли на множинi
виграшiв, то природно брати математичне сподiвання функцiї виграшiв,
яка визначена у випадку, коли гравцi використовують даний набiр стра-
тегiй.
Означення 2.10.4. Нормальна форма гри – це таблиця, що задає фун-
кцiю
π(σ
1
,...,σ
n
)={π
i
(σ
1
,...,σ
n
)}
n
i=1
на множинi всiх можливих зна-
чень змiнної
σ
i
∈
i
. Тут π
i
(σ
1
,...,σ
n
) – це математичне сподiвання
функцiї виграшу гравця
i при умовi, що гравцi застосовують стратегiї
σ
1
,...,σ
n
.
159
Приклад 2.10.1. Порiвняння монет. Гравець P
1
кладе на стiл монету.
Потiм гравець
P
2
кладе на стiл монету. Якщо монети лежать однако-
во, то гравець
P
1
платить гравцю P
2
одну одиницю. В iншому випадку
гравець
P
2
платить гравцю P
1
одну одиницю.
Iнформацiя, яку має гравець
P
2
:
а) гравець
P
2
не знає, як лежить монета гравця P
1
;
б) гравець
P
2
знає, як лежить монета гравця P
1
.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї грав-
цiв. Знайти нормальну форму гри.
У першому варiантi гри (гравець
P
2
не знає, як лежить монета грав-
ця
P
1
) кожен гравець має двi стратегiї – покласти монету вверх гербом
(позначається Г) чи решкою (позначається Р). Дерево гри зображено на
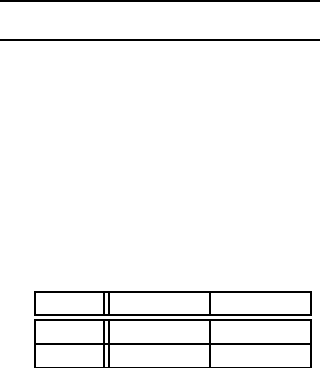
рис. 2.10.1. У кожного гравця одна iнформацiйна множина. У першо-
го вона складається з однiєї точки (початкова позицiя гри). Ця точка
обведена колом. У другого гравця iнформацiйна множина мiстить двi
точки (вони обведенi елiпсом). Нормальна форма гри задається табли-
H
H
H
H
H
H
H
H
@
@
@
@
@
@
@
@
@
@
(−1,1)(1,−1)(1,−1)(−1,1)
1
22
РГРГ
ГР
Рис. 2.10.1: Приклад 2.10.1 a)
цею 2.10.1. Рядки у таблицi вiдповiдають стратегiям першого гравця, а
стовпцi вiдповiдають стратегiям другого гравця.
Табл.2.10.1
Г Р
Г (−1,1) (1, − 1)
Р (1, − 1) (−1,1)
У другому варiантi гри (гравець P
2
знає як лежить монета гравця P
1
)
перший гравець має двi стратегiї – покласти монету вверх гербом чи ре-
160
