Научный вестник ДГМА 2009 № 01

Подождите немного. Документ загружается.

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

135

ПОТЕРИ ЭНЕРГИИ В ЧАСТОТНОМ ЭЛЕКТРОПРИВОДЕ С ВЕКТОРНЫМ

УПРАВЛЕНИЕМ И ФАЗЗИ-НЕЙРО КОРРЕКЦИЕЙ

Панкратов А. И., Побочий В. Г.

Рассматривается возможность повышения энергоэффективности частотного асин-

хронного электропривода с векторным управлением с фаззи-нейро коррекцией в динамиче-

ских режимах. Получен функционал энергозатрат в позиционном асинхронном электропри-

воде с векторным управлением с фаззи-нейро коррекцией. Рассмотрены составляющие по-

терь энергии в асинхроном электроприводе с векторным управлением при фаззи-нейро кор-

рекции. Получено решение задачи оптимизации функционала энергозатрат в общем виде.

В результате исследования функционала энергозатрат сделан вывод о возможности миними-

зации потерь энергии в частотном электроприводе с векторным управлением в динамических

режимах на основе фаззи-нейро коррекции.

Розглядається можливість підвищення енергоефективності частотного асинхронного

електропривода з векторним керуванням з фаззі-нейро корекцією в динамічних режимах.

Отримано функціонал енерговитрат у позиційному асинхронному електроприводі з вектор-

ним керуванням з фаззі-нейро корекцією. Розглянуто складові втрат енергії в асинхронному

електроприводі з векторним керуванням при фаззі-нейро корекції. Отримано рішення задачі

оптимізації функціонала енерговитрат у загальному вигляді. У результаті дослідження функ-

ціонала енерговитрат зроблено висновок про можливість мінімізації втрат енергії в частотному

електроприводі з векторним керуванням в динамічних режимах на основі фаззі-нейро корекції.

The possibility of power efficiency refinement of the vector control frequency electric drive

with fuzzy-neuro correction in dynamic regimes is considered. The functional of power inputs of

the vector control position electric drive with fuzzy-neuro correction is received. The components

of energy loss of the asynchronous vector control electric drive with fuzzy-neuro correction are

considered. The solution of the optimization problem of the functional of power inputs is received

in general form. The summary of investigation of the functional of power inputs which shows the

minimization possibility of energy loss of the vector control frequency electric drive in dynamic

regimes using fuzzy-neuro correction is given.

Панкратов А. И. канд. техн. наук, доц. кафедры АПП ДГМА

Paiss@yandex.ru

Побочий В. Г. аспирант ДГМА

Pobochiy@yahoo.com

ДГМА – Донбасская государственная машиностроительная академия

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

УДК 62-837

Панкратов А. И., Побочий В. Г.

ПОТЕРИ ЭНЕРГИИ В ЧАСТОТНОМ ЭЛЕКТРОПРИВОДЕ С ВЕКТОРНЫМ

УПРАВЛЕНИЕМ И ФАЗЗИ-НЕЙРО КОРРЕКЦИЕЙ

Современные системы векторного управления в настоящее время являются наиболее

распространенными среди систем электроприводов переменного тока. Они позволяют про-

сто и эффективно управлять такими сложными объектами как асинхронные двигатели (АД)

с короткозамкнутыми роторами, что позволяет существенно расширить область их примене-

ния. Развитие силовой электроники позволило создать надежные и относительно дешевые

преобразователи, а развитие быстродействующей микроэлектроники способствовало реали-

зации алгоритмов управления практически любой сложности. В настоящее время асинхрон-

ный векторный электропривод (АВП) является по существу техническим стандартом.

Однако, не смотря на то, что векторный способ управления с прямым управлением

моментом является достаточно экономичным, имеются резервы повышения энергоэффек-

тивности работы асинхронных электроприводов в динамических режимах.

Проблемам энергоэффективности управляемого электропривода (ЭП) на основе как

двигателя постоянного тока (ДПТ) так и АД посвящается большое количество работ. Многие

публикации [1, 2, 3] посвящены методам учета потерь в регулируемом и не регулируемом ЭП,

расчету энергопотребления ЭП, исследованию энергетических показателей ЭП. В некоторых

работах при анализе и расчете энергопотребления пренебрегают потерями в стали и механиче-

скими потерями, объясняя сложностью их определения. В работе [4] предложена оптимизация

позиционной электромеханической системы (ЭМС) на основе нейро-фаззи контроллера

Takagi-Sugeno. Применение нечеткого регулятора в режиме обратно-параллельной коррекции

сигнала задания позволяет для заданного быстродействия повысить энергоэффективность ЭП.

Целью работы является установление возможности минимизации потерь энергии

в динамических режимах в асинхронном электроприводе с векторным управлением и фаззи-

нейро коррекцией.

Потери в АД принято подразделять на две группы: электрические и механические [5].

Электрические потери состоят из потерь на намагничивание (потери в стали) и активных по-

терь (потери в меди). В общем виде потери энергии в АД, в переходных режимах, можно

представить в виде:

∫∫

Δ+Δ=Δ

пппп

мех

элп

dtPdtPA

, (1)

где

эл

PΔ – электрические потери;

мех

– механические потери;

пп

t – время переход-

ного процесса.

Таким образом, решение задачи минимизации потерь электромеханической энергии

заключается в оптимизации функционала (1).

Электрические потери в частотном ЭП с векторным управлением на примере позици-

онного ЭП в преобразованной системе координат x-y можно представить как:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

Δ+

⎟

⎠

⎞

⎜

⎝

⎛

=Δ

зпн

зп

зпн

зп

стyэл

RLM

212

7,03,01

)(

, (2)

где

– моментообразующая составляющая вектора тока статора АД;

R ,

R –

сопротивление фазы обмотки статора и приведенное сопротивление ротора АД;

L ,

M –

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

индуктивность фазы обмотки ротора и взаимная индуктивность обмоток статора и ротора

АД;

ст

PΔ – потери мощности в стали АД;

зпн

U ,

зп

U – номинальное и текущее значение

сигнала задания на перемещение.

Механические потери:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+Δ=Δ

15,0

пмехмех

, (3)

где

пмех

Δ – постоянные механические потери;

– номинальная и действую-

щая угловая скорости вращения вала АД.

Текущее значение сигнала задания на перемещение в позиционном ЭП при фаззи-

нейро коррекции формируется с учетом компенсирующих воздействий [5] по току

и скорости

, и определяется как:

iдIiyзпзп

FFIUU

++=

, (4)

где

F ,

– вектора соответствующих компенсирующих воздействий.

С учетом (2), (3), (4) преобразуем функционал (1) к виду:

[]

()

∫

+++++=Δ

пп

дyIдyIдy

дyп

dtKIKKIKKIKItA

ωωωω

ωω

, (5)

где коэффициенты подынтегрального выражения при соответствующих степенях рас-

считываются как:

212

3.01

)(

−

Δ+

⎟

⎠

⎞

⎜

⎝

⎛

зпнIiст

UFP

RLM

K ;

5.03.0

−−

Δ+Δ=

нпмехзпнiст

PUFPK

;

(

)

7.06.0

−−

+Δ=

зпнзпнзпIiстI

UUUFPK ;

(

)

7.06.0

−−

+Δ=

зпнзпнзпiст

UUUFPK

ωω

;

6.0

−

Δ=

зпнiIiстI

UFFPK

ωω

;

(

)

пмехзпнзпнзпзпст

PUUUUPK

5.07.03.0 Δ++Δ=

−−

Как видно из уравнения (5) подынтегральное выражение представляет собой нели-

нейную функцию двух переменных. Основное уравнение динамики ЭП имеет вид:

()

⎟

⎠

⎞

⎜

⎝

⎛

−ψ=−=

cyxпc

Jdt

311

, (6)

где J – момент инерции двигателя (механизма);

p – число пар полюсов АД;

– продольная составляющая потокосцепления ротора АД;

– момент сил статического

сопротивления.

Из уравнения (6) при векторном управлении по закону

const

получаем:

12 2

2122

п x

mconst

II K

JL p M

ωω

′

′′′

=⇒==. (7)

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

138

С учетом выше изложенных преобразований и допущений, выражение (5) приводится

к виду:

[]

()

∫

′

=Δ

′′

′

пп

ддIддIдд

ддп

dtKKKKKKKKKtA

ωωωωωωωω

ωωωω

. (8)

Подынтегральное выражение (8) представляет собой нелинейное дифференциальное

уравнение второго порядка.

Задача оптимизации функционала (8) сводится к решению вариационной задачи, на-

хождения экстремалей функционала:

),,(),,,(

211121 IIyy

CCtIICCt

ωω

на которых

функционал достигает экстремум [6].

Подынтегральное выражение в уравнении (8) может быть представлено в общем виде

уравнением Эйлера:

′

−

′

−

′′′′

ωωωωωω

FFFF

, (9)

где KKKKKKKKKF

ддIддIдд

′

′′

′

ωωωωωω

ωωωω

Уравнение Эйлера для (8) принимает вид линейного неоднородного дифференциаль-

ного уравнения:

022

''2

=−−

′

ωω

KKKK

дд

, (10)

или в виде:

ωω

KKKK

дд

=−

′

''2

. (11)

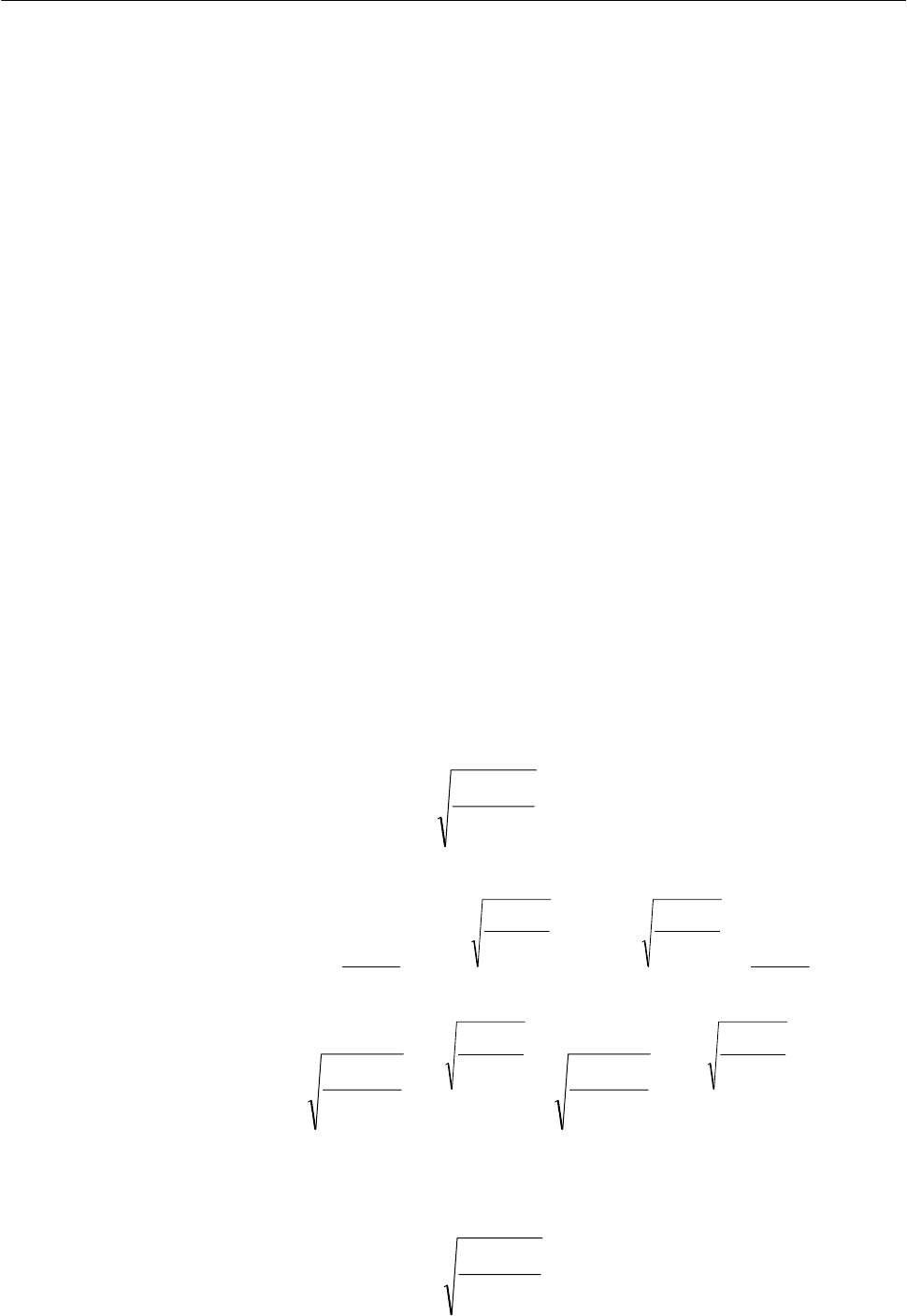
Решая уравнение (11) получаем выражения для экстремалей функционала (5) для двух

значений корней характеристического уравнения:

Корни действительные кратные:

2,1

′

±=

Уравнения экстремалей:

)(

2121

ωω

eCeC

eCeCt

tptp

−+=−+=

′′

−

(12)

⎟

⎠

⎞

⎜

⎝

⎛

−==

′′

−

′′

дy

KtKtI

)()(

ωω

. (13)

Выражение (13) получаем в соответствии с выражением (7).

Корни чисто мнимые кратные:

2,1

′

±=

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

139

Уравнения экстремалей:

( ) ( )

sincos

sincos)(

12211

ωω

tpCtpCt

−

























=−+=

′′

; (14)

























−













′′′

′′

KtKtI

дy

cossin)()(

ωω

ω . (15)

Задаваясь начальными условиями, определяются постоянные коэффициенты

2121

,,,

CCCC

ωω

. Полученные решения (12), (13), (14), (15) свидетельствуют о существо-

вании экстремума функционала (5).

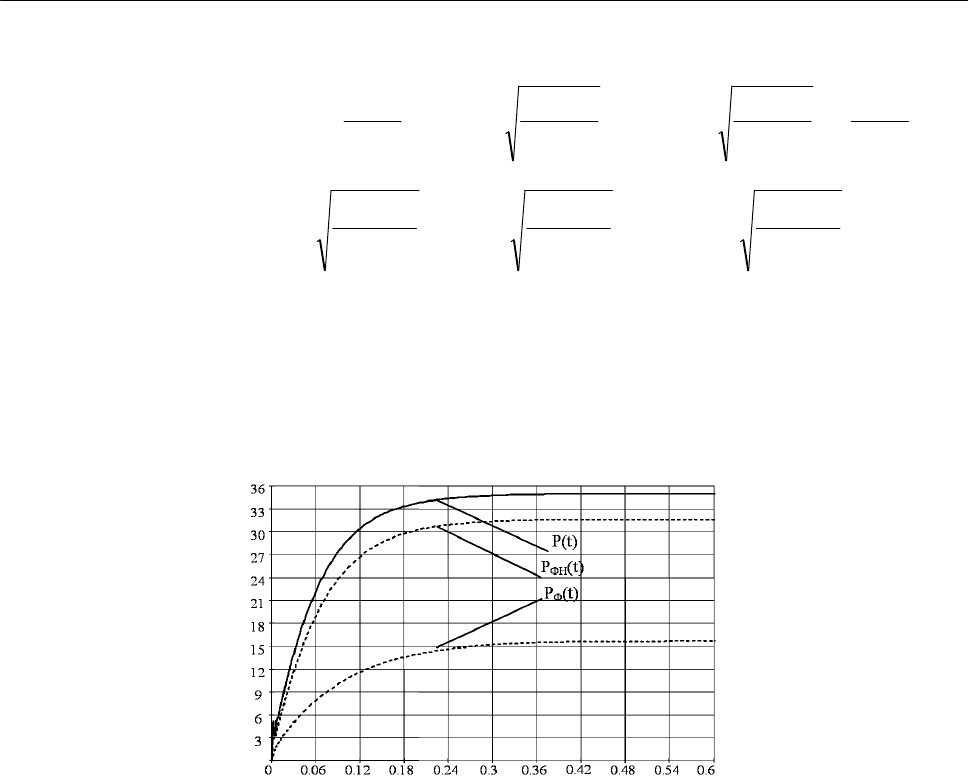
На рис. 1 представлена интегральная оценка мощности потерь при исследованиях по-

зиционного электропривода в Matlab без коррекции, при фаззи-нейро коррекцией и с фаззи

коррекцией.

Рис. 1. Интегральная оценка мощности потерь в асинхронном электроприводе без

коррекции (P(t)), при фаззи-нейро коррекции (P

ФН

(t)), при фаззи коррекции (P

(t))

ВЫВОДЫ

1. В результате исследования получен функционал, характеризующий потерю элек-

трической энергии в позиционном асинхронном электроприводе с векторным управлением.

2. Установлено существование возможности минимизации потерь электрической

энергии в динамических режимах на основе фаззи-нейро коррекции.

ЛИТЕРАТУРА

1. Толочко О. И. Расчет энергопотребления позиционного электропривода, реализующего оптималь-

ное по тепловым потерям управление / О. И. Толочко, П. И. Розкаряка // Наукові праці Донецького національно-

го технічного університету. – Донецьк : ДВНЗ «ДонНТУ». – 2007. – № 7 (128). – 307 с. – (Серія «Електротехні-

ка і енергетика»).

2. Андрющенко О. А. Метод учета потерь в асинхронном двигателе при векторном управлении. Про-

блемы автоматизированного электропривода. Теория и практика / О. А. Андрющенко, С. Б. Шевченко. – Одес-

са : «ОНПУ», 2006.

3. Браславский И. Я. Энергетическая оптимизация пусковых режимов частотных асинхронных элек-

троприводов. Проблемы автоматизированного электропривода. Теория и практика / И. Я. Браславский,

А. Я. Костылев, Д. П. Степанюк. – Одесса : «ОНПУ», 2006.

4. Панкратов А. И. Нейро-фаззи регулятор в системе позиционного электропривода / А. И. Панкра-

тов, В. Г. Побочий // Вісник Національного технічного університету «Харківський політехнічний інститут». –

Харків : НТУ «ХПІ». – 2008. – № 30. – 646 с.

5. Ключев В. И. Теория электропривода : учебник для вузов / В. И. Ключев. – М. : Энергоатомиздат,

1985. – 560 с.

6. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление / Л. Э. Эльсгольц . – М. :

Наука, 1969.

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

140

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРОМЕХАНИЧЕСКИХ КОЛЕБАНИЙ

В ДУГОВОЙ СТАЛЕПЛАВИЛЬНОЙ ПЕЧИ

Панкратов А. И., Шишкин А. В., Афанасьева А. В.

Рассмотрено влияние электродинамических усилий между гибкими кабелями трёх фаз

дуговой сталеплавильной печи при эксплуатационных коротких замыканиях на работу авто-

матических регуляторов мощности. Проведена оценка изменения взаимных индуктивностей

между гибкими кабелями трёх фаз. Установлено, что изменение взаимных индуктивностей

описывается законом затухающей синусоиды, а время свободных колебаний составляет 14 с,

это ухудшает стабильную работу печи. Создана модель электромеханических колебаний

гибких кабелей дуговой сталеплавильной печи. Данная модель позволяет учитывать эти воз-

мущающие воздействия. Получены графики мгновенных значений токов фаз при эксплуата-

ционном коротком замыкании. Оценка параметров автоколебаний позволит повысить каче-

ство регулирования мощности дуговой сталеплавильной печи. Результаты исследований мо-

гут быть использованы для всех электродуговых печей.

Розглянуто вплив електродинамічних зусиль між гнучкими кабелями трьох фаз дуго-

вої сталеплавильної печі при експлуатаційних коротких замиканнях на роботу автоматичних

регулювальників потужності. Проведено оцінку зміни взаємних індуктивностей між гнучки-

ми кабелями трьох фаз. Встановлено, що зміна взаємних індуктивностей описується законом

затухаючої синусоїди, а час вільних коливань складає 14 с, це погіршує стабільну роботу пе-

чі. Створена модель електромеханічних коливань гнучких кабелів дугової сталеплавильної

печі. Дана модель дозволяє враховувати ці обурюючи дії. Отримані графіки миттєвих зна-

чень струмів фаз при експлуатаційному короткому замиканні. Оцінка параметрів автоколи-

вань дозволить підвищити якість регулювання потужності дугової сталеплавильної печі. Ре-

зультати досліджень можуть бути використані для всіх електродугових печей.

Influence of fluctuations of electrodynamic forces between flexible cables of three phases of

an electric arc furnace at operational short circuits for work of automatic regulators of capacity. An

estimation of change of mutual inductances between flexible cables of three phases was got. It was

established, that change of mutual inductances is described by the law of a fading sinusoid, and time

of free fluctuations makes 14 sec., it worsens stable work of the furnace. Model of electromechani-

cal fluctuations of flexible cables of the electric arc furnaces is created. The given model allows to

consider these revolting influences. The charts of instantaneous values of phases currents at opera-

tional short circuit are got. The estimation of parametres of autovibrations will allow to raise quality

of capacity regulation of the electric arc furnace. Results of researches can be used for all electroarc

furnaces.

Панкратов А. И. канд. техн. наук, доц. кафедры АПП ДГМА

tm@dgma.donetsk.ua

Шишкин А. В. ассистент кафедры АПП ДГМА

Афанасьева А. В. аспирант ДГМА

ДГМА – Донбасская государственная машиностроительная академия

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

141

УДК 621. 365. 2

Панкратов А. И., Шишкин А. В., Афанасьева А. В.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРОМЕХАНИЧЕСКИХ КОЛЕБАНИЙ

В ДУГОВОЙ СТАЛЕПЛАВИЛЬНОЙ ПЕЧИ

При эксплуатационных коротких замыканиях (к. з.) возникают электродинамические

усилия между гибкими кабелями (г. к.) трёх фаз. После исчезновения эксплуатационных ко-

ротких замыканий г. к. начинают совершать свободные затухающие колебания. Расстояния

между фазами изменяются, что приводит к соответствующему изменению взаимных индук-

тивностей М

фаз. Поэтому в токах фаз возникают соответствующие модулированные зату-

хающие колебания. Сигналы изменения токов фаз отрабатываются автоматическими регуля-

торами мощности, которые стабилизируют электрические параметры короткой сети за счёт

изменения длин дуг. Т. о. электроды также начинают совершать продольные колебания, что

в результате приводит к колебаниям мощности цепи:

фф

SUI

⋅

где S – полная мощность для трёхфазной цепи;

U – фазное напряжение;

– ток

фазы.

Для расчета цепей ДСП разработаны различные подходы: замена дуги регулируемым

активным сопротивлением [1], при которой не учитывается нелинейность дуги; метод, пред-

ложенный С. И. Тельным [2], при котором мгновенные значения напряжения дуги за время

ее горения в каждом полупериоде принимаются равными постоянному значению, при этом

форма кривой напряжения дуги принята прямоугольной; метод гармонического анализа, за-

ключающийся в разложении напряжений и тока дуги в тригонометрический ряд [2, 3].

При моделировании электрических цепей ДСП ряд исследователей, например, Mon-

tanari G. C., Loggini M., Cavallini A., Varadan S., Makrwn E. B., Girgis A. A., Collantes R., Go-

mez T., применяют стохастические модели для описания работы дуговых электропечей, опи-

раясь, на первый взгляд, на случайный характер нагрузки [4-6]; альтернативным подходом

описания нестационарного характера нагрузки является применение детерминированного

хаоса исходя из присутствия хаоса в токе дуги, который исследовали O’ Neill-Carrillo E.,

Heydt G., Kostelich E. J., Jang G., Wang W., Heydt G. T. [7, 8].

Целью работы является моделирование трёхфазной электрической сети дуговой стале-

плавильной печи на примере трёхфазной дуговой 12-ти тонной печи ДСП-12Н3 ЗАО «НКМЗ».

В данной работе для расчёта цепей с дугами используется методика, основанная на

применении нелинейных дифференциальных уравнений, которые позволяют более точно и

реалистично описывать поведение электрических цепей с дугами [9]. Активные и реактив-

ные сопротивления фаз короткой сети принимаются независимыми от тока. А сопротивления

дуг, как нелинейных элементов, принимаются переменными, зависимыми от тока [10, 11].

Подина печи является непроводящей и сопротивление между нулевыми точками печи

и трансформатора равно бесконечности, поэтому соблюдается условие () () () 0

ABC

it it it++=

(I закон Кирхгофа).

В работе вольтамперная характеристика (ВАХ) дуги задаётся дифференциальным

уравнением, что позволяет учесть влияние параметров электрического контура печи и усло-

вий горения дуг на форму ВАХ [11].

Математическая модель, учитывающая электродинамические воздействия между фа-

зами гибких кабелей, для трёхфазной цепи, соединённой в «звезду», каждая фаза которой

содержит электрическую дугу, представляет систему дифференциальных уравнений:

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

142

()

() () ()

() () () () ();

()

() () ()

() () () () ();

()

() ()

() () () ()

AB A

A A A A AB AC

BA B

B B B B AB BC

C СС CAC CB

di t

di t di t i t

Ut rit L M t M t ut

dt dt dt g t

di t

dit dit it

Ut rit L M t M t ut

dt dt dt g t

di t i

di t di t

Ut rit L M t M t

dt dt dt

=+ + + ++

=+ + + +

()

();

()

() () () 0; (1)

()

;

()

;

()

ABC

C д

it it it

dg t

dt g t

dg t

dt g t

dg t U

dt g t

⎪

++=

⎨

⎪

−

⎪

−

⎪

−

⎪

⎩

где (), ()

UtUt и ()

Ut – фазные напряжения с низкой стороны трансформатора;

r ,

L ,

L – суммарные эквивалентные активные сопротивления и индуктивно-

сти фаз трансформатора, приведенные ко вторичной стороне трансформатора;

(), ()

AB BC

tM t и ()

t – переменные взаимные индуктивности между фазами;

Aэл

r ,

Bэл

r ,

Cэл

– сопротивления электродов фаз;

(), ()

it it

()

– мгновенные значения токов фаз, А;

() ()

it it

gtgt

()

– мгновенные значения напряжений дуг, В;

()ut – мгновенное сме-

щение нулевой точки печи относительно нуля трансформатора, которое определяется из сис-

темы уравнений (1).

Для учёта возмущающих воздействий необходимо определить законы колебаний гиб-

ких кабелей трёх фаз дуговой электросталеплавильной печи при возникновении эксплуата-

ционных коротких замыканий и найти зависимости изменения взаимных индуктивностей

между гибкими кабелями фаз.

Для определения законов

колебаний гибких кабелей в первом приближении предста-

вим их в виде математических круговых маятников.

В ходе исследований были получены выражения взаимных индуктивностей между

гибкими кабелями, изменяющиеся вследствие действия к. з. в фазе В.

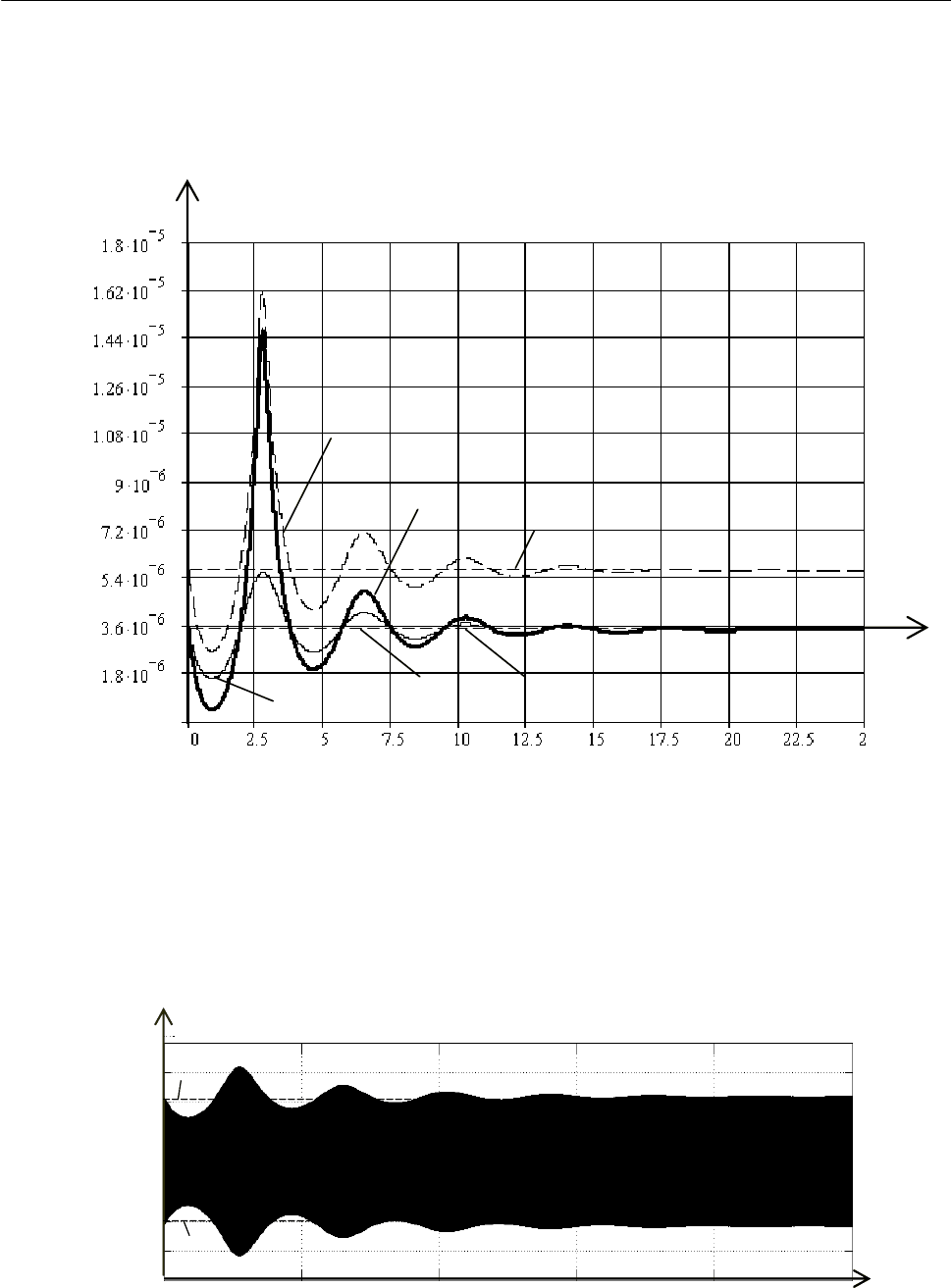
На рис. 1 приведены графики зависимостей взаимных индуктивностей между гибкими

кабелями в состоянии их свободных колебаний при к. з. в фазе В, полученные в результате

исследований.

Из рис. 1 видно, что время свободных колебаний составляет приблизительно 14 с.

Амплитуды колебаний взаимных индуктивностей между гибкими кабелями в состоянии сво-

бодных колебаний для дуговой сталеплавильной печи ДСП-12 равны

2, 046 10 , 0, 973 10

−−

⋅⋅

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

143

1, 053 10

−

⋅

Гн между фазами А и В, В и С, и А и С соответственно. Наиболее ярко выраже-

но изменение взаимной индуктивности между фазами А и С, т. к. между этими фазами рас-

стояние меньше, чем между двумя другими парами фаз.

Гн

t , с

(

)

(

)

(

)

Рис. 1. Графики зависимостей взаимных индуктивностей между гибкими кабелями

в состоянии их свободных колебаний при к. з. в фазе В

На рис. 2 представлены графики мгновенных значений токов фазы А при эксплуата-

ционном к. з. в фазе В ДСП-12Н3 ЗАО «НКМЗ», полученные в программной среде MatLab

Simulink. Графики мгновенных значений токов для двух других фаз имеют подобный вид.

Рис. 2. Графики мгновенных значений токов фазы А при эксплуатационном к. з.

в фазе В ДСП-12Н3 ЗАО «НКМЗ»

t, с

(), 10

it A×

15 20

-1

-2

-3

-4

mн

−

НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (4Е), 2009

144

Из рис. 2 можно сделать вывод, что время свободных колебаний составляет 14 с, как

и время колебаний взаимных индуктивностей фаз. Максимальная глубина модуляции токов

по числовым данным составляет:

max

11098

100% 100% 53,7%;

20650

=⋅=⋅=

max

7440

100% 100% 36%;

20650

=⋅=⋅=

(2)

max

12597

100% 100% 61%,

20650

=⋅=⋅=

где

max А

max B

max C

IΔ

– перерегулирование токов в фазах А, В и С;

m н

– ампли-

тудное номинальное значение тока в каждой фазе.

Такие возмущения приводят к ухудшению стабильной работы печи, перерасходу

электроэнергии, поломке электродов, увеличению времени расплавления металла и сниже-

нию производительности печи.

ВЫВОДЫ

В работе было установлено, что изменения взаимных индуктивностей между фазами

вследствие эксплуатационных к. з. приводят к нарушению стабильностей токов дуг и работы

автоматических регуляторов мощности ДСП. Поэтому необходимо разработать такие регу-

ляторы мощности, которые позволили бы учитывать и исключать данные возмущающие воз-

действия.

ЛИТЕРАТУРА

1. Свенчанский А. Д. Электрические промышленные печи : дуговые печи и установки специального на-

грева : учебник для вузов / А. Д. Свенчанский, И. Т. Жердев, А. М. Кручинин и др. ; под ред. А. Д. Свенчанского. –

2-е изд., перераб. и доп. – М. : Энергоиздат, 1981. – 296 с., ил.

2. Карпенко С. В. Разработка математической модели и компьютерной

системы для исследования

трёхфазных цепей с электрическими дугами / С. В. Карпенко, В. Д. Сарычев, С. П. Мочалов // Известия высших

учебных заведений. Чёрная металлургия. – 2006. – № 6. – С. 48–51.

3. Сисоян Г. А. Электрическая дуга в электрической печи. 3-е изд / Г. А. Сисоян. – М. : Металлургия,

1974. – 304 с.

4. Montanari G. C., Loggini M., Cavallini A. e. a. // IEEE Transactions on Power Delivery. – 1994. – V. 8. –

№ 4. – P. 2026–2036.

5. S. Varadan, E. B. Makrаwn, A. A. Girgis // IEEE Transactions on Power Delivery. – 1996. – V. 1. – № 3. –

P. 1685–1691.

6. R. Collantes, T. Gomez // IEEE Transactions on Power Delivery. – 1997. – V. 12. – № 4. – P. 1812–1817.

7. O’Neill-Carrillo E., Heydt G., Kostelich E. J. e. a. // IEEE Transactions on Power Delivery. – 1999. – V. 14. –

№

2. – P. 537–542.

8. Jang G., Wang W., Heydt G. T. e. a. // IEEE Transactions on Power Delivery. – 2001. – V. 29. – № 11. –

P. 1060–1073.

9. Acha E., Semlyen A., Rajakovich N. // IEEE Transactions on Power Delivery. – 1990. – V. 5. – № 3. –

P. 1390–1395.

10. Игнатов И. И. Расчёт электрических параметров и режимов дуговых сталеплавильных печей /

И. И. Игнатов, А. В. Хаинсон // Электричество. – 1983. – № 8.

11. Игнатов И. И. Математическое моделирование электрических режимов дуговых сталеплавильных

печей / И. И. Игнатов, А. В. Хаинсон // Электричество. – 1985. – № 8.