Непейвода Н.Н. Прикладная логика

Подождите немного. Документ загружается.

4.4. РАВЕНСТВО

Например, поскольку треугольники, имеющие одни и те же верши-

ны, отождествляются, мы не можем в геометрическиx доказательствах

различать иx тем, что у одного сначала была проведена сторона AB, а

затем AC, а у другого — наоборот. Способ, которым они были начерче-

ны, роли уже не играет.

Следовательно, имеет место следующий основной закон равенства:

Если

A — произвольная формула языка нашей

формальной теории, то

∀x, y (x = y ⇒ (A(x) ⇒ A(y))) .

(4.26)

Другими словами, свойства равных объектов эквивалентны. Несколько

неточно выражаясь, равные объекты обладают одинаковыми свойства-

ми. Г. Лейбниц превратил это свойство равенства в его содержательное

определение:

Два предмета равны,

если они обладают одинаковыми свойствами.

Но эти два предмета не могут обладать всеми одинаковыми свойствами,

поскольку уже в формулировке Лейбница они различаются. Поэтому на

современном математическом языке формулировку Лейбница записы-

вают в виде формулы, не укладывающейся в наш стандартный язык ло-

гики:

∀P (P (x) ⇔ P (y)) ⇔ x = y. (4.27)

Здесь

P — переменная по предикатам

Таким образом,в математическом утверждении можно заменить рав-

ные объекты друг на друга, и мы получим эквивалентное утверждение.

Например, утверждение, говорящее о числе “4”, мы можем заменить

на эквивалентное утверждение, говорящее о выражении “2 + 2”. Но в

обычном языке не всегда так. Можно сказать, что «Вовочка не знал, что

Это внешне безобидное расширение языка сразу же было предложено авторами язы-

ка логики, но уже один из них — Б. Рассел — заметил глубоко спрятанные сложности

при рассмотрении кванторов по предикатам. А сейчас стало известно, что в языке с

кванторами по предикатам легко сформулировать утверждение, истинность которого

эквивалентна неразрешимой математической проблеме. Доказано также, что для такого

расширения языка не может быть полной системы формальных доказательств, которая

имеется в обычной логике и рассматривается далее в нашем пособии.

ГЛАВА 4. МЕТОДЫ ПЕРЕВОДА

2+2 —это четыре»,но нельзя — «Вовочка не знал,что 2+2 —это 2+2».

Высказывания, выдерживающие замену равных,называются экстенси-

ональными. Иногда свойство экстенсиональности содержательно ком-

ментируют как зависимость высказывания лишь от объема входящих в

него понятий, но не от их содержания. Соответственно, высказывания,

меняющие значение для равных объектов, называются интенсиональ-

ными, зависящими от содержания.

Еще одно свойство равенства:

∀x(x = x), (4.28)

т. е. каждый объект равен самому себе.

Из этиx двух свойств равенства выводятся другие законы равенства,

например,

∀x, y, z (x = y & y = z ⇒ x = z) ; (4.29)

∀x, y (x = y ⇒ y = x) ; (4.30)

∀x, y, z (x = y & x = z ⇒ y = z) . (4.31)

Докажем для образца (4.29): если первый предмет равен второму, а

второй — третьему, то первый предмет равен третьему. В самом деле,

пусть при конкретных произвольных x, y, z, выполнено x = y и y = z.

Тогда, по основному свойству равенства (4.26) в x = y можно y заме-

нить на z, и получим x = z, что и требовалось доказать.

Исключительно важную роль в языке математики играет утвержде-

ние о единственности

x,удовлетворяющего данному условию A (напри-

мер, часто приходится доказывать, что решение задачи единственно).

На самом деле обычно подразумевается не только то, что решение

задачи единственно, но и то, что она имеет решение, т. е. доказывается

не только единственность, а существование и единственность объекта,

удовлетворяющего свойству

A. При аккуратных формулировках это не-

обходимо оговаривать.

Единственность “в чистом виде” выражается следующим образом:

∀x, y(A(x) & A(y) ⇒ x = y). (4.32)

Это утверждение воспроизводит сплошь и рядом встречающийся в ма-

тематике метод доказательства единственности. Нужно доказать,что ре-

4.4. РАВЕНСТВО

шение задачи единственно. «Рассуждаем от противного

.Пусть есть два

различных x, y, являющихся решениями данной задачи. Тогда... Итак,

мы доказали, что x = y, и полученное противоречие доказывает теоре-

му

».

Заметим, что утверждение «

, удовлетворяющее

, единственно»,

вообще говоря, не предполагает, что оно существует, что задача вооб-

ще имеет решение. Чисто формально, по таблицам истинности, (4.32)

истинно и в том случае, когда

x, удовлетворяющих A, вообще нет. По-

этому (4.32) точнее читать «есть не более одного x, удовлетворяющего

A(x)».

То же высказывание можно выразить и многими другими форму-

лами, часть которых приведена в упражнениях. Мы выбрали наиболее

выразительную.

А утверждение «задача имеет единственное решение», «существует

единственное x, такое, что A(x)» выражается в форме

∃x A(x) & ∀x, y (A(x) & A(y) ⇒ x = y) . (4.33)

Но (4.33) не самая выразительная запись утверждения о единственно-

сти. Гораздо выразительнее

∃x ∀y(A(y) ⇔ x = y). (4.34)

Итак, то, что существует единственное

x, удовлетворяющее A(x),

означает, что условие A(x) на самом деле сводится к равенству этому

единственному x.

Сказать, что точка x является центром окружности, описанной око-

ло треугольника ABC, то же, что сказать, что она совпадает с точкой

Q, построенной при доказательстве теоремы о том, что вокруг любого

треугольника можно описать окружность, и притом только одну.

А теперь наступает черед высказываний типа «существует n такиx

x, что A(x)», «существует не менее n такиx x, что A(x)», «есть не более

n такиx x, что B(x)», где n заранее дано.

Общий способ получить утверждение «существует не более n такиx

x, что A(x)»:

∃x

, . . . , x

(∀y (A(y) ⇔ x

= y ∨ ∙∙∙ ∨ x

= y)) . (4.35)

Эта фраза, которую обычно здесь произносят, на самом деле лишняя, мы просто

предполагаем условие утверждения о единственности.

Эта фраза также лишняя, мы просто доказали заключение импликации.

ГЛАВА 4. МЕТОДЫ ПЕРЕВОДА

Но здесь мы не утверждаем, что этиx различных x ровно n: если x и y

обозначены по-разному, то это отнюдь не означает, что они принимают

различные значения: они имеют право принимать разные значения, но

имеют право принять и одинаковые.

Итак, мы приходим к необходимости уметь формулировать разли-

чие, чего мы пока тщательно избегали в основном тексте.

Если

x = y означает равенство, неразличимость, совпадение пред-

метов, то соответственно

(x = y)

, обычно обозначаемое x 6= y, —

иx различие. Итак, сказать, что есть не менее двух различных решений

задачи, очень просто:

∃x, y (x 6= y & A(x) & A(y)) . (4.36)

Так же просто сказать и то, что иx ровно два:

∃x, y (x 6= y & ∀z(A(z) ⇔ z = x ∨ z = y)) . (4.37)

А для большего числа решений уже начинаются сложности. Сказать, в

частности, что

x 6= y & y 6= z — недостаточно. Ответьте сами, поче-

му? Возникает следующее выражение, которое употребляется при точ-

ных формулировках вместо расплывчатого «x

, . . . , x

различны»: «все

, . . . , x

попарно различны», что переводится в виде длинной конъ-

юнкции различий:

6= x

& x

6= x

& . . . & x

6= x

& x

6= x

& . . . & x

6= x

. . .

& x

n−1

6= x

(4.38)

А теперь мы уже готовы формулировать различные высказывания о ко-

личестве элементов, удовлетворяющих

A, при условии, если это коли-

чество задано заранее.

Часто употребляются следующие сокращения:

“Существует единственное

x,такое,что A(x)”:∃1xA(x) либо ∃!xA(x)

“Существует ровно n такиx x, что A(x)”: ∃

x A(x)

“Существует не менее n такиx x, что A(x)”: ∃

xA(x)

“Существует не более n такиx x, что A(x)”: ∃

xA(x)

4.4. РАВЕНСТВО

Подытожим:

Определение равенства, данное Лейбницем, применяется в

двух направлениях: оно позволяет перенести свойства одно-

го объекта на другой, если доказано их равенство; оно заста-

вляет нас ограничивать математический язык таким обра-

зом,чтобы не допускать формулировку свойств,которые мо-

гут не сохраняться для равных объектов (интенсиональных).

В математический язык можно корректно вводить формули-

ровку, говорящую, что имеется данное фиксированное чи-

сло элементов, удовлетворяющих некоторому условию. Ес-

ли это число не фиксировано, то утверждение может вый-

ти за рамки чистого языка логики, но остается математиче-

ским.

Предикат

= имеет особый статус в логике.

Если ∃1x A(x),то ограниченные кванторы ∀x(A(x) ⇒ B(x))

и ∃x(A(x) & B(x)) совпадают по значению.

Упражнения к § 4.4

4.4.1. В нашем классе есть единственный отличник.

4.4.2. В нашем классе ровно три отличника.

4.4.3. Если два философа сидят за одним столом, то они обязательно

начинают спорить.

4.4.4. Стоят три женщины у колодца и не разговаривают.

4.4.5. В нашем цехе никто, кроме Иванова, Петрова, Васильева и Сидо-

рова, не умеет играть в домино.

4.4.6. У уравнения

−5x

+ 4x = 0 нет решений, отличных от 0, ±1,

±2.

4.4.7. У уравнения

+ bx + c + ε sin x = 0 ровно два решения.

4.4.8. У уравнения

+ bx + c + ε sin x = 0 не более трех решений.

4.4.9. У уравнения

+ bx + c + ε sin x = 0 не менее трех решений.

ГЛАВА 4. МЕТОДЫ ПЕРЕВОДА

Перевести на естественный язык.

4.4.10.

∃x, y, z (

(x) &

(y) &

(z) & x 6= y & y 6= z & x 6= z) ⇒ ∀x

(x).

(x) — “x знает тайну”.

4.4.11.

∀x(x 6= a & x 6= b ⇒ f (x) 6= 0).

4.4.12.

∀x(f(x) = 0 ⇒ x = a ∨ x = b).

4.4.13.

∃x, y ∀z(

(

, z) ⇒ z = x ∨ z = y).

— Ваня,

— дружит.

4.4.14.

∃x, y (

(

, x) &

(

, y) & ∀z(z 6= x & z 6= y ⇒

(

, z))).

Обозначения те же, что и в 4.4.13.

4.4.15.

∀x (

(x) ⇒ ∃y (

(y) & ∀z (

(x, z) &

(z, x) ⇔ y = z))).

(x) — “x – человек”,

— любить.

4.4.16.

∀x, y, z(x 6= y & y 6= z & x 6= z ⇒ f(x) 6= 0 ∨ f(y) 6= 0 ∨ f(z) 6= 0).

4.4.17.

∀x(

(x) ⇒ ∀y(x 6= y ⇒

(y))).

— “быть чемпионом”.

4.4.18.

∃x (

(x) & ∀y(

(y) ⇒ y = x)).

Обозначение то же, что в 4.4.17.

4.4.19.

∀x ∀y ∀z(x ∈ X & y ∈ X & z ∈ X ⇒ x = y ∨ y = z ∨ x = z).

4.4.20. Можно ли использовать выражение (4.35) для перевода выска-

зывания “Может быть не больше

n таких x, что A(x)?” Если нет,

то почему?

§ 4.5. ТАБЛИЦЫ ИСТИННОСТИ

И ФОРМУЛИРОВКА ОТРИЦАНИЙ

Здесь мы коснемся двух инструментов,применяемых в современной ма-

тематике и ее приложениях на много порядков чаще других методов ма-

тематической логики. Это связано не столько с их полезностью и важ-

ностью, сколько с их простотой.

Как следует из соглашения 3, если формула не содержит кванторов

и переменных, то ее значение полностью определяется конечным на-

бором значений элементарных формул, из которых она построена. Если

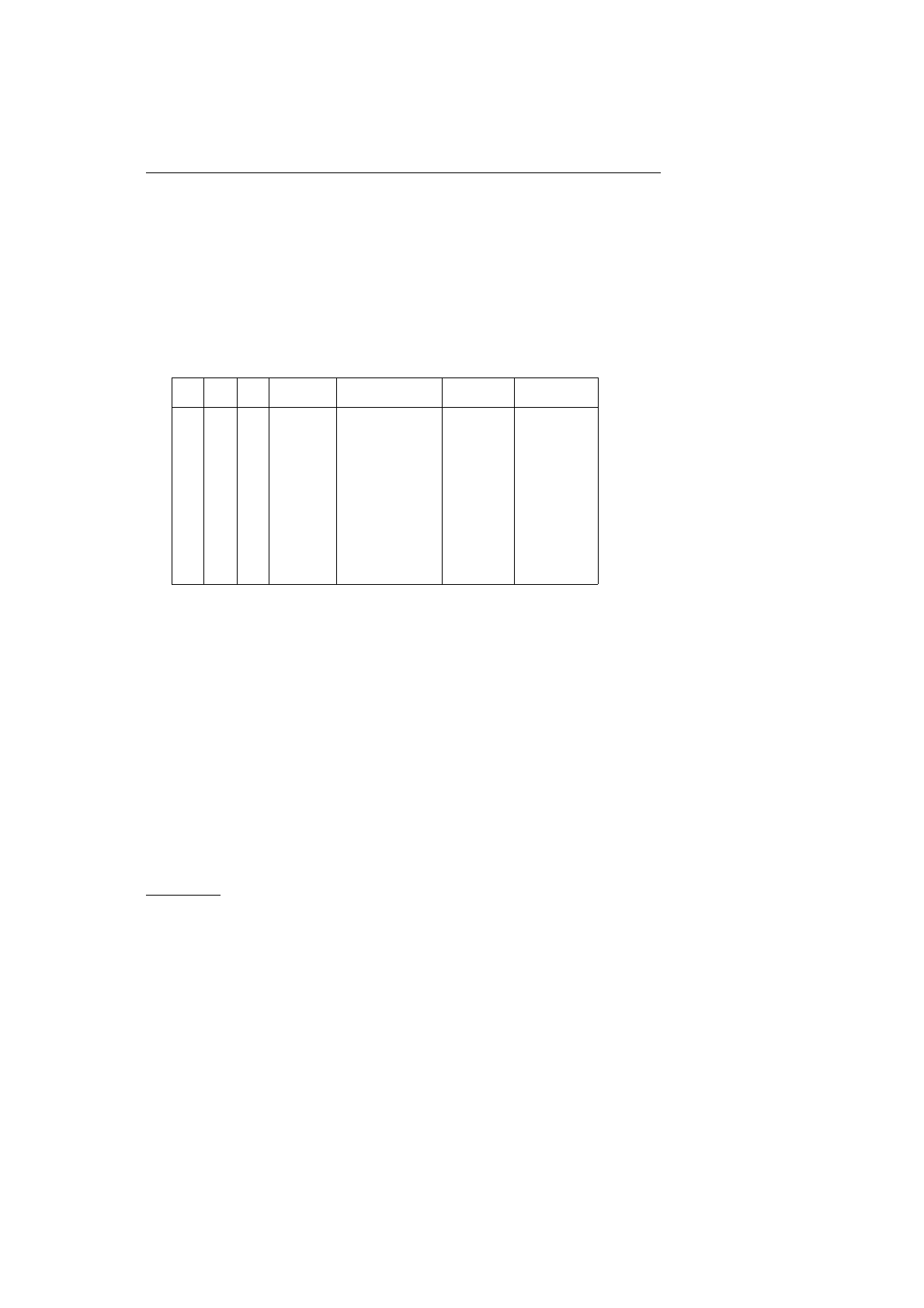
4.5. ФОРМУЛИРОВКА ОТРИЦАНИЙ

таких строительных блоков n, то достаточно перебрать 2

их значений

чтобы выяснить характер зависимости значения формулы от значений

ее компонент. Систематический перебор всех вариантов значений эле-

ментарных блоков и вычисление для них значений формулы и дает та-

блицу истинности. Рассмотрим пример. Построим таблицу истинности

для формулы

(A ⇒ B ∨ C) ⇒ (A ⇒ B) .

A B C B ∨ C A ⇒ B ∨ C A ⇒ B Формула

1 1 1 1 1 1 1

1 1 0 1 1 1 1

1 0 1 1 1 0 0

1 0 0 0 0 0 1

0 1 1 1 1 1 1

0 1 0 1 1 1 1

0 0 1 1 1 1 1

0 0 0 0 1 1 1

(4.39)

Здесь видно, что, перебрав восемь возможных приписываний значе-

ний переменным, мы отыскали то единственное, при котором формула

ложна. Если бы такового не оказалось, то формула могла бы считаться

логически истинной и применяться практически не глядя на интерпрета-

цию

, а уж в обычной математике вообще безусловно. Поэтому в логике

в особенности интересуются формулами,тождественно истинными при

любой интерпретации, и дали им особое название

— тавтологии. То,

что формула A является тавтологией, будем обозначать в данной гла-

ве |= A. Особое место среди тавтологий занимают эквивалентности —

тавтологии вида A ⇔ B. Установленная эквивалентность дает возмож-

ность повсюду заменять выражения A и B друг на друга

Тавтологии и противоречия важны для логики потому, что они не

зависят от конкретной формализации предметной области. Далее, при-

А почему 2

? Докажите.

Лишь бы была применима сама классическая логика.

Правда, не очень почтительное.

Данное свойство — свойство замены эквивалентных — будет подробнее рассмотре-

но далее.

ГЛАВА 4. МЕТОДЫ ПЕРЕВОДА

менение тавтологий дает общие средства вывода следствий и преобра-

зования формул. И, наконец, для проверки тавтологичности в классиче-

ской логике имеется достаточно эффективный во многих содержатель-

ных случаях метод — семантические таблицы, которым посвящена це-

лая глава

Определение 4.5.1.

Замкнутые формулы, не содержащие кванторов,на-

зываются

пропозициональными

; подъязык логики предикатов, состоя-

щий из пропозициональных формул, —

пропозициональным

языком или

языком

логики высказываний

Оценивание

пропозициональной форму-

лы — функция,сопоставляющая всем ее различным элементарным под-

формулам

истину

либо

ложь

Таблица истинности

— функция, сопо-

ставляющая каждому возможному оцениванию значение формулы при

этом оценивании.

Поскольку элементарных подформул у формулы конечное число и

каждая из них может принимать лишь два значения, составление табли-

цы истинности — конечная процедура.

Предложение 4.5.1. Пропозициональная формула является тавтоло-

гией тогда и только тогда, когда ее таблица истинности является

функцией, тождественно равной истине. Она является противоречи-

ем, если таблица тождественно равна лжи.

§ 4.6. ПРОСТЕЙШИЕ ПРЕОБРАЗОВАНИЯ

КЛАССИЧЕСКИХ ФОРМУЛ

Уже простейшие тавтологии позволяют развить полезные преобразова-

ния формул классической логики и, соответственно,математики.Для их

установления достаточно построить простейшую таблицу истинности в

пропозициональном случае либо обратиться к определению истинности

в предикатном. Перечислим их.

A ∨ ¬A (4.40)

¬¬A ⇔ A (Закон двойного отрицания) (4.41)

Наличие метода проверки является необходимым условием практической примени-

мости формализма.

4.6. ПРОСТЕЙШИЕ ПРЕОБРАЗОВАНИЯ

¬(A ∨ B) ⇔ (¬A & ¬B) (Закон де Моргана) (4.42)

¬(A & B) ⇔ (¬A ∨ ¬B) (Закон де Моргана) (4.43)

¬(A ⇒ B) ⇔ (A &

B) (4.44)

¬(A & B) ⇔ (A ⇒ ¬B) (4.45)

¬(A ⇔ B) ⇔ (A ⇔ ¬B) (4.46)

¬∀x A(x) ⇔ ∃x ¬A(x) (4.47)

¬∃x A(x) ⇔ ∀x ¬A(x) (4.48)

(A ⇒ B) ⇔ (¬B ⇒ ¬A) (Закон контрапозиции) (4.49)

(A ⇔ B) ⇒ (A & C ⇔ B & C) (4.50)

(A ⇔ B) ⇒ (A ∨ C ⇔ B ∨ C) (4.51)

(A ⇔ B) ⇒ (¬A ⇔ ¬B) (4.52)

(A ⇔ B) ⇒ ((A ⇒ C) ⇔ (B ⇒ C)) (4.53)

(A ⇔ B) ⇒ ((C ⇒ A) ⇔ (C ⇒ B)) (4.54)

∀x(A ⇔ B) ⇒ (∀x A ⇔ ∀x B) (4.55)

∀x(A ⇔ B) ⇒ (∃x A ⇔ ∃x B) (4.56)

A & B ⇔ B & A (4.57)

A ∨ B ⇔ B ∨ A (4.58)

Эти тавтологии используются при обосновании двух важнейших пре-

образований формул: формулировке отрицаний и замене эквивалент-

ных.

Алгоритм формулировки отрицаний. Под формулировкой отри-

цаний подразумевается эквивалентное преобразование формулы

¬A та-

ким образом, чтобы операция отрицания применялась лишь к элемен-

тарным формулам. Тавтологии (4.40)–(4.58) приводят к следующему ал-

горитму.

Базис рекурсии.

Если мы пришли к элементарной формуле, оставля-

ем перед ней отрицание и заканчиваем работу.

Шаг 1.

Если A есть (B ∨ C), заменяем ∨ на & и формулируем отри-

цания B, C.

Шаг 2.

Если A есть (B & C) {(B ⇒ C)}, заменяем & либо ⇒ друг

на друга, формулируем отрицание заключения C, оставляя посылку B

без изменения.

Шаг 3.

Если A есть ¬B, отбрасываем оба отрицания и оставляем B

без изменения.

ГЛАВА 4. МЕТОДЫ ПЕРЕВОДА

Шаг 4.

Если A есть ∀x B {∃x B}, то заменяем кванторы друг на дру-

га и формулируем отрицание B

Итак, при формулировке отрицаний достаточно большие части фор-

мул, происшедшие из посылок импликаций либо переходящие в них,

остаются неизменными. Конечно же, для соблюдения математического

стиля целесообразно порой заменять и элементарные формулы, напри-

мер, взаимно превращая

< и >. Но более важно другое замечание, ис-

ходящее из известной неоднозначности переводов между содержатель-

ным и формальным языком. Изучая тавтологии, на которых мы базиру-

емся, можно отметить, что по крайней мере для конъюнкции & имеется

больше одного варианта переводов

. Поэтому имеется и другой вари-

ант формулировки отрицания &: заменить конъюнкцию на дизъюнкцию

и сформулировать отрицания обеих частей. В частности, для предложе-

ния «Все ораторы честолюбивы и скучны», переводящегося

∀x (

Оратор

(x) ⇒

Честолюбив

(x) &

Скучен

(x)) ,

лучше вариант формулировки отрицания с ∨.

Формулировка отрицания иногда является также шагом проверки

переводов на формальный язык и выбора из них более приемлемого.

Например, многие студенты замечают, что в утверждении про ящеров

(4.19) отношение пожирания на самом деле антисимметрично («Волки

от испуга скушали друг друга» — указание на крайне неординарную си-

туацию; кстати, переведите и это предложение) и можно заменить

∨ на

⊕:

∀x (

(x) ⇒ ∃y (

(y) & (

(x, y) ⊕

(y, x)))) . (4.59)

В нашем конкретном мире это утверждение практически совпадает по

истинностному значению с исходным, но вот насчет их отрицаний см.

упражнение 4.6.5.

Рассмотрение предложения (4.23) и его перевода (4.24) приводит к

еще одному интересному наблюдению. При переходе к содержательно-

Чтобы подчеркнуть чисто синтаксический характер этого преобразования и то, что

оно никак не влияет на переменную квантора, записываем подкванторное выражение

без ссылок на связанную квантором переменную.

В классической логике они эквивалентны, и выбор между ними прежде всего вопрос

вкуса. Но, как и обычно, стилистическое различие в классической логике переходит в

семантическое в неклассических.