Непейвода Н.Н. Прикладная логика

Подождите немного. Документ загружается.

8.5. ЯЗЫКИ ВЫСШИХ ПОРЯДКОВ

211

Теперь хотелось бы дать синтаксический метод проверки логического

следования, но доказано, что полной формализации не может быть уже

для языка второго порядка, включающего лишь переменные по преди-

катам, аргументами которых являются объекты. Более того, если тео-

рема полноты показала, что понятие общезначимости в классической

логике предикатов определяется полностью и однозначно, то здесь по-

является глубоко скрытая, зато неустранимая, неоднозначность. Уже в

логике второго порядка появляются формулы, общезначимость которых

зависит от неразрешимых проблем современной математики и теории

множеств. Подробнее мы вернемся к этому после накопления соответ-

ствующего аппарата, а пока что необходимо сделать предупреждения.

Имеется один общий принцип, общезначимость которого не вызы-

вает сомнений: принцип свертки.

∃X

(π1,...,πn→t)

∀x

π1

, . . . , x

πn

(X(x

, . . . , x

) ⇔ A(x

, . . . , x

)) ,

где A — произвольная формула, не содержащая X свободно

Опираясь на принцип свертки, можно обосновывать многие полез-

ные свойства понятий высших порядков. Например, устанавливается

существование булевых операций над предикатами любых типов. Ниже

рассмотрена формула, выражающая существование объединения мно-

жеств объектов. Здесь мы иллюстрируем еще один часто применяемый

способ различения переменных разных типов: переменные для преди-

катов изображаются большими буквами, а их местность — скобками с

соответствующим числом аргументных мест. Таким образом, все боль-

шие буквы здесь типа o ∈ t, где o — тип объектов.

∀P (), Q() ∃R() ∀x(P (x) ∨ Q(x) ⇔ R(x)). (8.1)

Подытожим

Общее свойство логик — отсутствие конкретных понятий.

Формально оно выражается правилом подстановки.

Для языка высших порядков семантика определяется уже не

столь однозначно.

Данное маленькое ограничение, не сковывая свободы, избавляет от громадной опас-

ности произвольных рекурсивных определений, в частности, без него мы могли бы

определить предикат, эквивалентный собственному отрицанию.

212

ГЛАВА 8. СЕМАНТИКА КЛАССИЧЕСКОЙ ЛОГИКИ

Под логикой высших порядков традиционно понимают ти-

пизированный язык с принципом свертки.

Упражнения к § 8.5

8.5.1. Студент Гениалькис заявил, что никакие предикаторы не нужны,

поскольку у нас есть квантор свертки, и лучше подставлять просто

множества. Можете ли Вы ему возразить?

Глава 9. Семантические таблицы

для классической логики

§ 9.1. ОТ ТАБЛИЦ ИСТИННОСТИ

К СЕМАНТИЧЕСКИМ ТАБЛИЦАМ

Рассмотрим построение таблицы истинности пропозициональной фор-

мулы (A ⇒ B ∨ C) ⇒ (A ⇒ B) (см. табл. 9.1). Анализируя таблицу,

можно отметить, что большинство информации в ней избыточно. Та-

блицу можно значительно сократить, пользуясь следующими правила-

ми: для истинности дизъюнкции достаточно истинности одного из чле-

нов; для ложности конъюнкции достаточна ложность одного из членов;

истина следует из всего что угодно; из лжи следует все что угодно. Со-

кращенная таблица истинности показана на табл. 9.2.

При таком сокращении самым тонким местом является проверка то-

го, что ни один случай не упущен. Можно создавать много способов

сокращения таблиц истинности, но в некотором смысле все это будет

A B C B ∨ C A ⇒ B ∨ C A ⇒ B Формула

1 1 1 1 1 1 1

1 1 0 1 1 1 1

1 0 1 1 1 0 0

1 0 0 0 0 0 1

0 1 1 1 1 1 1

0 1 0 1 1 1 1

0 0 1 1 1 1 1

0 0 0 0 1 1 1

Таблица 9.1: Полная таблица истинности

214

ГЛАВА 9. КЛАССИЧЕСКИЕ СТ

A B C B ∨ C A ⇒ B ∨ C A ⇒ B Формула

0 — — — 1 1 1

1 1 — 1 1 1 1

1 0 0 0 0 0 1

1 0 1 1 1 0 0

Таблица 9.2: Сокращенная таблица истинности

изобретением велосипеда, поскольку, базируясь на правилах сокраще-

ния, голландский логик Бет (E. W. Beth) создал в 50-х годах формализм,

гарантирующий полноту разбора и выполняющий все прямые сокраще-

ния. Он основан на необходимых и достаточных условиях истинности

и ложности формул. Начнем с примера для той же формулы.

Ищем все возможные случаи, когда формула ложна.Если таковых не

найдется, то она истинна. Наша формула представляет собой имплика-

цию, импликация ложна, если ее посылка истинна, а заключение ложно.

Получаем следующее преобразование:

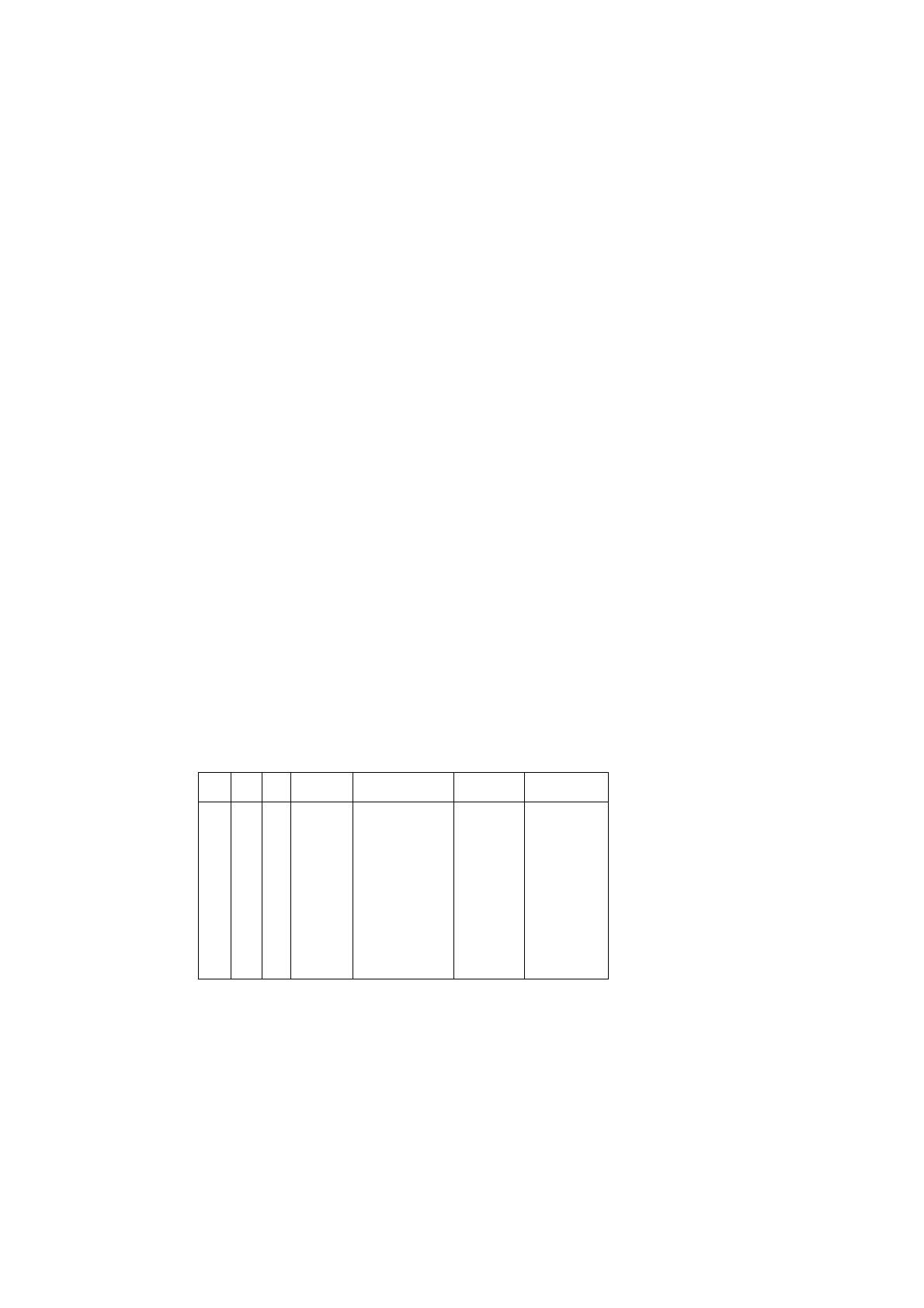
=| (A ⇒ B ∨ C) ⇒ (A ⇒ B)

|= A ⇒ B ∨ C

=| (A ⇒ B)

(9.1)

После применения аналогичного преобразования к третьей формуле по-

лучаем

=| (A ⇒ B ∨ C) ⇒ (A ⇒ B)

|= A ⇒ B ∨ C

=| (A ⇒ B)

|= A

=| B

(9.2)

Теперь приходится рассматривать условия истинности импликации.

Бет оптимально подобрал два случая, исчерпывающих все возможно-

сти,когда импликация истинна:необходимо и достаточно, чтобы

было

ложно либо

истинно. То, что мы разбираем два независимых случая,

отражается разбиением таблицы на подтаблицы, в которых общее лишь

то,что было получено до разделения. После разбиения импликации ана-

9.2. ПРАВИЛА РАЗБИЕНИЯ

215

логично разобьется и дизъюнкция.

=| (A ⇒ B ∨ C) ⇒ (A ⇒ B)

|= A ⇒ B ∨ C

=| (A ⇒ B)

|= A

=| B

=| A |= B ∨ C

B |= C

(9.3)

Здесь в двух из трех образовавшихся подтаблиц встретились проти-

воречия; такие подтаблицы называются закрытыми и отмечаются двой-

ной чертой. Оставшаяся подтаблица выдала тот единственный набор

значений, при котором формула ложна:

A истинно, B ложно и C истин-

но. Итак, мы получаем следующий метод проверки истинности форму-

лы либо построения контрпримера. Предполагаем, что формула ложна.

Строим семантическую таблицу и, если все ее подтаблицы закрылись,

приводим предположение о ложности формулы к абсурду и делаем вы-

вод, что она истинна. Иначе незакрытая подтаблица дает контрпример.

§ 9.2. ПРАВИЛА РАЗБИЕНИЯ ФОРМУЛ

В СЕМАНТИЧЕСКИХ ТАБЛИЦАХ

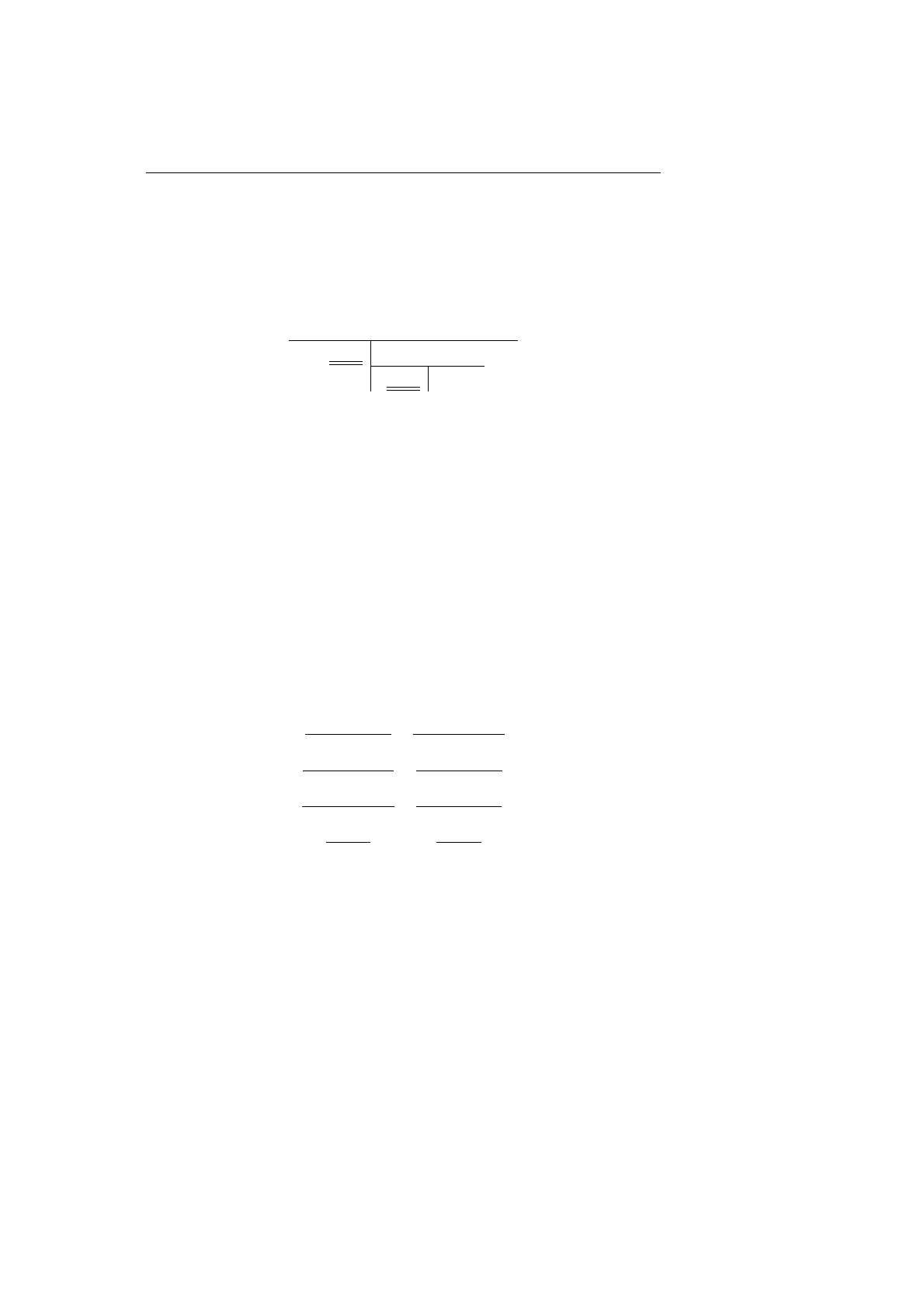
Просуммируем правила разбиения для связок логики высказываний.

|= A&B

|= A |= B

=| A&B

=| A | =| B

|= A ∨

|= A | |= B

=| A ∨ B

=| A =| B

|= A ⇒

=| A | |= B

=| A ⇒ B

|= A =| B

|= ¬A

=| A

=| ¬A

|= A

Если в правиле нижняя часть не разделена, результирующие форму-

лы остаются в той же подтаблице, в противном случае они распределя-

ются по двум новым подтаблицам, которые далее развиваются незави-

симо. Значит, подтаблицы семантической таблицы образуют бинарное

дерево.

Теперь остается заняться практикой и не забывать, что в любом до-

казательстве правильная общая структура значит не меньше, чем пра-

216

ГЛАВА 9. КЛАССИЧЕСКИЕ СТ

вильность отдельных шагов. Хорошо и то, что любая последователь-

ность правильных шагов приводит к результату, хотя, конечно, удачный

выбор порядка разбиений может сильно сократить таблицу.

Упражнения к § 9.2

9.2.1. Мы научились проверять на семантических таблицах высказыва-

ния на тождественную истинность. А как их проверять на тожде-

ственную ложность? Что в этом случае даст незакрытая семанти-

ческая таблица?

Проверить на семантических таблицах высказывания и рассужде-

ния.

9.2.2.

(A ⇒ B ∨ C) ⇒ (A ⇒ B) ∨ (A ⇒ C)

9.2.3.

(A ⇒ B) ∨ (A ⇒ C) ⇒ (A ⇒ B ∨ C)

9.2.4. (A&B ⇒ C) ⇒ (A ⇒ C) ∨ (B ⇒ C)

9.2.5. (A ⇒ C) ∨ (B ⇒ C) ⇒ (A&B ⇒ C)

9.2.6. (A&(B ∨ C)) ⇒ (A&C) ∨ (B&C)

9.2.7. (A&(B ∨ C)) ⇒ (A&C) ∨ (A&B)

9.2.8. (A&B) ∨ (A&C) ⇒ (A&(B ∨ C))

9.2.9. ((A ⇒ B) ⇒ (C ⇒ D)) ⇒ (A ⇒ C)&(D ⇒ B)

9.2.10. ((A ⇒ B) ⇒ C) ⇒ A ∨ (B ⇒ C)

9.2.11. A ∨ (B ⇒ C) ⇒ ((A ⇒ B) ⇒ C)

9.2.12. (A ∨ (B&C)) ⇒ (A ∨ B)&(A ∨ C)

9.2.13. (A ∨ B)&(A ∨ C) ⇒ (A ∨ (B&C))

9.2.14. (¬A ∨ B)&(A ∨ C) ⇒ B ∨ C

9.2.15. B ∨ C ⇒ (¬A ∨ B)&(A ∨ C)

9.2.16. (A ⇒ B)&(A ⇒ C)&(A ⇒ D) ⇒ ¬A

9.2.17. (B ⇒ A)&(C ⇒ A)&(D ⇒ A) ⇒ A

9.2. ПРАВИЛА РАЗБИЕНИЯ

217

9.2.18. (A ⇒ B ∨ C)&(B ⇒ ¬A)&(C ⇒ D)&(D ⇒ B) ⇒ (A ⇒ E)

9.2.19. (A&D ⇒ B ∨ C) ⇒ (A ⇒ B) ∨ (A ⇒ C) ∨ (D ⇒ B)

9.2.20. (A ⇒ B ∨ C)&(¬A ⇒ C) ⇒ B ∨ C

9.2.21. ((A ⇒ C) ⇒ D)&¬D ⇒ A&¬C

9.2.22. (A ⇒ B)&(B ⇒ C) ⇒ (¬A ⇒ C)

9.2.23. Майор Тронин в результате расследования установил, что два

сотрудника организации п/я № 13являются агентами.Медников —

агент английский либо американский, а Иванов — английский ли-

бо израильский. С присущей ему проницательностью тов. Тронин

сделал вывод, что п/я № 13 находится под контролем “Intelligence

Service”. Прав ли он?

9.2.24. Если в России пытаются проводить реформы,то начинается смут-

ное время. Если начинается смутное время,то либо наступает гра-

жданская война, либо иностранное нашествие, либо Россия теря-

ет часть территорий. Если наступает гражданская война, то насе-

ление испытывает ужасные бедствия. Не лучше приходится на-

селению и при нашествии. Сейчас в России пытаются проводить

реформы. Значит, российский народ ждут ужасные бедствия.

9.2.25.

(L. Carroll*)

Он никогда не поет больше часа. Если кто-то поет

больше часа, он надоедает окружающим. Тот, кто не надоедает

окружающим, — желанный гость. Значит, он — желанный гость.

9.2.26. Создайте правила разбиения для эквивалентности и на их осно-

ве постройте семантическую таблицу для

((A ⇔ B) ⇔ C) ⇔

(A ⇔ (B ⇔ C)).

9.2.27.

(J. Venn)

Существовал клуб с такими правилами:

1. Члены финансового комитета должны избираться среди чле-

нов общей дирекции.

2. Нельзя быть одновременно членом общей дирекции и чле-

ном библиотечного комитета, не будучи членом финансового

комитета.

3. Ни один член библиотечного совета не может быть членом

финансового комитета.

218

ГЛАВА 9. КЛАССИЧЕСКИЕ СТ

Упростите правила.

§ 9.3. СЕМАНТИЧЕСКИЕ ТАБЛИЦЫ С КВАНТОРАМИ

В отличие от таблиц истинности, метод семантических таблиц обобща-

ется на всю логику предикатов. Здесь техническое улучшение, которым

казалось исключение лишних случаев из перебора, переходит в прин-

ципиальное. Это — типичная ситуация в истории науки. Стремление

улучшить изложение какого-то темного места гораздо чаще приводит к

принципиальным открытиям, чем амбициозные попытки перевернуть

науку и создать какую-либо “общую теорию всего”. Теория относитель-

ности была создана Эйнштейном в результате доводки до логического

конца анализа электродинамики движущихся тел, общая теория отно-

сительности также почти как техническое улучшение интенсивно вед-

шихся в то время многими крупными учеными работ по применению

тензорных методов к механике. А вот все его многолетние усилия со-

здать общую теорию поля не привели ни к чему. Лобачевский создал

неевклидову геометрию, пытаясь усовершенствовать изложение геоме-

трии для исключительно тупого контингента слушателей, примерно со-

ответствующего нынешнему факультету повышения квалификации

Рассмотрим условия истинности и ложности всеобщности и суще-

ствования. Поскольку ∀x A истинна тогда и только тогда, когда A(c)

истинно для любого конкретного c, мы, имея |= ∀x A, можем полу-

чить A(c

) всякий раз, когда в таблице либо подтаблице появляется объ-

ект c

.Если же =| ∀x A, то мы знаем лишь, что существует такой объ-

ект a, для которого A(a) ложно. Чтобы отобразить это, постулируем

=| A(c

n+1

) для нового,ранее в таблице не встречавшегося, объекта c

n+1

(называемого вспомогательной константой).Таким образом,приходим

к следующим правилам разбиения для кванторов.

|= ∀x A

|= A(c

)

=| ∀x A

=| A(c

n+1

)

|= ∃x A

|= A(c

n+1

)

=| ∃x A

=| A(c

)

(9.4)

Известно, что нет ничего легче, как не задумываясь ответить на вопрос. Один дурак,

при наличии эрудиции либо уверенности в себе, может ответить на столько вопросов,

что сто умных не смогут задать.

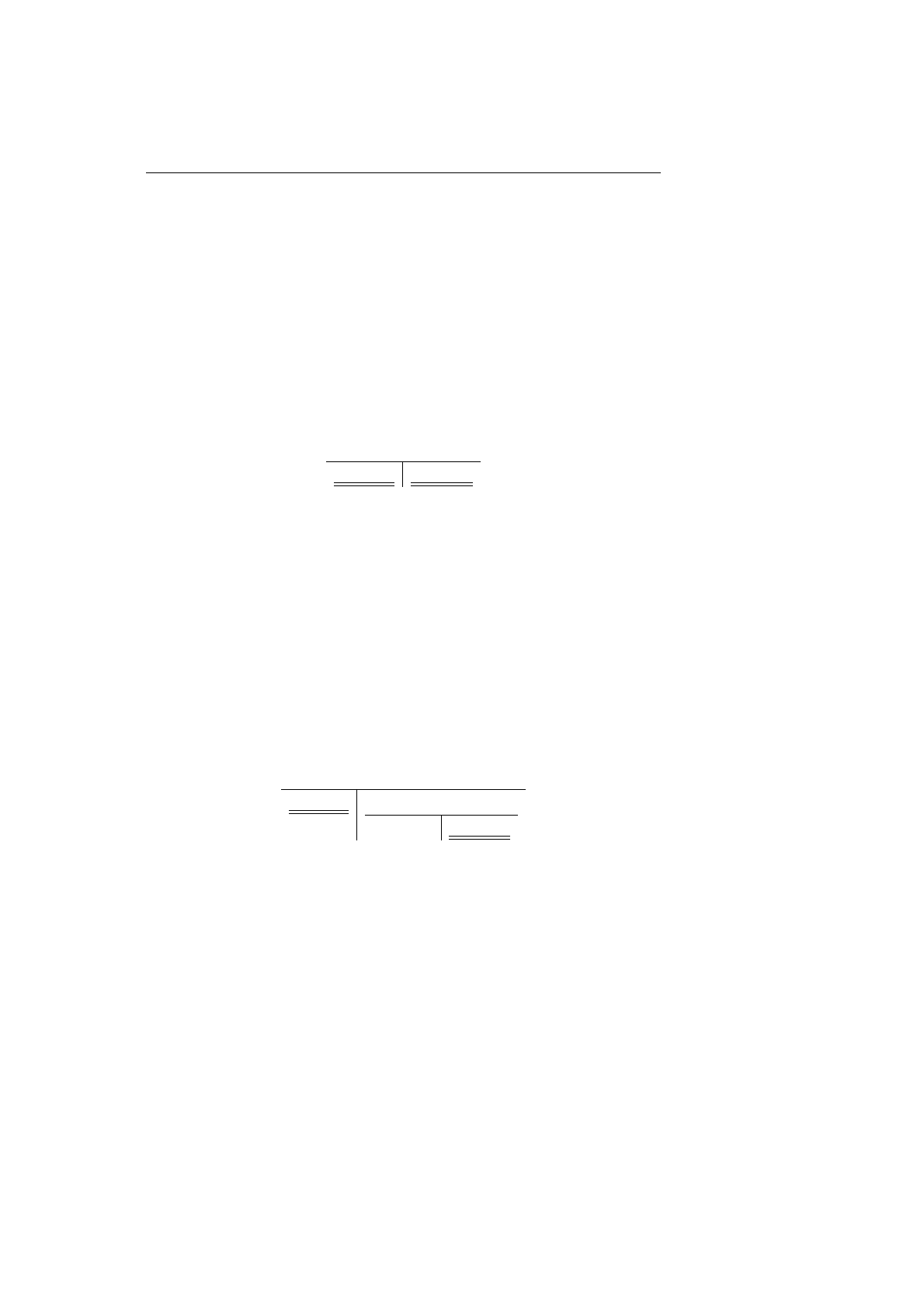
9.3. СЕМАНТИЧЕСКИЕ ТАБЛИЦЫ С КВАНТОРАМИ

219

Рассмотрим пример: проверка формулы

∃x A(x)&∀x B(x) ⇒ ∃x (A(x)&B(x)).

=| ∃x A(x)&∀x B(x) ⇒ ∃x (A(x)&B(x))

|= ∃x A(x)&∀x B(x)

=| ∃x (A(x)&B(x))

|= ∃x A(x)

|= A(c

)

|= ∀x B(x)

|= B(c

)

=| (A(c

)&B(c

))

=| A(c

) =| B(c

)

(9.5)

В дальнейшем для единообразия вспомогательные константы обо-

значаются

, c

, ... Мы ввели объект c

, рассмотрев |= ∃x A(x), по-

сле чего подставили его в две другие кванторные формулы. Следующий

пример показывает, что не всегда удается обойтись одним объектом.

=| ∀x (A(x) ∨ B(x)) ⇒ ∀x A(x) ∨ ∀x B(x)

=| ∀x A(x) ∨ ∀x B(x)

|= ∀x (A(x) ∨ B(x))

=| ∀x A(x)

=| A(c

)

=| ∀x B(x)

=| B(c

)

|= A(c

) ∨ B(c

)

|= A(c

) ∨ B(c

)

|= A(c

) |= B(c

)

|= A(c

) |= B(c

)

(9.6)

Здесь видно, что нам пришлось использовать

|= ∀x (A(x) ∨ B(x))

дважды: для c

и c

. И именно из-за различия этих двух значений табли-

ца не закрылась; незапертая подтаблица дает следующую опровергаю-

щую модель:

A 0 1

B 1 0

220

ГЛАВА 9. КЛАССИЧЕСКИЕ СТ

Следующий пример иллюстрирует еще две особенности, возникаю-

щие в предикатных семантических таблицах: возможность бесконечно-

го порождения констант и аномалия с первым объектом. Он заодно по-

казывает, что незапертость подтаблицы приходится порою усматривать

более или менее косвенно, а не устанавливать доведением построения

до конца, и что одна и та же формула может использоваться бесконечное

количество раз.

=| ∀x ∃y A(x, y) ⇒ ∃x A(x, x)

=| ∃x A(x, x)

|= ∀x ∃y A(x, y)

|= ∃y A(c

, y)

|= A(c

, c

)

=| A(c

, c

)

|= ∃y A(c

, y)

|= A(c

, c

)

=| A(c

, c

)

∙∙∙

(9.7)

Итак, бесконечно порождаются новые константы

,для которых вы-

полнено |= A(c

, c

i+1

),но =| A(c

, c

).Немного разобравшись с анализи-

руемой формулой, мы видим, что построенная опровергающая модель

отнюдь не минимальная. Достаточно было бы рассмотреть множество

из двух элементов.

Упражнения к § 9.3

Проверить на семантических таблицах высказывания и рассу-

ждения.

9.3.1.

[K]

Некоторые цыплята — кошки. Некоторые кошки знают фран-

цузский язык. Значит, некоторые цыплята знают французский.

9.3.2.

∃x (A(x) ⇒ ∀y A(y))

9.3.3.

∀x (A ∨ B(x)) ⇒ A ∨ ∀x B(x).

Р. Смальян прокомментировал это высказывание следующим анекдотом. Заходит

ковбой в бар и говорит бармену: “Мне налей и всем налей. Такой уж я человек: когда

я пью, все пьют”. Через некоторое время: “Мне повтори и всем повтори. Такой уж я

человек: когда я пью, все пьют”. Затем кладет на стойку деньги: “С меня возьми и со

всех возьми. Такой уж я человек: когда я плачу, и все платят”.