Непейвода Н.Н. Прикладная логика

Подождите немного. Документ загружается.

9.9. СЕЧЕНИЯ

261

Рассмотрим теперь кванторы.

Γ ⊕ {=| ∃x A(x), =| A(x | t), |= C}

Γ ⊕ {=| ∃x A(x), |= C}

Γ ⊕ {=| ∃x A(x), =| C}

Γ ⊕ {=| ∃x A(x)}

=⇒

Γ ⊕ {=|∃x A(x), =|A(x | t), |=C}

Γ ⊕ {=|∃x A(x), =|A(x | t), =|C}

Γ ⊕ {=| ∃x A(x), =| A(x | t)}

Γ ⊕ {=| ∃x A(x)}

Для вспомогательной константы:

Γ ⊕ {|= A(c

n+1

), |= C}

Γ ⊕ {|= ∃x A(x), |= C}

Γ ⊕ {|= ∃x A(x), =| C}

Γ ⊕ {|= ∃x A(x)}

=⇒

Γ ⊕ {|= A(c

n+1

), |= C}

Γ ⊕ {|= A(c

n+1

), =| C}

Γ ⊕ {|= A(c

n+1

)}

Γ ⊕ {|= ∃x A(x)}

, Σ

получаются обращениями соответствующих выводов.

Для квантора ∀ преобразования аналогичны.

Шаг 1. Если одна из посылок правила сечения является аксиомой,

то рассматриваем следующие два подслучая.

1. Формула сечения не участвует в противоречии. Тогда и в результа-

те правила сечения имеется то же противоречие и, следовательно,

результат является аксиомой.Значит,правило сечения вместе с его

посылками и всем, что лежит над ними, можно просто опустить.

2. Формула сечения участвует в противоречии.Здесь опять придется

разобрать два подслучая, но они совершенно симметричны.

(a) Пусть противоречием является левая посылка.Тогда она име-

ет вид

Γ ⊕ {=| A, |= A},

а правая, соответственно,

Γ ⊕ {=| A, =| A}.

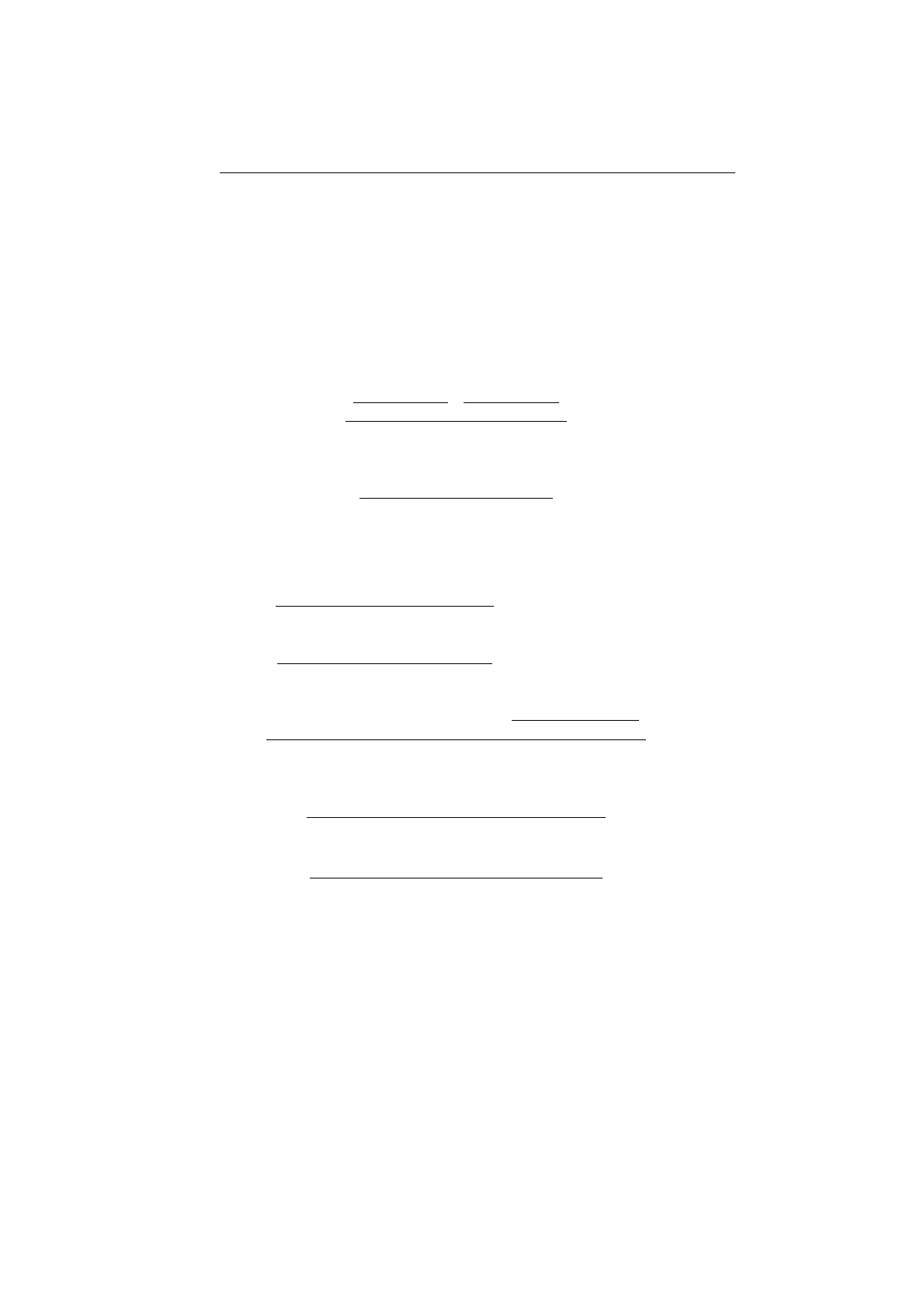
262

ГЛАВА 9. КЛАССИЧЕСКИЕ СТ

Заключение сечения имеет вид Γ⊕{=| A}. Значит,его можно

получить из правой посылки преобразованием сокращения

(предложение 9.9.4), не увеличивая длины вывода и сложно-

сти формул.

(b) Симметрично.

Связка

¬. Для отрицания

Γ ⊕ {=| A}

Γ ⊕ {|=

Γ ⊕ {|= A}

Γ ⊕ {=|

=⇒

Γ ⊕ {|= A} Γ ⊕ {=| A}

Связка ∀. Для кванторов

⊕ {|= A[x | t

], |= ∀x A(x)}

⊕ {|= ∀x A(x)}

⊕ {|= A[x | t

], |= ∀x A(x)}

⊕ {|= ∀x A(x)}

Σ Ψ

Γ ⊕ {|= ∀x A(x)}

Γ ⊕ {=| A(c

n+1

)}

Γ ⊕ {=| ∀x A(x)}

=⇒

[x | t]

⊕ {|= A[x | t

]} Γ

⊕ {=| A[x | t

]}

[x | t

]

⊕ {|= A[x | t

]} Γ

⊕ {=| A[x | t

]}

Здесь в выводе Σ выделены все применения правила |= ∀ к формуле се-

чения. Σ

— выводы посылок таких правил, в которых имеются другие

применения тех же правил,Σ

—выводы, в которых других применений

9.9. СЕЧЕНИЯ

263

|= ∀ к формуле сечения нет. Σ

получается из Σ

устранением послед-

него применения кванторного правила по предложению 9.9.5, а Σ

—

вычеркиванием всех формул |= ∀x A(x).

Связка

⇒. Пусть главная логическая связка формулы сечения —

импликация и в обоих посылках сечения она разбирается. Тогда имеем

следующее преобразование:

Γ ⊕ {=| A} Γ ⊕ {|= B}

Γ ⊕ {|= A ⇒ B}

Γ ⊕ {|= A, =| B}

Γ ⊕ {=| A ⇒ B}

=⇒

Γ ⊕ {=| A, |= B} Γ ⊕ {|= A, |= B}

Γ ⊕ {|= B}

Γ ⊕ {|= A, =| B} Γ ⊕ {=| A, =| B}

Γ ⊕ {=| B}

Выводы со штрихами — ослабления соответствующих исходных вы-

водов.

Связки

&, ∨. Для остальных бинарных пропозициональных связок

преобразование определяется аналогично.

Из всех шагов нормализации обоснования требуют лишь квантор-

ные. Достаточно заметить, что после устранения первых применений

кванторного правила последующие за ними также становятся первыми,

и т. п. Это легко оформляется индукцией.

Теорема 9.3. (Сильная теорема нормализации)Любая последователь-

ность шагов нормализации за конечное число шагов приводит к выводу

без сечений.

Доказательство. Для обоснования этого достаточно приписать любо-

му сечению высоту, которая будет уменьшаться на каждом шаге норма-

лизации и оценивается в единицах, множество которых удовлетворяет

свойству бесконечного спуска. Натуральными числами оценить не по-

лучается из-за того, что слишком часто при нормализации одно сечение

заменяется на несколько; приходится оценивать ординалами. А изобре-

тение такой оценки можно рассматривать как задачу на ‘отлично’ для

студента (подсказка: удобнее всего воспользоваться сложением по Ку-

ратовскому и возведением в степень

264

ГЛАВА 9. КЛАССИЧЕСКИЕ СТ

Упражнения к § 9.9

9.9.1. (Для тех, кто хорошо знает официальные правила шахмат и играл

в турнирах)Приведенное в примечании на стр.254доказательство

ошибочно. Найдите неточность и исправьте ее

9.9.2. В японских шахматах ничьей нет. Тот, кто сделал ход, ведущий к

троекратному повторению позиции, считается проигравшим. Ко-

ролю не запрещено ходить под шах, так что при возникновении

ситуации, которая в европейских шахматах считалась бы патом,

король обязан пойти под бой и пасть смертью храбрых

. В на-

чальной позиции многие фигуры

могут походить и затем вер-

нуться назад. Можно ли перенести наше доказательство на моди-

фицированные японские шахматы? А может быть,Вы придумаете

для них другое?

9.9.3. Если не отказываться от неэлементарных противоречий, какой из

пунктов доказательства теоремы об устранении сечений провали-

вается? Как можно было бы спасти его, изменив меру сложности

вывода?

9.9.4. Студент Гениалькис принес Вам доказательство того, что каждый

вывод секвенции

Γ ⊕ {=| ∃x A(x)} можно перестроить в вывод

секвенции Γ ⊕ {=| A(x | t

), . . . , =| A(x | t

)} для некоторых

, . . . , t

, не увеличивая число шагов в выводе, но Вы тетрадь с

доказательством потеряли. Как Вы ответите на вопрос Гениальки-

са, верно ли его доказательство?

Ошибка возникает лишь при взаимодействии с полной системой правил шахматной

игры в официальных соревнованиях.

На самом деле там такая ситуация может возникнуть лишь теоретически, поскольку

взятые фигуры (кроме, естественно, короля) переходят на сторону противника и воюют

против бывших своих. Но это уже не имеет отношения к математическому содержанию

задачи.

Правда, на сей раз кроме коня, поскольку пешки стоят в третьем ряду, а конь ходит

только вперед. Но это также не имеет отношения к задаче.

Поскольку студент гениальный, все доказательства верных теорем, которые он дает,

правильны, а поскольку человеку свойственно ошибаться ...

Глава 10. Элементы

нестандартного анализа

§ 10.1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ

История развития математических концепций является одним из при-

меров творческого развития. В ней выполнены многие общие законо-

мерности такого развития. Стоит напомнить некоторые из них, которые

необходимо знать любому, решающему сложные нестандартные прак-

тические задачи

1. Ни одно принципиально новое открытие не может быть обосно-

вано его творцами строго. Более того, предложенные ими обосно-

вания, как правило, содержат серьезные ошибки и впоследствии

опровергаются.

2. Тот, кто боится делать предположения, противоречащие общепри-

нятому и даже “здравому смыслу”, не может открыть ничего но-

вого

Решение т. н. сложных нестандартных математических задач принципиально отли-

чается. Здесь основным интересом является спортивный: решить поставленную авто-

ритетным человеком задачу раньше других и получить славу и награду. Естественно,

как и в спорте, имеются судейские коллегии, проверяющие чистоту достижения, т. е.

прежде всего его соответствие принятым правилам и традициям. Реального творчества

здесь обычно не так уж много, и чаще всего творческие достижения принадлежат не

тем, кто в конце концов решил задачу. Примерами здесь являются 10-я проблема Гиль-

берта и теорема Ферма.

В теории творческого мышления это называется “инертностью”. В психологии это

называется “рутинностью мышления”.

266

ГЛАВА 10. НЕСТАНДАРТНЫЙ АНАЛИЗ

Тот, кто увлекается своими предположениями и начинает выда-

вать их за истины, после этого также не может выдать ничего но-

вого

3. Не только логика открытия и обоснования, но и логика нахожде-

ния обоснования и его изложения принципиально различаются.

4. При каждом строгом обосновании мы в значительной степени те-

ряем из виду исходную задачу и, более того, порою искажаем ее

до неузнаваемости.

Интереснейшим и показательным примером творческого развития в

математике является создание математического анализа.Известно,что в

нынешнее время анализ излагается в учебниках совсем не так, как изла-

гали его создатели, да и другие ученые вплоть до конца XVIII в. Основ-

ными понятиями служат множество,предел, функция, определяемая че-

рез множества, последовательность, определяемая через функцию.Что

такое множество и зачем оно нужно в математике, осознано было лишь

во второй половине XIX века

, поэтому множеств создатели анализа не

знали, а вот все остальные понятия были центральными и для них. Но

воспринимались они совсем не так, как в современной математике.

Так, например, практически никто не замечал аналогий между по-

нятиями последовательности и функции. Если с последовательностью

связывалась в основном идея бесконечно продолжающегося порожде-

ния элементов, возможно, путем свободного выбора, то насчет функции

практически не было сомнений, что это — либо аналитическое выраже-

ние,задающее связь аргумента с результатом, либо непрерывная кривая,

которая может быть начерчена, либо какой-то другой тип их явно задан-

ной взаимосвязи. Поэтому и появился термин “неявная функция”, озна-

чавший функцию,для вычисления которой требовалось решить уравне-

ние, зависящее от ее аргумента как от параметра.

К такому пониманию функции в некотором смысле вернулись в со-

временной теории вычислимости, но там первичны именно законы, по-

В психологии это называется “переходом ценных идей в сверхценные”.

Хотя в традиционной логике давно уже использовалось понятие класса,соответству-

ющее по содержанию понятию множества, и попытки построить исчисление классов

начались практически одновременно с созданием математического анализа; в частно-

сти, к ним приложили руку Лейбниц, Эйлер, Больцано...

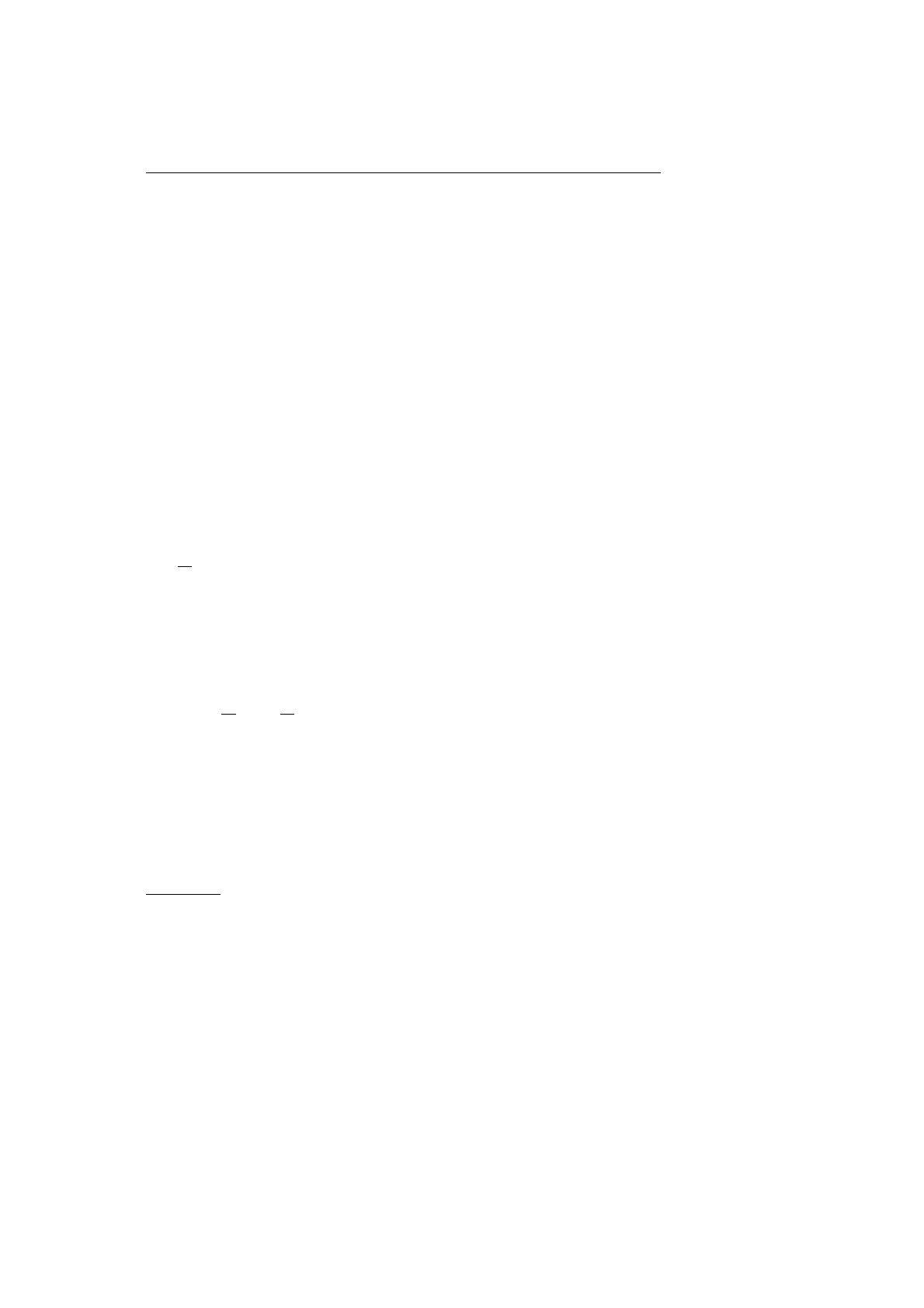
10.1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ

267

рождающие последовательности, а законы, порождающие функции дей-

ствительного переменного, косвенно определяются через них.

Но более всего бросаются в глаза расхождения в определении пре-

дела и наличие в математике конца XVII–XVIII в. понятий актуально

бесконечно малых величин. Математический анализ даже назывался в

то время анализом бесконечно малых. Актуальные бесконечности были

полностью отброшены при канонизации и уточнении изложения анали-

за в первой половине XIX в. Еще в 1960 г. считалось, что они забыты

навсегда и представляют интерес лишь для историков науки и издате-

лей трудов классиков того времени. Но радикальное изменение взгляда

на математику, порожденное математической логикой, привело к их не-

ожиданному возрождению на абсолютно строгом уровне

Важнейшими из, казалось бы, навсегда отвергнутых понятий были

понятия бесконечно малых и бесконечно больших величин и понятие

дифференциала функции (которое Ньютоном и Лейбницем считалось

первичным по отношению к понятию производной).

dy было прираще-

нием функции y = f(x) при бесконечно малом изменении x. Отноше-

ние

было действительно результатом деления dy на dx. Конечно же,

при делении одного бесконечно малого числа на другое могло получить-

ся конечное число, но тонкость в том, что это конечное число могло со-

держать и бесконечно малую компоненту, которая считалась пренебре-

жимой по сравнению с конечным результатом и отбрасывалась.

Рассмотрим, например, как первоначально доказывалась теорема о

производной произведения двух функций.

Пусть

= a,

= b. Пусть u = y ∙ z. Тогда при бесконечно малом

приращении dx аргумента x имеем:

u = (y + dy) ∙ (z + dz) = yz + z dy + y dz + dy ∙ dz.

Отбрасывая пренебрежимо малую величину dy ∙ dz, получаем

du = y dz + z dy.

Тем не менее некоторые из понятий анализа бесконечно малых, и очень полезные,

до сих пор не нашли новой интерпретации. Да к ним добавились еще другие понятия,

созданные гениальным английским математиком-прикладником рубежа XIX–XX веков

У. Хевисайдом. Лишь простейшие из них получили интерпретацию в теории обобщен-

ных функций, но, кажется, традиционными аналитическими средствами здесь далеко

не продвинешься.

268

ГЛАВА 10. НЕСТАНДАРТНЫЙ АНАЛИЗ

На этом выводе многие математики прекращали изложение, поскольку

именно дифференциал, а не производная, считался первичным поняти-

ем. Но некоторые (как правило, самого высокого класса либо с наиболее

тонким чувством математической строгости) делали еще пару шагов.

z dy + y dz + dy ∙

= z

+ y

dy ∙

Последний член получившегося выражения бесконечно мал, поэтому

отбросим его и получим

= z

+ y

Предел также интенсивно рассматривался математиками того вре-

мени, но определялся весьма расплывчато: как “первое и последнее”

значение выражения, соответственно, при приближении к точке a и при

удалении от нее. Интеграл определялся как сумма бесконечно большого

числа бесконечно малых величин, примерно как

i=(b−a)/ε

i=0

f(x + iε) ε.

Впрочем, такое выражение считалось бы неприличным, поскольку уж о

бесконечно больших натуральных числах математики, ясное дело, сты-

дились говорить

Подобные фокусы,когда бесконечно малые величины то полноправ-

но использовались в преобразованиях, то вдруг отбрасывались, причем

иногда не полностью, а частично, а ответ, тем не менее, выходил пра-

вильный,использовались некоторыми благонамеренными образованны-

ми людьми, в частности, епископом Беркли, для доказательства суще-

ствования Бога, что, как и всякая благоглупость, лишь компрометиро-

вало и ту цель, ради которой это делалось, и те средства, которые при

Хотя поскольку аксиома Архимеда, говорящая,что для любых двух x, y > 0 найдется

такое

n, что

x + ∙ ∙ ∙ x

| {z }

раз

> y,

уже была осознана в то время, казалось бы, очевидно, что,сказав A, необходимо сказать

B: принять существование бесконечно больших натуральных чисел. Но в жизни (и

в науке тоже) нежелательные следствия, сколь бы очевидны они ни были, почему-то

очень долго не замечаются.

10.1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ

269

этом использовались. Естественно, что критически мыслящие матема-

тики в конце концов больше не захотели “приносить строгость в жертву

успеху”, и в начале XIX в. началось движение за изгнание бесконеч-

но малых и замену их т. н. “ε − δ формулировками”, которыми мучают

нынешних студентов на I курсе

. Эта реформация часто связывается с

именем французского математика Коши, который, как выяснилось в ре-

зультате анализа его работ, на самом деле использовал старые и новые

методы вперемежку, но, правда, не стеснялся передоказывать новыми

методами утверждения, ранее доказанные им старыми способами.

К середине XIX в. стало неприличным пользоваться актуально бес-

конечно большими и бесконечно малыми величинами, уровень строго-

сти математических доказательств поднялся настолько, что превзошел

достигнутый в древнегреческой геометрии и спровоцировал появление

столь неприятной для традиционного математического мировоззрения

науки, как математическая логика.

Первые же результаты математической логики привели к выводу,что

в строгих математических рассмотрениях большинство понятий не мо-

гут иметь прямой интерпретации. Они являются идеальными понятия-

ми (в отличие от реальных, взятых из практики). От идеальных понятий

в принципе можно было бы избавиться

, таким образом, они необяза-

тельны и служат, с плоской прикладной точки зрения, лишь для сокра-

щения выкладок.

Идеальным является уже понятие действительного числа, посколь-

ку оно предполагает бесконечную последовательность уточняющихся

приближений

. А что уж там говорить о понятиях непрерывной функ-

ции и т. п.

Уже на данном примере видно, что идеальность бывает разной сте-

пени, и введя идеальные понятия, мы часто вынуждены вводить еще

И правильно мучают! Если Вы ими не овладели, Вам нечего и читать эту гла-

ву дальше.

Данное выражение означает, что выкладки и рассуждения, включающие идеальные

понятия, но приводящие к реальному результату, можно было бы перестроить таким

образом, чтобы изгнать из них все идеальные понятия. Но насколько при этом услож-

нятся преобразования и доказательства, в расчет не принимается.

Если копнуть поглубже, то возникают сомнения в реальности и рациональных, и

натуральных чисел, поскольку мы не учитываем при их определении реальной конеч-

ности наших ресурсов и нашего времени; но эта степень идеальности, безусловно, на-

много ниже.

270

ГЛАВА 10. НЕСТАНДАРТНЫЙ АНАЛИЗ

более идеальные, чтобы успешно работать с уже имеющимися. Далее

чувствуется, что плоская

прикладная точка зрения в чем-то ущербна,

поскольку основные математические результаты, оказывается, касают-

ся именно идеальных понятий.

Идеальные понятия после их осознания стали полноправным пред-

метом изучения и в философии, и в теории творческого мышления, и в

психологии. Выяснились весьма любопытные факты, которые обосно-

вываются, в частности, и методами математической логики.

Потеря эффективности мышления при отказе от идеальных поня-

тий столь грандиозна, что человек оказывается отброшенным на уро-

вень разрозненных эмпирических рецептов и не может создать ничего

существенно нового. Более того, идеальные понятия дают возможность

выразить множество эмпирических рецептов одним общим утвержде-

нием, и порою оно оказывается столь выразительно (например, прин-

цип неподвижной точки: любое непрерывное отображение

n-мерного

круга в себя имеет неподвижную точку), что унифицируемые им реце-

пты выглядят совершенно по-разному и уж конечно относятся к разным

областям знания.

Поэтому неудивительно, что среди ученых, занимающихся точными

науками, популярна точка зрения Платона: на самом деле именно иде-

альные понятия первичны, а так называемые “реальные” служат лишь

их несовершенными и бледными отражениями, их тенями. Если хоро-

шенько вдуматься, то поймешь, что этот взгляд достаточно обоснован: в

частности, одно из самых “реальных и материальных” понятий, по сути

дела породившее весь мировоззренческий материализм, — деньги —

на самом деле ирреально, оно является лишь результатом соглашения

между людьми, что доказали события в Камбодже, когда захватившие

власть ультракоммунисты отменили деньги и никто не поднимал даже

доллары. Удивительная эффективность и красота идеальных понятий

и неэффективность и безобразие ползучего, эмпирического мышления

просто провоцируют этот взгляд

Подчеркиваю, плоская! Плоская теоретическая точка зрения на самом деле столь же

ущербна.

Сам автор весьма близок к данному взгляду, но не считает возможным навязывать его

как единственно правильный. Любая человеческая интерпретация односторонняя и не-

полная. Поэтому всегда нужно наряду со своим взглядом признавать и альтернативный

ему, а именно: что идеальные понятия суть лишь имена, получаемые путем последова-

тельных обобщений опыта, и зачастую эти обобщения поднимаются столь высоко, что