Неумывакин Ю.К., Смирнов А.С. Практикум по геодезии

Подождите немного. Документ загружается.

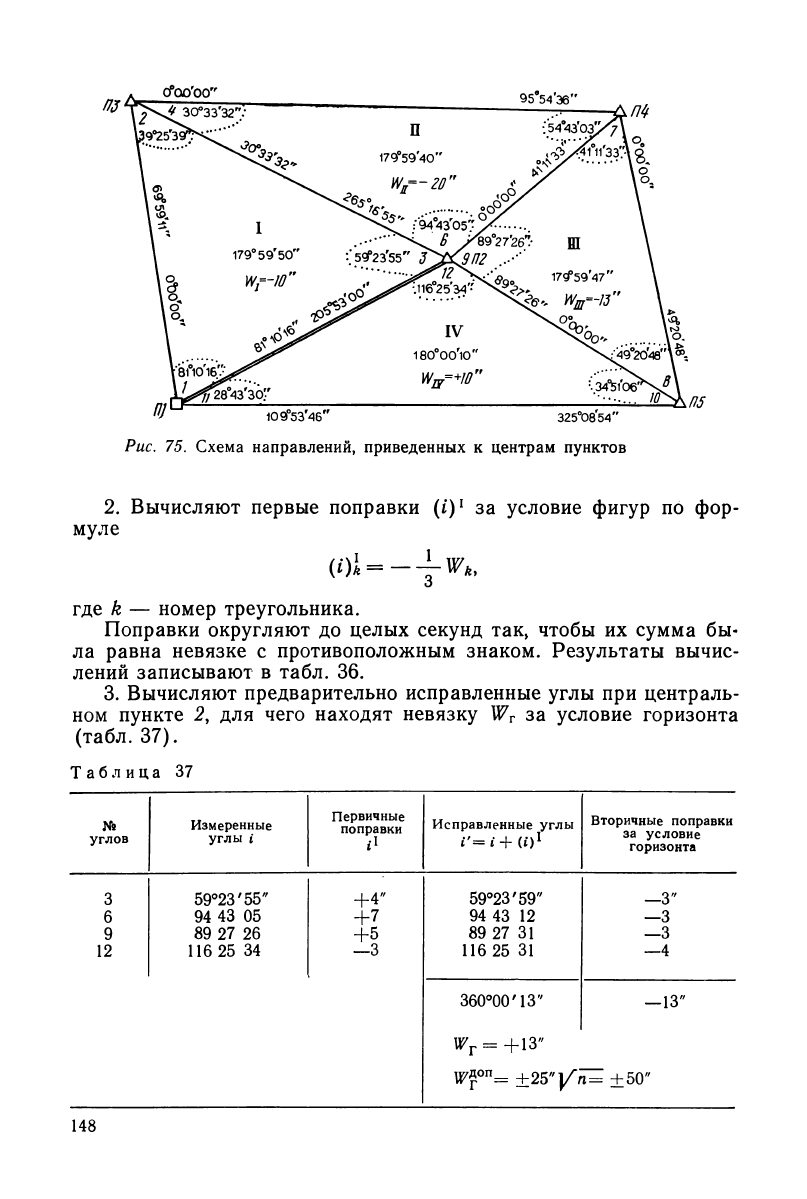
Рис. 75. Схема направлений, приведенных к центрам пунктов

2. Вычисляют первые поправки (i)

за условие фигур по фор-

муле

(Oi—

где k — номер треугольника.

Поправки округляют до целых секунд так, чтобы их сумма бы-

ла равна невязке с противоположным знаком. Результаты вычис-

лений записывают в табл. 36.

3. Вычисляют предварительно исправленные углы при централь-

ном пункте 2, для чего находят невязку W

за условие горизонта

(табл. 37).

Таблица 37

№

углов

Измеренные

углы i

Первичные

поправки

Исправленные углы

r=f+(i)

Вторичные поправки

за условие

горизонта

59°23'55"

94 43 05

89 27 26

116 25 34

+4"

—3

59°23'59"

94 43 12

89 27 31

116 25 31

1 1 1

4*.

СО

360°00'13"

—13"

= +13"

= ±25"y

n= ±50"

№

углов

Первично

исправленные

углы

Синусы

углов

= ctg Afr

№

углов

Первично

исправленные

углы

Синусы

углов

= ctg B

Вторичные

поправки

)" =

-(B

)»

8Г10'20"

0,988154

+0,16

39°25'44" 0,635120

+ 1,22

+ 1,38

—3,3"

30 33 40

0,508457

+ 1,69 5

54 43 И

0,816336

+0,71

+2,40

-5,7

41 И 38

0,658609

+ 1,14

49 20 54

0,758684

+0,86

+2,00

—4,7

10 34 51 04

0,571446

+ 1,44

28 43 29

0,480602

+0,82 +3,26

—7,7

СО

0,189096

0,189048

п=(-^-

)

+52,6

(Ча„ + О

22,29;

k ' Bk'

2 (?! + <&) = 12,3.

Г«°

2,5m

/2 (q\

+ = ± 25" /12,3 = ± 88";

+52,6"

+ ~

22,3

= -

2,36";

Ш" = - (В>;= /С (q

. + q

Контроль:

2 (ЯА

+ Ч

Вк

) (Ak)" =-W

= - 52,8"

«-(+52,6").

Пункты

Исходные

№

2 з

4 5 1

Обозначения

Определяемые

исх

64°01'16" 244

01'16"

123

25'12"

272°51'38"

356°56'48" 92

44'53"

гол

(fc)

—

+59 23 56 —30 33 34

—95 54 50

—84 И 55

—28 43 37

64 01 16

303 25 12

92 51 38

176 56 48 272 44 53 64 01 16

X, м

+4910,43

+6499,13

+6323,39

+3959,01

+4098,31

+4098,30

+4910,43

+6499,13

+6323,39

+3959,01

ДХ

+812,13

1588,70

—175,74

—2364,38

139,30

cos а

+0,438040

+0,550772

—0,049905

—0,998580

+0,047944

S, м

1854,01

2884,50

3521,41

2367,74 2905,55

sin a

+0,898956

—0,834656

+0,998754

+0,053266

—0,998850

АУ

+1666,67

—2407,57

+3517,02

126,12

-2902,21

^исх

0,00

1666,67

-740,90 +2776,12

+2902,24

12 К, м

+1666,67

—740,90 +2776,12

+2902,24 +0,03

4. Вычисляют вторые поправки в каждый из связующих углов

треугольника в размере половины поправки за условие горизонта в

центральный угол с противоположным знаком. Например, для вто-

рого треугольника вторые поправки в углы 5 и 4 будут равны:

(5)» = ((4)" = --^(6)" = + 1,5"

и т. д.

5. Находят первичную поправку по формуле

(О' = (О

+ (О

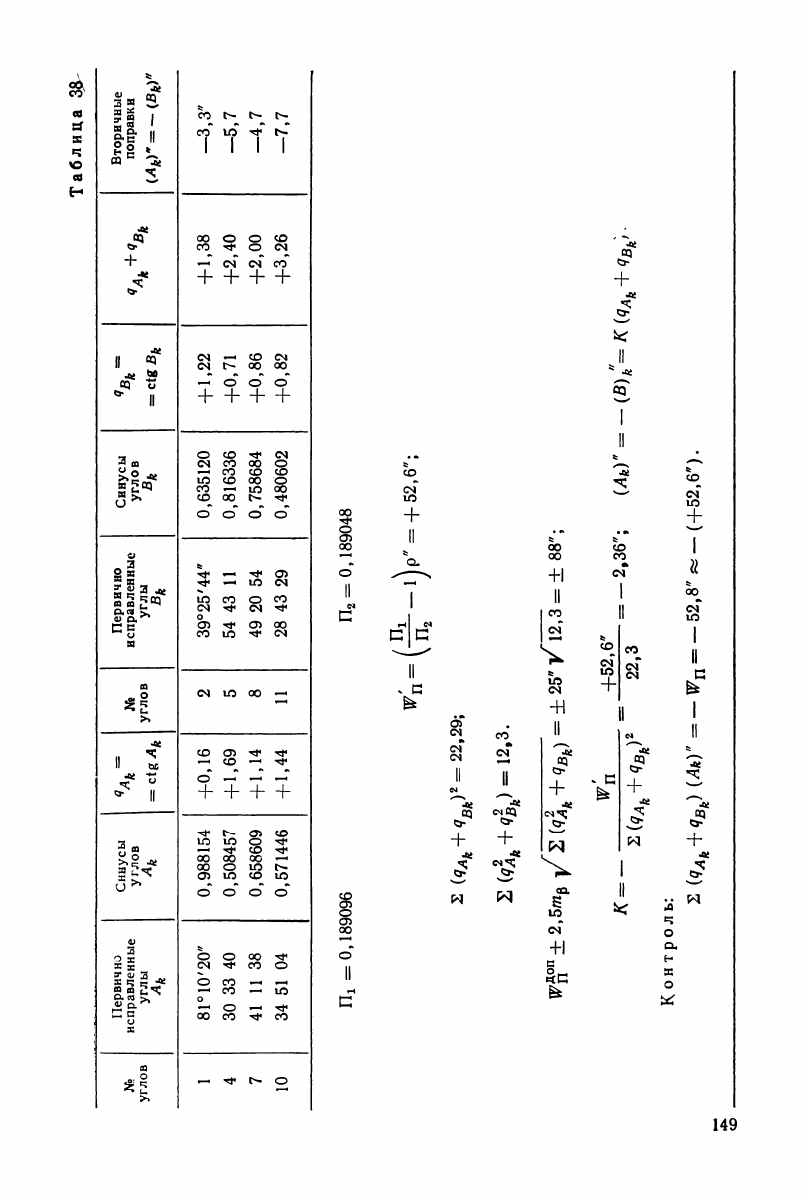
6. Вторичные поправки в связующие углы находят по первично

исправленным углам i' (Ak и Bh). Вычисления производят по фор-

мулам, помещенным в соответствующих местах схемы решения

задачи (табл. 38). Знаками П1 и П

обозначены произведения си-

нусов углов, помещенных в соответствующих столбцах табл. 38,

т. е.

П1

= 0,988154X0,508457Х...Х0,571446 = 0,189096 и др. Отме-

тим, что, если угол (A

или Въ) будет больше 90°, то знак Цак ИЛИ

Цвъ будет отрицательным.

Вторичные поправки выписывают в табл. 36 и вычисляют урав-

ненные углы f". Контроль вычислений: сумма уравненных углов в

треугольнике должна быть равна 180°.

7. По уравненным углам с учетом значения исходной стороны

по теореме синусов вычисляют стороны треугольников. Контроль

решения: вычисленное значение исходной стороны ^1

зыч

не

долж-

но отличаться от заданного более 5 см.

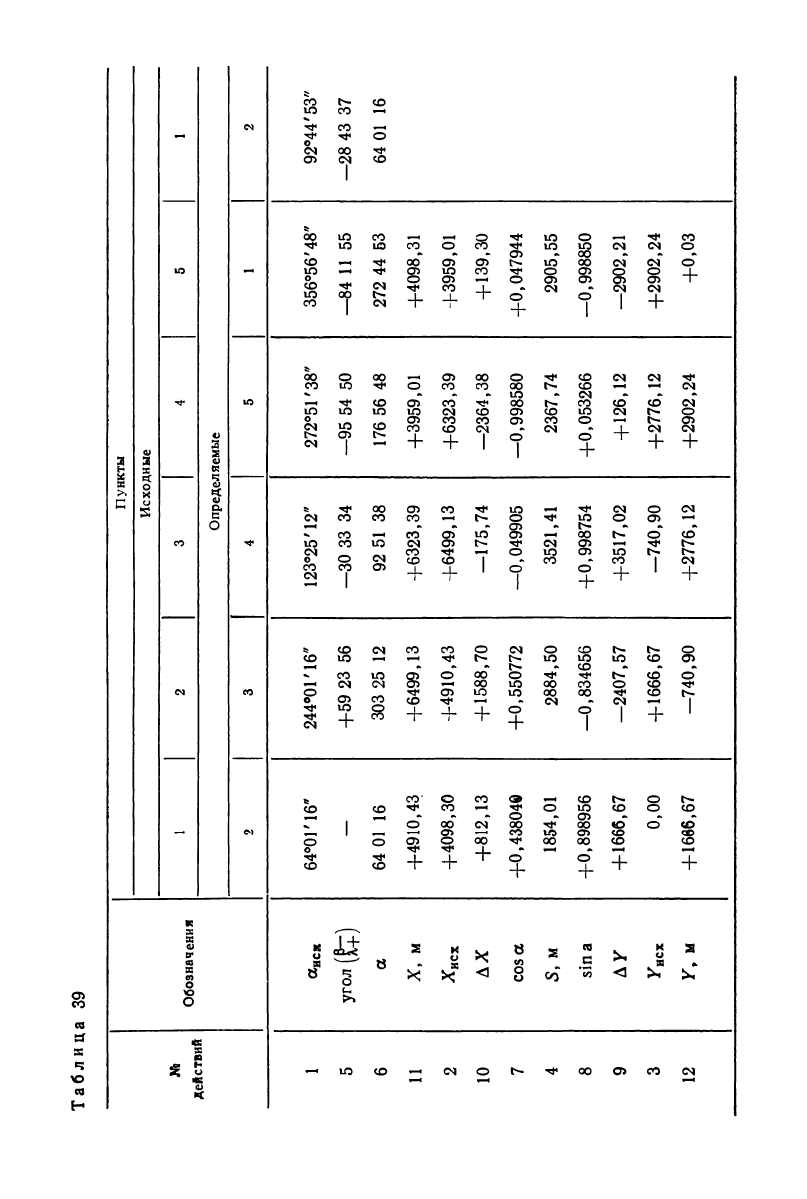
8. Вычисляют координаты пунктов центральной системы, ре-

шая прямую геодезическую задачу. В табл. 39 выписывают исход-

ный дирекционный угол ai-2 = 64°01

и исходные координаты

пункта 1, т. е. Х\ = +4098,30 м и У=0 м. Наметив ходовую линию

1—2—3—4—5—i, вычисляют по данным табл. 36 соответствующие

уравненные углы и обычным путем находят координаты пунктов

Таблица 40

Координаты

Длина

стороны

S, м

Название

пункта

К, м

Y, м

Длина

стороны

S, м

Дирекционные

углы, a

На пункт

+4098,30

0,00

1854,01

2905,55

5212,55

64°0Г16"

92 44 53

342 50 59

+6499,13

—740,90

3521,41

2884,50

5212,55

92 51 38

123 25 12

162 50 59

+6323,39

+2776,12

2367,84

1796,49

3521,41

176 56 48

218 08 21

272 51 38

Примечание: система координат — условная.

геодезической сети. Контроль вычисления координат пунктов: ко-

ординаты исходного пункта 1> полученные в результате решения

задачи, не должны отличаться от заданных более чем на 5 см.

9. Составляют каталог координат пунктов (табл. 40) *, куда

выписывают координаты пунктов центральной системы, дирекцион-

ные углы направлений на один-два смежных пункта и расстояния

до них и другие сведения.

10. Составляют отчетную схему триангуляции 2 разряда в мас-

штабе 1 :25

ООО.

Ее оформление показано на рис. 76.

Уравнивание геодезического четырехугольника

(окончательные вычисления)

В качестве дополнительного примера рассмотрим методику

уравнивания (окончательные вычисления) геодезического четырех-

угольника 2 разряда (рис. 77), в котором 1 и 2 являются исходны-

ми пунктами, а 3 и 4 — определяемыми. Исходные данные в мест-

0,(Г *f

ff +20

-1

0 0

0 4,0 +2,0 +3

}

1-25 000

Рис. 76. Отчетная схема триангуля- Рис. 77. Схема геодезического четы-

дии 2 разряда рехугольника

ной системе координат для решения задачи представлены в

табл. 41.

Таблица 41

Название

пункта

Координаты X, м

У, м

Горизонтальное

проложение 5, м

Дирекционный

угол а

На пункт

7248,61

70286,23

2210,30 313°18'43" 2

8764,81

68677,95

2210,30

133 18 43 1

* В табл. 40 показан сокращенный вариант.

Поправки

№ углов

Измеренные

углы

(О

(0'=

=(оЧ

+(0»

Секунды

исправлен-

ных углов

Поправки

аг

Уравненные

углы 1"

30°04'55"

63 09 58

62 51 12

23 54 11

—4"

—4

+2"

—2

—6

53"

+ 1"

— 1

+ 1

—1

30°04'54"

63 09 55

62 51 07

23 54 04

И^+16"

180 00 16 —16

0 —16

0 180 00 00

30 01 32

63 13 15

54 09 И

33 35 50

—2

+ 1

—1

30 01 34

63 13 15

53 09 17

33 35 54

=-12"

179 59 48

+12

+ 12

180 00 00

30 04 55

—4

—2

(l)i = (2)i

= (3)

= (4)

=—^ =—4";

63 09 58

—4

—2

(5)i = (6)i

=(7)1 = (8)1=--2-=-)-3";

53 09 И

33 35 50

+з

Щ =1F3+(1)1 + (2)I + (7)I + (8)I =

=—6"—2"=—8";

(1)П = (2)П = (7 )П=»(8)П=-

+з

Г* »

=-6"

179°59'54"

—2"

+8"

+6"

(3)П = (4) п = (5)И

=(6) II—2=—2";

Ниже, в таблицах 42, 43, 44, приводятся результаты уравнива-

ния геодезического четырехугольника. Необходимые для вычисле-

ния формулы приведены в соответствующих местах схем решения

задачи. Их смысл соответствует данным, подробное описание ко-

торых приведено в § 43.

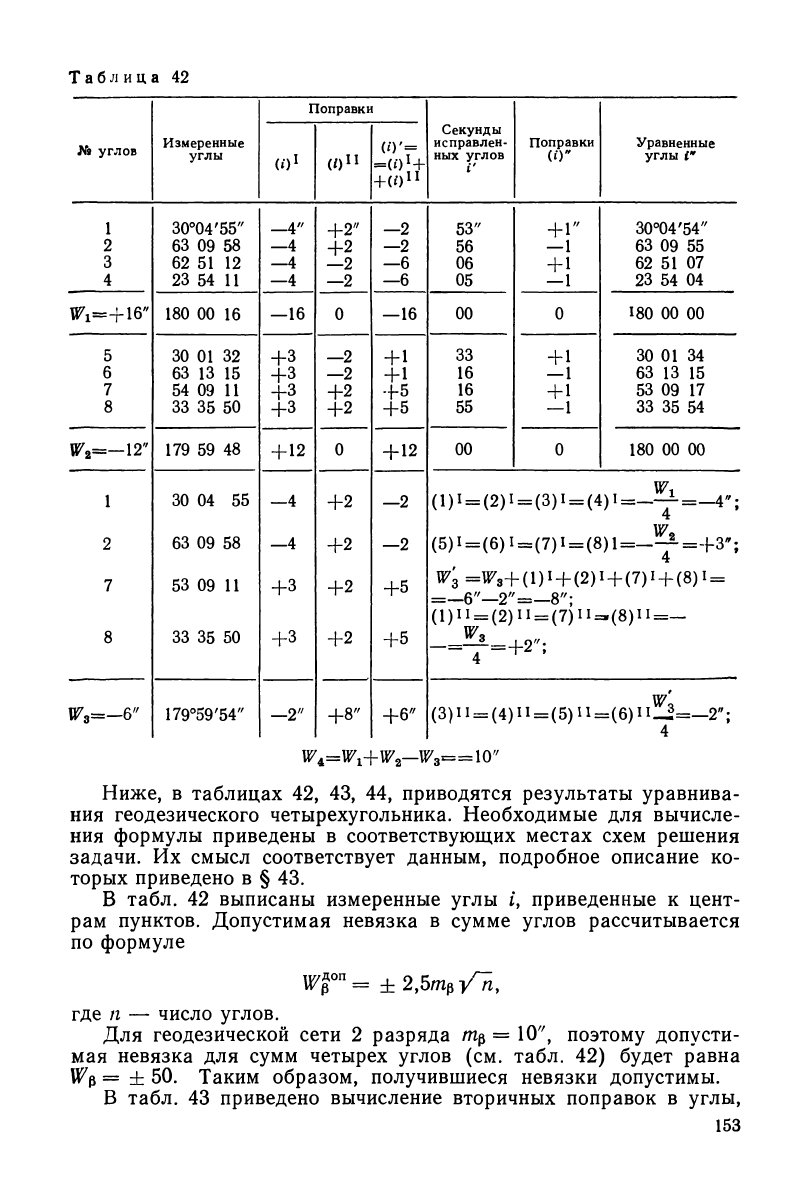
В табл. 42 выписаны измеренные углы i, приведенные к цент-

рам пунктов. Допустимая невязка в сумме углов рассчитывается

по формуле

Wr= ±2,5т

уЧ

где я — число углов.

Для геодезической сети 2 разряда = 10", поэтому допусти-

мая невязка для сумм четырех углов (см. табл. 42) будет равна

= ± 50. Таким образом, получившиеся невязки допустимы.

В табл. 43 приведено вычисление вторичных поправок в углы,

№

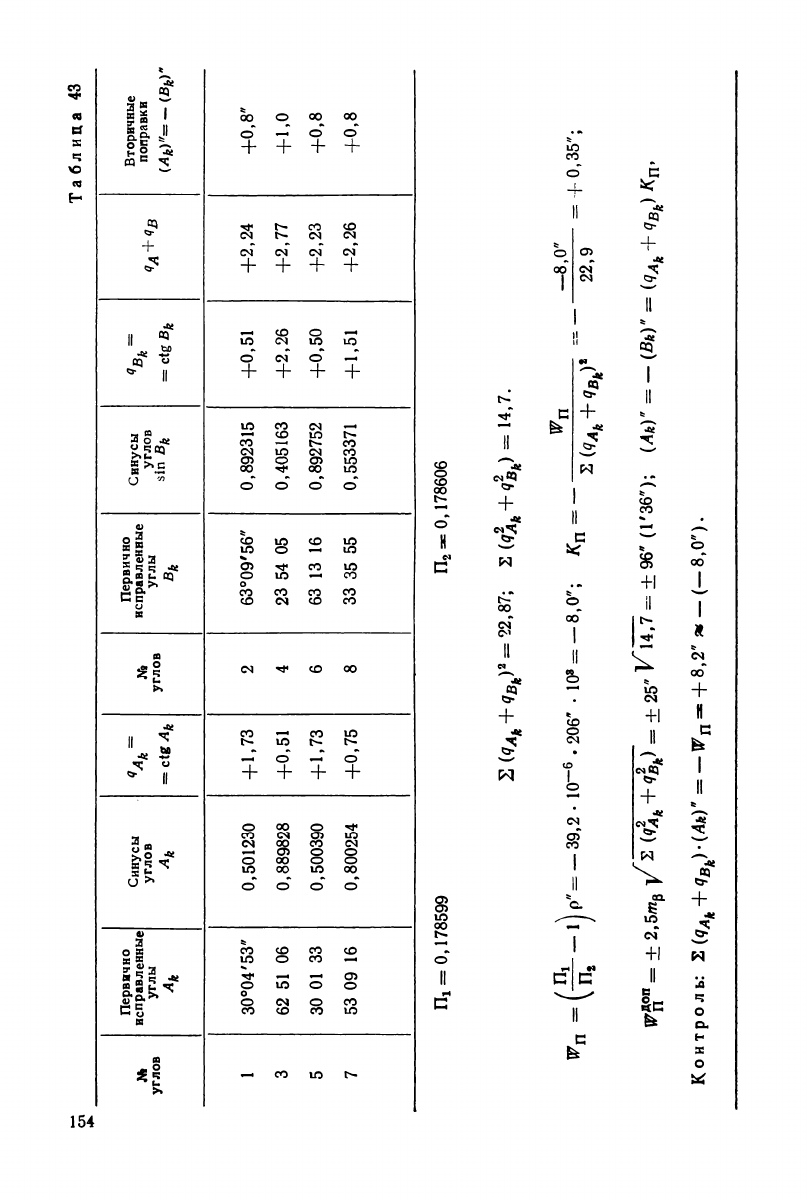
углов

Первично

исправленные

углы

Синусы

углов

= ctg

№

углов

Первично

исправленные

углы

Синусы

углов

sin

Bfr

Q D =

= ctg

iA +

Вторичные

поправки

)»=-(B

1 30

04'53"

0,501230

+ 1,73 2

63°09'56"

0,892315

+0,51

+2,24

+0,8"

62 51 06

0,889828 +0,51

23 54 05

0,405163

+2,26

+2,77

+1,0

5 30 01 33

0,500390

+1,73

63 13 16

0,892752 +0,50

+2,23

+0,8

53 09 16

0,800254 +0,75

33 35 55

0,553371

+ 1,51

+2,26

+0,8

= 0,178599 П

=»=

0,178606

2 (Я

Аь

+ Я

Вь

)

; 2 (А + Л ) = 14,7.

/ П \ t^n Я О"

( пГ ~ ')

10-6

" '

103 =

'°"

;

*П~

-—^-+0.35';

Я К

яоп _

± 25Жр

/ 2 (<7^+«7|

)

+ 25" V\AJ = ± 96" (l'36")

;

)" = - (B

)" = + q

) K

Контроль: 2(^ + »

Ва

)-(Л»)'=--Г

-+8,2' »-(-8,0").

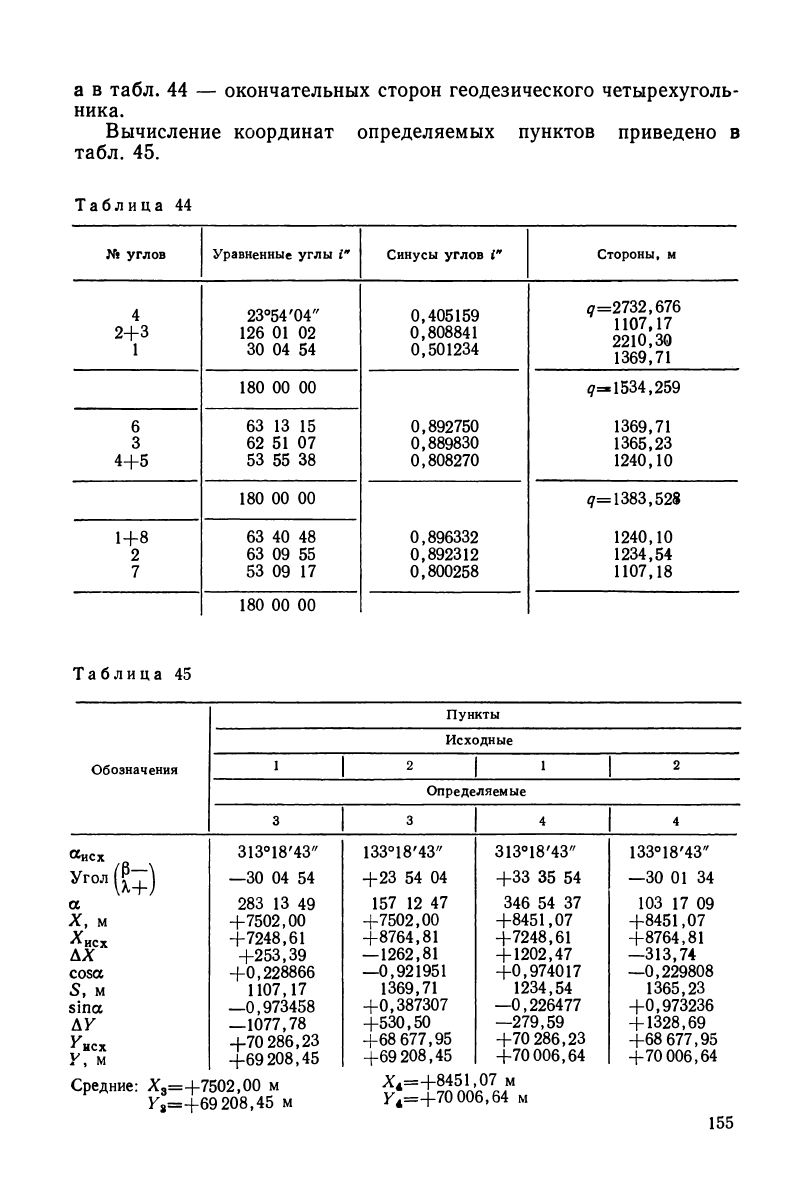
а в табл. 44 — окончательных сторон геодезического четырехуголь-

ника.

Вычисление координат определяемых пунктов приведено в

табл. 45.

Таблица 44

№ углов

Уравненные углы i"

Синусы углов V

Стороны, м

2+3

23°54'04"

126 01 02

30 04 54

0,405159

0,808841

0,501234

(7=2732,676

1107,17

2210,30

1369,71

180 00 00 <7=1534,259

4+5

63 13 15

62 51 07

53 55 38

0,892750

0,889830

0,808270

1369,71

1365,23

1240,10

180 00 00

<7=1383,528

1+8

63 40 48

63 09 55

53 09 17

0,896332

0,892312

0,800258

1240,10

1234,54

1107,18

180 00 00

Таблица 45

Обозначения

Пункты

Исходные

Определяемые

исх

Угол(Р-)

X, м

сх

cosa

5, м

sina

^нсх

У у м

313°18'43"

—30 04 54

283 13 49

+7502,00

+7248,61

+253,39

+0,228866

1107,17

—0,973458

—1077,78

+70 286,23

+69 208,45

Средние: Х

=+7502,00 м

=+69208,45 м

133°18'43"

+23 54 04

157 12 47

+7502,00

+8764,81

—1262,81

—0,921951

1369,71

+0,387307

+530,50

+68 677,95

+69 208,45

313°18'43"

+33 35 54

346 54 37

+8451,07

+7248,61

+ 1202,47

+0,974017

1234,54

—0,226477

—279,59

+70 286,23

+70 006,64

=+8451,07 м

=+70 006,64 м

133° 18'43"

—30 01 34

103 17 09

+8451,07

+8764,81

—313,74

—0,229808

1365,23

+0,973236

+ 1328,69

+68 677,95

+70 006,64

§ 44. ВЫСОТНАЯ ГЕОДЕЗИЧЕСКАЯ СЕТЬ СГУЩЕНИЯ

Высотная геодезическая сеть сгущения строится путем проло-

жения ходов технического нивелирования по пунктам съемочного

обоснования (геодезических сетей сгущения и съемочных сетей).

Нивелирование производится по способу из середины, расстоя-

ние от прибора до реек не должно превышать 150 м при благо-

приятных условиях наблюдений. Неравенство плеч на станции до-

пускается до 10 м, расстояние от прибора до реек измеряют шага-

ми или нитяным дальномером. Работают обычно с двусторонними

нивелирными рейками.

После установки прибора в рабочее положение наблюдение на

станции производят в следующем порядке:

отсчет по черной стороне задней рейки (1),

отсчет по черной стороне передней рейки (2),

отсчет по красной стороне передней рейки (3),

отсчет по красной стороне задней рейки (4).

Отсчеты, неравенство высот нулей реек, а также превышения

записывают в журнал (табл. 46).

Вычисляют неравенство высот нулей реек (5) и (6), а затем

превышения (7) и (8). Среднее превышение в камеральных усло-

виях записывают чернилами.

Таблица 46

Журнал технического нивелирования

Дата 20. VII. 1984 г. Погода: ясно

№ точек

Отсчет по рейке

Среднее

превышение,

мм

№

станции расстояние

в метрах

задняя

передняя

Превышение,

мм

Среднее

превышение,

мм

Ход пункт 1 — пункт 3

пункт 1—2

130

0840 (1)

5625 (4)

4785 (5)

0885 (2)

5665 (3)

4780 (6)

-45 (7)

-40 (8)

—42

1780

2760

—980

2—X

6567

7549 —982

—981

100

4787

4789

Контроль-

ные вычис-

ления

2з = 21 558 (9), 2Л = —2545 (13), 2А

СР

— 24 103 (10), — = — 1272 (14),

2з — 2

= — 2545 (И),

2э — 2

п =

_ 1272 (12).

: — 1272 (15).

№

пункта

Измеренное

превышение,

мм

Число

штативов

Поправки,

мм

Исправлен-

ное

превышение,

мм

Высота, м

108,054

— 1885

—1882

106,172

— 1880

—1877

104,295

+ 1254 6

+ 1259

+ 1254

105,554

+4002

+4008

+4002

109,562

2Л

ПВ

= + 1491

+17

+ 1508

Жеор = + 1508, /

= — 17 мм, /J

= ± 10 У 22= ±47 мм.

Для контроля определения превышений на станции сравнива-

ют их значения, полученные по черным и красным сторонам реек.

Расхождение допускается не более 5 мм.

При работе с односторонними нивелирными рейками превыше-

ние на станции определяют при двух горизонтах прибора.

Камеральная обработка результатов измере-

ний

1. Проводится постраничный контроль. Складывают задние

) (9) и передние (2

) (10) отсчеты, записанные в журнале на

каждой странице. Далее производят действия (И), (12), (13),

(14) и (15). Контролем служит равенство чисел (12), (14) и (15)

в пределах ошибок округлений при вычислениях.

2. Составляется схема высотного съемочного обоснования, где

показывают: средние превышения со своим знаком и направление

(стрелкой), к которому они относятся; длину сторон между точ-

ками съемочного обоснования (в км) и число станций при ниве-

лировании каждой линии; невязки в каждом полигоне и их допус-

тимую величину, которую вычисляют по формуле

= ±50/1 мм

или

/Г= ± 10/п мм*,

где L — число километров в ходе или полигоне; п — число стан-

ций в ходе или полигоне.

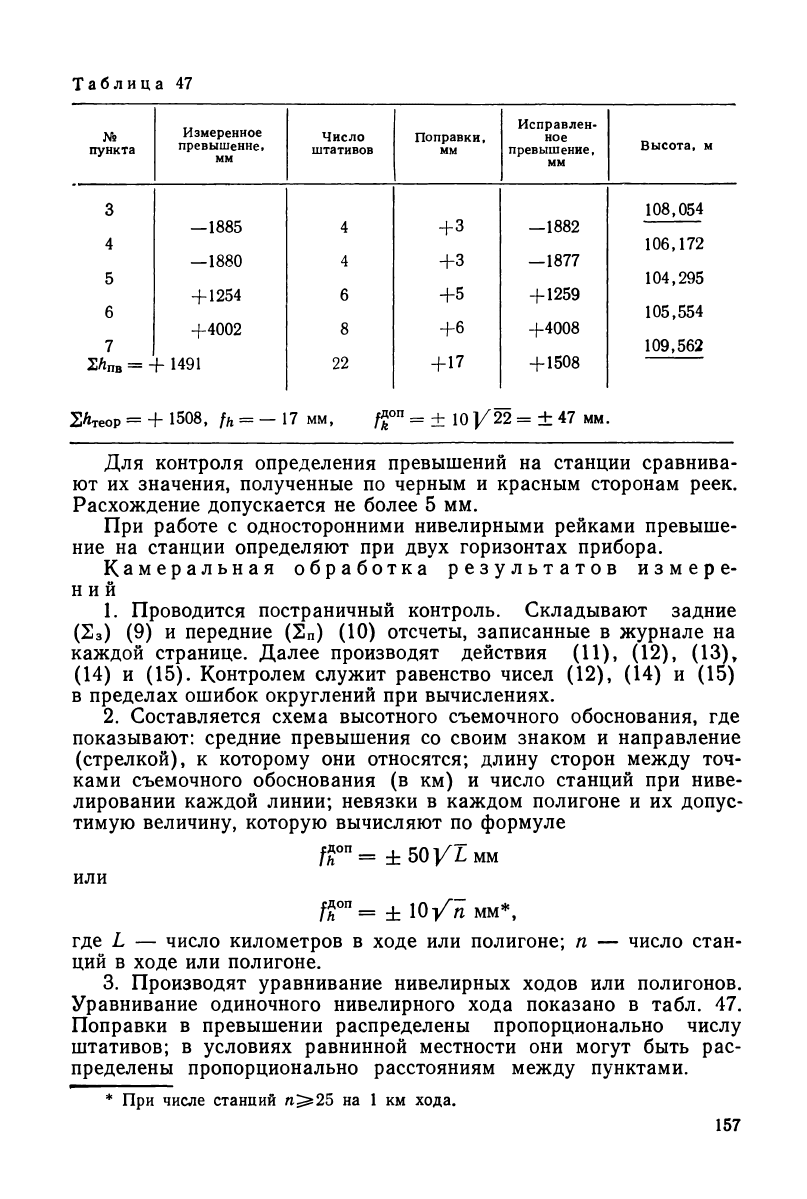
3. Производят уравнивание нивелирных ходов или полигонов.

Уравнивание одиночного нивелирного хода показано в табл. 47.

Поправки в превышении распределены пропорционально числу

штативов; в условиях равнинной местности они могут быть рас-

пределены пропорционально расстояниям между пунктами.

* При числе станций п^25 на 1 км хода.