Неумывакин Ю.К., Смирнов А.С. Практикум по геодезии
Подождите немного. Документ загружается.


Решение на ЭКВМ БЗ-37
Порядок нажатия
клавиш и ввода чисел
Результат в регист-
ре индикатора
Буквенные обозначения величин,
показанных на индикаторе
22 [Т]
П +
Х
2
[+]
22
е
1
11 (Т) п
+
Х
2
f+l
33
8i +е
2
з [F]
П
+ Х
2
[+j
36
ei + е
2
+ е
3
26 [Tj П+Х
2
|Tj
62
ei + е
2
+ е
3
+ е
4
29 F1
П +
Х
2
[Г]
91 ei + е
2
+ е
3
+ е
4
+ е
б
4
95
[ej =
ei
+e
2
+8
3
+e
4
+e
5
+e
e
60
15,833333 0 = [8
l
] :N
S
6
N
а
94,999998
NQ
1504,1666
N№
0ип[Т]
642,8334
[e?[ — NW
128,56668 m
2
= ([e^] — NQ
2
) : (N — 1>
11,338724
m = Vm
2
28,34681
2,5 • m
•Шг^Н
11,572535
2,5 • m/N
Таким образом,
9 = -М-
=
-iiL «
+
16 мм;
m
= V
[e
lZT мм;
I
8
I
« 16
ММ
> =—7^ « 12 мм.
II
у 6
Результаты вычислений показывают, что полученная оценка 9
значима. При этом величина систематической погрешности, прихо-
дящаяся на одно уложение ленты, равна поправке за компариро-
вание 6
К
, но имеет противоположный знак.
Действительно, при измерении 120-метрового компаратора
20-метровой лентой число полных уложений п=6. Тогда в :
лг
=
= 16 : 6^2,7 мм, а поправка за компарирование
6* = = ^
ист
~
Гср
=
115
~~
131
« — 2,7 мм.
п п б

§ 8. ОЦЕНКА ТОЧНОСТИ ПО РЕЗУЛЬТАТАМ МНОГОКРАТНЫХ
РАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ И ТОЙ ЖЕ ВЕЛИЧИНЫ
Если при исследовании точности измерений истинное значение
величины неизвестно, то получают п равноточных результатов
измерений х
и
x
2l
х
п
и сравнивают их со средним арифметиче-
ским значением
Среднюю квадратическую погрешность одного измерения рассчи-
тывают по формуле
, = у Ж = ушЦК.
(19)
т
п— 1
При вычислении на ЭКВМ для решения такой задачи удобно
использовать формулу
т =
/
У
К-1
п— 1
(20)
Пример. Для исследования точности теодолита ТЗО получено 5 резуль-
татов измерений одного и того же горизонтального угла: 103
о
25,5'; 103°26,0';
103°25,5'; 103°26,5'; 103
о
26,0'.
Вычислить среднюю квадратическую погрешность одного измерения.
Указание: при решении подобных задач целые значения величин, оди-
наковые для всех результатов, обычно отбрасывают (в данном случае такой
величиной является 103°20').
Решение на ЭКВМ Б3-37
Порядок нажатия клавиш
и ввода чисел
Результат в регист-
ре индикатора
Буквенные обозначения величин,
показанных на индикаторе
5
0
5
В^ 0
6
0^ 0
«В'0^0
6 И 5 0,01^0
6
0Д^
2
Ш
5 ЕД
00
0^0
<0
Х
Г
+
ХО
x
i +
х
г +
х
з
Х
1 + Xi +х
3
+ x
t
l
x
lY = x
1
+x
2
+x
3
+x
l
+x
6
P = [*,]'
:
n
[XiV
[
Xl
Y : n
l
x
jl - [Xif : n
([*?] — l
x
i]
2
'• n) • (1-1) =m
2
m = V^m
2

х = 103°20' + JSll = Ю3°20' + 103°25,9';
п 5
— = 1/ — = 0,42 « 0,4'.
п—
1
|/ 4
§ 9. ОЦЕНКА ТОЧНОСТИ УГЛОВЫХ ИЗМЕРЕНИЙ ПО НЕВЯЗКАМ
В ПОЛИГОНАХ И ХОДАХ
Для оценки точности по результатам массовых угловых измере-
ний используют невязки /
г
-, полученные при проложении полигоно-
метрических и теодолитных ходов (полигонов).
Среднюю квадратическую погрешность измерения одного угла
вычисляют по формуле
Щ =
/[1
" N
(21)
где п—число углов в i-м ходе или полигоне (/=1, 2, ..., N);
N — число ходов или полигонов, для которых известны значения
угловых невязок f{.
Пример. Вычислить среднюю квадратическую погрешность измерения
угла по 5 значениям невязок теодолитных ходов: fi = + l»8', 18; /2=—2,4',
п
2
= 30; /
3
=—2,5', я
3
=25; /
4
=+3,0', я
4
= 14; /
5
= —3,2', п
5
= 25.
По формуле (16) рассчитать точность полученной оценки и соответственно
округлить окончательный результат.
Решение на ЭКВМ БЗ-37
Порядок нажатия клавиш и ввода
чисел
Результат
в регистре
индикатора
Буквенные обозначения
величин, показанных на
индикаторе
1 |Т]80
И
а
18
0
0,18
п
: tii
2 040
0
0
30 0 02
0,192
fl
: n
2
2 050
0
0
25 0 0 0,25
fl
: n
3
30
0
0
14 0 0nj__
0,6428571
fl
: tii
3020
В
0
25
0 Шд^
0,4096
fl
' n
b
0
ИП
0
1,6744571
\f\
щ\
50
0,3348914
m
p
=
\f]
•
n
i\ '
: N
0 0,578698
m
p
10
0,1830003
m
m
p
=
: y~2N

§ 10. ОЦЕНКА ТОЧНОСТИ ПО РАЗНОСТЯМ ДВОЙНЫХ
РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
В данном случае аргументами для оценки точности являются
результаты повторных (парных) измерений величин и их разности
При отсутствии систематических погрешностей среднюю квадра-
тическую погрешность рассчитывают по формуле
где п — число парных измерений и их разностей d.
Пример. В табл. 6 приведено 6 парных измерений горизонтальных углов
полным приемом (при положении КП и KJI). Вычислить среднюю квадратиче-
скую погрешность измерения угла одним полуприемом.
Таблица 6
d
1
= x
1
—x
l
, d
2
= x
2
— x
2
, d
n
= x
n
— x
l
п-
2 п
(22)
Результаты
№
измерений
при КП
при КЛ
2
3
4
5
6
164°52
238 01
186 36
94 12
205 48
79 16
164°53
238 01
186 34
94 12
205 49
79 15
— 1
0
+2
0
— 1
4-1
0
4
0
Суммы 4-1
7
Решение (вычисления выполнены устным счетом в табл. 6).
Если в результатах измерений заведомо ожидается наличие
систематической погрешности, то среднюю квадратическую погреш-

ность т и оценку средней систематической погрешности 0 рассчи-
тывают по формулам
т = ~\/ ; ё = -Ж. (23)
У 2 (п — 1) п
V
Значимость систематической погрешности определяют на основании
критерия (18).
Пример. При исследовании коллимационной ошибки теодолита ТЗО вы-
полнены парные наблюдения (при КП и КЛ) на 8 целей. Полученные отсчеты
приведены в табл. 7.
Таблица 7
№ точек
наблюдения
Отс
П
четы
л
d. = n
—
Л,
мин
<
1 16°16'
13'
+3
9
2
29 32
30
+2
4
3
44 46
45
+ 1
1
4
75 52
50
+2
4
5
116 21
19
+2
4
6
133 27
25
+2
4
7
141 14
11 +3
9
8
179 39
37
+2
4
Суммы
+17
39
Вычислить оценку средней систематической погрешности и среднюю квад-
ратическую погрешность измерения одного направления. Определить значимость
систематической погрешности; при этом иметь в виду, что значимая величина 9
соответствует среднему значению двойной коллимационной ошибки для данного
теодолита.
Решение (вычисления выполнены устным счетом в табл. 7).
0== + w+2';
п 8
-,/ [d?]-/i6
2
,/"39-35
Следовательно, полученная величина двойной коллимационной ошибки зна-
чима.
§ 11. ОЦЕНКА ТОЧНОСТИ ПО РАЗНОСТЯМ ДВОЙНЫХ
НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При выполнении некоторых видов геодезических работ (напри-
мер, при измерении линий лентой в теодолитных ходах) образуют-
ся ряды парных (двойных) измерений, причем отдельные пары
32
получены в различных друг от друга условиях, г. е. неравноточны
между собой. Точность таких измерений оценивают с учетом их
весов и характеризуют средней квадратической погрешностью та-
кого измерения, вес которого равен единице (сокращенно — средней
квадратической погрешностью единицы веса ^х).
При отсутствии систематических погрешностей среднюю квадра-
тическую погрешность единицы веса рассчитывают по формуле
где pi — вес, характеризующий относительную точность i-й пары
измерений (t = l, 2, ..., п)\ * п — число двойных измерений в данном
ряду.
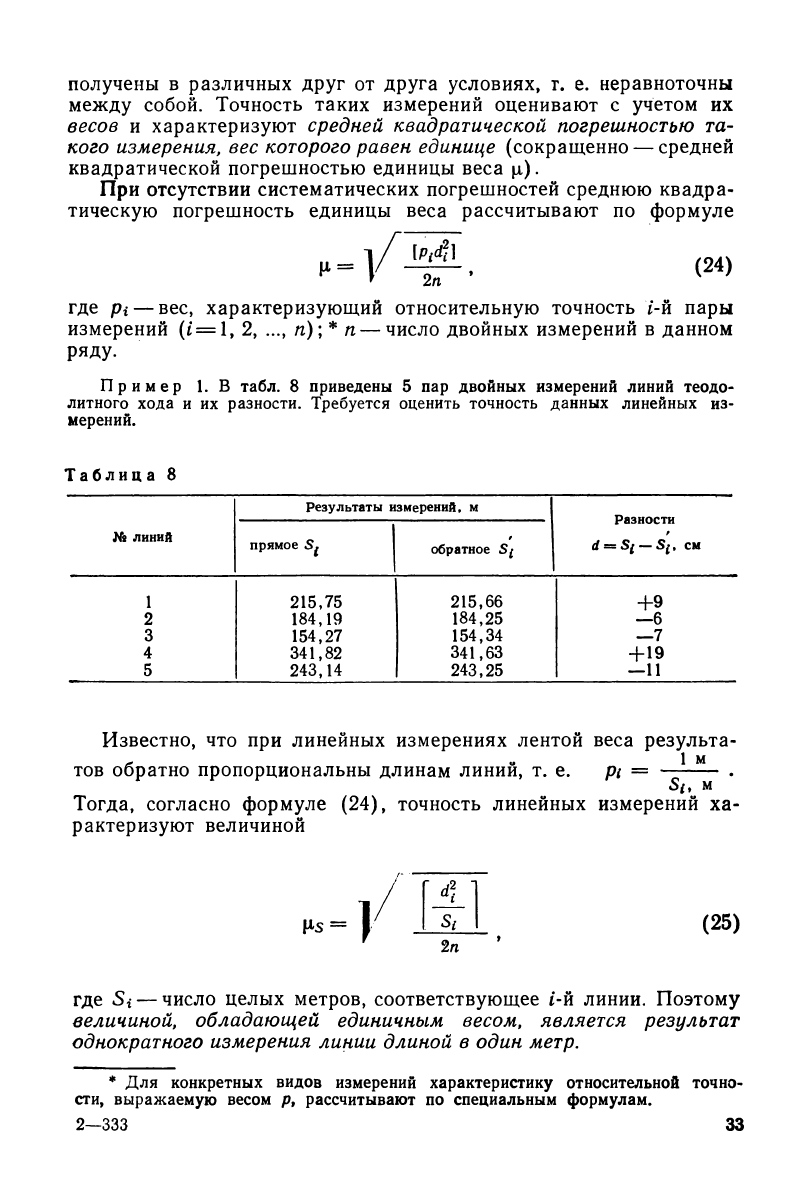
Пример 1. В табл. 8 приведены 5 пар двойных измерений линий теодо-
литного хода и их разности. Требуется оценить точность данных линейных из-
мерений.
Таблица 8
Результаты измерений, м
Разности
№ линий
прямое 5^
обратное Sj
d = S{ —St, см
1
215,75
215,66
+9
2 184,19
184,25
—6
3
154,27
154,34 —7
4
341,82
341,63
+ 19
5
243,14
243,25
—11
Известно, что при линейных измерениях лентой веса результа-
* „1м
тов обратно пропорциональны длинам линии, т. е. pi = .
S{
t
м
Тогда, согласно формуле (24), точность линейных измерений ха-
рактеризуют величиной
1
±
Sj
2 п
(25)
где Si — число целых метров, соответствующее /-й линии. Поэтому
величиной, обладающей единичным весом, является результат
однократного измерения линии длиной в один метр.
* Для конкретных видов измерений характеристику относительной точно-
сти, выражаемую весом р, рассчитывают по специальным формулам.
2—333 33

Решение на ЭКВМ БЗ-37
Порядок нажатия клавиш и
ввода чисел
Результат
в регистре
индикатора
Буквенные обозначения
величин, показанных на
индикаторе
8
ВВЕ]
21
Е
0,375
d
2
[
:S
1
4
00Ш
6
0
0,1956521
d\ : S
a
»a sis «seal,
0,3181818 d\ : S
3
0,0555555
d> : S
4
0,4979423
2,4423317
I df : S
t
]
,00
0,2442331
И-S
= [4 : S
{
] : 2*
0,4941994
^S = Vvl
\is ~ V 2,44:10 » 0,49 см « 0,005 м.
Полученное значение jis позволяет вычислить среднюю квадра-
тическую погрешность любой длины линии Si, измеренной при дан-
ных условиях, по формуле
ms^lisVSi. (26)
Так, для линии Ss~243 м средняя квадратическая погрешность
однократного измерения:
m
s
= 0,005К243 « 0,08 м.
Пример 2. В табл. 9 приведено 5 результатов определения площадей
треугольников на плане (в см
2
). Площадь каждого треугольника определена
дважды — по измерениям двух различных оснований и высот. Требуется оце-
нить точность измерения площади.
Таблица 9
Площади, см
2
No
Разности
No
t
треугольников
p
'i
d^P.-Pf си'-IO-
2
1
20 >53
20,61
—8
2 6,21 6,17
+4
3
15,20
15,15
+5
4
25,03
24,96
+7
5
16,78
16,84
—6
Известно, что при данном способе измерения площадей фигур на плане веса
результатов обратно пропорциональны размерам площади, т. е. pi = \/Pi. Тогда
Ц
Р
= л/ [
d
^
,Pi
1 . (27>
Г 2п
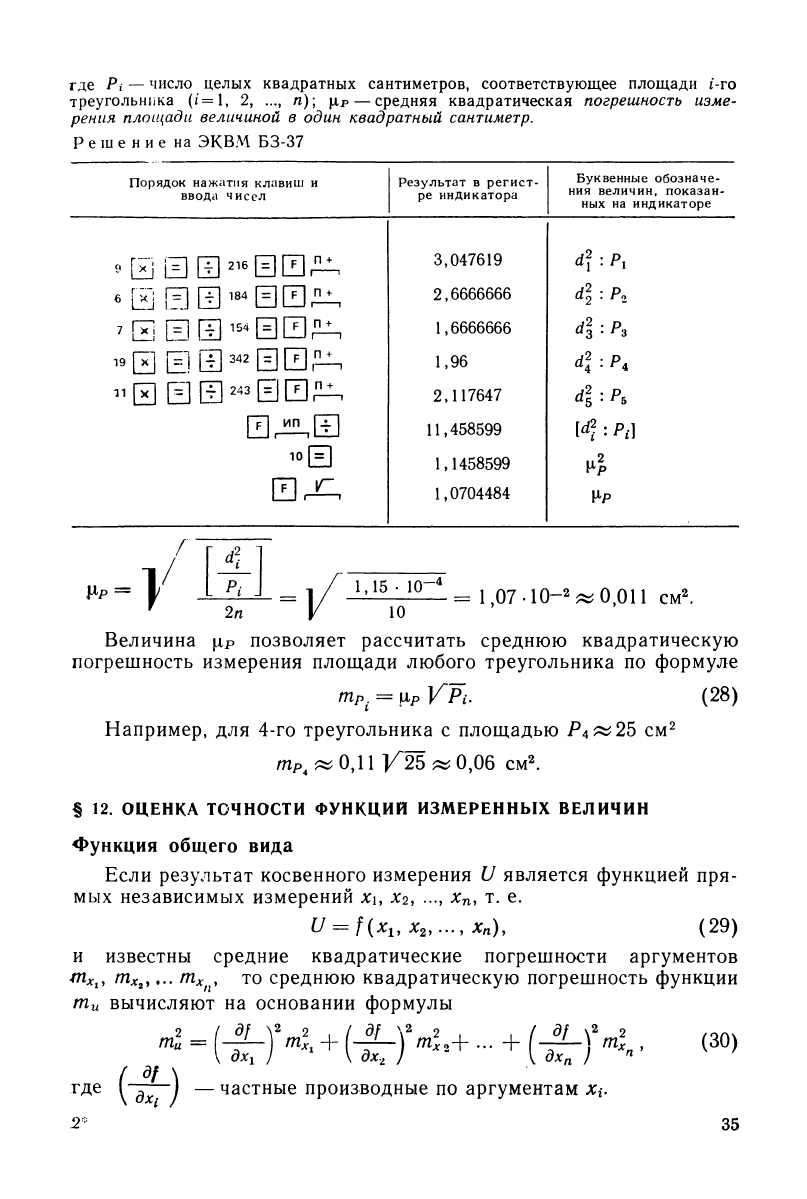
где Pi — число целых квадратных сантиметров, соответствующее площади i-го
треугольника (/=1, 2, ..., п)\
(Ыр
— средняя квадратическая погрешность изме-
рения площади величиной в один квадратный сантиметр.
Решение на ЭКВМ БЗ-37
Порядок нажатия клавиш и
ввода чисел
Результат в регист-
ре индикатора
Буквенные обозначе-
ния величин, показан-
ных на индикаторе
9
3,047619
PI
6
В
2,6666666
4:
Р2
7
Е
1,6666666
Р
3
19
И
Ei Ш
342
0 0 ^
1,96
РА
11
0
2,117647
Ф
Рь
Шг^РП
11,458599
10
0
1,1458599
А
1,0704484
ИР
b
1
я =
}
/
15 • Ю-
4
= 1,07- Ю-
2
«0,011 см
2
.
2 п V Ю
Величина jup позволяет рассчитать среднюю квадратическую
погрешность измерения площади любого треугольника по формуле
m
P
. = iip УРс. (28)
Например, для 4-го треугольника с площадью Р
4
~ 25 см
2
гпр
4
& 0,11 У 25 « 0,06 см
2
.
§ 12. ОЦЕНКА ТОЧНОСТИ ФУНКЦИЙ ИЗМЕРЕННЫХ ВЕЛИЧИН
Функция общего вида
Если результат косвенного измерения U является функцией пря-
мых независимых измерений хи Хч, х
п
, т. е.
U = f{Xi, х
2
,...,Хп), (29)
и известны средние квадратические погрешности аргументов
*Пх
1У
гпх
2
,... m
XnJ
то среднюю квадратическую погрешность функции
пг
и
вычисляют на основании формулы
ml =
df
m
mU+... +
(JL
df \2 2
dxi ) \ dx
2
J
ЛЛ
' V дх
п
)
(
d
t \
где ^
dx
J —частные производные по аргументам Х\.
2"'
(30)
35

Пример 1. Рассчитать среднюю квадратическую погрешность треугольни-
ка по измеренным на плане основанию а=6,48 см и высоте А=8,17 см, если
средние квадратические погрешности т
а
= тк=0,02 см.
В соответствии с условиями задачи функция (29) имеет вид
Р = — ah.
2
Согласно формуле (30), =
т
а +
т
\-
дР 1 дР 1
Так как частные ппоизводные = h и —— = а,
да 2 dh 2
X 10~
4
+ 8,2
2
• Ю-
4
= (42,25+ 67,24) . КГ
4
= 109 . Ю""
4
.
Следовательно, т
Р
= "|/l09 • 10~
4
« 0,10 см
2
.
Пример 2. Вычислить среднюю квадратическую погрешность определе-
ния превышения методом тригонометрического нивелирования по измеренным
расстоянию 5=168 м и углу наклона v = —1°46', если ms=0,4 ми m
v
= 1,0'.
В соответствии с условиями задачи (при наведении визирной оси на вы-
соту прибора) функция (29) имеет вид h=Stgv. Тогда, согласно формуле (30)„
*
где —— —выражение угловой погрешности в радианнои мере. Так как част-
р'
ные производные
dh dh
= t
g
v и
dS dv cos
2
v
TO
( S
m
'»Y / 170
•
Г \2 ,
ml = (tg v *
s
>. + [—
•
— ) = (0,031 • 0,4)> + (-j^) =2,6- НГ*.
Тогда
m
h
= V26 • 10~
4
«0,05 M.
Пример 3. Рассчитать среднюю квадратическую погрешность нанесения
контурной точки А полярным методом на плане масштаба 1:5000, если 5=»
= 120 м, погрешность расстояния ms=0,4 м и погрешность построений угла
транспортиром тр — 7'.
Для составления функции (29) примем полярную ось за ось абсцисс в
системе прямоугольных координат, где XA=«S-COS(J; /A=5-SINP.
Тогда, согласно формуле (30),
2
т
х
2
т
2

Так как среднюю квадратическую погрешность положения точки
начала координат (полюса) рассчитывают по формуле
гид = )/ т\ + т
2
у
,
то с учетом равенства (31)
Подставив в формулу (33) числовые значения, получим
/
[ 120
•
7' \2
Функция линейного вида
Если функция имеет вид
и = k
x
x
x
+ k
2
x
2
+ ... + k
n
x
n
+ с, (34)
где к\, /с
2
, к
п
, с — постоянные величины, то частные производ-
ные равны коэффициентам /с* при переменных Х{ и формула (30)
получает выражение
т
Ь = *Wx
x
+
k
Wx
t
+
• • •
+
k
l
m
l
n
•
(35)
Пример 1. Вычислить среднюю квадратическую погрешность определения
расстояния нитяным дальномером теодолита ТЗО, если погрешность дальномер-
ного отсчета mi = 0,3 см, а коэффициент дальномера безошибочен.
Так как определяемое расстояние вычисляют по формуле d=kl+c, где
&=100 и с=0, то выражение (35) имеет вид rrid=kmi. Подставив в него чис-
ловые данные, получим та = 100-0,3=30 см = 0,3 м.
Пример 2. Вычислить среднюю квадратическую погрешность длины линии
D = 241,08 м, если при ее измерении 20-метровой лентой средняя квадратиче-
ская погрешность одного уложения mi—2 см.
В этом случае функция (34) имеет вид D=l\ + l
2
+... + l
n
-\-r
y
где л=12 — чис-
ло полных уложений.
2 2 2 2
Тогда, в соответствии с (35), tn
D
=
m
i
l
=
m
/
8
+ • • • ~f~
m
z (погрешность
остатка г можно не учитывать). Так как m^ = т^ = ... = т^ = mi, то
m
2
D
= nm]
t или то = т
Yn . (36)
Подставив в (36) числовые значения, получим тр = 2 см 1^12^7 см.
Пример 3. Вычислить среднюю квадратическую погрешность разности
d двух результатов измерения горизонтального угла теодолитом Т5, полученных
при положениях КП и КЛ, если средняя квадрэтическая погрешность каждого
полуприема т^ =т^=т = 8".
Так как функция (34) имеет вид d= П—Л, то = или
m
d
= m V~2. (37)
Подставив в (37) числовые значения, получим т^ = 8" 1/2^ И".
Формула (37) иллюстрирует общую закономерность, согласно
которой средняя квадратическая погрешность алгебраической сум-
А относительно
(32)
(33)
