Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1

Подождите немного. Документ загружается.

111

Êîëè÷åñòâåííûìè ïîêàçàòåëÿìè èçíîñà ìîãóò áûòü ëèíåéíûé èçíîñ

(èçìåíåíèå ðàçìåðà òåëà â íàïðàâëåíèè, ïåðïåíäèêóëÿðíîì ïîâåðõíîñòè

òðåíèÿ), ñêîðîñòü èçíàøèâàíèÿ (èçìåíåíèå ëèíåéíîãî èçíîñà â åäèíèöó

âðåìåíè) è èíòåíñèâíîñòü èçíàøèâàíèÿ (îòíîøåíèå ëèíåéíîãî èçíîñà ê

ïóòè òðåíèÿ). Çàêîí èçíàøèâàíèÿ â îáùåì ñëó÷àå äîëæåí âûðàæàòü çàâè-

ñèìîñòü ëèíåéíîãî èçíîñà èëè ñêîðîñòè èçíàøèâàíèÿ îò ñèëîâûõ è êèíå-

ìàòè÷åñêèõ ïàðàìåòðîâ (â ïåðâóþ î÷åðåäü äàâëåíèÿ íà ïîâåðõíîñòè òðå-

íèÿ è ñêîðîñòè îòíîñèòåëüíîãî ñêîëüæåíèÿ), îò ïàðàìåòðîâ, õàðàêòåðè-

çóþùèõ ñîñòàâ, ñòðóêòóðó è ìåõàíè÷åñêèå ñâîéñòâà ìàòåðèàëîâ òðóùåéñÿ

ïàðû (òâåðäîñòè, ïðåäåëà òåêó÷åñòè, ìîäóëÿ óïðóãîñòè è äð.), îò ñâîéñòâ

ïîâåðõíîñòíîãî ñëîÿ (øåðîõîâàòîñòè, æåñòêîñòè, íàïðÿæåííîãî ñîñòîÿíèÿ

è äð.), îò âèäà òðåíèÿ, îò âèäà è ñâîéñòâ ïîêðûòèé è ñìàçîê, îò âíåøíèõ

óñëîâèé (òåìïåðàòóðû, âèáðàöèé, äàâëåíèÿ è äð.), êðîìå òîãî, îíè äîëæíû

îïèñûâàòü èçìåíåíèÿ èçíîñà âî âðåìåíè [52,55,56].

Áîëüøîå êîëè÷åñòâî ïàðàìåòðîâ, îò êîòîðûõ çàâèñèò èçíàøèâàíèå ìàòåðèàëîâ,

ñëîæíîñòü è ìíîãîîáðàçèå ñîïóòñòâóþùèõ ïðîöåññîâ ïðèâåëî ê òîìó, ÷òî ïðàêòè÷åñêè

íå ñóùåñòâóåò îáùåïðèíÿòûõ çàâèñèìîñòåé, êîòîðûå áû îïèñûâàëè èçíàøèâàíèå ìàòå-

ðèàëîâ èñõîäÿ òîëüêî èç ôèçè÷åñêîé ñóùíîñòè è ôèçèêî-õèìè÷åñêèõ ïàðàìåòðîâ. Äëÿ

ýòîé öåëè, êàê ïðàâèëî, èñïîëüçóþòñÿ ýìïèðè÷åñêèå èëè ïîëóýìïèðè÷åñêèå çàâèñèìî-

ñòè, ñïðàâåäëèâûå äëÿ îïðåäåëåííîãî âèäà èçíàøèâàíèÿ, â îïðåäåëåííûõ óñëîâèÿõ è

äëÿ îïðåäåëåííîãî ñî÷åòàíèÿ ìàòåðèàëîâ [33,56]. Îáùåïðèçíàíî, ÷òî äëÿ öåëåé èíæå-

íåðíûõ ðàñ÷åòîâ íåîáõîäèìî ó÷èòûâàòü âëèÿíèå òðåõ îñíîâíûõ ôàêòîðîâ: ñî÷åòàíèÿ

ìàòåðèàëîâ, êîíñòðóêöèè è ðåæèìîâ ðàáîòû ôðèêöèîííîé ïàðû [55].

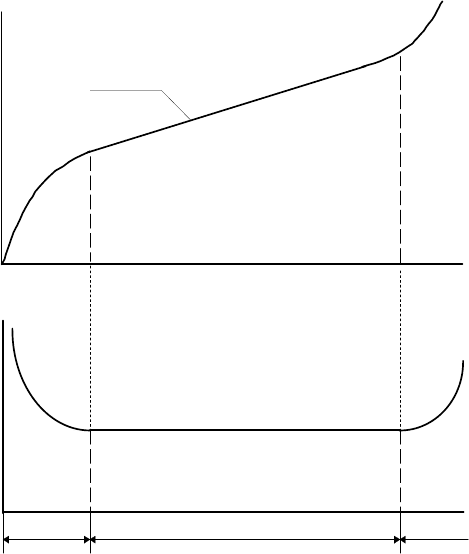
Èçíàøèâàíèå ÿâëÿåòñÿ ìíîãîñòàäèéíûì ïðîöåññîì, ïîýòîìó êðèâûå çàâèñèìîñòè

èçíîñà îò âðåìåíè, êàê ïðàâèëî, ñîñòîÿò èç äâóõ èëè òðåõ ó÷àñòêîâ (ðèñ.3.12). Òèïè÷-

íàÿ êðèâàÿ èçíîñà ñîñòîèò èç òðåõ ó÷àñòêîâ (ðèñ.3.12à) [23]. Â ïåðèîä ïðèðàáîòêè ïðî-

èñõîäèò èçìåíåíèå íà÷àëüíîãî (òåõíîëîãè÷åñêîãî) ðåëüåôà ïîâåðõíîñòè ìàòåðèàëà â

ýêñïëóàòàöèîííûé. Â ýòîò ïåðèîä ñêîðîñòü èçíàøèâàíèÿ (ðèñ.3.12á) óìåíüøàåòñÿ äî

çíà÷åíèÿ g=const, õàðàêòåðíîãî äëÿ ïå-

ðèîäà óñòàíîâèâøåãîñÿ (íîðìàëüíîãî)

èçíîñà. Äëÿ íåêîòîðûõ ñëó÷àåâ õàðàêòå-

ðåí òàêæå ïåðèîä êàòàñòðîôè÷åñêîãî èç-

íîñà ñ èíòåíñèâíûì âîçðàñòàíèåì ñêî-

ðîñòè èçíàøèâàíèÿ. Ýòîò ïåðèîä ñâÿçàí

ñ èçìåíåíèåì âèäà èçíàøèâàíèÿ.

Ïåðèîä ïðèðàáîòêè îáû÷íî ñîñòàâ-

ëÿåò íåñêîëüêî ïðîöåíòîâ îò îáùåãî

âðåìåíè ýêñïëóàòàöèè, à ýêñïëóàòàöèÿ

èçäåëèé â ïåðèîä êàòàñòðîôè÷åñêîãî èç-

íîñà, êàê ïðàâèëî, íå äîïóñêàåòñÿ èëè

íå ðàöèîíàëüíà. Ïîýòîìó ìîæíî ñ÷è-

òàòü, ÷òî äëÿ ïðîöåññîâ èçíàøèâàíèÿ

íàèáîëåå õàðàêòåðíà ëèíåéíàÿ çàâèñè-

ìîñòü h=gt èëè h = h

+gt [38].

Íà çíà÷åíèå ñêîðîñòè èçíàøè-

âàíèÿ îïðåäåëÿþùåå âëèÿíèå îêà-

çûâàþò äàâëåíèå íà ïîâåðõíîñòè

òðåíèÿ p è ñêîðîñòü îòíîñèòåëüíî-

ãî ñêîëüæåíèÿ v. Â îáùåì ñëó÷àå

ñêîðîñòü èçíàøèâàíèÿ ìîæåò áûòü

âûðàæåíà çàâèñèìîñòüþ [53]

g = kp

, (3.45)

ãäå k - êîýôôèöèåíò èçíîñà, õàðàêòåðè-

çóþùèé ìàòåðèàëû ïàðû òðåíèÿ è óñëîâèÿ

èçíàøèâàíèÿ; a = 0,5¸3,0 è b » 1 - ïîêàçà-

òåëè, ó÷èòûâàþùèå âèä èçíàøèâàíèÿ.

1 2 3

const

à)

á)

Ðèñ.3.12. Òèïè÷íûå çàâèñèìîñòè èçíîñà (à)

è ñêîðîñòè èçíàøèâàíèÿ (á) îò âðåìåíè [13]:

1- ïåðèîä ïðèðàáîòêè, 2- ïåðèîä óñòàíîâèâøåãîñÿ

(íîðìàëüíîãî) èçíîñà, 3-

ïåðèîä êàòàñòðîôè÷åñêîãî

èçíîñà

112

Äëÿ ìíîãèõ âèäîâ èçíàøèâàíèÿ (íàïðèìåð, àáðàçèâíîãî [23]) a = b = 1.

Òîãäà

g = kpv, h = h

+ kpvt = h

+ kps, (3.46)

ãäå s = vt - ïóòü òðåíèÿ.

Íà çíà÷åíèå êîýôôèöèåíòà òðåíèÿ k âëèÿþò õàðàêòåðèñòèêè ìàòåðèà-

ëîâ è óñëîâèÿ â çîíå êîíòàêòà (â ïåðâóþ î÷åðåäü - ñìàçêà ïîâåðõíîñòåé).

Çàâèñèìîñòü èíòåíñèâíîñòè èçíàøèâàíèÿ j = h/s = g/v îò ðåæèìà ðàáî-

òû ñîïðÿæåíèÿ è ïðî÷íîñòíûõ õàðàêòåðèñòèê ìîæíî âûðàçèòü â âèäå

, (3.47)

ãäå d è R - ãëóáèíà âíåäðåíèÿ è ðàäèóñ åäèíè÷íîé íåðîâíîñòè; p è p

- íîìèíàëüíîå è

ôàêòè÷åñêîå äàâëåíèÿ; k

- ïîñòîÿííàÿ, õàðàêòåðèçóþùàÿ ðàñïðåäåëåíèå íåðîâíîñòåé

ïî âûñîòå,

kfp

0 0

(3.48)

- ÷èñëî öèêëîâ äî ðàçðóøåíèÿ íåðîâíîñòåé; s - ïðåäåë ïðî÷íîñòè ìàòåðèàëà; f - êîýô-

ôèöèåíò òðåíèÿ; b - ïîêàçàòåëü, çàâèñÿùèé îò ñìàçêè è ìåõàíè÷åñêèõ ñâîéñòâ òðóùèõ-

ñÿ òåë (â óñëîâèÿõ óïðóãîãî êîíòàêòà b = 10¸15).

3.3.8. Эрозионное разрушение материалов

Ïðîöåññû ýðîçèè îáúåäèíÿþò íåñêîëüêî âèäîâ ïîâåðõíîñòíîãî ðàçðó-

øåíèÿ òåëà ïîä âîçäåéñòâèåì äèíàìè÷åñêèõ ïîòîêîâ æèäêîñòåé, ãàçîâ,

òâåðäûõ ÷àñòèö èëè ýëåêòðè÷åñêèõ ðàçðÿäîâ. Â áîëüøèíñòâå ñëó÷àåâ â

ïðîöåññàõ ýðîçèè ïðîèñõîäèò èíòåíñèâíîå ðàçðóøåíèå ìàòåðèàëîâ ñ îáðà-

çîâàíèåì ïèòòèíãîâ, êàâåðí è ðàêîâèí, êîòîðîå ÷àñòî ïðèâîäèò ê ïðåæäå-

âðåìåííîé ïîòåðå ðàáîòîñïîñîáíîñòè ýëåìåíòîâ òåõíè÷åñêèõ ñèñòåì [8].

Àíàëèç ïðîöåññîâ ýðîçèè çàòðóäíÿåòñÿ ìíîãîîáðàçèåì ôèçè÷åñêèõ ìå-

õàíèçìîâ, âûçûâàþùèõ ïîâåðõíîñòíîå ðàçðóøåíèå ìàòåðèàëîâ è èõ ñî÷å-

òàíèé (òàáë.3.3), à òàêæå áîëüøèì êîëè÷åñòâîì ôàêòîðîâ, îêàçûâàþùèõ

âëèÿíèå íà õàðàêòåð è ôîðìû ïðîÿâëåíèÿ ïðîöåññîâ. Êðîìå òîãî, ýðîçèîí-

íîìó ðàçðóøåíèþ ìàòåðèàëîâ ÷àñòî ñîïóòñòâóþò ïðîöåññû, êîñâåííî ñâÿ-

çàííûå ñ íèì è îêàçûâàþùèå íà åãî êèíåòèêó ñóùåñòâåííîå âëèÿíèå (íà-

ïðèìåð, ãàçîâàÿ ýðîçèÿ ÷àñòî ñîïðîâîæäàåòñÿ ïðîöåññàìè õèìè÷åñêîé

êîððîçèè, òåðìè÷åñêîé óñòàëîñòè, öåìåíòàöèè, àçîòèðîâàíèÿ è äð.).

Ïðîöåññû ýðîçèè ðåäêî ïðîòåêàþò ïî îäíîìó ìåõàíèçìó è ýòî çíà÷è-

òåëüíî óñëîæíÿåò êàðòèíó ðàçðóøåíèÿ. Îäíàêî â êàæäîì ñëó÷àå ìîæíî

âûäåëèòü îñíîâíîé ìåõàíèçì, ëèìèòèðóþùèé íàäåæíîñòü ýëåìåíòà.

Ìåõàíîõèìè÷åñêàÿ ýðîçèÿ ïðîÿâëÿåòñÿ, êîãäà ýíåðãèÿ ïîòîêà æèäêî-

ñòè, ãàçà èëè òâåðäûõ ÷àñòèö íåäîñòàòî÷íà äëÿ ïëàñòè÷åñêîé äåôîðìàöèè,

ñòðóêòóðíûõ èëè ôàçîâûõ èçìåíåíèé ìàòåðèàëà íà ãëóáèíå íåñêîëüêèõ

ìèêðîí è ðàçðóøåíèå ïðîèñõîäèò â ïîâåðõíîñòíûõ ñóáìèêðîñêîïè÷åñêèõ

ñëîÿõ â ðåçóëüòàòå ðàçðóøåíèÿ è óíîñà ïëåíîê âòîðè÷íûõ ñòðóêòóð. Èí-

òåíñèâíîñòü ðàçðóøåíèÿ íåçíà÷èòåëüíà ïî ñðàâíåíèþ ñ äðóãèìè âèäàìè

ýðîçèè, îäíàêî ïðè íåïðàâèëüíîì âûáîðå ìàòåðèàëîâ èëè óñëîâèé ýêñ-

ïëóàòàöèè ìåõàíîõèìè÷åñêàÿ ýðîçèÿ ìîæåò ïðèâåñòè ê ïðåæäåâðåìåííîìó

âûõîäó ýëåìåíòà èç ñòðîÿ. Êðîìå òîãî, ñêîðîñòü ýðîçèè ìîæåò áûòü ðàç-

ëè÷íîé íà ðàçëè÷íûõ ó÷àñòêàõ ïîâåðõíîñòè, ÷òî ÷àñòî ïðèâîäèò ê âîçíèê-

113

íîâåíèè âîëí, ëîêàëüíûõ óãëóáëå-

íèé è ðàêîâèí è ìîæåò îòðèöàòåëü-

íî ñêàçàòüñÿ íà íàäåæíîñòè.

Ìèêðîóäàðíàÿ ýðîçèÿ íàáëþäà-

åòñÿ â ñëó÷àÿõ, êîãäà ïîâåðõíîñòü

ìàòåðèàëà â ïîòîêå ãàçà, æèäêîñòè

èëè òâåðäûõ ÷àñòèö ïîäâåðãàåòñÿ

ëîêàëüíûì óäàðàì, ýíåðãèÿ êîòîðûõ

äîñòàòî÷íà äëÿ ïëàñòè÷åñêîé äå-

ôîðìàöèè, ñòðóêòóðíûõ èëè ôàçî-

âûõ ïðåâðàùåíèé. Ìèêðîóäàðíîå

âîçäåéñòâèå ÿâëÿåòñÿ ñëîæíûì âè-

äîì íàãðóæåíèÿ: óäàðíûì, ìíîãî-

êðàòíûì, ëîêàëüíûì, íåðàâíîìåð-

íûì è ìèêðîîáúåìíûì. Îñíîâíîé åãî îñîáåííîñòüþ ÿâëÿåòñÿ ëîêàëèçàöèÿ

îòäåëüíîãî äåôîðìàöèîííîãî àêòà â îáúåìå, ñîèçìåðèìîì ñî ñòðóêòóðíûìè

ñîñòàâëÿþùèìè ìàòåðèàëà (íàïðèìåð, çåðíàìè). Ïðè ýòîì âîçðàñòàåò ðîëü

ãðàíèö ñòðóêòóðíûõ ñîñòàâëÿþùèõ â ïðîöåññå çàðîæäåíèÿ è ðàçâèòèÿ

ìèêðîòðåùèí. Êðîìå òîãî, ñïåöèôèêà âîçäåéñòâèÿ ïðèâîäèò ê ïðîÿâëåíèþ

íåîáû÷íûõ ñâîéñòâ ìàòåðèàëà (íàïðèìåð, ìàðòåíñèò ïðè ìèêðîóäàðíîì

âîçäåéñòâèè ïðîÿâëÿåò âûñîêóþ ïëàñòè÷íîñòü). ×àñòíûì ñëó÷àåì ìèêðî-

óäàðíîé ýðîçèè ÿâëÿåòñÿ ýðîçèÿ ïðè êàâèòàöèè.

Ïðè ìèêðîóäàðíîé ýðîçèè ñíà÷àëà íàáëþäàåòñÿ íåêîòîðûé èíêóáàöèîííûé ïåðèîä,

êîãäà íà ïîâåðõíîñòè ìàòåðèàëà ïðîèñõîäÿò èçìåíåíèÿ ìèêðî- è ñóáìèêðîðåëüåôà è

òðàíñôîðìàöèÿ ñòðóêòóðû â òîíêîì ïîâåðõíîñòíîì ñëîå (â ÷àñòíîñòè ñäâèãè è äðîáëå-

íèÿ çåðåí). Ïðîäîëæèòåëüíîñòü èíêóáàöèîííîãî ïåðèîäà â çàâèñèìîñòè îò ñâîéñòâ ìà-

òåðèàëà è óñëîâèé ïðîöåññà - îò íåñêîëüêèõ ñåêóíä äî íåñêîëüêèõ ñîò ÷àñîâ. Çàòåì èç-

çà âûñîêîé íåîäíîðîäíîñòè ïëàñòè÷åñêîé äåôîðìàöèè â ïîâåðõíîñòíûõ ñëîÿõ ïðîèñõî-

äèò äèñëîêàöèîííîå çàðîæäåíèå è ðàçâèòèå òðåùèí âïëîòü äî îòäåëåíèÿ ÷àñòèö ìàòå-

ðèàëà. Ñêîðîñòü ïðîöåññà çàâèñèò îò ýíåðãèè óäàðà, ïðèðîäû ìàòåðèàëà, åãî ñòðóêòóðû

è ñóáñòðóêòóðû, ñêëîííîñòè ê óïðî÷íåíèþ è ðàçóïðî÷íåíèþ.

Òåðìè÷åñêàÿ ýðîçèÿ ÿâëÿåòñÿ îñíîâíûì ìåõàíèçìîì ïðè âçàèìîäåéñò-

âèè ìàòåðèàëà ñ ðàñêàëåííûì ãàçîâûì ïîòîêîì. Ðàçðóøåíèå ïðîèñõîäèò â

ðåçóëüòàòå òîãî, ÷òî ïîâåðõíîñòü ìàòåðèàëà, íàãðåòàÿ äî âûñîêîé òåìïåðà-

òóðû (èíîãäà âûøå òåìïåðàòóðû ïëàâëåíèÿ), ñëàáî ñîïðîòèâëÿåòñÿ äèíà-

ìè÷åñêîìó âîçäåéñòâèþ ãàçîâîãî ïîòîêà. Ïðè ýòîì ñâÿçè ìåæäó ÷àñòèöàìè

ìàòåðèàëà îñëàáåâàþò è îíè óíîñÿòñÿ ãàçîâûì ïîòîêîì. Îáðàçîâàâøèåñÿ

ïðè ýòîì êàâåðíû â äàëüíåéøåì óñèëèâàþò ýðîçèîííûé ïðîöåññ. Â íåêî-

òîðûõ ñëó÷àÿõ ïðîöåññ òåðìè÷åñêîé ýðîçèè ìîæåò óñèëèâàòüñÿ ñîïóòñò-

âóþùèìè ýôôåêòàìè (ïèðîëèçîì, èñïàðåíèåì, ñóáëèìàöèåé è äð.).

Â çàâèñèìîñòè îò âèäà ìàòåðèàëà è óñëîâèé ïðîöåññà â êàæäîì ñëó÷àå

(ñì.òàáë.3.3) ìîæåò ïðåîáëàäàòü îäèí èç îïèñàííûõ ìåõàíèçìîâ.

Ïðè ãèäðîýðîçèè ïðè îòíîñèòåëüíî íèçêèõ ñêîðîñòÿõ ïîòîêà æèäêîñòè âåäóùèì

ÿâëÿåòñÿ ìåõàíîõèìè÷åñêèé ìåõàíèçì, ïðè âûñîêèõ ñêîðîñòÿõ - ìèêðîóäàðíîå ðàçðó-

øåíèå. Ãèäðîýðîçèîííîìó ðàçðóøåíèþ ÷àñòî ñîïóòñòâóþò ïðîöåññû ýëåêòðîõèìè÷åñêîé

ýðîçèè. Ñèëîâîå âîçäåéñòâèå ìîæåò áûòü âûçâàíî êàê îáû÷íûìè óäàðàìè ìèêðîîáúå-

ìîâ æèäêîñòè, òàê è êàâèòàöèîííûìè ïðîöåññàìè.

Êàâèòàöèÿ - ïðîöåññ îáðàçîâàíèÿ ïàðîãàçîâûõ ïóçûðüêîâ â îãðàíè÷åííîì îáúåìå

æèäêîñòè, ãäå â ðåçóëüòàòå ãèäðîäèíàìè÷åñêèõ ôëóêòóàöèé äàâëåíèå ñòàíîâèòñÿ íèæå

äàâëåíèÿ ïàðîâ æèäêîñòè ïðè äàííîé òåìïåðàòóðå, è èõ ïîñëåäóþùåãî óíè÷òîæåíèÿ

(ñõëîïûâàíèÿ) â çîíå ïîâûøåííîãî äàâëåíèÿ. Â ðåçóëüòàòå êàâèòàöèè âîçíèêàþò ëî-

êàëüíûå ãèäðàâëè÷åñêèå óäàðû áîëüøîé ñèëû (â íåêîòîðûõ ñëó÷àÿõ íà ïëîùàäè 1 ñì

Òàáëèöà 3.3

КЛАССИФИКАЦИЯ ВИДОВ ЭРОЗИИ [8]

Ïðèçíàê

Âèäû ýðîçèè

Ìåõàíèçì

ïðîòåêàíèÿ

ïðîöåññà

Ìåõàíîõèìè÷åñêàÿ

Ìèêðîóäàðíàÿ

Òåðìè÷åñêàÿ

Ýëåêòðè÷åñêàÿ

Õàðàêòåð

ðàñïðåäåëåíèÿ

ïîâðåæäåíèé

Îáùàÿ

Ëîêàëüíàÿ

Óñëîâèÿ

ïðîòåêàíèÿ

ïðîöåññà

Ãèäðîýðîçèÿ

Ãàçîâàÿ

Àáëÿöèÿ

Àáðàçèâíàÿ

Ãèäðîàáðàçèâíàÿ

Ýëåêòðè÷åñêàÿ

114

çà îäíó ñåêóíäó ìîæåò îáðàçîâàòüñÿ è óíè÷òîæèòüñÿ áîëåå 30 ìèëëèîíîâ êàâèòàöèîí-

íûõ ïóçûðüêîâ). Â ðàçâèòèè êàâèòàöèîííîãî ðàçðóøåíèÿ ìàòåðèàëîâ ìîæíî âûäåëèòü

÷åòûðå õàðàêòåðíûõ ïåðèîäà: èíêóáàöèîííûé, â òå÷åíèå êîòîðîãî ðàçðóøåíèå ïðàêòè-

÷åñêè íå íàáëþäàåòñÿ, ïåðèîä íàðàñòàþùåãî ðàçðóøåíèÿ, â òå÷åíèå êîòîðîãî ïðîèñõî-

äèò çàðîæäåíèå êàâåðí, ïåðèîä ðàâíîìåðíîãî ðàçðóøåíèÿ, êîãäà ïðîèñõîäèò äàëüíåé-

øåå ðàçâèòèå êàâåðí ïî âñåé ïîâåðõíîñòè, è ïåðèîä çàòóõàíèÿ ðàçðóøåíèÿ âñëåäñòâèå

çàòðóäíåííîãî äàëüíåéøåãî ðàçâèòèÿ ãëóáîêèõ êàâåðí.

Ãàçîâàÿ ýðîçèÿ ïðîèñõîäèò ïðè êîíòàêòå ïîâåðõíîñòè ìàòåðèàëîâ ñ ãàçîâûì ïîòî-

êîì, â ïåðâóþ î÷åðåäü - ñ âûñîêîòåìïåðàòóðíûìè è õèìè÷åñêè àêòèâíûìè ãàçîâûìè

ñòðóÿìè. Âûñîêîòåìïåðàòóðíîé ãàçîâîé ýðîçèè îáû÷íî ñîïóòñòâóþò ïðîöåññû îêêëþçèè

(îáúåìíîå ïîãëîùåíèå ãàçîâ òâåðäûìè èëè ðàñïëàâëåííûìè ìàòåðèàëàìè), ãàçîâîé

êîððîçèè, òåðìè÷åñêîé óñòàëîñòè, âòîðè÷íîé çàêàëêè è îòïóñêà, öåìåíòàöèè, àçîòèðî-

âàíèÿ è äð.

Àáëÿöèåé íàçûâàåòñÿ ðàçðóøåíèå ïîâåðõíîñòåé íåìåòàëëè÷åñêèõ ìàòåðèàëîâ â ïî-

òîêå ðàñêàëåííûõ ãàçîâ. Ïðîöåññ àáëÿöèè, êàê ïðàâèëî, ñîïðîâîæäàåòñÿ òåðìè÷åñêèìè

ýôôåêòàìè (ïèðîëèçîì, èñïàðåíèåì, ñóáëèìàöèåé è ò.ä.).

Àáðàçèâíàÿ ýðîçèÿ âîçíèêàåò ïðè ïîâåðõíîñòíîì ðàçðóøåíèè ìàòåðèàëîâ ïîä äåé-

ñòâèåì òâåðäûõ ÷àñòèö â ïîòîêå æèäêîñòåé èëè ãàçîâ (ãèäðî- è ãàçîàáðàçèâíàÿ ýðîçèÿ).

Ãëàâíûìè ôàêòîðàìè, îïðåäåëÿþùèìè ñèëîâîå âîçäåéñòâèå íà ïîâåðõíîñòü ìàòåðèàëà,

ÿâëÿþòñÿ òâåðäîñòü, ïðî÷íîñòü, ðàçìåð è ôîðìà ÷àñòèö, à òàêæå îñîáåííîñòè èõ äâè-

æåíèÿ âáëèçè ïîâåðõíîñòè (ñêîðîñòü, óãîë àòàêè è äð.). Çàêîíîìåðíîñòè ïîâåðõíîñòíî-

ãî ðàçðóøåíèÿ ñóùåñòâåííî çàâèñÿò îò ñîñòàâà ñðåäû è åå õèìè÷åñêîé àêòèâíîñòè.

Îáùèå êèíåìàòè÷åñêèå çàêîíîìåðíîñòè ïðîöåññà àáðàçèâíîé ýðîçèè áëèçêè ê çàêîíî-

ìåðíîñòÿì ãèäðîýðîçèè. Ïðè îòíîñèòåëüíî íèçêèõ ñêîðîñòÿõ ÷àñòèö è, ñîîòâåòñòâåííî,

íåáîëüøèõ çíà÷åíèÿõ ýíåðãèè óäàðà ðàçðóøåíèå ëîêàëèçóåòñÿ â òîí÷àéøèõ ïîâåðõíî-

ñòíûõ ñëîÿõ âòîðè÷íûõ ñòðóêòóð è ïðîòåêàåò ïðåèìóùåñòâåííî ïî ìåõàíîõèìè÷åñêîìó

ìåõàíèçìó. Ïðè íåêîòîðîé êðèòè÷åñêîé ýíåðãèè óäàðà äåôîðìàöèîííûå ïðîöåññû íà-

÷èíàþò ðàçâèâàòüñÿ â áîëåå ãëóáîêèõ ñëîÿõ ìàòåðèàëà, âåäóùèì ñòàíîâèòñÿ ìèêðî-

óäàðíîå ðàçðóøåíèå, èíòåíñèâíîñòü ýðîçèè ðåçêî óâåëè÷èâàåòñÿ, ðàçðóøåíèå äîñòèãàåò

îñíîâíîãî ìàòåðèàëà.

Ãèäðîàáðàçèâíàÿ ýðîçèÿ ïðè êàâèòàöèè íàáëþäàåòñÿ ïðè îäíîâðåìåííîì âîçäåé-

ñòâèè íà ìàòåðèàë äèíàìè÷åñêèõ ïîòîêîâ æèäêîñòè, àáðàçèâíûõ ÷àñòèö è ëîêàëüíûõ

êàâèòàöèîííûõ ãèäðîóäàðîâ.

3.4. Процессы теплового разрушения

Òåïëîâàÿ óñòîé÷èâîñòü òâåðäûõ òåë, êàê è ìåõàíè÷åñêàÿ ïðî÷íîñòü,

îïðåäåëÿåòñÿ ýíåðãèåé ìåæìîëåêóëÿðíîé èëè ìåæàòîìíîé ñâÿçè (ýíåðãèåé

êðèñòàëëè÷åñêîé ðåøåòêè). Áîëüøàÿ âåëè÷èíà ýíåðãèè ñâÿçè îïðåäåëÿåò

ñïîñîáíîñòü ìàòåðèàëà ê îáðàçîâàíèþ êðèñòàëëè÷åñêèõ ðåøåòîê ñ âûñîêîé

òåïëîñòîéêîñòüþ, ìåõàíè÷åñêîé è ýëåêòðè÷åñêîé ïðî÷íîñòüþ.

Â çàâèñèìîñòè îò ñêîðîñòè íàãðåâà ìàòåðèàë ïëàâèòñÿ èëè èñïàðÿåòñÿ:

ìåäëåííîå íàãðåâàíèå ñîïðîâîæäàåòñÿ ïëàâëåíèåì è èñïàðåíèåì ðàñïëàâà,

áûñòðîå íàãðåâàíèå âûçûâàåò èñïàðåíèå (ñóáëèìàöèþ) òâåðäîãî òåëà.

3.4.1. Плавление твердых материалов

Ïðîöåññ ïëàâëåíèÿ õàðàêòåðèçóåòñÿ òåìïåðàòóðîé è òåïëîòîé ïëàâëå-

íèÿ (êîëè÷åñòâîì ýíåðãèè, íåîáõîäèìûì äëÿ ïëàâëåíèÿ îäíîãî ìîëÿ âåùå-

ñòâà ïðè ïîñòîÿííîé òåìïåðàòóðå). ×åì âûøå ýíåðãèÿ ìåæàòîìíûõ èëè

ìåæìîëåêóëÿðíûõ ñâÿçåé, òåì âûøå òåìïåðàòóðà ïëàâëåíèÿ è áîëüøå òå-

ïëîòà ïëàâëåíèÿ. Ñâÿçü ìåæäó òåìïåðàòóðîé ïëàâëåíèÿ, òåïëîòîé ïëàâëå-

íèÿ è èçìåíåíèåì îáúåìà âûðàæàåòñÿ óðàâíåíèåì Êëàïåéðîíà-Êëàóçèóñà

E T V

ïë ïë

ïë

= D , (3.49)

ãäå E

ïë

- òåïëîòà ïëàâëåíèÿ; T

ïë

- òåìïåðàòóðà ïëàâëåíèÿ; P - äàâëåíèå; DV - èçìåíå-

íèå îáúåìà ïðè ïëàâëåíèè.

115

Ïðèðîäà ôèçè÷åñêèõ ïðîöåññîâ, ïðîèñõîäÿùèõ ïðè ìåõàíè÷åñêîì è òå-

ïëîâîì ðàçðóøåíèè ìàòåðèàëîâ, î÷åíü áëèçêà. Â ÷àñòíîñòè, îäíîâðåìåí-

íîå äåéñòâèå ìåõàíè÷åñêîé íàãðóçêè è íàãðåâàíèÿ îêàçûâàåò îäèíàêîâîå

ñîâîêóïíîå äåéñòâèå, óñêîðÿþùåå ðàçðóøåíèå.

Ïëàâëåíèå ñîïðîâîæäàåòñÿ çíà÷èòåëüíûìè èçìåíåíèÿìè ôèçè÷åñêèõ

ñâîéñòâ ìàòåðèàëîâ: óâåëè÷åíèåì ýíòðîïèè, ðîñòîì òåïëîåìêîñòè è ýëåê-

òðè÷åñêîãî ñîïðîòèâëåíèÿ (çà èñêëþ÷åíèåì íåêîòîðûõ ïîëóïðîâîäíèêîâ),

ïðàêòè÷åñêè äî íóëÿ ïàäàåò ñîïðîòèâëåíèå ñäâèãó, óìåíüøàåòñÿ ñêîðîñòü

ðàñïðîñòðàíåíèÿ çâóêà è ò.ä. Ïîýòîìó ñîçäàíèå óñëîâèé äëÿ íà÷àëà ïðî-

öåññà ïëàâëåíèÿ, êàê ïðàâèëî, îçíà÷àåò îòêàç ýëåìåíòà.

Ñîãëàñíî ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè, ïëàâëåíèå òâåðäûõ ìàòåðèàëîâ ïðè

íàãðåâå è, ñîîòâåòñòâåííî, óâåëè÷åíèè ýíåðãèè è àìïëèòóäû êîëåáàíèé àòîìîâ íà÷èíà-

åòñÿ ñ óâåëè÷åíèÿ â êðèñòàëëå êîëè÷åñòâà ðàçëè÷íûõ äåôåêòîâ (â ïåðâóþ î÷åðåäü - âà-

êàíñèé). Â ìîëåêóëÿðíûõ êðèñòàëëàõ îäíîâðåìåííî ìîæåò ïðîèñõîäèòü ÷àñòè÷íîå ðà-

çóïîðÿäî÷åíèå âçàèìíîé îðèåíòàöèè ìîëåêóë. Ïîñòåïåííûé ðîñò ÷èñëà äåôåêòîâ è èõ

îáúåäèíåíèå ñ ïîâûøåíèåì òåìïåðàòóðû õàðàêòåðèçóþò ñòàäèþ ïðåäïëàâëåíèÿ. Ñ äîñ-

òèæåíèåì òåìïåðàòóðû ïëàâëåíèÿ â êðèñòàëëå ñîçäàåòñÿ êðèòè÷åñêàÿ êîíöåíòðàöèÿ

äåôåêòîâ è íà÷èíàåòñÿ ñîáñòâåííî ïëàâëåíèå - êðèñòàëëè÷åñêàÿ ðåøåòêà ðàñïàäàåòñÿ

íà ëåãêîïîäâèæíûå ñóáìèêðîñêîïè÷åñêèå ôðàãìåíòû. Ïîäâîäèìàÿ ïðè ýòîì ýíåðãèÿ

èäåò íå íà íàãðåâ, à íà ðàçðûâ ìåæàòîìíûõ ñâÿçåé è ðàçðóøåíèå äàëüíåãî ïîðÿäêà â

êðèñòàëëàõ, ïîýòîìó íà ýòîé ñòàäèè òåìïåðàòóðà íå ìåíÿåòñÿ. Â ñàìèõ æå ñóáìèêðî-

ñêîïè÷åñêèõ ôðàãìåíòàõ áëèæíèé ïîðÿäîê â ðàñïîëîæåíèè àòîìîâ ñóùåñòâåííî íå ìå-

íÿåòñÿ (ïîýòîìó ñâîéñòâà, çàâèñÿùèå îò äàëüíåãî ïîðÿäêà, ïðè ïëàâëåíèè ìåíÿþòñÿ

ñèëüíî, à ñâîéñòâà, çàâèñÿùèå îò áëèæíåãî ïîðÿäêà,- ñëàáî).

Íàëè÷èå îïðåäåëåííîé òåìïåðàòóðû ïëàâëåíèÿ - âàæíûé îòëè÷èòåëü-

íûé ïðèçíàê êðèñòàëëè÷åñêîãî ñòðîåíèÿ òåë (àìîðôíûå òåëà íå èìåþò

ôèêñèðîâàííîé òåìïåðàòóðû ïëàâëåíèÿ, îíè ïåðåõîäÿò â æèäêîå ñîñòîÿ-

íèå ïîñòåïåííî ðàçìÿã÷àÿñü).

Çàâèñèìîñòü òåìïåðàòóðû ïëàâëåíèÿ îò ïðèðîäû êðèñòàëëè÷åñêîãî âåùåñòâà âûðà-

æàåòñÿ ýìïèðè÷åñêîé ôîðìóëîé Ëèíäåìàíà

ïë

= BMV

2/3

, (3.50)

ãäå B - ïîñòîÿííàÿ; çàâèñÿùàÿ îò ñòðóêòóðû êðèñòàëëà; M - ìîëåêóëÿðíàÿ ìàññà; V -

ìîëåêóëÿðíûé îáúåì; t

- äåáàåâñêàÿ òåìïåðàòóðà.

Ïðèìåñè ñíèæàþò òåìïåðàòóðó ïëàâëåíèÿ. Ïëàâëåíèå ñïëàâîâ è òâåð-

äûõ ðàñòâîðîâ ïðîèñõîäèò, êàê ïðàâèëî, â îïðåäåëåííîì èíòåðâàëå òåìïå-

ðàòóð, êîòîðûé çàâèñèò îò ñîñòàâà (ñîäåðæàíèÿ êîìïîíåíòîâ). Ó íåêîòî-

ðûõ âûñîêîìîëåêóëÿðíûõ ñîåäèíåíèé (íàïðèìåð, âåùåñòâ, ñïîñîáíûõ îá-

ðàçîâûâàòü æèäêèå êðèñòàëëû) ïåðåõîä èç òâåðäîãî êðèñòàëëè÷åñêîãî ñî-

ñòîÿíèÿ â èçîòðîïíîå æèäêîå ïðîèñõîäèò ïîñòàäèéíî (êàæäàÿ ñòàäèÿ õà-

ðàêòåðèçóåò îïðåäåëåííûé ýòàï ðàçðóøåíèÿ êðèñòàëëè÷åñêîé ñòðóêòóðû).

3.4.2. Сублимация (испарение) твердых материалов

Ïðîöåññ ñóáëèìàöèè òâåðäûõ ìàòåðèàëîâ (ïåðåõîä âåùåñòâà èç êðèñòàë-

ëè÷åñêîãî ñîñòîÿíèÿ íåïîñðåäñòâåííî â ãàçîîáðàçíîå áåç ïëàâëåíèÿ) âîç-

ìîæåí âî âñåì èíòåðâàëå òåìïåðàòóð è äàâëåíèé, ïðè êîòîðûõ òâåðäàÿ è

ãàçîîáðàçíàÿ ôàçû ñîñóùåñòâóþò. Ñóáëèìàöèÿ ìåòàëëè÷åñêèõ êðèñòàëëîâ

ïðèâîäèò ê îáðàçîâàíèþ îäíîàòîìíûõ ïàðîâ, èîííûå êðèñòàëëû îáðàçóþò â

ãàçîâîé ôàçå ïîëÿðíûå ìîëåêóëû, ìîëåêóëÿðíûå êðèñòàëëû îáðàçóþò ïàðû,

ñîñòîÿùèå èç ìîëåêóë. Ïðîöåññû ñóáëèìàöèè èìåþò îñîáåííî áîëüøîå

ïðàêòè÷åñêîå çíà÷åíèå ïðè íåêîòîðûõ óñëîâèÿõ ýêñïëóàòàöèè. Â óñëîâèÿõ

ãëóáîêîãî âàêóóìà (íàïðèìåð, â êîñìîñå) ñóáëèìàöèÿ ìàòåðèàëîâ îêàçûâàåò

íåïîñðåäñòâåííîå âëèÿíèå íà ðàáîòîñïîñîáíîñòü òåõíè÷åñêèõ îáúåêòîâ.

116

Èñïàðåíèå òâåðäîãî ìàòåðèàëà ïðîèñõîäèò â ðåçóëüòàòå óâåëè÷åíèÿ

ýíåðãèè òåïëîâîãî äâèæåíèÿ äî âåëè÷èíû ýíåðãèè ñóáëèìàöèè, íåîáõîäè-

ìîé äëÿ ïðåîäîëåíèÿ ñèë ñâÿçè ìåæäó ÷àñòèöàìè è èõ îòðûâà ñ ïîâåðõíî-

ñòè êðèñòàëëà. Ïðè èñïàðåíèè òâåðäîãî òåëà êðèñòàëëè÷åñêàÿ ðåøåòêà

ïîëíîñòüþ ðàçðóøàåòñÿ.

Ñêîðîñòü èñïàðåíèÿ ëþáûõ òâåðäûõ òåë â âàêóóìå

n = n

exp(–E

/RT), (3.51)

ãäå E

- òåïëîòà ñóáëèìàöèè (ýíåðãèÿ àêòèâàöèè ïðîöåññà èñïàðåíèÿ îäíîãî ìîëÿ).

Òåïëîòà ñóáëèìàöèè ìîæåò áûòü îïðåäåëåíà èç óðàâíåíèÿ Êëàïåéðîíà-

Êëàóçèóñà (3.49)

(

)

E RT

d P

, (3.52)

ãäå P - äàâëåíèå ïàðà âåùåñòâà ïðè òåìïåðàòóðå T.

Ïðè íå î÷åíü ãëóáîêîì âàêóóìå ñêîðîñòü ñóáëèìàöèè ìåíüøå ðàñ÷åò-

íîé, òàê êàê ÷àñòü ìîëåêóë, ñòàëêèâàÿñü ñ ìîëåêóëàìè âîçäóõà (èëè äðóãî-

ãî ãàçà), âîçâðàùàåòñÿ ê ïîâåðõíîñòè ìàòåðèàëà. Ñêîðîñòü ñóáëèìàöèè ëå-

òó÷åãî êîìïîíåíòà èç ñïëàâà óìåíüøàåòñÿ ïî ñðàâíåíèþ ñî ñêîðîñòüþ

ñóáëèìàöèè ÷èñòîãî ìåòàëëà ïðèìåðíî ïðîïîðöèîíàëüíî åãî êîíöåíòðàöèè.

Ïðè òåðìè÷åñêîì ðàçðóøåíèè (èñïàðåíèè) â âàêóóìå ÷èñòûõ ìåòàëëîâ,

ñïëàâîâ, îêèñëîâ ìåòàëëîâ, äèýëåêòðèêîâ, ïîëóïðîâîäíèêîâ è äðóãèõ âå-

ùåñòâ íàáëþäàþòñÿ çàêîíîìåðíîñòè, àíàëîãè÷íûå ìåõàíè÷åñêîìó ðàçðó-

øåíèþ: òåìïåðàòóðíî-âðåìåííûå çàâèñèìîñòè äëÿ ìåõàíè÷åñêîé è òåïëî-

âîé ïðî÷íîñòè âûðàæàþòñÿ àíàëîãè÷íûìè ýêñïîíåíöèàëüíûìè óðàâíåíèÿ-

ìè, ñ ïîâûøåíèåì òåìïåðàòóðû ýíåðãèÿ àêòèâàöèè ïðîöåññà èñïàðåíèÿ

ñíèæàåòñÿ è ñêîðîñòü èñïàðåíèÿ ðàñòåò.

Íåêîòîðûå ìàòåðèàëû, ïðèìåíÿåìûå äëÿ ïîêðûòèé (íàïðèìåð, êàäìèé è öèíê), â

âàêóóìå ïðè òåìïåðàòóðàõ âûøå 120-180

Ñ ìîãóò èñïàðÿòüñÿ ñ äîâîëüíî çíà÷èòåëüíû-

ìè ñêîðîñòÿìè (ïîðÿäêà 1 ìì/ãîä), ÷òî çàñòàâëÿåò ó÷èòûâàòü ïðîöåññ ñóáëèìàöèè ïðè

ðàñ÷åòå äîëãîâå÷íîñòè ýëåìåíòîâ.

3.5. Процессы электрического разрушения

Ïðîöåññû ýëåêòðè÷åñêîãî ðàçðóøåíèÿ òâåðäûõ äèýëåêòðèêîâ è ïîëó-

ïðîâîäíèêîâ ìîãóò áûòü äâóõ âèäîâ [9,11,57]: ïðîáîé òîëùè ìàòåðèàëà è

ðàçðÿä ïî ïîâåðõíîñòè.

3.5.1. Электрический пробой диэлектриков

Ïðîáîé äèýëåêòðèêà ïðîèñõîäèò ïðè íàëîæåíèè ýëåêòðè÷åñêîãî ïîëÿ,

íàïðÿæåííîñòü êîòîðîãî ïðåâûøàåò êðèòè÷åñêîå çíà÷åíèå - ïðîáèâíóþ

íàïðÿæåííîñòü, õàðàêòåðèçóþùóþ ýëåêòðè÷åñêóþ ïðî÷íîñòü ìàòåðèàëà.

Äëÿ òâåðäûõ äèýëåêòðèêîâ õàðàêòåðíû äâå ôîðìû ïðîáîÿ: ïðîáîé, âûçâàí-

íûé ýëåêòðè÷åñêèì ðàçðÿäîì (÷èñòî ýëåêòðè÷åñêèé ïðîáîé), è òåïëîâîé

ïðîáîé. Â îáëàñòè íèçêèõ òåìïåðàòóð ïðè ÷èñòî ýëåêòðè÷åñêîì ïðîáîå,

ïðîáèâíàÿ íàïðÿæåííîñòü íå çàâèñèò îò òåìïåðàòóðû è ïðàêòè÷åñêè íå

çàâèñèò îò âðåìåíè âîçäåéñòâèÿ. Â îáëàñòè áîëåå âûñîêèõ òåìïåðàòóð íà-

áëþäàåòñÿ òåïëîâîé ïðîáîé è ïðîáèâíàÿ íàïðÿæåííîñòü çàâèñèò îò òåìïå-

ðàòóðû è äëèòåëüíîñòè âîçäåéñòâèÿ (÷åì ìåíüøå âðåìÿ âîçäåéñòâèÿ, òåì

âûøå ïðîáèâíàÿ íàïðÿæåííîñòü).

117

Îáû÷íûå çíà÷åíèÿ íàïðÿæåííîñòè ïðè ýëåêòðè÷åñêîì ïðîáîå ëåæàò â èíòåðâàëå

¸10

Â/ñì, ïðè òåïëîâîì ïðîáîå - 10

¸10

Â/ñì [58]. Äëèòåëüíîñòü âîçäåéñòâèÿ

íàïðÿæåíèÿ äî ïðîáîÿ äëÿ ÷èñòî ýëåêòðè÷åñêîãî ïðîáîÿ ñîñòàâëÿåò îò 10

-8

äî 10 ñ, äëÿ

òåïëîâîãî - îò 0,1 äî 10

ñ [59].

Èíîãäà êàê îòäåëüíûå ôîðìû âûäåëÿþòñÿ õèìè÷åñêèé (ýëåêòðîõèìè÷åñêèé) ïðîáîé

è ïðîáîé, âûçûâàåìûé ôèçè÷åñêèìè äåôåêòàìè äèýëåêòðèêà (ïîðàìè, òðåùèíàìè, ïî-

ñòîðîííèìè âêëþ÷åíèÿìè). Ïîä õèìè÷åñêèì ïðîáîåì ïîíèìàåòñÿ ñíèæåíèå ýëåêòðè÷å-

ñêîé ïðî÷íîñòè âñëåäñòâèå õèìè÷åñêèõ ïðîöåññîâ, ïðîèñõîäÿùèõ â äèýëåêòðèêå ïðè

äëèòåëüíîì âîçäåéñòâèè âûñîêîãî íàïðÿæåíèÿ. Ïðè ýòîì ïîñëåäîâàòåëüíî ïðîèñõîäÿò

äâà ïðîöåññà: ñòàðåíèå äèýëåêòðèêà, ñíèæàþùåå åãî ýëåêòðè÷åñêóþ ïðî÷íîñòü, è ñîá-

ñòâåííî ïðîáîé (òåïëîâîé èëè ýëåêòðè÷åñêèé), ïðè÷åì ïðè äëèòåëüíîé ýêñïëóàòàöèè

ïðîöåññ ñòàðåíèÿ ìîæåò èìåòü ðåøàþùåå çíà÷åíèå äëÿ íàäåæíîñòè.

Ýëåêòðè÷åñêèé ïðîáîé äèýëåêòðèêîâ - ñëîæíûé êîìïëåêñ ýëåêòðè÷å-

ñêèõ, ìåõàíè÷åñêèõ è òåïëîâûõ ïðîöåññîâ è ÿâëåíèé. Ýëåêòðè÷åñêèé ïðî-

áîé â ÷èñòîì âèäå âîçíèêàåò ïðè êðàòêîâðåìåííîì ïðèëîæåíèè íàïðÿæå-

íèÿ â äîñòàòî÷íî îäíîðîäíîì ïîëå â îòñóòñòâèå êðàåâûõ ðàçðÿäîâ. Åãî îò-

ëè÷èòåëüíîé îñîáåííîñòüþ ÿâëÿåòñÿ óâåëè÷åíèå ñèëû òîêà ïåðåä ïðîáîåì

ñ óâåëè÷åíèåì íàïðÿæåíèÿ ïðèáëèçèòåëüíî ïî ýêñïîíåíöèàëüíîìó çàêîíó

è ðåçêîå óâåëè÷åíèå ñèëû òîêà ïðè äîñòèæåíèè ïðîáèâíîãî íàïðÿæåíèÿ.

Âûäåëÿþùàÿñÿ ïðè ýòîì ýíåðãèÿ ñïîñîáíà ðàñïëàâèòü, îáóãëèòü èëè ñæå÷ü

äèýëåêòðèê, ïðè íåáîëüøîì òîêå â ìåñòå ïðîáîÿ îñòàåòñÿ ñëåä â âèäå ïðî-

êîëà èëè ïðîðûâà.

Íàèáîëåå âåðîÿòíûì ìåõàíèçìîì ýëåêòðè÷åñêîãî ïðîáîÿ òâåðäûõ äè-

ýëåêòðèêîâ ÿâëÿåòñÿ óäàðíàÿ èîíèçàöèÿ ýëåêòðîíàìè èëè èîíàìè: ïðè äâè-

æåíèè â êðèñòàëëè÷åñêîé ðåøåòêå òâåðäîãî òåëà ýëåêòðîíû ïðîâîäèìîñòè

îòäàþò ýíåðãèþ àòîìàì èëè èîíàì êðèñòàëëà, âûçûâàÿ èõ èîíèçàöèþ, ïðè

ïðîáèâíîé íàïðÿæåííîñòè ïîëÿ óäàðíàÿ èîíèçàöèÿ ïðèâîäèò ê ðåçêîìó

óâåëè÷åíèþ êîíöåíòðàöèè íîñèòåëåé â çîíå ïðîâîäèìîñòè. Â ïîðàõ è ãà-

çîâûõ âêëþ÷åíèÿõ äèýëåêòðèêà ïðè äîñòàòî÷íî âûñîêèõ íàïðÿæåíèÿõ, ïðå-

âûøàþùèõ íàïðÿæåíèå èîíèçàöèè, âîçíèêàþò ýëåêòðè÷åñêèå ðàçðÿäû, â

ðåçóëüòàòå êîòîðûõ òàêæå ñîçäàþòñÿ óñëîâèÿ äëÿ ïðîáîÿ äèýëåêòðèêà.

Â ïðîöåññå ïðîáîÿ îáû÷íî ìîæíî âûäåëèòü òðè îñíîâíûõ ñòàäèè: ñòà-

äèþ ôîðìèðîâàíèÿ ðàçðÿäà (ñòàäèþ ëàâèíû), â êîíöå êîòîðîé â ìàòåðèàëå

ñîçäàåòñÿ ïðîâîäÿùèé ïóòü è íàáëþäàåòñÿ ðåçêîå âîçðàñòàíèå ýëåêòðîïðî-

âîäèìîñòè, ñòàäèþ çàâåðøåíèÿ ðàçðÿäà (ñòàäèþ ðàçðóøåíèÿ ìàòåðèàëà),

êîãäà íàïðÿæåíèå íà äèýëåêòðèêå ïàäàåò ïî÷òè äî íóëÿ, è ïîñëåïðîáîé-

íóþ ñòàäèþ, â êîòîðîé òîê îïðåäåëÿåòñÿ â îñíîâíîì ïàðàìåòðàìè ðàçðÿä-

íîãî êîíòóðà.

Âåðîÿòíîñòü îáðàçîâàíèÿ â äèýëåêòðèêå ýëåêòðîííîé ëàâèíû ñ ÷èñëîì ýëåêòðîíîâ,

íåîáõîäèìûì äëÿ ïðîáîÿ, îïðåäåëÿåòñÿ âûðàæåíèåì [11,58,60]

p = n

exp(–n

ïð

ñð

), (3.53)

ãäå n

- íà÷àëüíîå ÷èñëî ñâîáîäíûõ ýëåêòðîíîâ â äèýëåêòðèêå; n

ïð

- ÷èñëî ýëåêòðîíîâ,

íåîáõîäèìîå äëÿ ïðîáîÿ; n

ñð

=exp(d/l

) - ñðåäíèé ðàçìåð ýëåêòðîííîé ëàâèíû; d -

òîëùèíà äèýëåêòðèêà; l

- ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà ìåæäó ñòîëêíîâåíèÿìè.

Ñ óâåëè÷åíèåì íàïðÿæåííîñòè ýëåêòðè÷åñêîãî ïîëÿ èëè òîëùèíû äèýëåêòðèêà âå-

ðîÿòíîñòü p ïðèáëèæàåòñÿ ê åäèíèöå.

Çíà÷åíèå ïðîáèâíîé íàïðÿæåííîñòè ýëåêòðè÷åñêîãî ïîëÿ ìîæíî ïðè-

áëèæåííî îïðåäåëèòü èç óñëîâèÿ ðàâåíñòâà ýíåðãèè, ïåðåäàâàåìîé ýëåê-

òðîíàìè ðåøåòêå, è ñàìîé ýíåðãèè ðåøåòêè [60]:

, (3.54)

118

ãäå a - êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè, ó÷èòûâàþùèé êîëè÷åñòâî ýíåðãèè, ïåðåäàí-

íîé îò ýëåêòðîíà ðåøåòêå, è êîëè÷åñòâî ýëåêòðîíîâ, âçàèìîäåéñòâóþùèõ ñ íåé äî ðàç-

ðóøåíèÿ; m è q - ìàññà è çàðÿä ýëåêòðîíîâ; t

- ñðåäíåå âðåìÿ ñâîáîäíîãî ïðîáåãà

ýëåêòðîíîâ; U - ýíåðãèÿ ðåøåòêè.

Íà ñàìîì äåëå ïðîáèâíàÿ íàïðÿæåííîñòü ïîëÿ E

ïð

çàâèñèò îò áîëüøîãî ÷èñëà êîí-

ñòðóêòèâíûõ è òåõíîëîãè÷åñêèõ ôàêòîðîâ è âíåøíèõ óñëîâèé è ÿâëÿåòñÿ ïî ñóòè ñëó-

÷àéíîé âåëè÷èíîé [61]. Ýëåêòðè÷åñêàÿ ïðî÷íîñòü òåõíè÷åñêèõ äèýëåêòðèêîâ (èçîëÿöè-

îííûõ ìàòåðèàëîâ) â çíà÷èòåëüíîé ñòåïåíè îïðåäåëÿåòñÿ íàëè÷èåì â äèýëåêòðèêå ñëó-

÷àéíî ðàñïðåäåëåííûõ ïî âåëè÷èíå è ïîëîæåíèþ çàãðÿçíÿþùèõ ÷àñòèö, ïðèìåñåé, ãà-

çîâûõ âêëþ÷åíèé è äåôåêòîâ, óñèëèâàþùèõ íåðàâíîìåðíîñòü ýëåêòðè÷åñêîãî ïîëÿ è

ñîçäàþùèõ ñëàáûå ìåñòà â èçîëÿöèè. Â ñâÿçè ñ ýòèì äëÿ îöåíêè ïðîáèâíîé íàïðÿæåí-

íîñòè ýëåêòðè÷åñêîãî ïîëÿ èñïîëüçóþòñÿ âåðîÿòíîñòíûå è ñòàòèñòè÷åñêèå ìåòîäû.

Âðåìÿ ðàçðÿäà ïðè ïðîáîå ñêëàäûâàåòñÿ èç âðåìåíè çàïàçäûâàíèÿ îò ìîìåíòà ïðè-

ëîæåíèÿ íàïðÿæåíèÿ äî ìîìåíòà ïîÿâëåíèÿ "ýôôåêòèâíîãî" ýëåêòðîíà è âðåìåíè ôîð-

ìèðîâàíèÿ ëàâèíû. Ñðåäíåå âðåìÿ ñòàòèñòè÷åñêîãî çàïàçäûâàíèÿ îïðåäåëÿåòñÿ èñõîäÿ

èç ôîðìóëû (3.53) [58]

ñò

= exp(–n

ïð

ñð

)/n

. (3.55)

Ðàçëè÷àþòñÿ äâà îñíîâíûõ âèäà ýëåêòðè÷åñêîãî ðàçðÿäà ïî ïîâåðõíîñòè äèýëåêòðè-

êà è ñîîòâåòñòâóþùåãî èì ýëåêòðè÷åñêîãî ïîâðåæäåíèÿ [11]: ïîâåðõíîñòíîå (äóãîâîå)

ïåðåêðûòèå, ïðè êîòîðîì ýëåêòðè÷åñêàÿ äóãà ïðîèñõîäèò, â îñíîâíîì, â ãàçå íàä ïî-

âåðõíîñòüþ ìàòåðèàëà; ïðîãðåññèðóþùåå ïîâåðõíîñòíîå ïîâðåæäåíèå, êîòîðîå ïðî-

èñõîäèò ïîä âëèÿíèåì ïîâåðõíîñòíûõ äóãîâûõ ðàçðÿäîâ èëè èñêðåíèè, ïðè êàæäîì ðàç-

ðÿäå íà ïîâåðõíîñòè ïîÿâëÿåòñÿ äåôåêò (ïðîâîäÿùèé ñëåä èëè äîðîæêà) ñ ñèëüíîé ýðî-

çèåé ïîâåðõíîñòè. Ýòî ðàçãðàíè÷åíèå íå âñåãäà ÷åòêî âûðàæåíî, äóãîâûå ïåðåêðûòèÿ

ìîãóò âûçâàòü ïðîãðåññèðóþùåå ðàçðóøåíèå è íàîáîðîò.

Âëèÿíèå äóãè è ïðîâîäÿùåãî ñëåäà ÿâëÿåòñÿ â îñíîâíîì òåðìè÷åñêèì - îíè âûçû-

âàþò âûñîêîòåìïåðàòóðíûå ðåàêöèè (ðàçëîæåíèå, ãîðåíèå). Â ñëó÷àå îáðàçîâàíèÿ ïðî-

âîäÿùåãî ñëåäà ïîâðåæäàþùèå ðàçðÿäû îáû÷íî ñîïðîâîæäàþòñÿ ìåíüøèìè òîêàìè, âû-

çûâàþòñÿ è ïîääåðæèâàþòñÿ íàëè÷èåì âëàãè èëè çàãðÿçíåíèé. Ïðè äóãîâîì ïåðåêðûòèè

âëàãà íå âëèÿåò íà âîçíèêíîâåíèå ðàçðÿäà.

Ìíîãèå îñîáåííîñòè, îòíîñÿùèåñÿ ê ýëåêòðè÷åñêîìó ïðîáîþ, òàêæå õàðàêòåðèçóþò

è ïîâåðõíîñòíîå ýëåêòðè÷åñêîå ïîâðåæäåíèå. Äóãîâîå ïåðåêðûòèå èçîëÿöèîííûõ ìàòå-

ðèàëîâ çàâèñèò îò áîëüøîãî ÷èñëà ôàêòîðîâ: ïëîùàäè è ñîñòîÿíèÿ ïîâåðõíîñòè, åå

ðàñïîëîæåíèÿ îòíîñèòåëüíî ýëåêòðîäîâ, äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè äèýëåêòðèêà

è ñðåäû, ýëåêòðè÷åñêîé ïðî÷íîñòè ñðåäû, ôîðìû è ïðîäîëæèòåëüíîñòè äåéñòâèÿ íà-

ïðÿæåíèÿ, òîëùèíû èçîëÿöèè, èçîëÿöèîííûõ ðàññòîÿíèé è äð. Áîëüøîå êîëè÷åñòâî

ôàêòîðîâ îïðåäåëÿåò â îñíîâíîì ýìïèðè÷åñêèé ïîäõîä ê ïðîãíîçèðîâàíèþ âåðîÿòíîñòè

âîçíèêíîâåíèÿ ïîâåðõíîñòíîãî ðàçðÿäà è âûáîðà èçîëÿòîðîâ.

Òåïëîâîé ïðîáîé ïðîèñõîäèò ïðè äëèòåëüíîì âîçäåéñòâèè íàïðÿæåíèÿ

è ÿâëÿåòñÿ ñëåäñòâèåì íàðóøåíèÿ òåïëîâîãî ðàâíîâåñèÿ äèýëåêòðèêà, êî-

ãäà ïîäâîä òåïëà ïðåâûøàåò îòâîä ïóòåì òåïëîïðîâîäíîñòè, èçëó÷åíèÿ è

êîíâåêöèè [62]. Â ðåçóëüòàòå êàòàñòðîôè÷åñêîãî íàðàñòàíèÿ êîëè÷åñòâà

âûäåëÿåìîãî òåïëà ïðîèñõîäèò òåðìè÷åñêîå ðàçðóøåíèå ìàòåðèàëà (ïðî-

æèãàíèå, ïëàâëåíèå èëè ðàçëîæåíèå). Ïðîáîé âîçíèêàåò â ñëó÷àå, êîãäà

ïðèëîæåííîå íàïðÿæåíèå íåäîñòàòî÷íî äëÿ ÷èñòî ýëåêòðè÷åñêîãî ïðîáîÿ

(ïðè íà÷àëüíîé òåìïåðàòóðå) è âñëåäñòâèå âûäåëåíèÿ òåïëà ïðîèñõîäèò

òàêîå ïîâûøåíèå òåìïåðàòóðû, ÷òî ýëåêòðè÷åñêàÿ ïðî÷íîñòü ñíèæàåòñÿ

äî âåëè÷èíû, ñîîòâåòñòâóþùåé ïðèëîæåííîìó íàïðÿæåíèþ. Âîçìîæíîñòü

ðàçâèòèÿ òåïëîâîãî ïðîáîÿ îáóñëîâëåíà òåì, ÷òî ïðîâîäèìîñòü äèýëåêòðè-

êà âîçðàñòàåò ñ ïîâûøåíèåì òåìïåðàòóðû ïî ýêñïîíåíöèàëüíîìó çàêîíó.

3.5.2. Электрический пробой полупроводников

Ïîëóïðîâîäíèêè, êàê è äèýëåêòðèêè, îáëàäàþò îïðåäåëåííîé ýëåêòðè-

÷åñêîé ïðî÷íîñòüþ, êîòîðàÿ õàðàêòåðèçóåòñÿ ïðîáèâíîé íàïðÿæåííîñòüþ

ýëåêòðè÷åñêîãî ïîëÿ. Ðàçëè÷èÿ ìåæäó äèýëåêòðèêàìè è ïîëóïðîâîäíèêàìè

çàêëþ÷àþòñÿ, ãëàâíûì îáðàçîì, â øèðèíå ïîëîñû çàïðåùåííûõ ýíåðãèé

119

ìåæäó âàëåíòíîé çîíîé è çîíîé ïðîâîäèìîñòè: â äèýëåêòðèêàõ îíà áîëüøå

3 ýÂ, â ïîëóïðîâîäíèêàõ - ìåíüøå 2 ýÂ [9].

Ïîòåðÿ ýëåêòðè÷åñêîé ïðî÷íîñòè è ïðîáîé ïîëóïðîâîäíèêîâ ïîä äåéñò-

âèåì ýëåêòðè÷åñêîãî ïîëÿ â çàâèñèìîñòè îò óñëîâèé ìîæåò áûòü âûçâàí

ðàçëè÷íûìè ôèçè÷åñêèìè ïðîöåññàìè. Â ñâÿçè ñ ýòèì ðàçëè÷àþòñÿ ÷èñòî

ýëåêòðè÷åñêèé, òåïëîâîé è êîìáèíèðîâàííûé ìåõàíèçìû ïðîáîÿ.

Âîçíèêíîâåíèå ÷èñòî ýëåêòðè÷åñêîãî ïðîáîÿ ïîëóïðîâîäíèêîâûõ ìà-

òåðèàëîâ â ñèëüíîì ýëåêòðè÷åñêîì ïîëå îáóñëîâëåíî ðåçêèì óâåëè÷åíèåì

êîíöåíòðàöèè íîñèòåëåé çàðÿäà âñëåäñòâèå ãåíåðàöèè ýëåêòðîííî-

äûðî÷íûõ ïàð ýëåêòðè÷åñêèì ïîëåì. Â ïîëóïðîâîäíèêàõ ñ óâåëè÷åíèåì

îáðàòíîãî íàïðÿæåíèÿ, ïðèëîæåííîãî ê ýëåêòðîííî-äûðî÷íîìó (p-n) ïåðå-

õîäó, ïðè äîñòèæåíèè íåêîòîðîãî íàïðÿæåíèÿ ïðîèñõîäèò ðåçêîå âîçðàñ-

òàíèå îáðàòíîãî òîêà è âîçíèêàåò ïðîáîé p-n-ïåðåõîäà.

Ðàçëè÷àþòñÿ äâà îñíîâíûõ ìåõàíèçìà ýëåêòðè÷åñêîãî ïðîáîÿ â îáúåìå ïîëóïðîâîä-

íèêîâ: ýëåêòðîñòàòè÷åñêèé èëè òóííåëüíûé ïðîáîé, âûçûâàåìûé ýëåêòðîñòàòè÷å-

ñêîé èîíèçàöèåé, è óäàðíûé èëè ëàâèííûé ïðîáîé, âûçûâàåìûé óäàðíîé èîíèçàöèåé

[62]. Ïðîáîé ìîæåò íàñòóïèòü è â ðåçóëüòàòå ñîâìåñòíîãî äåéñòâèÿ óäàðíîé è ýëåêòðî-

ñòàòè÷åñêîé èîíèçàöèè. Íàðÿäó ñ ïðîáîåì â îáúåìå â ïîëóïðîâîäíèêå ìîæåò íàáëþ-

äàòüñÿ òàêæå ïîâåðõíîñòíûé ïðîáîé. Ýëåêòðîñòàòè÷åñêàÿ èîíèçàöèÿ îáóñëîâëåíà âîç-

ìîæíîñòüþ âûðûâàíèÿ ýëåêòðîíîâ è èõ ïîñëåäóþùåãî ïðÿìîãî ïåðåõîäà èç âàëåíòíîé

çîíû â ñâîáîäíóþ â ñèëüíîì ýëåêòðè÷åñêîì ïîëå (òóííåëüíûé ýôôåêò). Ñ óâåëè÷åíèåì

øèðèíû p-n-ïåðåõîäà íàïðÿæåííîñòü ïîëÿ â ïåðåõîäå ïàäàåò è ýëåêòðîñòàòè÷åñêèé

(òóííåëüíûé) ïðîáîé ñòàíîâèòñÿ íåâîçìîæíûì.

Íàèáîëåå âåðîÿòíûì ìåõàíèçìîì ýëåêòðè÷åñêîãî ïðîáîÿ ïîëóïðîâîäíèêîâ (êàê è

äèýëåêòðèêîâ) ÿâëÿåòñÿ óäàðíàÿ èîíèçàöèÿ ýëåêòðîíàìè, ïðèîáðåòàþùèìè â äîñòàòî÷-

íî ñèëüíîì ýëåêòðè÷åñêîì ïîëå íåîáõîäèìóþ êèíåòè÷åñêóþ ýíåðãèþ âî âðåìÿ ñâîáîä-

íûõ ïðîáåãîâ ìåæäó ñòîëêíîâåíèÿìè. Áûñòðûå íîñèòåëè çàðÿäà ñòàëêèâàþòñÿ ñ àòîìà-

ìè ðåøåòêè êðèñòàëëà è èîíèçèðóþò èõ, îòäàâàÿ ýíåðãèþ. Ïðè ýòîì îáðàçóþòñÿ ïàðû

ýëåêòðîí-äûðêà, êîòîðûå òàêæå óñêîðÿþòñÿ ïîëåì è â ñâîþ î÷åðåäü îáðàçóþò íîâûå

ïàðû. Òàêèì îáðàçîì ïðîèñõîäèò ëàâèíîîáðàçíîå ðàçìíîæåíèå íîñèòåëåé çàðÿäà [62].

Ïðîöåññ ëàâèííîãî óìíîæåíèÿ íîñèòåëåé çàðÿäà, âûçûâàþùèé åãî ýëåêòðè÷åñêèé

ïðîáîé è îáóñëîâëåííûé óäàðíîé èîíèçàöèåé, îáû÷íî õàðàêòåðèçóåòñÿ êîýôôèöèåíòîì

óìíîæåíèÿ M

, ðàâíûì îòíîøåíèþ êîíå÷íîãî ÷èñëà ýëåêòðîíîâ n ê ÷èñëó ýëåêòðîíîâ

, ââîäèìûõ â ð-n-ïåðåõîä [63,64]. Íàïðÿæåíèå ïðîáîÿ çàâèñèò îò óäåëüíîãî ñîïðî-

òèâëåíèÿ è òèïà ïðîâîäèìîñòè ïîëóïðîâîäíèêà [64-66]. Çàâèñèìîñòè íàïðÿæåíèÿ ýëåê-

òðè÷åñêîãî ïðîáîÿ äëÿ êîíêðåòíûõ òèïîâ ïîëóïðîâîäíèêîâûõ ýëåìåíòîâ îïðåäåëÿþòñÿ

òàêæå ñõåìîé èõ âêëþ÷åíèÿ è ðåæèìîì ðàáîòû [63,66].

Íàðÿäó ñ îáúåìíûì ïðîáîåì p-n-ïåðåõîäà â ïîëóïðîâîäíèêîâûõ ýëåìåíòàõ ìîæåò

íàáëþäàòüñÿ ïîâåðõíîñòíûé ïðîáîé, ñâÿçàííûé ñ âëèÿíèåì ïîâåðõíîñòíîãî çàðÿäà íà

íàïðÿæåííîñòü ýëåêòðè÷åñêîãî ïîëÿ è øèðèíó ïåðåõîäà. Ïîâåðõíîñòíûé ïðîáîé, êàê è

îáúåìíûé, ÿâëÿåòñÿ ëàâèíîîáðàçíûì ïðîöåññîì, ìåõàíèçì êîòîðîãî ñâÿçàí ñ ðàñïðåäå-

ëåíèåì ýëåêòðîñòàòè÷åñêîãî ïîòåíöèàëà âáëèçè ïîâåðõíîñòè. Â öåëîì íàïðÿæåíèå ïî-

âåðõíîñòíîãî ïðîáîÿ ìåíüøå îáúåìíîãî â íåñêîëüêî ðàç è çàâèñèò â ïåðâóþ î÷åðåäü îò

äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè ñðåäû, íàëè÷èÿ âëàãè è çàãðÿçíåíèé íà ïîâåðõíîñòè

ïîëóïðîâîäíèêà.

Ïðè óâåëè÷åíèè îáðàòíîãî íàïðÿæåíèÿ, ïðèëîæåííîãî ê p-n-ïåðåõîäó ïîëóïðîâîä-

íèêîâîãî ýëåìåíòà, ðàññåèâàåìàÿ ìîùíîñòü óâåëè÷èâàåòñÿ. Ýòî ïðèâîäèò ê óâåëè÷åíèþ

òåìïåðàòóðû, ÷òî â ñâîþ î÷åðåäü âûçûâàåò ïîâûøåíèå îáðàòíîãî òîêà è ðàññåèâàåìîé

ìîùíîñòè. Ïðè íåäîñòàòî÷íîé èíòåíñèâíîñòè òåïëîîòäà÷è â îêðóæàþùóþ ñðåäó ýëå-

ìåíò íå óñïåâàåò îõëàäèòüñÿ, ïðîèñõîäèò ëàâèíîîáðàçíîå óâåëè÷åíèå òåìïåðàòóðû è

òåïëîâîé ïðîáîé, êîòîðûé, êàê ïðàâèëî, ñîïðîâîæäàåòñÿ ðàçðóøåíèåì ïåðåõîäà.

Óñëîâèåì íîðìàëüíîé ðàáîòû ïîëóïðîâîäíèêîâîãî ýëåìåíòà ÿâëÿåòñÿ

óñòàíîâëåíèå ñòàöèîíàðíîé òåìïåðàòóðû, ïðè êîòîðîé âûäåëÿþùàÿñÿ

ýíåðãèÿ ðàâíà ýíåðãèè, îòâîäèìîé â îêðóæàþùóþ ñðåäó çà ñ÷åò òåïëîîò-

äà÷è. Êðîìå òîãî, íåîáõîäèìî, ÷òîáû ïðè ïðåêðàùåíèè äåéñòâèÿ äîïóñ-

êàåìûõ âíåøíèõ ñëó÷àéíûõ âîçìóùåíèé (ïîâûøåíèè òåìïåðàòóðû, ïè-

òàþùåãî íàïðÿæåíèÿ è ò.ä.) èëè ïðè äîïóñêàåìîì èçìåíåíèè ïàðàìåòðîâ

120

ñàìîãî ýëåìåíòà, âûçâàâøåì óâåëè÷åíèå âûäåëÿåìîé ýíåðãèè, âíîâü óñòà-

íàâëèâàëàñü ñòàöèîíàðíàÿ òåìïåðàòóðà, ò.å. ÷òîáû ñòàöèîíàðíîå ñîñòîÿíèå

íå áûëî íåîáðàòèìî íàðóøåíî.

3.6. Процессы старения материалов

Ñòàðåíèåì ìàòåðèàëîâ íàçûâàþòñÿ ïðîöåññû èçìåíåíèÿ èõ ñâîéñòâ âî

âðåìåíè â óñëîâèÿõ äëèòåëüíîé ýêñïëóàòàöèè èëè õðàíåíèÿ. Îáû÷íî ñòà-

ðåíèå îáóñëîâëåíî íåäîñòàòî÷íî ñòàáèëüíûì èëè íåðàâíîâåñíûì ñîñòîÿ-

íèåì ìàòåðèàëà è åãî ïîñòåïåííûì ïåðåõîäîì â ñòàáèëüíîå èëè ðàâíîâåñ-

íîå ñîñòîÿíèå. Ýòîò ïåðåõîä ìîæåò áûòü ñâÿçàí ñî ñòðóêòóðíûìè ïðåâðà-

ùåíèÿìè èëè ðåëàêñàöèîííûìè ïðîöåññàìè.

Ëþáîé ïðîöåññ ñòàðåíèÿ âîçíèêàåò è ðàçâèâàåòñÿ òîëüêî ïðè îïðåäå-

ëåííûõ âíåøíèõ óñëîâèÿõ. Äëÿ îöåíêè âîçìîæíûõ èçìåíåíèé ìàòåðèàëîâ

íåîáõîäèìî óñòàíîâèòü óñëîâèÿ âîçíèêíîâåíèÿ è îáëàñòü ñóùåñòâîâàíèÿ

ïðîöåññà ñòàðåíèÿ.

Â îáùåì ñëó÷àå ïðè ñòàðåíèè ìîæåò ïðîèñõîäèòü êàê óõóäøåíèå, òàê è óëó÷øåíèå

ñâîéñòâ ìàòåðèàëîâ, ÷àñòî óëó÷øåíèå îäíèõ ñâîéñòâ ñîïðîâîæäàåòñÿ óõóäøåíèåì äðó-

ãèõ. Èíîãäà äëÿ óëó÷øåíèÿ èëè ñòàáèëèçàöèè íåêîòîðûõ õàðàêòåðèñòèê ìàòåðèàëîâ

ïðèìåíÿþòñÿ ìåòîäû èñêóññòâåííîãî ñòàðåíèÿ.

3.6.1. Старение металлов и сплавов

Ìåòàëëè÷åñêèå ñïëàâû ìîãóò ïðåäñòàâëÿòü ñîáîé õèìè÷åñêèå ñîåäèíå-

íèÿ, òâåðäûå ðàñòâîðû âíåäðåíèÿ èëè çàìåùåíèÿ è ìåòàëëè÷åñêèå ñîåäè-

íåíèÿ, ÿâëÿþùèåñÿ ïðîìåæóòî÷íîé ôàçîé ìåæäó õèìè÷åñêèìè ñîåäèíå-

íèÿìè è òâåðäûìè ðàñòâîðàìè.

Ïðîöåññû ñòàðåíèÿ â ìåòàëëàõ è ñïëàâàõ ìîãóò áûòü ñâÿçàíû ñ àëëî-

òðîïè÷åñêèì èëè ìàðòåíñèòíûì ïðåâðàùåíèåì, óïîðÿäî÷åíèåì è ðàçóïî-

ðÿäî÷åíèåì òâåðäûõ ðàñòâîðîâ, ðàñïàäîì ìàðòåíñèòíîé ñòðóêòóðû, ðàñòâî-

ðåíèåì â òâåðäîì ñîñòîÿíèè, ðàñïàäîì ïåðåñûùåííûõ òâåðäûõ ðàñòâîðîâ,

îáðàçîâàíèåì òâåðäîãî ðàñòâîðà èç ýâòåêòîèäíîé ñìåñè è ýâòåêòîèäíûì

ðàñïàäîì [31]. Âñå âèäû ïðåâðàùåíèé ìîãóò áûòü ðàçäåëåíû íà äâå áîëü-

øèå ãðóïïû [11]: ïðîöåññû, ñâÿçàííûå ñ èçìåíåíèåì êðèñòàëëè÷åñêîé

ñòðóêòóðû (áåç èçìåíåíèÿ õèìè÷åñêîãî ñîñòàâà), è ïðîöåññû, ñâÿçàííûå ñ

îáðàçîâàíèåì ôàç è èçìåíåíèåì õèìè÷åñêîãî ñîñòàâà. Íåêîòîðûå ïðîöåñ-

ñû ìîãóò ïðîèñõîäèòü â øèðîêîì äèàïàçîíå òåìïåðàòóð, äðóãèå - òîëüêî

ïðè îïðåäåëåííûõ (èíîãäà î÷åíü âûñîêèõ èëè î÷åíü íèçêèõ) òåìïåðàòóðàõ.

Íàèáîëüøåå ïðàêòè÷åñêîå çíà÷åíèå äëÿ ìåòàëëîâ è ìåòàëëè÷åñêèõ

ñïëàâîâ èìåþò ïðîöåññû ñòàðåíèÿ, ñâÿçàííûå ñ ðàñïàäîì ïåðåñûùåííûõ

òâåðäûõ ðàñòâîðîâ (ïðîöåññû âûäåëåíèÿ) è ðàñïàäîì ìàðòåíñèòíîé ñòðóê-

òóðû [11]. Ýòè ïðîöåññû îáóñëîâëåíû íåóñòîé÷èâîé (ìåòàñòàáèëüíîé)

ñòðóêòóðîé ñïëàâà, îáðàçóþùåéñÿ ïðè òåõíîëîãè÷åñêîé îáðàáîòêå (çàêàë-

êå, íàêëåïå è äð.) è ñâÿçàííîé ñ ïîÿâëåíèåì èñêàæåíèé êðèñòàëëè÷åñêîé

ðåøåòêè èëè îáðàçîâàíèåì êðèñòàëëè÷åñêîé ñòðóêòóðû, íå ñâîéñòâåííîé

ñïëàâó ïðè äàííîé òåìïåðàòóðå. Òàêîå ìåòàñòàáèëüíîå ñîñòîÿíèå õàðàêòå-

ðèçóåòñÿ ïîâûøåííûì óðîâíåì âíóòðåííåé ñâîáîäíîé ýíåðãèè, è ñóùíîñòü

ïðîöåññà ñòàðåíèÿ çàêëþ÷àåòñÿ â ñàìîïðîèçâîëüíîì ïåðåõîäå èõ ìåòàñòà-

áèëüíîãî ñîñòîÿíèÿ â ñòàáèëüíîå ñ áîëåå íèçêèì óðîâíåì âíóòðåííåé

ýíåðãèè, ñâÿçàííûì ñ ïåðåìåùåíèÿìè àòîìîâ â êðèñòàëëè÷åñêîé ðåøåòêå.