Новотный Л., Хехт Б. Основы нанооптики
Подождите немного. Документ загружается.


14.2.
Излучение
флуктуирующих
источников
413
поля
в
w""
тогда
как
второе
обусловлено
магнитным
полем.
Вообще,
п,.",
можно
записать
в
следующей
форме:
w
'"
(г,
"-J)
=
w("-J,
T)N(r,
"-J),
(1448)
где
W("-J,T)
-
средняя
энергия
в
расчете
на
моду.
N(r,"-J)
зависит
только
от
диэлектрических
свойств
€("-J)
и
функции
Грина
системы
отсчета
и
имеет
смысл
определенной
ранее
локальной
плотности
состояний.
Фактически,
и
это
будет
показано
в
дальнейшем,
N(r,
"-J)
идентична
локальной
плотности
состояний,
если
си
стема
находится
в
состоянии
равновесия.
В
неравновесной
системе
N(r,"-J)
включает
в
себя
лишь
часть
полного
числа
возможных
мод.
14.2.1.
ИЗJlучение
аБСОJlЮТНО
черного
TeJla.
Рассмотрим
тело,
состоящее
из
флуктуирующих
точечных
источников.
Термодинамическое
равновесие
с
излучением
проявляется
в
том,
что
усредненный
вектор
Пойнтинга
равен
нулю
во
всех
точ
ках
г
пространства
(отсутствует
перенос
тепла).
В
этом
случае
можно
применить
флуктуационно-диссипационную
теорему
(14.32).
В
свободном
пространстве
два
слагаемых
в
(14.47)
становятся
равны,
и
мы
получаем
[10]
W",(r,
"-J)
=
[1
_
en:::''''/kT]
1Г:
2
L
1т
{[Б(г,
г,
"-J)]n}
(в
равновесии).
(14.49)
J
Полная
энергия
дается
интегрированием
по
положительным
и
отрицательным
часто
там.
Заменим
выражение
в
квадратных
скобках
симметричной
и
антисимметричной
частями:
[]
n;
+
~
+
e""'/~~
_ 1 . (14.50)
....
Принимая
во
внимание
то
обстоятельство,
что
Im(G) -
нечетная
функция
ш,
опустим
первое
слагаемое
в
приведенном
выше
выражении,
поскольку
после
интегри
рования
по
всем частотам
его
вклад
оказывается
равным
нулю.
Оставшийся
интеграл
можно
взять,
проводя
интегрирование
только
по
положительным
частотам:
где
х
00
W = J
W+
",("-J)duJ
= J
W("-J,
T)N(r,
"-J)duJ,
о о
W("-J,
Т)
=
[n;
+
eli",/~~
_
1]
,
N(r,"-J) =
2~
L
lm
{[G(r,r,"-J)]JJ} =
2~
тr
{[G(r,r,"-J)]}
1ГС
.
1ГС
J
(14.51)
совпадает
с
локальной
плотностью
состояний
(ср.
(8.117»,
а
W("-J,
Т)
соответствует
-+
средней
энергии
квантового
осциллятора.
W
",("-J)
-
спектральная
плотность
энер-
гии,
определенная
только
на
множестве
положительных
частот
.
....
Раскладывая
экспоненциальный
множитель
ехр(
ikr)
в
G
в
ряд,
как
это
было
....
пока
за
но
в
разд.
8.3.3,
можно
убедиться,
что
Im(G)
не
является
сингулярной
в
начале
координат.
Используя
функцию
Грина
в
свободном
пространстве.
получаем
1т
{[G(r,r,"-J)]JJ} =
"-J/(6nc),
и
равенство
(14.51)
принимает
вид
-+
( [
1iы
nu;
] u;2
W'"
"-J)
=
2""
+
exp(1iыjkT)
_ 1
~.
(14.52)
414
Гл
14.
Взаимодействия,
обусловленные
флуктуациями
ох
[мкм]
10
1 2
u)
(1014
C-
I
)
5
-+
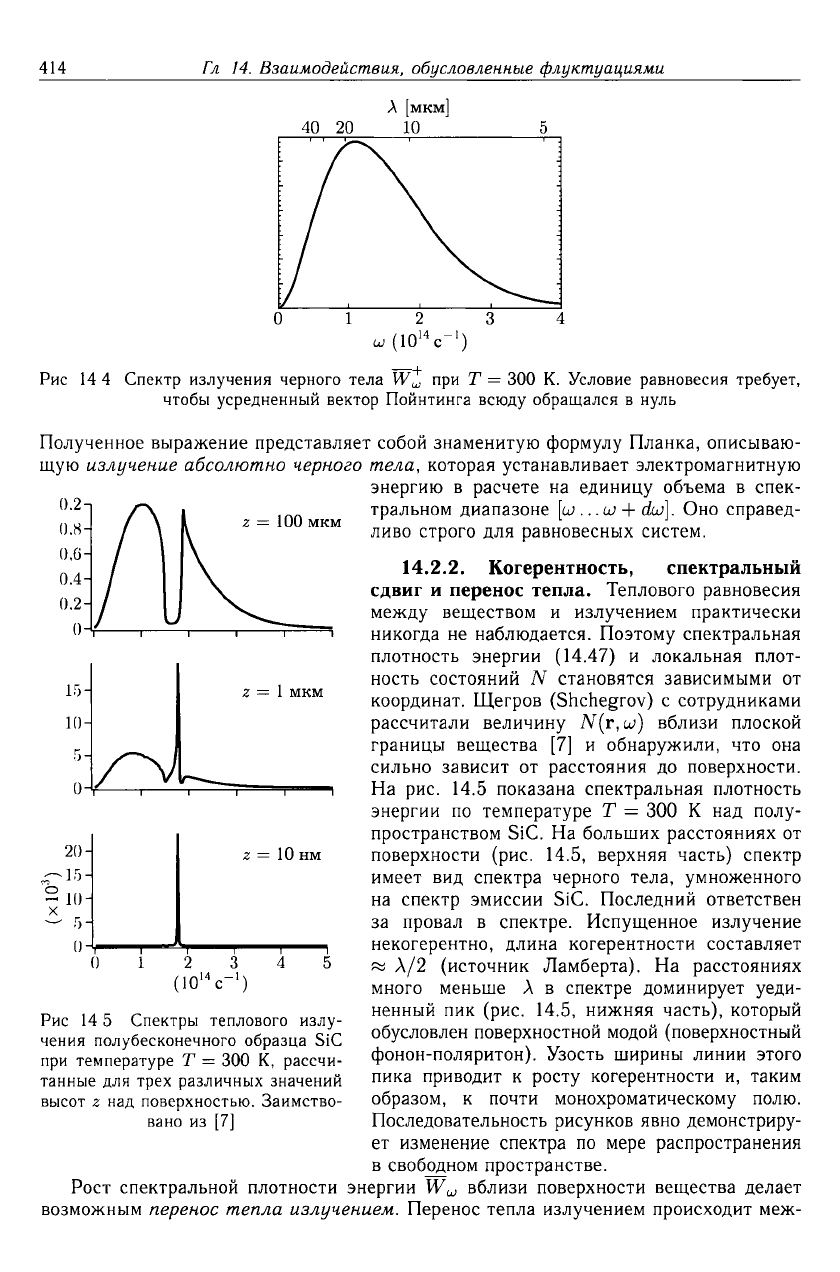
Рис
144
Спектр
излучения
черного
тела
W"'
при
Т
= 300
К.
Условие
равновесия
требует,
чтобы
усредненный
вектор
Пойнтинга
всюду
обращался
в
нуль
Полученное
выражение
представляет
собой
знаменитую
формулу
Планка,
описываю
щую
излучение
абсолютно
черного
тела,
которая
устанавливает
электромагнитную
энергию
в
расчете
на
единицу
объема
в
спек-
0.2
тральном
диапазоне
[c.v
...
c.v
+
dc.v].
Оно
справед-
z =
1ООмкм
О.Н
ливо
строго
для
равновесных
систем.
0,6
0.4
0.2
О
~-"'--':::::"'---,---==::;:=""""'I
z=IMKM
10
z =
IOнм
Рис
14
5
Спектры
теплового
излу
чения
полубесконечного
образца
SiC
при
температуре
Т
= 300
К,
рассчи-
танные
для
трех
различных
значений
высот
z
над
поверхностью.
Заимство
вано
из
[7]
14.2.2.
Когерентность,
спектраJlЬНЫЙ
сдвиг
и
перенос
теПJlа.
Теплового
равновесия
между
веществом
и
излучением
практически
никогда
не
наблюдается.
Поэтому
спектральная
плотность
энергии
(14.47)
и
локальная
плот
ность
состояний
N
становятся
зависимыми
от
координат.
Щегров
(Shchegrov)
с
сотрудниками
рассчитали
величину
N(r,
c.v)
вблизи
плоской
границы
вещества
[7]
и
обнаружили,
что она
сильно
зависит
от
расстояния
до
поверхности.
На
рис.
14.5
показана
спектральная
плотность
энергии
по
температуре
Т
= 300
К
над
полу
пространством
SiC.
На
больших
расстояниях
от
поверхности
(рис.
14.5,
верхняя
часть)
спектр
имеет
вид
спектра
черного
тела,
умноженного
на
спектр
эмиссии
SiC.
Последний
ответствен
за
провал
в
спектре.
Испущенное
излучение
некогерентно,
длина
когерентности
составляет
~
>"/2
(источник
Ламберта).
На
расстояниях
много
меньше
>..
в
спектре
доминирует
уеди
ненный
пик
(рис.
14.5,
нижняя
часть),
который
обусловлен
поверхностной
модой
(поверхностный
фонон-поляритон).
Узость
ширины
линии
этого
пика приводит
к
росту
когерентности
и,
таким
образом,
к
почти
монохроматическому
полю.
Последовательность
рисунков
явно
демонстриру-
ет
изменение
спектра
по
мере
распространения
в
свободном
пространстве.
Рост
спектральной
плотности
энергии
Иf~
вблизи
поверхности
вещества
делает
возможным
перенос
тепла
излучением.
Перенос
тепла
излучением
происходит
меж-

14.3.
Флукmуационно-индуцированные
силы
415
ду
двумя
телами
с
разными
температурами.
Однако
даже
одно
тело
в
свободном
пространстве
теряет
энергию
путем
непрерывного
излучения.
Муле
(Mulet)
с
сотруд
никами
показал,
что
теплоперенос
излучением
между
двумя
телами
можно
увеличить
на
несколько
порядков,
уменьшая
расстояние
между
телами
[11].
Этот
рост
обусловлен
взаимодействием
поверхностных
волн,
локализованных
вблизи
границ
раздела.
Взаи
модействие усиливает
перенос
тепла,
ограниченный
узким
спектральным
окном.
Тепловые
ближние
поля
влияют
не
только
на
спектральную
плотность
энергии
испущенного
излучения,
но
и на
его
nространственную
когерентность.
Мера
пространственной
когерентности
дается
кросс-спектральным
тензором
плотности
электрического
поля
WJk,
который
определяется
следующим
образом:
WJk(rl,
Г2,
UJ)8(UJ
-
UJ')
=
(8E
j
(r
1
'
UJ)8E'k(r2,
UJ'))
.
(1453)
Карминати
(Carminati)
и
Греффе
(Greffet)
вычислили
~jk
вблизи
поверхностей
различных
материалов
[12].
Они
обнаружили,
что
непрозрачные
вещества,
не
поддер
живающие
поверхностные
моды
(например,
вольфрам),
обладают
длиной
простран
ственной
когерентности,
много
меньшей, чем
хорошо
известная
длина
когерентности
излучения
черного
тела
(Лj2).
Длина
когерентности
может
быть
сколь
угодно
малой,
будучи
ограниченной
нелокальными
эффектами
вблизи
поверхности
вещества.
С
дру
гой
стороны,
вблизи
поверхности
материалов,
поддерживающих
поверхностные
моды
(например,
серебро),
длина
когерентности
может
достигать
нескольких
десятков
Л.
14.3.
Флуктуационно-индуцированные
силы
Флуктуирующие
заряды
нейтрального
тела
порождают
флуктуации
электромаг
нитного
поля,
которое
взаимодействует
с
зарядами
других
тел.
Следовательно,
элек
тромагнитное
поле
является
посредником
между
флуктуациями
зарядов
в
отдельных
телах.
Результирующие
корреляции
зарядов
порождают
электромагнитную
силу,
которую
называют
дисперсионной.
При
малых
расстояниях
между
двумя
телами
говорят
о
силе
Ван-дер-Ваальса,
тогда
как
при
больших
расстояниях
говорят
о
си
ле
Казимира.
Хотя
эти
силы
малы
на
макроскопических
масштабах,
ими
нельзя
пренебречь
на
масштабе
наноструктур.
Например,
две
параллельные
проводящие
пластинки
площадью
1
мкм
2
каждая,
расположенные
на
расстоянии
5
нм
друг
от
друга,
будут
притягиваться
с
силой
~
2
нН.
Этой
силы
достаточно,
чтобы
раздавить
биомолекулу!
Дисперсионные силы
ответственны
также
за
слабые
молекулярные
связи
и
за
адгезию
частиц
к
границам
раздела.
Например,
геккон
с
легкостью
взбирается
по
большинству
гладких
поверхностей
и
может
висеть
на
стекле,
держась
одним
пальцем.
Секрет
этих
необычайных
способностей
заключается
в
миллионах
кератиновых
волосков
на
поверхности
каждой
лапки
геккона.
Хотя
связанные
с
каж
дым
волоском
дисперсионные
силы
и
ничтожны,
миллионы
волосков
в
совокупности
порождают
значительную
силу
сцепления.
«Эффект
гeKKOHa~
применен
в
разработке
сильно
клейких
лент.
В
настоящем
разделе,
следуя
[5],
выведем
выражение
для
сил,
действующих
на
малые
поляризуемые
частицы
в
произвольном
окружении.
Для
простоты
записи
предположим,
что
среднее
значение
всех
флуктуаций
равно
нулю;
это
позволяет
записать
равенства
JL(t)
=
8JL(t)
и
E(t)
=
8E(t).
Чтобы
рассчи
тать
силу,
действующую
на
поляризуемую
частицу,
расположенную
в
точке
г
=
го,
используем
выражение
для
градиентной
силы,
полученное
в
разд.
13.3
(см
(13.31».
Однако
следует
учесть,
что
и
поле
Е,
и
ДИПОЛЬНЫЙ
момент
JL
имеют
флуктуационную
и
индуцированную
составляющие.
Поэтому
(F(ro))
= L
[(JL~in)(t)VE;fl)(ro,t))
+
(JL~fl)(t)VE;in)(ro,t))],
(1454)
l

416
Гл
14.
Взаимодействия,
обусловленные
флуктуациями
где
'1.
=
{а:,
у,
z}.
Первое
слагаемое
описывает
флуктуации
поля
(спонтанные
и
теп
ловые),
которые
коррелируют
с
индуцированным
дипольным
моментом
согласно
равенству
ji(in)«(U)
=
Q\«(U)E(fI)(ro,(U),
(14.55)
где
предполагается.
что
поляризуемость
изотропна.
Для
дальнейших
целей
обо
значим
свойства
частицы
индексом
1.
Второе
слагаемое
в
(14.54)
проистекает
из
флуктуаций
дипольного
момента
частицы
и
соответствует
индуцированному
полю
согласно
равенству
2 1
+-+
~('
) W
(П)
Е
tn
(r,(U)
=
2-G(г,го;(U)·ji
«(U).
с
са
(
14.56)
Здесь
G -
функция
Грина
рассматривающейся
системы,
а
r -
произвольная
точка,
как
показано
на
рис.
14.6.
Корреляции
между
флуктуирующим
полем
и
флуктуирую-
Ql(W)
_
(F)
_8
___
G
-.;..(r_,
Г...:.О_,
W...:)~
Рис
14
6
Дисперсионная
сила
давления,
действующая
на
поляризуемую
частицу,
располо
женную
в
точке
г
=
Го.
Сила
порождается
коррелированными
флуктуациями
заряда
частицы
и
других
окружающих
ее
2ел
Последнее
обстоятельство
учитывается
посредством
функции
Грина
G,
рассчитанной
в
точке
расположения
частицы
щим
диполем
равны
нулю,
поскольку
они
возникают
в
различных
физических
систе
мах
Аналогичным
образом
отсутствуют
корреляции
между
индуцированными
вели
чинами.
Выразив
J1
и
Е
в
(14.54)
через
их
фурье-образы
и
используя
тот
факт,
что
E(t)
=
=
E*(t),
получаем
х
(F(ro)) = L J J
(JL~in)«(U)VE;(fI)(ro,(U'))
ei«.J'-«I)tduJ'duJ
+
,
-х
:х:
+ L J J
(Д~П)«(U)VЕ;(iП)(го,(U'))
е~(«I'-<<I)tduJ'duJ.
(14.57)
~
-х
Подставляя
линейные
соотношения
(14.55)
и
(14.56)
и
упорядочивая
слагаемые,
представим
первое
слагаемое
как
функцию
(Е(fI)),
а
второе
слагаемое
-
как
функ
~(П)
цию
J1
:
х
(F(ro)) = L J J
а\
«(U)V
2
(Е;(fI)
(го,
(U)
Е;
(fI)
(го,
(U'))
e
'
(«I'-<<I)t,
dUJ'
dUJ
+
I
-'Х)
ос
+
L
J J
w,2
~
'"
С*
(
")
(~(П)
(
)~~(П)
(
'))
1(<<1'
-«I)t..1
.
.1..1
..
2 V \ "
го,
го,
(U
J1.~
(U
J1.
J
(U
е
иш
иш,
С
со
7.1
__
(14.58)

14.3
Флукmуацuонно-uндуцuрованные
сuлы
417
где
'v'
n
означает
градиент
по
n-й
пространственной
переменной
в
аргументе.
Исполь
зуя
флуктуационно-диссипационную
теорему
для
диполя
и
полей
«(14.19)
и
(14.32»
и тот
факт,
что
......
'v'
1
G(r,
го;
W)
= 'V'2G(r,
го;
w), (14.59)
запишем
силу
в
компактной
форме:
00
(F(ro)) = L J + [
:"'/kT]
1т
[al(W)'V'lG
1t
(ro,ro;w)]
(М.
.
1ГС
со
1 -
е
t
-ос
(14.60)
Отметим,
что
сила
определяется
свойствами
среды,
которые
закодированы
в
функции
+-+
~
Грина
G.
Сила
исчезает
в
отсутствие
каких
бы
то
ни
было
объектов,
т.
е.
когда
G
рав
на
функции
Грина
свободного
пространства.
Равенство
(14.60)
позволяет
рассчитать
силу,
действующую
на
малую
поляризуемую
частицу
в
произвольном
окружении.
Равенство
справедливо
для
изотропных
частиц,
но
его
можно
обобщить
на
случай
анизотропных
поляризуемостей,
таких
как
молекулы
с
постоянными
дипольными
моментами
перехода.
14.3.1.
Потенциал
Казимира-ПОJIдера.
В
этом
разделе
мы
получим
силу,
действующую
на
частицу
с
поляризуемостью
аl со
стороны
другой
частицы
с
поляри
зуемостью
а2.
Как
показано
на
рис.
14.7,
две
частицы
расположены
на
расстоя
нии
R
друг
от друга.
На
малых
рассто
яниях
сила меняется
как
R-7,
тогда
как
на
больших
расстояниях
-
как
R-
8
.
Ис
ходя
из
интуитивных
соображений,
мож
но
сказать,
что
более
сильная
зависи
мость
от
расстояния
на
БОЛblUИХ
рассто
яниях
вряд
ли
возможна,
поскольку
спад
электромагнитного
поля
становится
сла
бее
при
переходе
от
ближних
полей
к
дальним.
Как
будет
показано,
при
темпе
ратуре
Т
=
О для
любых
расстояний
сила
Рис
147.
Определение
координат
для
рас-
чета
дисперсионной
силы
взаимодействия
между
двумя
поляризуемыми
частицами
может
быть
получена
из
единственного
потенциала
U(Т),
называемого
потенциа
лом
Казuмuра-Полдера
(Casimir-Polder potential).
Конечные
температуры
лишь
в
незначительной
мере
влияют
на
силу
[5],
и,
следовательно,
можно
ограничиться
проведением
анализа
для
случая
Т
=
О.
в
равенстве
(14.60)
сила
определена
посредством
функции
Грина
G.
Поэтому
получим
функцию
Грина
в
присутствии
поляризуемой
частицы
с
поляризуемостью
Н2,
центр
которой
расположен
в
точке
Г2.
Поле
Е
в
точке
r
можно
выразить
через
диполь
в
точке
Г2
следующим
образом:
~
(J}
1 """0
~ ~
E(r,w)
=
2'-G
(r,rl;w)Jl.l(W) +
Es(r,w),
с
со
(14.61)
"""0
где
q
означает
диадную
функцию
Грина
в
свободном
пространстве.
Рассеянное
поле
E
s
создается
частицей,
находящейся
в
точке
Г2:
~
v}
1 """0
~
Es(r,w)
=
2'-G
(r,r2;w)Jl.2(W) =
с
со
(J}
1
[(J}
1
"""0
"""0]
~
=
2'-
2'-G
(r,r2;w)a2(w)G
(r2,rl;w)
Jl.l(W).
с
СО
с
СО
(14.62)
27
Л
НовотныЙ.
Б
Хехт

418
Гл.
14.
Взаимодействия,
обусловленные
флуктуациями
Комбинируя
(14.61)
и
(14.62),
определяем
функцию
Грина
системы
«свободное
про
странство
+
частица
в
точке
r2.
как
(14.63)
(14.64)
ПОЛОЖ2;lМ
rl =
О
и
r2
=
(х,
О,
О)
=
xn
x
.
Теперь
получим
сумму
диагональных
элемен
тов
'VG
L'VIG,,(rl,rl;w)
=::
:0
Q2(W)
~
[:xG~;(~,O;w)]
G?,(l,O;w), (14.65)
1
~
<--+0
где
мы
использовали
свойства
функции
Грина
свободного
пространства
G .
Подстав-
<--+0
ляя
явную
форму
G
в
приведенное
выше
выражение
(ср.
с
разд.
8.3.1),
получаем
L
с2
1 exp(2lxwjc) [
(W
)
'VIG
I1
(rl,rl;w)
=
2"-
2 7
Q2(W)
-9
+
18~
-х
+
W
со
871"
Х
С
I
+
16
(~:l:/
-8i
(~x)
3 - 3
(~x)
4 + i
(~x)
5]
nJ:
=
~
'VIGi~(X;
w).
(14.66)
Введем
теперь
эту
функцию
Грина
в
формулу
для
силы
(14.61),
которая
при
Т
=
О
имеет
вид
(F(x)) =
-+-
ooJ
w
2
Im
[Ql(W)
L'VIGi~(X;W)]
dы.
7I"C
СО
О
t
(14.67)
Здесь
мы
использовали
тот факт,
что
вклады
с
отрицательными
частотами
равны
нулю
(ср.
(14.20».
Прямым
вычислением
можно
показать,
что
'V
х
(F) =
О
и,
следовательно,
сила
эта
потенциальна.
Поэтому
можно
получить
выражение
для
силы
через
потенциал
и
интегрированием
по
переменной
х:
и
= - J
(F(з·))(lх
=
(14.68)
Выполним
замену
переменной
интегрирования
w =
wc
и
заменим
расстояние
между
частицами
на л.
Понятно,
что
подынтегральное
выражение
представляет
собой
аналитическую
функцию
в
верхнем
полупространстве
переменной
интегрирования
и
что
оно стремится
к
нулю
при
w
-t
00.
Поэтому
можно
проинтегрировать
выражение
по
мнимой
оси,
используя
равенство
00
х
r
j(w)dЫ
= i r
f(i"1)d"1.
(14.69)

14
3.
Флукmуацuонно-uндуцuрованные
силы
419
Комбинируя
эти
математические
трюки,
получаем
потенциал
взаимодействия
частиц:
ос
U=-
~C2
6 J
0:1
(U;''1)0:2(k''T/)e-
211R
[З+677R+5(77R)2+2(77R)3+(1/R)4]
(11/.
161Г
E:oR
о
(14.70)
Мы
использовали
тот факт,
что
О:z(П)
-
чисто
вещественная
величина
на
мнимой
оси
П
=
i'ГJ.
Равенство
(14.70) -
знаменитый
потенциал
Казимира-Полдера
-
спра
ведливо
при
любых
расстояниях
R
между
частицами.
Наши
результаты
согласуются
со
строгими
расчетами,
основанными
на
квантовой
электродинамике
в
рамках
чет
вертого
порядка
теории
возмущений
[13].
Представленный
здесь
вывод
позволяет
включить
поправки
более
высокого
порядка
путем
простого
добавления
дополнитель-
+-+
ных
слагаемых
взаимодействия
в
функцию
Грина
G
в
(14.63).
Формулу
для
силы
можно
выразить
через
потенциал
посредством
равенства
(F)
= - 'VU.
Представляет
интерес
расчет
потенциала
в
предельных
случаях
больших
и
малых
расстояний.
На
малых
расстояниях
удерживаем
лишь
первое
слагаемое
в
скобках,
полагая
ехр(
-2'ГJR)
=
1,
откуда
получаем
U(R
_
О)
= -
6~
2
~
s:
0:1
(i'ГJ)0:2(i17)d1/'
З21Г ео
R
(14.71)
Это
потенциал
Ван-дер-Ваальса,
имеющий
место
при
малых
расстояниях
R.
Потен
циал
зависит
от
дисперсионных
свойств
поляризуемости
частицы
и
меняется
обратно
пропорционально
шестой
степени
расстояния
между
частицами
R.
Чтобы
получить
предельное
выражение
для
больших
R,
выполним
подстановку
U =
'ГJR
в
(14.70),
которая
приводит
к
следующему
выражению
для
потенциала
взаимодействия
частиц:
00
И
= -
~C2
7 J
0:1
(icu/
R)0:2(icu/
R)e-
2u
[3
+
6и
+ 5u
2
+
2u
З
+ tt
4
]
(1u.
161Г
toR
о
(14.72)
Затем,
в
пределе
R _
00,
заменим
поляризуемость
ее
постоянным
значением
а,(О).
После
вынесения
поляризуемостей
из-под
знака
интеграла
получим
х
U(R
_ (0) = -
п~
2
0:1(0)~2(0)
J
е-
2и
[3
+
6и
+ 5u
2
+
2u,З
+
'и
4
]
(1'/1..
161Г
ео
R
(14.73)
о
Наконец,
используя
равенство
х
J
'11
-
2u
d
n!
и
е
и
= 2
n
+
1
Yn~O,
(14.74)
о
берем
интеграл
в
(14.73)
аналитически,
после
чего
получаем
потенциал
Казимира
Полдера
в
пределе
больших
расстояний:
U(R
)
= _
2З1iс
0:1
(0)0:2(0)
_00
32
7 .
641Г ео
R
(14.75)
Этот
результат
-
проявление
флуктуаций
вакуума.
Он
носит
название
потенциала
Казимира
и
был
впервые
получен
в
1948
г.
Хендриком
Казимиром
[14].
Потен
циал
примечателен
тем,
что
меняется
обратно
пропорционально
седьмой
степени
расстояния
R
между
частицами.
Таким
образом, на
больших
расстояниях
эта
сила

420
Гл
/4
Взаимодействия,
обусловленные
флуктуациями
спадает
гораздо
быстрее,
чем
на
малых.
Такое
поведение
противоположно
зависи
мости
плотности
электромагнитной
энергии
от
расстояния,
которая
демонстрирует
более
быстрый
спад
(R-
6
)
вблизи
источника.
Потенциал
Казимира
зависит
толь
ко
от
статических
(w
=
О)
поляризуемостей,
а
значит,
их
спектральные
свойства
не
имеют
значения.
Отметим,
что
при
выводе
потенциала
Казимира-Полдера
мы
рассмотрели
только
градиентную
силу
и
пренебрегли
влиянием
силы
рассеяния.
Последняя
не
является
консервативной
и
должна
обращаться
в
нуль,
если
ча
стица
(частицы)
находится
в
термодинамическом
равновесии
с
вакуумным
полем.
Следует
подчеркнуть,
что
потенциал
Казимира-Полдера
проистекает
исключи
тельно
из
нулевых
флуктуаций
и
не
учитывает
флуктуаций
тепловых.
Обычно
при
комнатной
температуре
силы,
обусловленные
теплом,
по
крайней
мере
на
порядок
слабее
сил,
связанных
с
флуктуациями
вакуума
[5].
14.3.2.
Электромагнитное
трение.
Электромагнитные
взаимодействия
между
двумя
электрически
нейтральными
объектами
при
водят
не
только
к
консервативным
дисперсионным
силам, но
и к
н,екон,серватuвн,ой
силе
трения,
если
два
объекта
движутся
друг
относительно
друга.
Эта
сила
трения
связана
только
с
тепловыми
флуктуациями
и
замедляет
движение
объекта
практически
до
нуля.
Хотя
эта
сила
мала,
но
она
порождает
важные
следствия
для
разработки
наноэлектромеханических
систем
(НЭМС)
и
для
различных
приложений
в
квантовой
информации.
Электромаг
нитное
трение
при
водит
к
росту
декогерентности
в
миниатюризированных
ловушках,
таких
как
ионные
ловушки
и
атомные
чипы,
а
также
к
ограничению
добротности
механических
резонансов.
Рассмотрим
малую
электрически
нейтральную
частицу,
такую
как
атом,
моле
кула,
кластер
или
наноструктура,
размеры
которой
меньше
характерных
длин
волн
л.
В
этом
приближении
частицу
можно
представить
поляризуемостью
a(w).
Пусть
частиц~
расположена
в
произвольном
окружении,
которое
описывается
функцией
Грина
G.
Предположим,
что
движение
центра
масс
частицы
x(t)
задается
классиче
ским
уравнением
Ланжевена:
-х
"((t
- t').!!,x(t')dt' +
mШ6х(t)
= Fx(t),
dt
(14.76)
где
m -
масса
частицы,
"((t) -
коэффициент
релаксации,
проистекающий
из
теп
ловых
флуктуаций
электромагнитного
поля,
Ша
-
собственная
частота
колебаний
частицы,
а
Р,
(t) -
стохастическая
сила.
Отметим,
что
возвращающая
сила
mШ6х(t)
добавлена
для
общности
и
никак
не
повлияет
на
окончательный
результат.
В
состоя
нии
термодинамического
равновесия
Fx(t)
представляет
собой
стационарный
стоха
стический
процесс,
среднее
по
ансамблю
которого
равно нулю.
Спектр
мощности
силы
Sг(w)
дается
теоремой
Винера-Хинчина
(ср.
(14.16)):
х
SF(w)
=
2~
f
(Fx(T)Fx(O))e'UJT
dT,
(14.77)
-00
где
w -
угловая
частота.
Далее,
в
состоянии
теплового
равновесия
SF
связана
с
коэф
фициентом
трения
флуктуационно-диссипационной
теоремой.
Поскольку
движение
макроскопической
частицы
классическое,
рассмотрим
классический
предел,
т.
е.
kT-:У(w)
= nSF(w),
(14.78)
где
;:Y(w)
-
фурье-образ
"((t),
определенный
только
для
t >
о.

14
3.
Флук.mуационно-индуцированные
силы
421
Мы
подразумеваем,
что
слагаемое,
соответствующее
общей
силе
трения,
в
равен
стве
(14.76)
в
момент
времени
t
зависит
от
скорости
частицы
в
более
ранние
моменты
времени.
Теперь
учтем,
что
время
взаимодействия
частицы
с
тепловым
резервуаром
короче
в
сравнении
с
динамикой
частицы,
и,
следовательно,
изменение
скорости
частицы
за
время
взаимодействия
очень
мало.
В
этом
марковском
приближении
трение
не
имеет
памяти
и,
таким
образом,
ос
"10
= f
"1
( t
)(и.
о
(14.79)
Вычисляя
(14.78)
при
ш
=
О
и
используя
(14.79),
находим,
что
постоянная
релаксации
связана
со
спектром
мощности
следующим
равенством:
(14.80)
Последнее
равенство
задает
связь
между
линейным
коэффициентом
релаксации
скорости
и
спектром
мощности.
Чтобы
рассчитать
"10,
следует
найти
спектр
силы,
который,
в
свою
очередь,
определяется
электромагнитными
полями
посредством
флуктуаций
токов
в
окружающей
среде
и
флуктуаций
диполя
(ср
(14.54».
При
меняя
теорему
Винера-Хинчина
(14.77),
преобразование
Фурье
дипольной
силы
(14.54)
и
считая
флуктуации
стационарными,
получаем
(F;(ш')Fх(ш))
=
SF(ш)8(ш
-
ш')
=
3 ,
= L
([
(д;(fI)
(ш')
+
Д;(iП)
(ш')
) *
(:хЕ;(fl)
(ш')
+
:а;~;(iI1)(ш'))]
х
•.
j=!
Х
[(Д~fl)(ш)
+
дiiП)
(ш))
*
(:хЕ}fl)(ш)
+
:'т.Е,~iП)(ш))]).
(14.81)
где
*
означает
свертку.
Каждое
аддитивное
слагаемое
в
(F,*(ш')F.,
(ш'))
представ
ляет
собой
корреляционную
функцию
четвертого
порядка,
заданную
в
частотной
области.
Поскольку
флуктуационно-диссипационная
теорема
включает
корреляци
онные
функции
второго
порядка
и не
включают
корреляционных
функций
четвер
того
порядка,
найти
решение
в
рамках
квазиравновесной
статистической
механики
не
представляется
возможным.
Однако
выход
есть:
тепловые
флуктуации
можно
мыслить
как
суперпозицию
большого
числа
излучающих
осцилляторов
с
широким
спектром,
и в
этом
случае
можно
применить
центральную
предельную
теорему.
Благодаря
широкому
спектру,
то
же
справедливо
для
флуктуаций
дипольных
мо
ментов.
Стохастические
процессы
со
статистикой
Гаусса
обладают
тем
свойством.
что
корреляционную
функцию
четвертого
порядка
можно
выразить
суммой
по
парных
произведений
корреляционных
функций
второго
порядка.
Таким
образом,
равенство
(14.81)
можно
рассчитать,
зная
КФ
тепловых электромагнитных
полей
и
КФ
электрических
дипольных
моментов
второго
порядка.
В
состоянии
теплового
равновесия
эти
корреляционные
функции
даются
флуктуационно-диссипационной
теоремой
(14.19)
и
(14.32).
Таким
образом,
у
нас
есть
все
ингредиенты
для
рас
чета
коэффициента
релаксации
"10
в
равенстве
(14.80).
Заменим
индуцированное
слагаемое
в
(14.81)
флуктуационным
слагаемым
с
помощью
линейных
соотношений
(14.55)
и
(14.56).
Затем
применим
флуктуационно-диссипационные
теоремы
(14.19)
и
(14.32).
Наконец,
используем
соотношение
(14.80),
посредством
которого
найдем
спектр
постоянной
релаксации
"10.
Четыре
аддитивных
слагаемых
в
(14.81)
при
ВО-

422
Гл
14
Взаимодействия,
обусловленные
флуктуациями
дят
К
четырем
аддитивным
постоянным
релаксации,
две
из
которых
пренебрежи-
мо
малы.
Можно
показать,
что
трение
исчезает
при
Т
---+
о,
это
означает,
что
трение
связано
только
с
тепловыми
флуктуациями,
а
не
с
квантовыми
нулевыми
флуктуациями.
Фактически,
этот
результат
также
следует
из
требования
инвариантности
нулевых
флуктуаций
относительно
преобразований
Лоренца
[15].
Далее,
другой
примечатель
ный
результат
состоит
в
том,
что
трение
имеет
место
даже
в
пустом
пространстве при
конечной
температуре.
Таким
образом,
движущийся
в
пустом
пространстве
объект
в
конце
концов
придет
в
состояние
покоя.
В
приближении
свободного
пространства
получаем
х х
/'0 =
/1:
.)
f
!<k((А))I2"Л7((А),
T)dы
+ 2
~2
f
Im[a((A))](A)5
11
((A),
T)dы,
187Г'
('
cokT
37Г
с
cokT
(14.82)
о о
где
(14.83)
Первое
слагаемое
в
(14.82)
согласуется
с
результатом
Боера
(Воуег)
[15],
тогда
как
второе
получено
независимо
в
[16]
и
[17].
В
работе
[17]
электромагнитное
трение
про
анализировано
для
особого
случая
поляризуемой
сферической
частицы
радиуса
а,
расположенной
вблизи
полубеско
нечного
полупространства
(подложка)
с
комплексной
диэлектрической
проницаемо
стью
Е2«(А)).
Аналогичные
исследования
представлены
в
[18]
и
[19].
Предполагается,
что
частица
движется
параллельно
поверхности
вдоль
оси
х
на
высоте
Zo
(см.
рис.
14.8).
Эти
исследования
выявили
не
только
сильную
зависимость
постоянной
с\
= 1
Рис
148
Частица
движется
в
вакууме
параллельно
плоской
подложке,
диэлектрическая
проницаемость
которой
равна
C2(W)
релаксации
от
расстояния,
но
также
и
сильную
зависимость
от
материальных
свойств
частицы
и
подложки.
В
качестве
примера
приведем
рис.
14.9,
на
котором
показана
нормированная
спектральная
плотность
коэффициента
релаксации
как
функция
уг
ловой
частоты
(А)
при
температурах
Т
= 3
К,
30
К,
300
К.
Коэффициент
релаксации
/'0
получается
путем
интегрирования
кривых
по
всем
частотам,
т.
е.
1'0
численно
равен
площади
под
спектральными
кривыми.
На
рисунке
показаны
результаты
для
двух
различных
конфигураций
вещества:
(а)
образец
и
частица
сделаны
из
се
ребра
и
(6)
образец
и
частица
сделаны
из
стекла.
Явно
видно,
что
спектральный
диапазон
/'
гораздо
короче
на
рис.
14.9,
а,
чем
на
рис.
14.9,6,
амплитуда
гораздо
ниже.
Таким
образом,
гораздо
более
короткий
спектр
диэлектрической
системы
при
водит
к
значительно
большей
амплитуде
релаксации
в
сравнении
с
металлической
системой.
Результаты
численного
интегрирования
приведены
в
табл.
14.1.
Важное
следствие
заключается
в
том,
что
коэффициент
релаксации
в
значительной
степени
определяется
вешеством
полубесконечной
подложки
(см.
[17]).
Свойства
же
частицы
