Островський А.Л., Мороз О.І., Тарнавський В.Л. Геодезія, частина II

Подождите немного. Документ загружается.

Підставивши в (IV.2.23) ці числові значення, отримаємо.

1 3438' гг „ ,

п = —

• л/З

= 4,96 « 5сторін.

400 З'

Для 5 = 200 м; [5] = 200 м • 5 = 1000 м інструкція допускає 1000 м

для масштабу 1:5000 та 500 м для масштабу 1:2000.

Насправді такі довжини мензульних ходів не можна допускати.

Справа в тому, що висячий мензульний хід довжиною [ 5 ] = 1000 м (якщо п

= 5; 5! = 200 м;

= т>

матиме похибку М = 1,70 м при

допустимій (для масштабу 1:5000), М'

доя

= 1,0 м (0,2 мм плану).

Недопустимим буде й аналогічний хід, прокладений між точками з

відомими координатами. Дещо більше половини похибки ходу складає

похибка графічної побудови горизонтальних кутів (53%). Це означає, що під

час розрахунків допусків мензульних ходів слід обмежувати не тільки

довжини ходів, але й число сторін. Розрахунки показують, що максимальна

довжина мензульного ходу може бути рівною 600 м (3 лінії по 200 м) і його

похибка складатиме 1,08 м, тобто, практично рівна допустимій для масшта-

бу знімання 1:5000.

Аналогічні розрахунки допустимих мензульних ходів із відносною

похибкою вимірювання ліній 1:400 під час знімання в масштабі 1:2000,

1:1000 і 1:500 також показали, що подані в інструкції допустимі довжини

ходів та кількість ліній у них завищені.

Нижче, у таблиці ІУ.2.2, подані розраховані допустимі мензульні

ходи.

Довжина ходу для масштабу 1:500 розрахована, для випадку, коли

вимірювання ліній виконується не нитковим віддалеміром, а мірною

стрічкою або рулеткою з відносною похибкою 1:1000 або 1:2000, як цього

вимагає інструкція.

Таблиця ІУ.2.2

Параметри допустимих мензульних ходів під час великомасштабного

знімання

Масштаб Максимальні Максимальні

Максимальна

знімання довжини ходу, м довжини ліній, м

кількість ліній в ході

1:5000 600 200

1:2000 250

125

1:1000

100

50 2

1:500

Хід масштабу 1:500 може складатися із двох ліній по 25 м кожна.

Слід зауважити, що в розрахунках допустимої довжини висячих мен-

зульних ходів (саме такі ходи часто використовуються) брались до уваги

409

тільки похибки вимірювання ліній та похибки побудови горизонтальних

кутів. Неминучі, абсолютні, випадкові похибки відкладання ліній за

допомогою циркуля-вимірника та поперечного масштабу, які дорівнюють

0,1-0,2 мм плану (граничні - 0,3 мм), практично незалежні від довжин ліній

(зазвичай, декілька сантиметрів у даному масштабі плану), не врахо-

вувались.

Тому, для компенсації впливу цих похибок, доцільно виконувати

вимірювання ліній для мензульних ходів мірною стрічкою або рулеткою не

тільки під час знімання в масштабі 1:500, але й у масштабах 1:1000, 1:2000,

1:5000.

Заміна висячих ходів ходами між точками з відомими координатами

також підвищує їх точність.

Інструкція дозволяє використовувати під час мензульного знімання

геометричну мережу трикутників, але тільки під час знімання в масштабі

1:5000.

IV. 2.7. Розрахунок точності та допустимої довжини теодолітного

ходу

Нехай теодолітний хід прокладено між відомими пунктами. Скорис-

таємось формулою, виведеною в розділі II:

Ґ і, \

Ґ \2 . „.2

— ' (ІУ.2.24)

М_

[4і "дт;

іг7

Найдемо екстремальне значення число сторін ходу п. Для цього про-

диференціюємо (ІУ.2.25) по и і результат прирівняємо до нуля:

М) -1 (ЧУ, ' <

дп п

{8 ) 12 р'

Після перетворень отримаємо:

иЧ 5 ;

р'

' т

' г

(ІУ.2.25)

1 3438' сг ... ,,

п = л/12 =11,9 = 12 сторін.

2000 0,5'

Кути вимірюють теодолітом із точністю відліку І < 30" двома прийо-

мами, а труба наводиться на віху з віхоутримувачем. Тому приймемо

- 0,5'. Нехай лінії вимірюються стрічкою з відносною похибкою 1/2000.

На основі (ІУ.2.24) розрахуємо, які довжини ходів можна допускати

для різних масштабів знімання.

410

В класичній геодезії нев'язки ходів Д^ допускаються в два рази

більші за допустимі похибки координат М

Шкор

, оскільки після зрівнова-

ження ходів похибки координат зменшаться приблизно в два рази. Проте,

при цьому значна кількість точок ходу буде мати похибки координат, рівні

допустимим, що для паперових карт небажано, а для ЦММ взагалі не слід

допускати тому, що на ЦММ вимірювання координат, довжин, виконуються

не графічно, а аналітично. В таблиці ІУ.2.3 наведені розрахунки параметрів

ходів для М

дол

= 2М

допкор

= /^ та для М

доп

=М

допкор

. Останні значення

параметрів взяті в дужки.

Зрозуміло, що при цьому математична основа карт буде в двічі

точнішою. Сучасні точності вимірювання кутів та ліній дозволяють це

реалізувати. Вважаємо, що більш точну математичну основу, а також більш

точні плани та карти необхідно мати вже сьогодні.

Таблиця ІУ.2.3

Допустимі параметри теодолітних ходів для різних масштабів знімання, які

прокладаються з відносною похибкою вимірювання ліній 1:2000 та кутів

=30".

Масштаб

знімання

Максимальні довжини

ходів, м

Довжини

сторін, м

Кількість

сторін в ході

1:5000

9000-7500 (4500-3700)

750-250 (375-125)

12/30

1:2000

4000-3200 (2000-1700)

400-100 (200-60)

10/30

1:1000

2000-1700 (1000-850)

200-85(100-40)

10/20

1:500

1000-850 (450-400)

125-40 (60-20)

8/20

IV.

2.8. Розрахунок планової точності та допустимої довжини

тахеометричного ходу

Для визначення екстремального значення числа сторін п та М

мп

= Д^

тахеометричного ходу, скористаємося формулами (ГУ.2.24) та (ІУ.2.25).

Проте, необхідно врахувати, що лінії в тахеометричному ході вимі-

рюються оптичними віддалемірами з відносною похибкою

= —, (IV.2.26)

5 400

а горизонтальні кути вимірюються не грубіше за 1'.

Підставивши в (ІУ.2.25) ці числові значення, отримаємо:

1 3438' _

п - -— —л/12 = ЗО сторін .

400 1' ^

За такої кількості сторін, якщо їх середня довжина 5 = 100 м, довжина

ходу буде [5] = 3000 м.

413

Розрахунки за формулою (IV.2.24) показали, що очікувана нев'язка та-

кого ходу /^ =

1,99

м = 2,0 м, тобто, допустима для масштабу знімання 1:5000.

Такі ж розрахунки показали, що для масштабу знімання 1:2000

довжину тахеометричного ходу можна допустити приблизно 1000 м. Що

стосується масштабів 1:1000, 1:500, для них прокладати тахеометричні ходи

з відносною похибкою вимірювання ліній 1/400 недоцільно (допустимі ходи

дуже короткі).

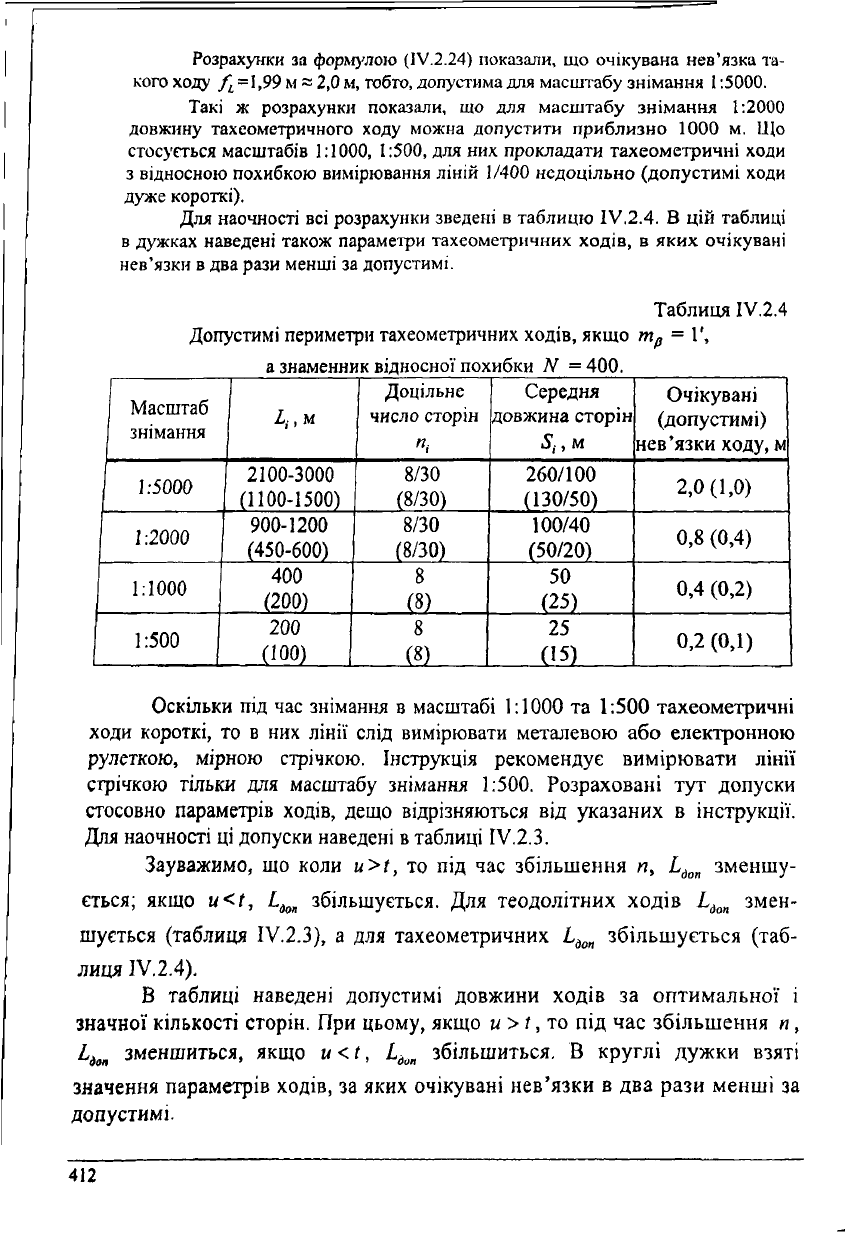
Для наочності всі розрахунки зведені в таблицю ІУ.2.4. В цій таблиці

в дужках наведені також параметри тахеометричних ходів, в яких очікувані

нев'язки в два рази менші за допустимі.

Таблиця ІУ.2.4

ДОПУСТИМІ Периметри тахеометричних ХОДІВ, ЯКЩО

ТПр

= 1

а знаменник відносної похибки N =400.

Масштаб

знімання

А>м

Доцільне

число сторін

«І

Середня

довжина сторін

5„и

Очікувані

(допустимі)

нев'язки ходу, м

1 2100-3000

5000

( (1100-1500)

8/30

(8/30)

260/100

(130/50)

2,0(1,0)

1:2000

900-1200

(450-600)

8/30

(8/30)

100/40

(50/20)

0,8 (0,4)

1:1000

400

(200)

(8)

(25)

0,4 (0,2)

1:500

200

(100)

(«)

(15)

0,2 (ОД)

Оскільки під час знімання в масштабі 1:1000 та 1:500 тахеометричні

ходи короткі, то в них лінії слід вимірювати металевою або електронною

рулеткою, мірною стрічкою. Інструкція рекомендує вимірювати лінії

стрічкою тільки для масштабу знімання 1:500. Розраховані тут допуски

стосовно параметрів ходів, дещо відрізняються від указаних в інструкції.

Для наочності ці допуски наведені в таблиці ІУ.2.3.

Зауважимо, що коли и>і, то під час збільшення п, Ь

доп

зменшу-

ється; якщо и<(, І

збільшується. Для теодолітних ходів Ь

доп

змен-

шується (таблиця ІУ.2.3), а для тахеометричних Ь

доп

збільшується (таб-

лиця ІУ.2.4).

В таблиці наведені допустимі довжини ходів за оптимальної і

значної кількості сторін. При цьому, якщо и > і, то під час збільшення п,

А><и зменшиться, якщо и < і, 1

6ж

збільшиться. В круглі дужки взяті

значення параметрів ходів, за яких очікувані нев'язки в два рази менші за

допустимі.

412

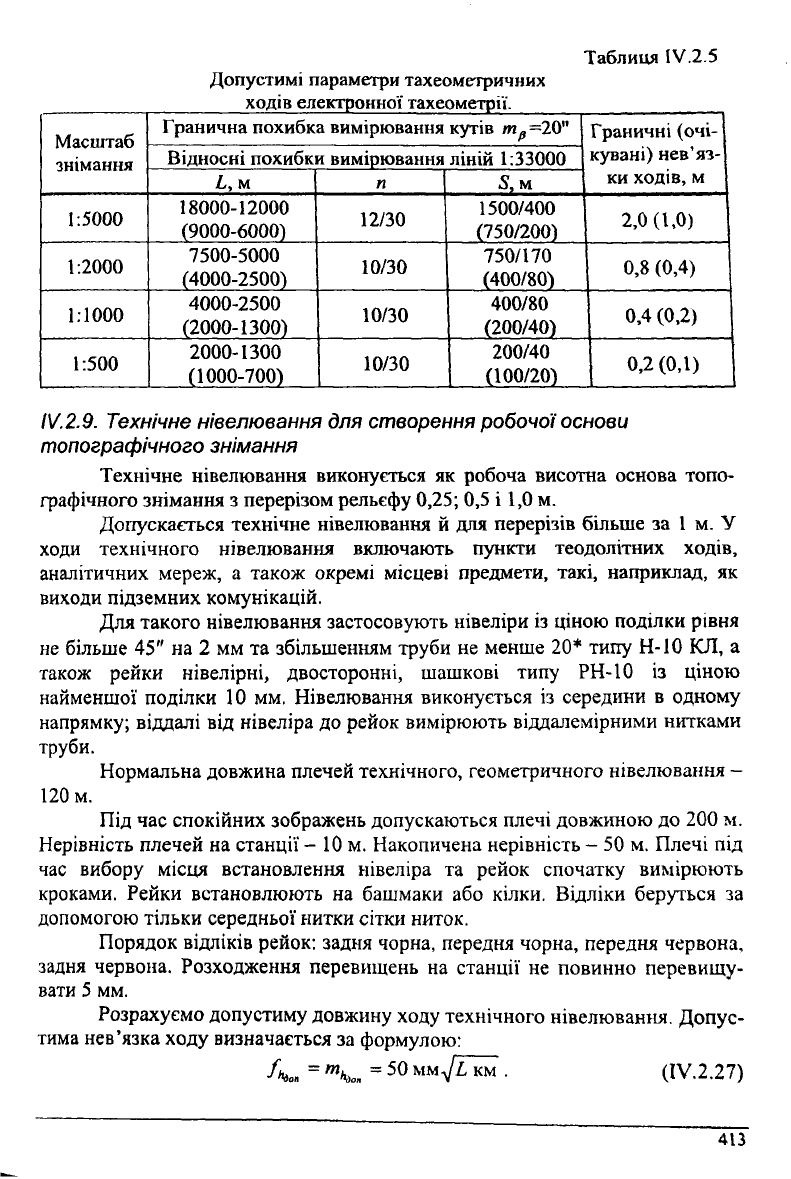
Таблиця ІУ.2.5

Допустимі параметри тахеометричних

ходів електронної тахеометрії.

Масштаб

знімання

Гранична похибка вимірювання кутів /и^=20"

Граничні (очі-

кувані) нев'яз-

ки ходів, м

Масштаб

знімання

Відносні похибки вимірювання ліній 1:33000

Граничні (очі-

кувані) нев'яз-

ки ходів, м

Масштаб

знімання

і, м п

5, м

Граничні (очі-

кувані) нев'яз-

ки ходів, м

1:5000

18000-12000

(9000-6000)

12/30

1500/400

(750/200)

2,0(1,0)

1:2000

7500-5000

(4000-2500)

10/30

750/170

(400/80)

0,8 (0,4)

1:1000

4000-2500

(2000-1300)

10/30

400/80

(200/40)

0,4(0,2)

1:500

2000-1300

(1000-700)

10/30

200/40

(100/20)

0,2(0,1)

N.2.9. Технічне нівелювання для створення робочої основи

топографічного знімання

Технічне нівелювання виконується як робоча висотна основа топо-

графічного знімання з перерізом рельєфу 0,25; 0,5 і 1,0 м.

Допускається технічне нівелювання й для перерізів більше за 1 м. У

ходи технічного нівелювання включають пункти теодолітних ходів,

аналітичних мереж, а також окремі місцеві предмети, такі, наприклад, як

виходи підземних комунікацій.

Для такого нівелювання застосовують нівеліри із ціною поділки рівня

не більше 45" на 2 мм та збільшенням труби не менше 20* типу Н-ІО КЛ, а

також рейки нівелірні, двосторонні, шашкові типу РН-10 із ціною

найменшої поділки 10 мм. Нівелювання виконується із середини в одному

напрямку; віддалі від нівеліра до рейок вимірюють віддалемірними нитками

труби.

Нормальна довжина плечей технічного, геометричного нівелювання -

120 м.

Під час спокійних зображень допускаються плечі довжиною до 200 м.

Нерівність плечей на станції -10 м. Накопичена нерівність - 50 м. Плечі під

час вибору місця встановлення нівеліра та рейок спочатку вимірюють

кроками. Рейки встановлюють на башмаки або кілки. Відліки беруться за

допомогою тільки середньої нитки сітки ниток.

Порядок відліків рейок; задня чорна, передня чорна, передня червона,

задня червона. Розходження перевищень на станції не повинно перевищу-

вати 5 мм.

Розрахуємо допустиму довжину ходу технічного нівелювання. Допус-

тима нев'язка ходу визначається за формулою:

Ль.

"V, =

. (ІУ.2.27)

413

Інструкція [5] допускає похибку у висоті точок робочої основи 1/10 від

перерізу рельєфу. Якщо нев'язка ходу 1/5 від перерізу рельєфу, то після ув'я-

зування ходу максимальна похибка у висоті буде в середині ходу й виявиться

рівною « 1/2 від нев'язки, тобто, 1/10 від перерізу. Тому приймемо т

Ніип

=1/5

від перерізу

А.

Для перерізу

м = 100 см, =

5 •

100 см = 20 см = 200 мм .

Розв'яжемо рівняння (ІУ2.27) відносно Ь. Отримаємо:

Дкм) =

в = ~ = 16км.

(50 мм)

2500 2500

Для

= 0,5 м Ь = 4

км;

для

= 0,25 м Ь =

км.

Наші розрахунки довжин ходів співпадають з екстремальними

допусками інструкції.

IV.2.10. Тригонометричне нівелювання для створення висотної

знімальної основи

З методами тригонометричного нівелювання студенти знайомі з

курсу "Топографія". Саме метод тригонометричного нівелювання застосо-

вують для визначення перевищень та висот під час тахеометричного

знімання. У даному випадку ми розглядаємо тригонометричне нівелювання

як метод побудови висотних робочих мереж для будь-якого способу

топознімання. Кути нахилу місцеві V вимірюють оптичними або електрон-

ними тахеометрами. Рекомендується виконувати вимірювання кутів нахилу

трьома прийомами при двох положеннях вертикального круга. Коливання

значень місця нуля (МО) та кутів нахилу V не повинно перевищувати 15".

Інструкція рекомендує використовувати прилади з точністю відліків

вертикального круга 1-2".

Повна формула тригонометричного нівелювання має вигляд:

к = + ;-/ + /, (ІУ.2.28)

де 5 - горизонтальне прокладення довжини лінії; V - кут нахилу; і -

висота тахеометра; / - довжина рейки (труба наводиться на верх рейки); /-

поправка за сумісний вплив кривини Землі та рефракції.

Допустима нев'язка тригонометричного нівелювання визначається за

формулою:

/^ = 0,04^. (ІУ2.29)

В формулі (ІУ.2.29) - нев'язка в см; [5] - довжина ходу в м; и -

число ліній ходу.

Розрахуємо допустиму довжину тригонометричного ходу, виходячи з

формули (ІУ.2.29).

Тригонометричне нівелювання допускається інструкцією для пере-

різу к = 2 м і більше. Якщо к = 2 м, тоді Д ^ = = і к; Д^ = 40 см.

__ _ - - — ——

Розв'яжемо (ІУ.2.29) відносно [5 ].

0,04

(ІУ.2.30)

Як бачимо з формули (ІУ.2.30), допустима довжина ходу буде

зростати під час збільшення числа сторін ходу. Це закономірно, оскільки

нівелювання з короткими сторонами виконується точніше. Інструкція, без

обгрунтування, приймає допустиме число сторін 5, проте, допускає

збільшення числа сторін в 1,5 разів у гірських районах. Без втрати точності

нівелювання число сторін ходу можна збільшити.

Нехай п = 9. Тоді [5] м =

40 см

•

л/9

0,04

= 3000 м.

Таким чином, допустима довжина ходу « 3 км. Для перерізу рельєфу

більше 2 м допустимі довжини ходів, зрозуміло, будуть зростати.

Може виконуватися спеціальне тригонометричне нівелювання, коли

перевищення визначаються зі значно більшою точністю, ніж передбачено

формулою (ІУ.2.29).

Тригонометричне нівелювання широко застосовується під час визна-

чення висот перехідних точок, а також окремих точок, планове положення

яких визначається прямими й оберненими та комбінованими засічками.

Детально питання визна-

чення координат окремих точок

засічками описані в розділі, де

розглядаються прив'язування

пунктів полігонометрії до

пунктів тріангуляції або до

пунктів полігонометрії старших

класів. Там також подані й

розрахунки точності визначення

планових координат прямими,

оберненими та комбінованими

однократними та багатократ-

ними засічками.

Коротко зупинимося на

вживаних методах визначення

висот цих точок.

Зазвичай, висоти визна-

чаються методом "на себе", тоб-

то, визначається висота тієї точки, де знаходиться тахеометр, за відомими

висотами мінімум трьох найближчих точок, що розташовані навколо

шуканої точки. Горизонтальні віддалі 5,, , 5

від шуканої точки А до

відомих точок 1, 2, 3 визначаються з аналітичного розв'язку трикутників або

вимірюють світловіддалемірами (рис. IV.2.7).

Рис. ІУ.2.7. До визначення висот окремих

точок.

415

Кути нахилу V вимірюють трьома прийомами (кожний прийом при

двох положеннях вертикального круга). Вираховують середнє значення

кутів нахилу із трьох вимірів. Нехай ці кути будуть V, у

сеп

, У

сері

. Далі, за

формулою (1У.2.28) знаходять середні перевищення И

сеп

, Н

серг

, И

сері

. Визна-

чають три значення висоти шуканої точки А:

= Я, + ; Н

Аі

= Н

сер2

•

Л]

= Я

сер1

Знаки перевищень А беруть оберненими до виміряних, оскільки

визначається висота Н

точки А, а не висоти Н

. За кінцеву висоту точки

береться її середнє вагове значення

р,+р

+р

(ІУ.2.31)

с с с

де Р

=—; Р

= —; Р

= —; с - довільний коефіцієнт пропорційності.

5*1 З*

2 А

IV.2.11.

Вимірювання

зенітних віддалей. Вертикальна рефракція

В аналітичних мережах, а також під час

тахеометричного знімання для визначення пере-

вищень вимірюють кути нахилу к У тріангуляції,

коли виконується тригонометричне нівелювання для

визначення висот пунктів тріангуляції, вимірюють

не кути нахилу ц а зенітні кути 2. Хоча 2 - це кути,

їх часто називають ще й зенітними віддалями.

Залежність між кутами нахилу V та зенітними

кутами ї показана на рис. ІУ.2.8.

Нехай маємо нахилену пряму АВ, початкова

точка якої А співпадає з початком системи прямо-

кутних координат

ТАУ.

Площина 2АУ- вертикальна.

Як

видно з рис. ГУ.2.8:

2 = 90° -

(ІУ2.32)

або

у = 90'-2. (ІУ.2.33)

Рис. ІУ.2.8.

Залежність між

кутами нахилу ута

зенітними кутами 1.

Як відомо, для вимірювання кутів нахилу V вводиться поняття "місце

нуля" (М0). Під час вимірювання зенітних кутів (віддалей) вводиться

поняття

"місце зеніта"

(МІ). Це відлік вертикального круга тахеометра,

коли зорова труба спрямована в зеніт, а бульбашка циліндричного рівня, що

скріплений із вертикальним кругом, знаходиться в нуль-пункті. Формула

(ІУ.2.28) набуває вигляду.

= 5с&2„+і-/ + /,. (IV.2.34)

де і - висота тахеометра; І - довжина рейки (труба наведена на верх рейки).

416

Як і в (IV.2.28), / - поправка за кривину Землі к

та рефракцію г.

/ = к

~г.

к = 1*1

2К

= 1—

2 А. '

(ІУ.2.35)

(IV.2.36)

(ІУ.2.37)

Рис. IV.2.9. Спотворення

вертикальною рефракцією

виміряних V

та 2

У формулі (ІУ.2.36) К

- радіус

Землі рівний 6371 км. У формулі (ІУ.2.37)

- радіус кривої розповсюдження світ-

ла. Виникає питання, як визначити К

На

жаль, у неоднорідній за густиною атмос-

фері світло від точки В (де встановлена

візирна ціль) до точки А (де встановлено

тахеометр) розповсюджується не прямо-

лінійно, як це показано на рис. ІУ.2.8, а по

деякій складній кривій, як це показано на

рис. ІУ.2.9. У результаті, достатньо

направити трубу по дотичній АС до кривої

АВ, щоб спостерігач бачив в трубі точку В.

Спостерігач вважає, що труба

направлена по хорді АВ = 5. Насправді

труба направлена по дотичній АС. Тому вимірюються не теоретичні кути

V, та 2,, а спотворені рефракцією кути у

та 2

. Кут 8 називається частко-

вим кутом вертикальної рефракції. Це кут між дотичною АС та хордою АВ.

Куту 8 відповідає лінійна рефракція г. Саме на величину г спотворюється

правильне перевищення И між точками А та В.

Врахування рефракції 8 або г виявилось надзвичайно складною

справою, оскільки крива розповсюдження світла може бути повернута

випуклістю вверх або вниз. Окрім того, у різних частинах кривина кривої

різна.

Для визначення 8 або г необхідно знати густину повітря в багатьох

точках на шляху світла. А оскільки світло розповсюджується часто досить

високо над поверхнею землі, то це майже не можливо. Дослідження цього

питання виконуються майже 400 років.

Спочатку дослідники великі надії покладали на визначення єдиного

коефіцієнта рефракції. Під коефіцієнтом рефракції к розуміють відношення

, Яз

к = (ІУ.2.38)

Дійсно, вплив кривини Землі к

на перевищення визначається до-

статньо точно (за формулою ІУ.2.36).

417

Для відомого к знайдемо Л .

Отже

або

г = (ІУ.2.39)

Як бачимо з (ІУ.2.39), і г визначалось би просто, якби к було сталою

величиною.

У наш час абсолютно точно доведено, що про єдиний коефіцієнт

рефракції протягом доби не може бути мови. Тільки під час нормальної

стратифікації температури коефіцієнт к можна вважати постійним і рівним

К ~0,14 [27].

Нормальна стратифікація настає вранці, приблизно через годину

після сходу Сонця й під час ясної погоди продовжується біля півгодини,

Ввечері нормальна стратифікація настає десь за 1,5 години до заходу Сонця

й також продовжується півгодини. Отже, нормальна стратифікація під час

антициклонної, ясної погоди продовжується всього біля 1 години на добу.

Під час похмурої погоди ці періоди можуть розширитися й сумарно

складатимуть не більше 3-3,5 години. Нормальна стратифікація повітря

характеризується нормальними вертикальними градієнтами температури.

Під час підйому на 100 м температура падає майже на 1°С. Спостерігач ці

періоди може визначати за майже спокійними зображеннями візирної цілі.

У ці періоди діє нормальна рефракція, яка визначається за формулою

Р_

Тиск Р та температуру Т досить знати наближено. Можна прийняти

Р = 986 мбар (740 мм.рт.ст.); Т = 288°К (І = 15°С). Тоді

= 0,23'10'

'5 (м). (ІУ.2.41)

При цьому (див. формулу (ІУ.2.35)).

/о =к

-г

. (ІУ.2.42)

Перетворимо формулу (ІУ.2.42).

Оскільки

—

= —,то:

5 р

81-8

£„=0,198^$. (ІУ.2.40)

Враховуючи (ІУ.2.41), запишемо:

(ІУ.2.43)