Підручник - Алгебра і початок аналізу 10 клас Нелін Академічний рівень

Подождите немного. Документ загружается.

§ 5. Графіки рівнянь та нерівностей з двома змінними 101

Продовження табл. 13

2. Графіки рівнянь та нерівностей з двома змінними

Означення. Графіком рівняння (нерівності) з двома змінни-

ми х і у називається множина всіх точок координатної площини з коор-

динатами (х; у), де пара чисел (х; у) є розв’язком відповідного рівняння

(нерівності).

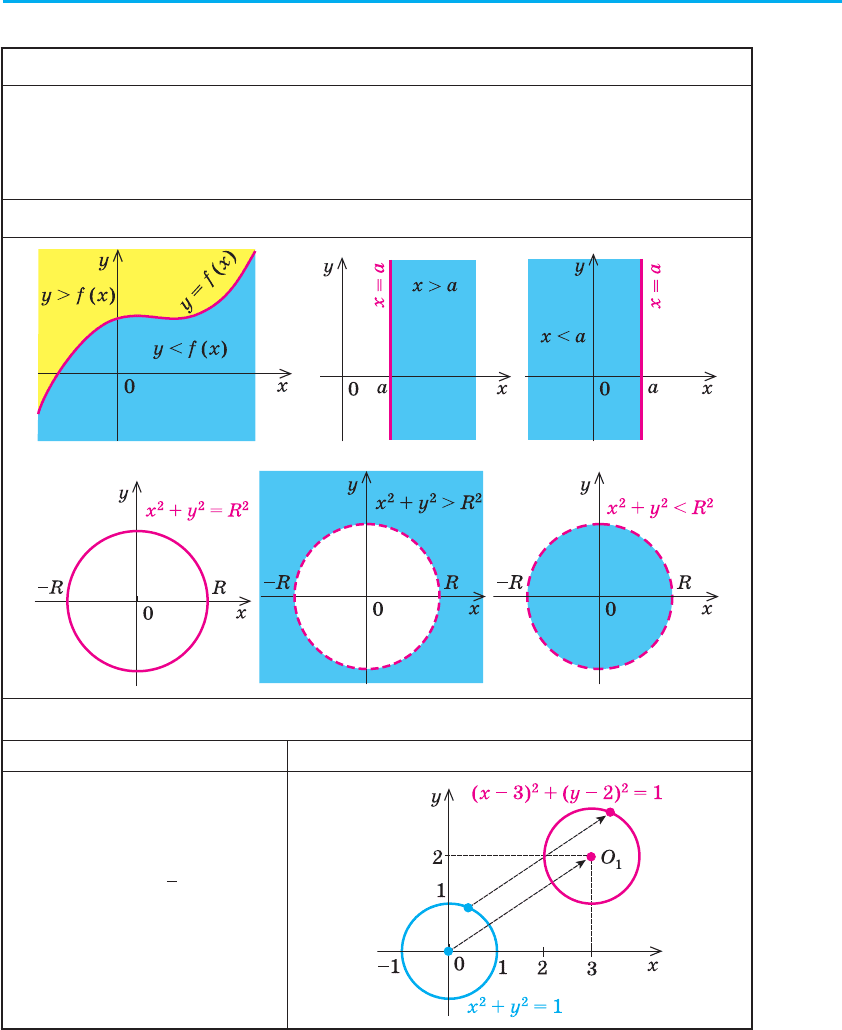
Графіки деяких рівнянь і нерівностей

3. Геометричні перетворення графіка рівняння F (x; y) = 0

Перетворення Приклад

F (x – a; y – b) = 0

Паралельне перенесення

графіка рівняння

F (x; y) = 0

на вектор

nab(; )

102 Розділ 1. ФУНКЦІЇ, РІВНЯННЯ І НЕРІВНОСТІ

Продовження табл. 13

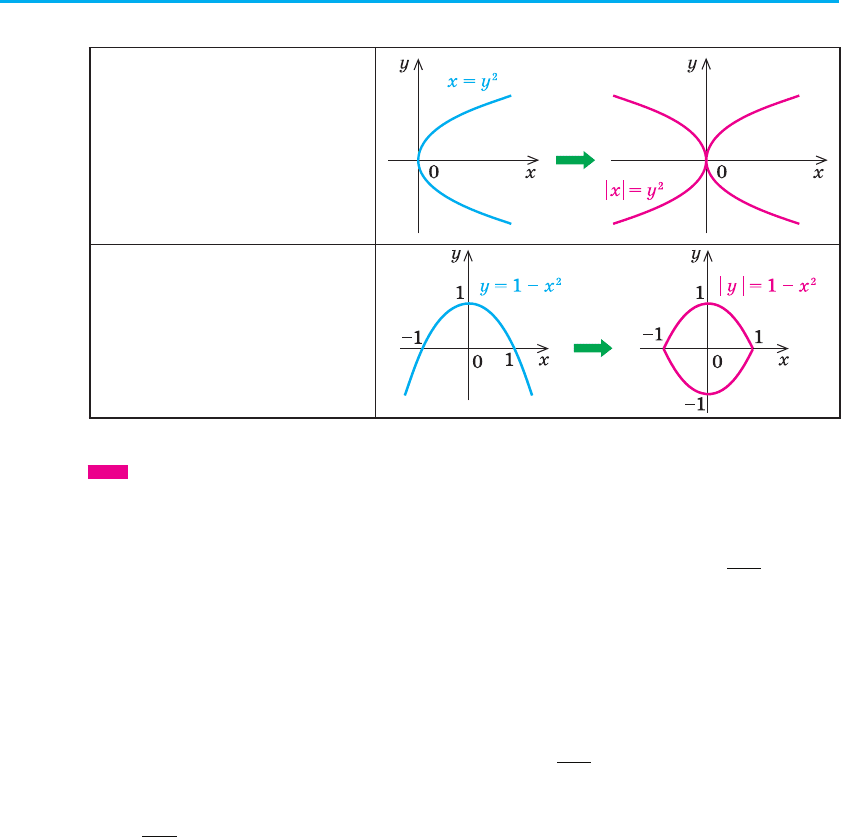
F ( | x |; y) = 0

Частина графіка рівнян-

ня F (х; у) = 0 праворуч від

осі Оy (і на самій осі) за-

лишається без зміни, і ця

сама частина відображу-

ється симетрично відносно

осі Оy.

F (x; | y | ) = 0

Частина графіка рівняння

F (х; у) = 0 вище від осі Ох

(і на самій осі) залишається

без зміни, і ця сама части-

на відображується симе-

трично відносно осі Оx.

Пояснення й обґрунтування

1. Побудова графіків функцій виду y = f (x) + g (x). Якщо відомі гра-

фіки функцій y = f (x) та y = g (x), то можна побудувати орієнтовний вид

графіка функції y = f (x) + g (x), або y = f (x)•g (x), або y

()

. Для

цього достатньо зобразити в одній системі координат графіки функцій

f (x) і g (x), а потім побудувати шуканий графік за точками, виконуючи

для кожного значення x (з області визначення заданої функції) необхід-

ні операції над відрізками (або над довжинами цих відрізків), які зобра-

жають відповідні ординати f (x) і g (x).

Приклад побудови графіка функції виду y = f (x) + g (x) наведено

в таблиці 13, а графіка функції виду y

()

— далі в прикладі 1

(в останньому випадку зручно будувати графіки функцій y = f (x) і

()

не в одній системі координат, а в різних, розміщених так, щоб

їхні осі ординат розташовувалися на одній прямій).

Зауважимо, що такий спосіб побудови графіка функції не завжди

дає можливість виявити всі характерні особливості поведінки графіка

(часто це можна зробити тільки в результаті спеціального дослідження

функції, яке буде розглянуто в 11 класі), але в багатьох випадках наве-

дений спосіб дозволяє отримати певне уявлення про вид графіка заданої

функції.

§ 5. Графіки рівнянь та нерівностей з двома змінними 103

2. Графіки рівнянь та нерівностей з двома змінними. З поняттям гра-

фіка рівняння з двома змінними ви ознайомилися в курсі алгебри. Ана-

логічно вводиться і поняття графіка нерівності з двома змінними. Тому

можна дати спільне означення цих графіків:

Графіком рівняння (нерівності) з двома змінними х і у назива-

ється множина всіх точок координатної площини з координатами

(х; у), де пара чисел (х; у) є розв’язком відповідного рівняння (не-

рівності).

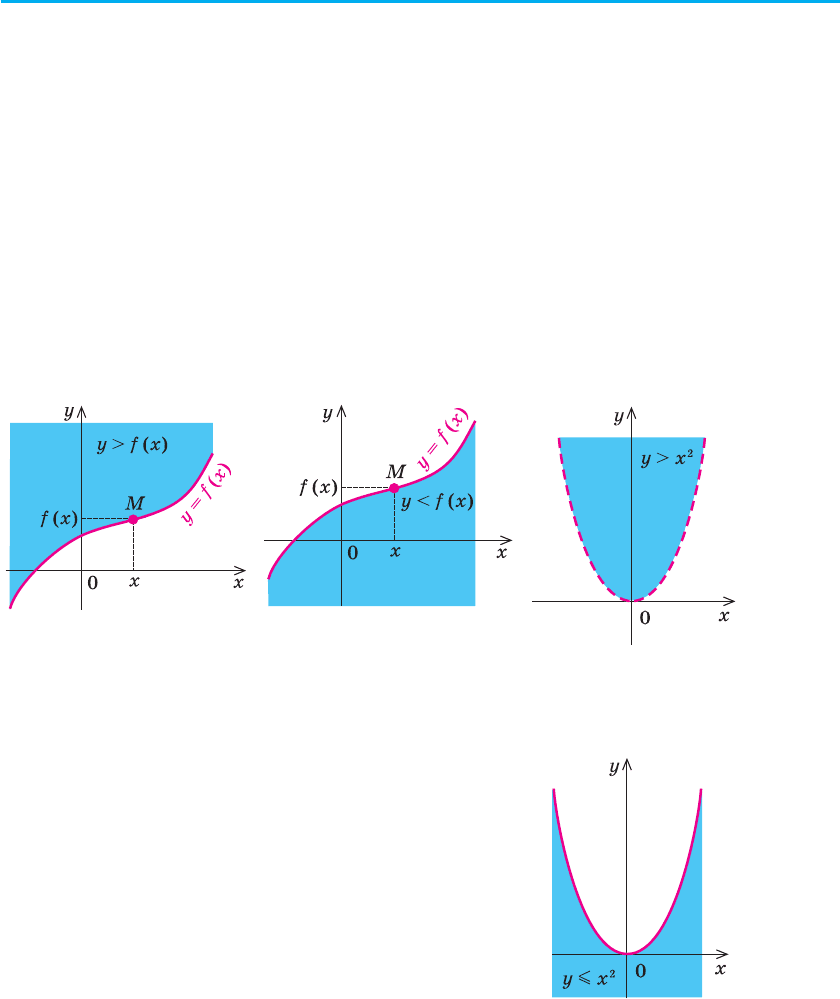
 Для побудови графіка нерівності y > f (x) (чи y < f (x)) достатньо

мати графік функції y = f (x). Дійсно, за означенням графік функції

y = f (x) складається з усіх точок M координатної площини з координа-

тами (x; y) = (x; f (x)). Тоді для кожного значення x точки, координати

яких задовольняють нерівності y > f (x), будуть розташовані вище точ-

ки M (рис. 54, а), а точки, координати яких задовольняють нерівності

y < f (x), будуть розташовані нижче точки M (рис. 54, б). Таким чином,

Рис. 54 Рис. 55

графік нерівності y > f (x) складається з усіх точок координатної

площини, які знаходяться вище від графіка функції y = f (x), а гра-

фік нерівності y < f (x) складається з усіх точок

координатної площини, які знаходяться нижче

від графіка функції y = f (x). 

Наприклад, на рисунку 55 зображено графік

нерівності y > x

, а на рисунку 56 графік нерівності

y m x

. Оскільки точки графіка y = x

не належать

графіку нерівності y > x

, то на першому графіку

парабола y = x

зображена штриховою лінією; але

точки графіка y = x

належать графіку нерівності

y m x

, тому на другому графіку парабола y = x

зо-

бражена суцільною лінією.

Рис. 56

104 Розділ 1. ФУНКЦІЇ, РІВНЯННЯ І НЕРІВНОСТІ

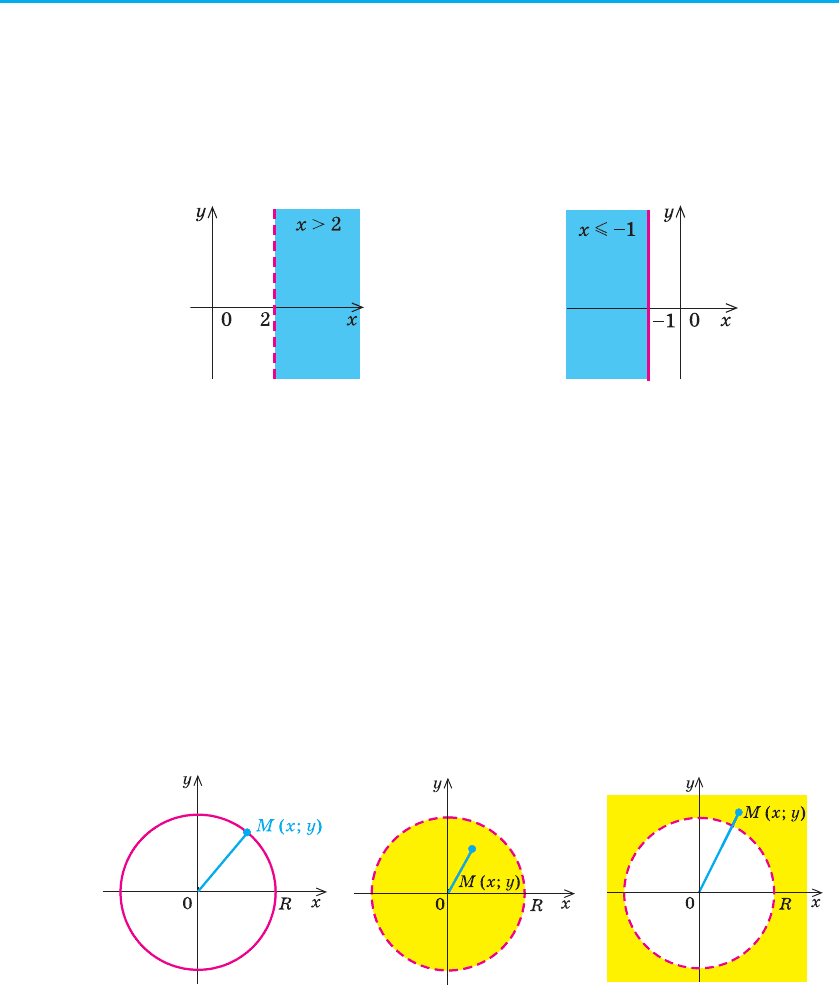
Аналогічно, якщо на координатній площині є пряма x = a, то

графіком нерівності x > a будуть усі точки координатної площини,

які розташовані праворуч від цієї прямої, а графіком нерівності

x < a будуть усі точки координатної площини, які розташовані ліво-

руч від цієї прямої.

Наприклад, на рисунку 57 зображено графік нерівності x > 2, а на

рисунку 58 — графік нерівності x m –1.

Рис. 57 Рис. 58

Зазначимо, що в тому випадку, коли на координатній площині є зо-

браження кола x

+ y

= R

, то

графіком нерівності x

+ y

< R

будуть усі точки координатної

площини, які розташовані всередині кола, а графіком нерівності

+ y

> R

будуть всі точки координатної площини, які розташо-

вані поза колом.

 Дійсно, якщо на координатній площині розглянути точку M (x, y),

то OM

= x

+ y

(точка O — початок координат). Якщо x

+ y

= R

(де R > 0), то OM

= R

, отже, OM = R — точка M лежить на колі

радіуса R із центром у початку координат (рис. 59, а).

Якщо x

+ y

< R

, то OM

< R

, отже, OM < R. Тобто нерівності

+ y

< R

задовольняють координати всіх точок (і тільки цих то-

чок), які розташовані всередині круга, обмеженого колом радіуса R

із центром у початку координат (рис. 59, б).

а б в

Рис. 59

§ 5. Графіки рівнянь та нерівностей з двома змінними 105

Якщо x

+ y

> R

, то OM

> R

, отже, OM > R. Тобто нерівності

+ y

> R

задовольняють координати всіх точок (і тільки цих то-

чок), які знаходяться поза кругом, обмеженим колом радіуса R із

центром у початку координат (рис. 59, в).

Аналогічно, якщо на площині є зображення кола (x – a)

+ (y – b)

= R

, то графіком нерівності (x – a)

+ (y – b)

< R

будуть

усі точки координатної площини, які розташовані всередині кола,

а графіком нерівності (x – a)

+ (y – b)

> R

будуть усі точки коор-

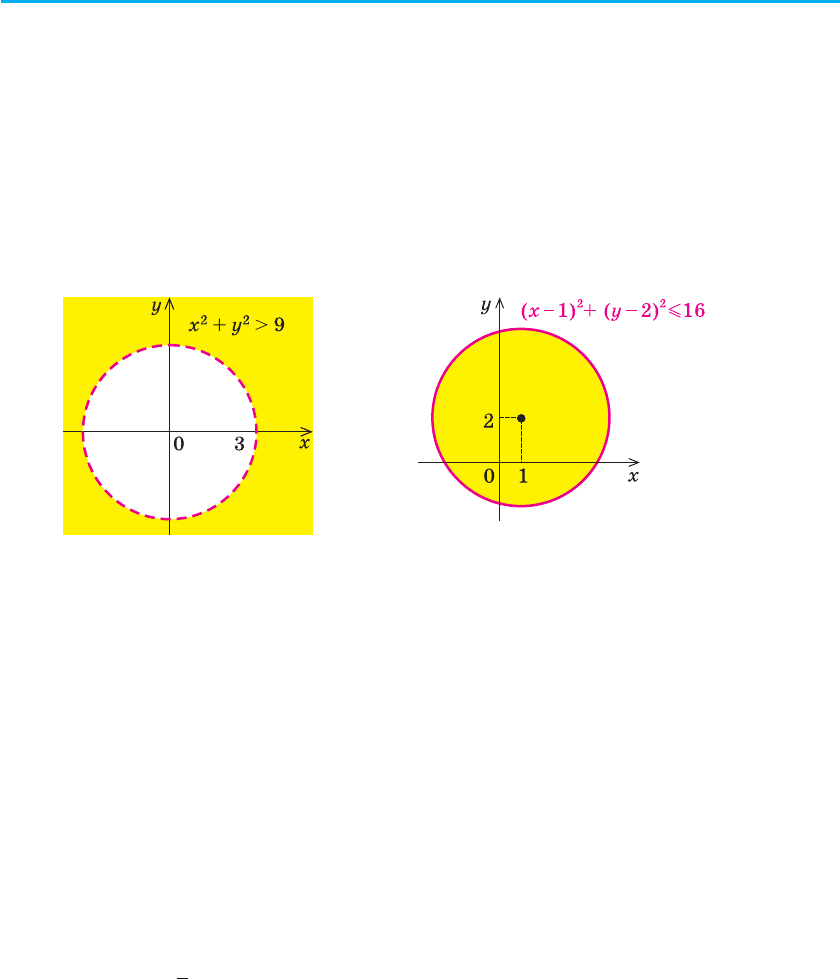
динатної площини, які розташовані поза колом. Наприклад, на ри-

сунку 60 зображено графік нерівності x

+ y

> 9, а на рисунку 61 —

графік нерівності (x – 1)

+ (y – 2)

m 16. 

Рис. 60 Рис. 61

3. Геометричні перетворення графіка рівняння F (x; y) = 0.

 За означенням графік рівняння

F (x; y) = 0 (1)

складається з усіх точок M (x

; y

) координатної площини, коорди-

нати (x

; y

) яких є розв’язками цього рівняння. Це означає, що при

підстановці пари чисел (x

; y

) у задане рівняння воно перетворюєть-

ся на правильну числову рівність, отже, F (x

; y

) = 0 — правильна

рівність.

Розглянемо точку M

+ a; y

+ b). Якщо координати цієї точки

підставити в рівняння

F (x – a; y – b) = 0, (2)

то одержимо рівність F (x

; y

) = 0, яка є правильною. Тому коорди-

нати точки M

є розв’язками рівняння (2), а отже, точка M

нале-

жить графіку рівняння F (x – a; y – b) = 0. Точку M

+ a; y

+ b)

можна одержати з точки M (x

; y

) паралельним перенесенням її

на вектор

nab(; ). Оскільки кожну точку M

графіка рівняння

F (x – a; y – b) = 0 можна одержати з точки M графіка рівняння

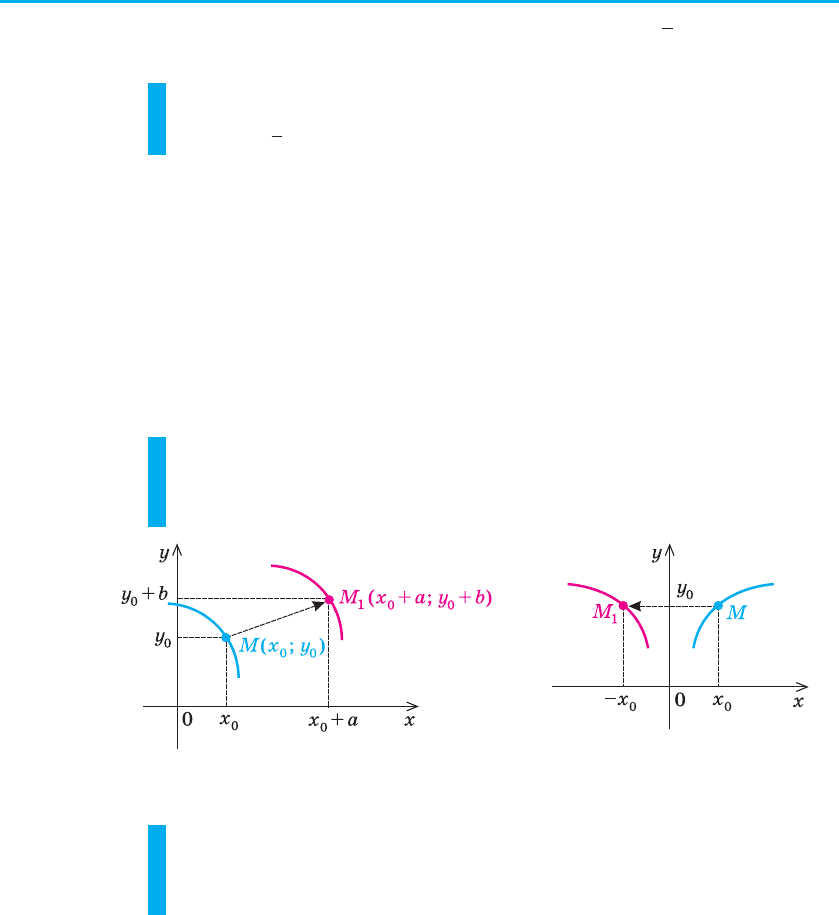
106 Розділ 1. ФУНКЦІЇ, РІВНЯННЯ І НЕРІВНОСТІ

F (x; y) = 0 паралельним перенесенням її на вектор nab(; ) (рис. 62),

то і весь

графік рівняння F (x – a; y – b) = 0 можна одержати з графі-

ка рівняння F (x; y) = 0 паралельним перенесенням його на

вектор

nab(; ). 

 Для обґрунтування зв’язку між графіками F (х; у) = 0 і F (| x |; y) = 0

достатньо помітити, що при х l 0 рівняння F (| x |; y) = 0 збігається

з рівнянням F (х; у) = 0, отже, збігаються і їхні графіки праворуч

від осі Оy і на самій осі. Нехай точка M (x

; y

) (де х

l 0) — одна із

спільних точок цих графіків. Тоді F (x

; y

) = 0 — правильна рівність.

Розглянемо точку M

(–x

; y

). Якщо координати цієї точки підста-

вити в рівняння F (| x |; y) = 0 і врахувати, що х

l 0, то одержимо

рівність F (x

; y

) = 0, яка є правильною. Тому координати точки M

є розв’язками рівняння F (| x |; y) = 0, а отже, точка M

належить

графіку цього рівняння. Ураховуючи, що точки M і M

симетричні

відносно осі Оy (рис. 63),

графік рівняння F ( | x |; y) = 0 можна одержати із графіка рівнян-

ня F (х; у) = 0 так: частину графіка рівняння F (х; у) = 0 праворуч

від осі Оy (і на самій осі) залишити без змін і цю саму частину

відобразити симетрично відносно осі Оy. 

Рис. 62 Рис. 63

Аналогічно можна обґрунтувати, що

для побудови графіка рівняння F (x; | y |) = 0 частину графіка

рівняння F (х; у) = 0 вище від осі Ох (і на самій осі) потрібно

залишити без змін і цю саму частину відобразити симетрич-

но відносно осі Оx.

У таблиці 13 наведено найпростіші приклади використання геоме-

тричних перетворень графіків рівнянь. Указані співвідношення вико-

ристовують у завданнях типу: побудувати графік рівняння чи нерівності

або зобразити на координатній площині множину точок, координати

яких задовольняють заданому рівнянню (нерівностi).

§ 5. Графіки рівнянь та нерівностей з двома змінними 107

Приклади розв’язання завдань

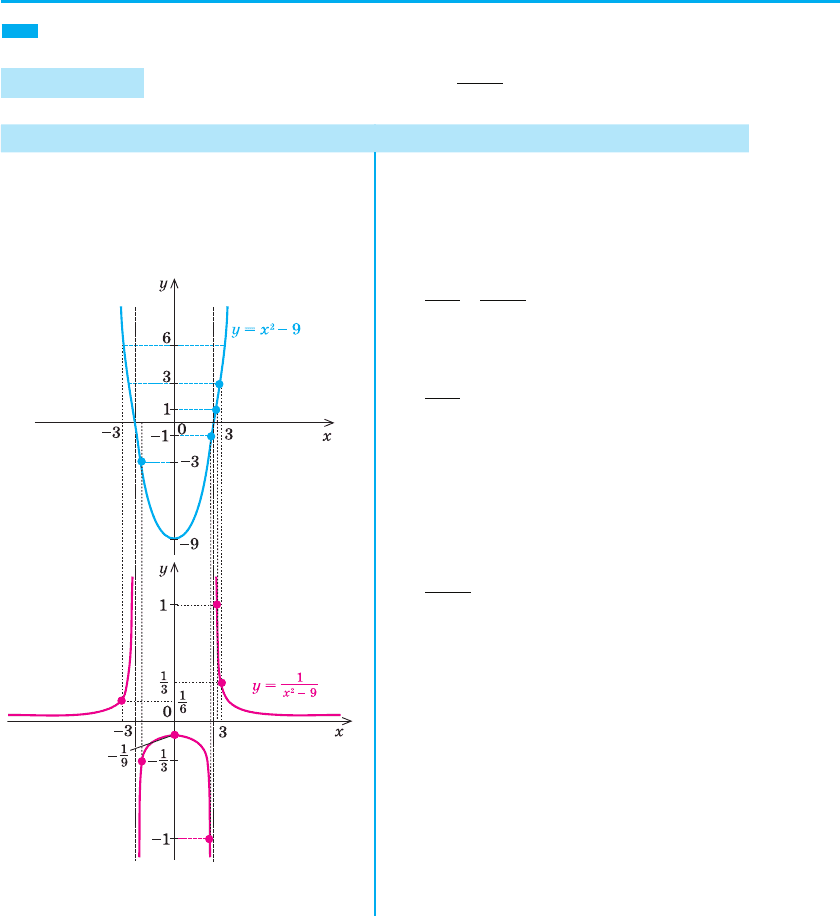
Приклад 1 Побудуйте графік функції

−

Розв’язання Коментар

 x

– 9 = 0 при x = ±3. Тому об-

ласть визначення заданої функ-

ції:

– 9 ≠ 0, тобто x ≠ ±3.



Побудуємо дві системи коорди-

нат так, щоб осі ординат у них були

на одній прямий. У тих точках, де

функція f (x) = x

– 9 дорівнює нулю

(x = ±3), не існує графіка функції

−

()

. Тому проведемо че-

рез ці точки вертикальні прямі, що

не перетинають графік функції

()

. Потім для кожного значен-

ня x поділимо 1 на відповідне

значення ординати f (x) (використо-

вуючи те, що ординати f (x) від-

мічені на верхньому графіку).

На рисунку червоною лінією зобра-

жено результат — графік функції

−

. (Для побудови цього гра-

фіка вибрано різний масштаб по

осях Ох і Оу.)

108 Розділ 1. ФУНКЦІЇ, РІВНЯННЯ І НЕРІВНОСТІ

Приклад 2 Покажіть штриховкою на координатній площині множи-

ну точок, координати яких задовольняють системі

−<







m ,

Розв’язання Коментар

 Задана система рівносильна сис-

темі

m −

>−







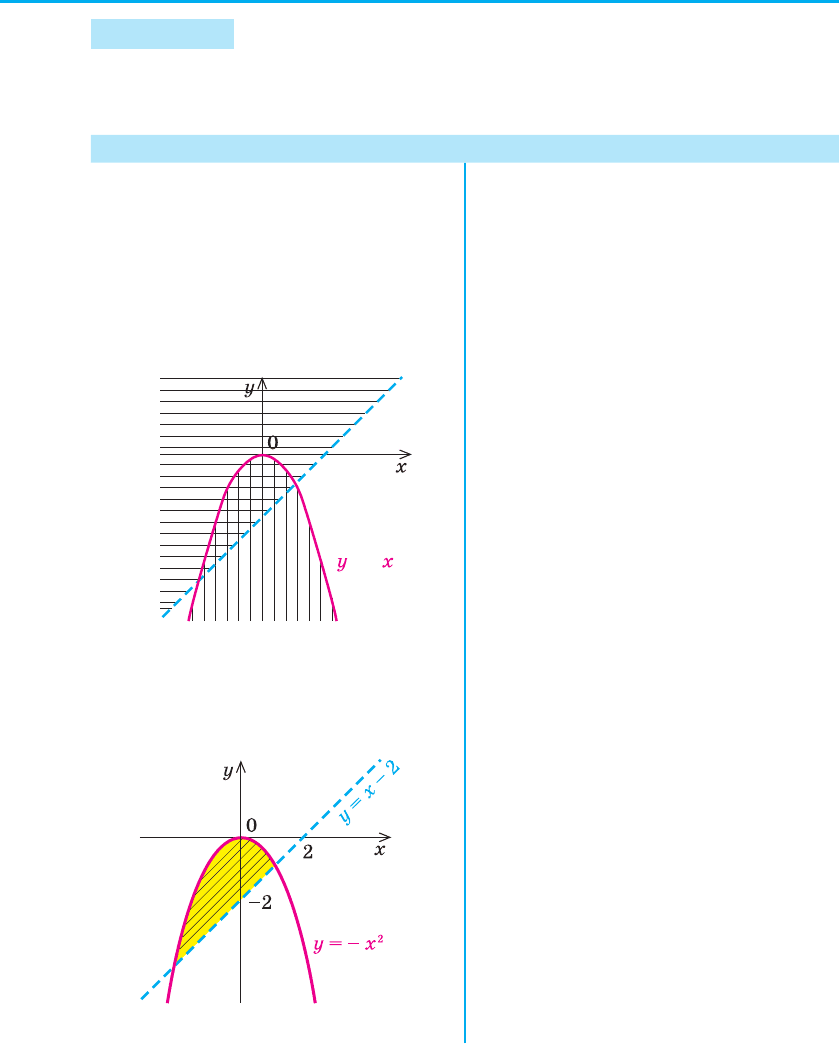
Зобразимо штриховкою графіки

нерівностей системи (першої — вер-

тикальною, другої — горизонтальною):

–

–2

y x= –

Рис. 64

Тоді множина точок, коорди-

нати яких задовольняють системі,

буде такою:

Рис. 65 

Перепишемо задану систему

так, щоб нам було зручно зобра-

жати графіки заданих нерівностей

(тобто запишемо нерівності у вигля-

ді y > f (x) або y < f (x)). Множиною

точок, координати яких задовольня-

ють нерівності y m –x

, є об’єднання

параболи y = –x

і точок коорди-

натної площини, які розташовані

нижче цієї параболи (на рис. 64 ця

множина позначена вертикальною

штриховкою). Множина точок, ко-

ординати яких задовольняють не-

рівності y > x – 2, складається

з точок координатної площини, які

знаходяться вище прямої y = x – 2

(на рисунку ця множина позначена

горизонтальною штриховкою).

Системі нерівностей задовольня-

ють координати тих і тільки тих то-

чок, які належать перетину множин

точок, що задаються кожною з не-

рівностей заданої системи (на ри-

сунку перетину множин відповідає

та область, де штриховки наклалися

одна на одну).

Зауважимо, що в подібних

завданнях можна не виконува-

ти проміжних рисунків, а відразу

штрихувати шукану множину то-

чок координатної площини (вище

прямої y = x – 2 і нижче параболи

y = –x

разом з тією частиною па-

раболи, яка лежить вище прямої;

рис. 65).

§ 5. Графіки рівнянь та нерівностей з двома змінними 109

Приклад 3 Побудуйте графік рівняння | х – у | + 2 | х + у | = х + 6.

Орієнтир

Для спрощення виразу з кількома модулями з двома змінними мож-

на знайти нулі підмодульних виразів (тобто прирівняти їх до нуля) і

розбити область визначення розглядуваного виразу на декілька частин,

у кожній з яких всі модулі розкриваються однозначно.

Використовуючи цей орієнтир, одержуємо план розв’язання прикладу.

Прирівняємо до нуля підмодульні вирази х – у = 0 (звідси у = х)

і х + у = 0 (звідси у = –х). Прямі у = х і у = –х розбивають координатну

площину на чотири області. У кожній із цих областей всі модулі роз-

криваються однозначно, і після перетворення одержаної рівності можна

будувати відповідну частину графіка заданого рівняння.

Розв’язання

 1. Область визначення: х ∈ R, у ∈ R.

2. х – у = 0 при у = х; х + у = 0 при у = –х.

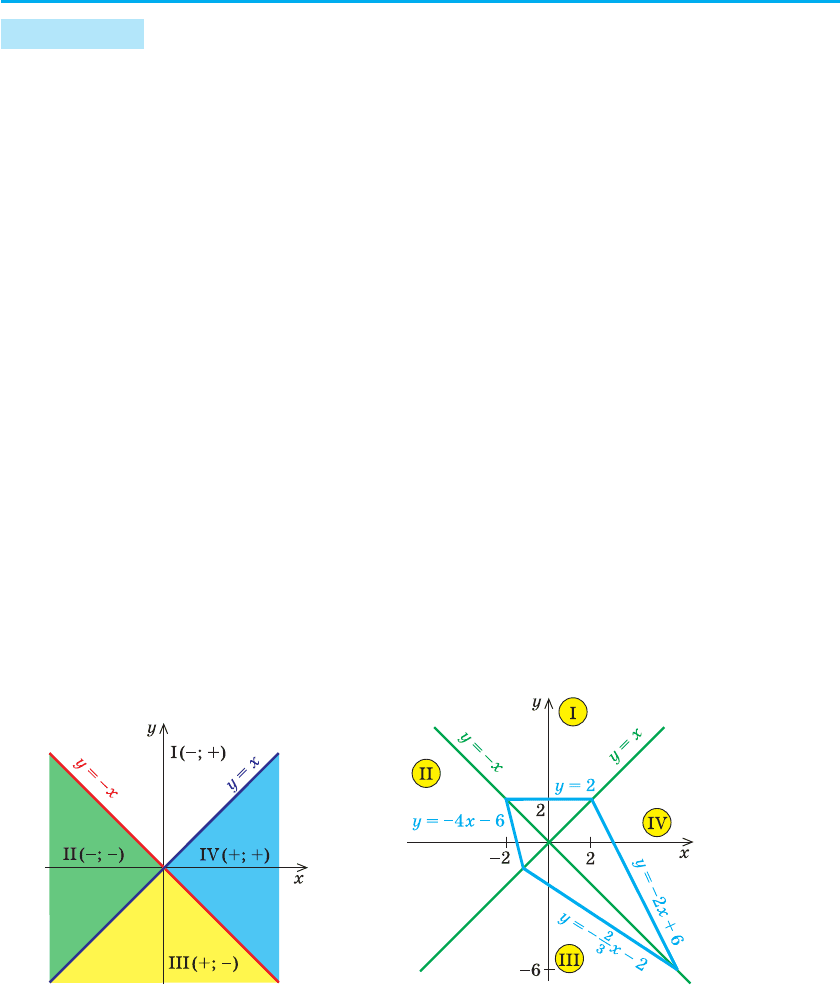
3. Прямі у = х і у = –х розбивають координатну площину на чотири

частини, у кожній з яких позначено знаки першого і другого під-

модульних виразів (рис. 66, а). (Будемо вважати, що кожна область

береться разом із променями, які її обмежують.) Дійсно, якщо точки

розташовані в області І або на її межі, то їхні координати задоволь-

няють системі нерівностей

,−







яку можна записати так:

−







Тоді в області I перший підмодульний вираз є від’ємним,

а другий — додатним, і тому задане рівняння має вигляд: –(х – у) +

+ 2 (х + у) = х + 6. Звідси у = 2. Будуємо частину графіка цієї функ-

ції, що роз міщується в області І (рис. 66, б).

а б

Рис. 66

110 Розділ 1. ФУНКЦІЇ, РІВНЯННЯ І НЕРІВНОСТІ

Аналогічно для точок області II:

,−







тобто

−







Отже, в області ІІ задане рівняння має вигляд: –(х – у) – 2 (х + у) =

= х + 6. Звідси у = –4х – 6. Будуємо частину графіка цієї функції,

що розташовується в області ІI.

Якщо точки розташовані в області III:

,−







тобто

−







із заданого рівняння одержуємо (х – у) – 2 (х + у) = х + 6. Звідси

=− −

Якщо точки лежать в області IV:

,−







тобто

−







із задано-

го рівняння маємо (х – у) + 2 (х + у) = х + 6. Звідси у = –2x + 6.

Остаточний вигляд графіка рівняння наведено на рисунку 66, б. 

Запитання для контролю

Поясніть на прикладах, як можна, маючи графіки функцій y = f (x)

та y = g (x), побудувати ескіз графіка функції y = f (x) + g (x) та

функції

()

2. Що називається графіком рівняння з двома змінними? Що назива-

ється графіком нерівності з двома змінними? Наведіть приклади.

Як, знаючи графік функції y = f (x), побудувати графік нерівності

y > f (x) та нерівності y < f (x)? Наведіть приклади.

Як, знаючи графік рівняння F (x; y) = 0, можна побудувати графік

рівняння F (x – a; y – b) = 0 та рівнянь F ( | x |; y) = 0 і F (x; | y |) = 0?

Наведіть приклади.

5. Обґрунтуйте правила геометричних перетворень графіка рівняння

F (x; y) = 0 для одержання графіків рівнянь F (x – a; y – b) = 0,

F ( | x |; y) = 0, F (x; | y |) = 0.

6. Поясніть на прикладі, як можна знайти на координатній площині

множину точок, координати яких задовольняють системі нерівно-

стей із двома змінними.

Вправи

1. Побудуйте ескіз графіка функції:

; 2) yx

=−

;

3) yx

; 4) yx

=−