Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials
Подождите немного. Документ загружается.


Fundamentals of diffraction
-
-
Real
axis
Figure
2.57.
The relationships between different components of the structure amplitude in a
Friedel pair when all atoms scatter normally (left) and when there are anomalously scattering
atoms in the crystal structure (right).
In
Eq. 2.1 15 the factors
A
and
B
represent, respectively, the real and
imaginary parts of the structure amplitude which are independent of the
anomalous scattering, and
6A"
and
6B"
appear due to the effect introduced
by the presence of the complex component of the anomalous scattering,
Af
".
The combined effect of
6A1'
and
6B"
results in the modification of the
corresponding structure amplitude vectors by
6F(h)"
and
6F(h)11.
This
breaks all equalities in
Eq.
2.1 14 and is illustrated in
Figure
2.57,
right.
Thus, Friedel's law is violated in noncentrosymmetric crystal structures
containing anomalously scattering species.
When the crystal structure is centrosymmetric (Eq. 2.108), Friedel's law
(Eq. 2.1 14) becomes fully valid even in the presence of the anomalously
scattering atoms. This statement is easy to verify and we leave this exercise
to the reader.
2.12.2
Friedel's law and multiplicity factor
Earlier, we considered the effect of lattice symmetry on the multiplicity
factors in powder diffraction only in terms of the number of completely
overlapping equivalent Bragg peaks (section 2.10.3). Because Friedel's law
is violated in non-centrosymmetric structures in the presence of anomalously
scattering chemical elements, the evaluation of multiplicity factors should
also include Eqs. 2.1 14 and 2.115. Thus, the multiplicity factor,
phkl,
may be
comprehensively defined as the number of equivalent reflections
(hkl),
which satisfy Eq. 2.114 in addition to having identical lengths of the

222 Chapter
2
reciprocal lattice vectors calculated using
Eq.
2.37 (or its equivalent for
higher symmetry crystal systems).
Considering an orthorhombic crystal system, the equivalency
relationships established above (section 2.10.3) also satisfy Eq. 2.1
---
14 i.e.
(F(hkl)i= lF(%kl)l
=
~F(h@l
=
jF(hkl)l
=
IF(%@~
=
IF(%@(
=
IF(h kl)1
=
IF(h
k
01
when space group symmetry contains a center of inversion or when
there are no anomalously scattering atoms in the unit cell. The multiplicity
factor in this case is
p
=
8
for all (hkl) reflections where none of the indices
are 0. When the center of inversion is absent and when the anomalous
scattering is considerable, the situation is different. For example, in the space
group P222, the following two sets of structure amplitudes
---
remain identical:
IF(hkl)l
=
(~(h
kl)l
=
IF(%@~
=
(~(hkl)l and IF(h kl)1
=
~F(hkl)l= lF(hkl)(
=
(F(hkl)l but each set of four is different, and the multiplicity factor is reduced
top
=
4
for each of the two groups of points in the reciprocal lattice.
2.12.3 Systematic absences
As noted at the beginning of this section, crystallographic symmetry has
an effect on the structure amplitude, and therefore, it affects the intensities of
Bragg peaks. The presence of translational symmetry causes certain
combinations of Miller indices to become extinct because symmetrical
contributions into Eq. 2.110 result in the cancellation of relevant
trigonometric factors in Eq. 2.107. It is also said that some combinations of
indices are forbidden due to the occurrence of translational symmetry.
2.12.3.1 Lattice centering
Consider a body-centered lattice, in which every atom has a
symmetrically equivalent atom shifted by (112, 112, 112). The two matrices
A
(Eq. 2.109) for every pair of the symmetrically identical atoms are:
The corresponding arguments defined in Eq. 2.1 10 become as follows:
2n(h
+
x),
=
2n(hx
+
ky
+
lz)
2n(h.
x),
=
2n(hx
+
ky
+
lz)
+
n(h
+
k
+
1)

Fundamentals
of
diffraction 223
When these arguments are substituted into the most general equation
(2.107) and the summation is carried over every pair of the symmetrically
equivalent atoms, the resulting sums of the corresponding trigonometric
factors are
cos[2n(hx
+
ky
+
lz)]
+
cos[2n(hx
+
ky
+
lz)
+
n(h
+
k
+
l)]
=
0
sin[2n(hx
+
ky
+
lz)]
+
sin[2n(hx
+
ky
+
lz)
+
n(h
+
k
+
l)]
=
0
cos[2n(hx
+
ky
+
lz)]
+
cos[2n(hx
+
ky
+
lz)
+
n(h
+
k
+
l)]
=
=
2 cos[2n(hx
+
ky
+
lz)]
(2.1 19)
sin[2n(hx
+
ky
+
lz)]
+
sin[2n(hx
+
ky
+
lz)
+
n(h
+
k
+
l)]
=
=
2 sin[2n(hx
+
ky
+
lz)]
when
h
+
k
+
I
=
0,
rt2,
+4,
.
. .
=
2n, where n is an integer.
All prefactors in
Eq.
2.107 (i.e.
g,
t,fo,
Af
', and
Af
")
are identical for the
pairs of the symmetrically equivalent atoms. Hence, Bragg reflections in
which the sums of all Miller indices are odd should have zero structure
amplitude and zero intensity in any body-centered crystal structure. In other
words, they become extinct or absent, and therefore, could not be observed
and are forbidden.
This property, which is introduced by the presence of a translational
symmetry, is called the systematic absence (or the systematic extinction).
Therefore, in a body-centered lattice only Bragg reflections in which the
sums of all Miller indices are even
(i.e.
h
+
k
+
1
=
2n and n
=
+I, k2,
k3,
. .
.)
may have non-zero intensity and be observed. It is worth noting that some
(but not all) of the Bragg reflections with
h
+
k
+
1
=
2n may become extinct
because their intensities are too low to be detected due to other reasons, e.g.
a specific distribution of atoms in the unit cell, which is not predetermined
by symmetry.
Similar analyses may be easily performed for other types of Bravais
lattices, and the resulting relationships between Miller indices are assembled
in Table
2.8.
As a self-exercise try to derive the relationships between Miller

224
Chapter
2
indices of forbidden Bragg peaks for three different types of the base-
centered lattices:
A,
B
and
C.
Table
2.8.
Systematic absences caused by different Bravais lattices.
Bravais
Allowed reflections
lattice
Extinct (forbidden) reflections
P
All None
I
h+k+l= 2n h+k+l= 2n+l
F
h+k
=
2n
and
k+l= 2n
and
h+l= 2na h+k
=
2n+l
or
k+l= 2n+l
or
h+l= 2n+l
A
k+l= 2n
k+l
=
2n+l
B
h+l= 2n h+l= 2n+l
C
h+k
=
2n
h+k
=
2n+l
R~
-h+k+l= 3n
(hexagonal basis)
-h+k+l= 3n+l
and
3n+2
Rc
h-k+l
=
3n
(hexag&al basis)
'
h-k+l= 3n+l
and
3n+2
a
Alternative definition: all indices even
(h=2n
and
k2n
and
1=2n)
or all odd
(h=2n+l
and
k2n+l
and
1=2n+l).
"tandard setting.
Reverse setting.
2.12.3.2
Glide planes
We now consider
a
glide plane, n, perpendicular to the Y-axis. In the
simplest case (i.e. when the plane also intersects the origin of coordinates),
the equivalents of Eqs. 2.1 16 to 2.1 19 become:
2n(h.
x),
=
2n(hx
+
ky
+
lz)
2n(h
.
x),
=
2n(hx
-
ky
+
lz)
+
n(h
+
I)
cos[2n(hx
+
Oy
+
lz)]
+
cos[2n(hx
-
Oy
+
lz)
+
n(h
+
l)]
=
=
0
(2.122)
sin[2n(hx
+
Oy
+
lz)]
+
sin[2n(hx
-
Oy
+
lz)
+
n(h
+
l)]
=
=
0

Fundamentals of diffraction 225
cos[2n(hx
+
Oy
+
lz)]
+
cos[2n(hx
-
Oy
+
lz)
+
n(h
+
l)]
=
=
2
cos[2n(hx
+
lz)]
sin[2n(hx
+
Oy
+
lz)]
+
sin[27c(hx
-
Oy
+
lz)
+
n(h
+
l)]
=
=
2 sin[2n(hx
+
lz)]
when h +I =0, +2,f4,
...
=2n.
Hence, Bragg peaks
(h01)
in which the sum of h and 1 is odd should have
--
-
zero structure amplitude and zero intensity due to the presence of the glide
plane n in this orientation. Only Bragg peaks in which the sum of these
Miller indices is even (i.e. h
+
1
=
2n) may have non-zero intensity and be
observed. We note that the presence of this glide plane only affects Bragg
peaks with
k
=
0 because of the change of the sign of
ky
in
Eq.
2.121. Again,
some (but not all) reflections h01 with h
+
1
=
2n may be absent due to
peculiarities of a crystal structure, not associated with the presence of the
glide plane n, but no peaks with h
+
1
=
2n+l can be observed.
Similar analyses may be performed for other types of glide planes in
different orientations and not necessarily traversing the origin of coordinates
(as an exercise
try
to derive the relationships between Miller indices of the
systematically absent Bragg peaks for a glide plane, a, perpendicular to
Y
and
Z
directions). The relationships between allowed Miller indices for
various glide planes in different orientations are shown in Table
2.9.
Table
2.9.
Combinations of indices, which are allowed by various glide planes
Glide plane Orientationa Reflection type Allowed reflectionsb
a (0 10) h01 h
=
2n
(00
1)
hkO
h
=
2n
(1 10) hhl h
=
2n
b
(100) Okl
k=
2n
(001) hkO k=2n
c
(100) Okl 1=2n
(010) h01 1=2n
(1
10) hhl 1=2n
(1
io)
h hl 1=2n
d Okl k+l
=
4n (k,l
=
2n)
(1 10) hhl 2h+l= 4n
(1
=
2n)
n
(1
00) Okl k+l
=
2n
(010) h01 h+l= 2n
(00
1)
hkO h+k
=
2n
(1 10) hhl
1=2n
a
The orientations are given as the crystallographic indices of the corresponding plane.
All other reflections are forbidden.

226 Chapter
2
2.12.3.3
Screw
axes
Consider a screw axis,
2,,
parallel to the Y-axis. The equivalents of Eqs.
2.1 16 to 2.1 19 when the axis passes through the origin of coordinates are as
follows:
I
and
A,
=
2n(h. x),
=
2n(hx
+
ky
+
lz)
2n(h
.
x),
=
2n(-hx
+
ky
-
lz)
+
nk
cos[2n(Ox
+
ky
+
Oz)]
+
cos[2n(-Ox
+
ky
-
Oz)
+
nk]
=
0
(2.126)
sin[2n(Ox
+
ky
+
Oz)]
+
sin[2n(-Ox
+
ky
-
Oz)
+
nk]
=
0
whenk=fl,f3,f5,
...
=2n+ 1; and
cos[2n(Ox
+
ky
+
Oz)]
+
cos[2n(-Ox
+
ky
-
Oz)
+
zk]
=
2 cos[2nky]
(2.127)
sin[2n(Ox
+
ky
+
Oz)]
+
sin[2.n(-Ox
+
ky
-
Oz)
+
nk]
=
2 sin[2nky]
when k
=
0, f2, f4,
.
..
=
2n.
Hence, Bragg peaks (OM), in which k is odd, should have zero structure
amplitude and zero intensity due to the presence of the 2, axis in this
orientation. Only Bragg peaks in which k is even may have non-zero
intensity and be observed. Similar to glide planes, the presence of screw axes
only affects Bragg peaks with two Miller indices equal to
0 because of the
change of the sign of two terms in Eq. 2.125 (hx and lz in this example).
Corresponding analysis may be performed for other types of screw axes
in different orientations. As an exercise
try
to derive the relationships
between Miller indices of the systematically absent Bragg peaks for a
41
screw axis parallel to the
Z
direction. Again, the result remains identical
whether or not the axis intersects the origin of coordinates. The relationships

Fundamentals of diffraction
between Miller indices of Bragg peaks allowed by various screw axes in
different orientations are shown in
Table
2.10.
Table
2.10.
Combinations of indices, which are allowed by various screw axes.
Screw axis Orientationa Reflection type Allowed reflectionsb
21~42
[
1001 hOO h
=
2n
[0
1
01 OkO
k=
2n
21,42, 63 [OOl] 001 1=2n
41~43
[
1001 1200 h
=
4n
[o
101 OkO k=4n
[OOl] 001 1=4n
31,
32,
62,
64
[OOl] 001 1=3n
61,65 [OOl] 001 1=6n
a
The orientations are given as the crystallographic directions.
All
other reflections are forbidden.
2.12.4
Space groups and systematic absences
As shown in section 2.12.3, the presence of translational symmetry
causes extinctions of certain types of reflections. This property of infinite
symmetry elements finds use in the determination of possible space
group(s)
symmetry from diffraction data by analyzing Miller indices of the observed
Bragg peaks. It is worth noting that only infinite symmetry elements cause
systematic absences, and therefore, may be detected
fiom this analysis.
Finite symmetry elements, such as simple rotation and inversion axes, mirror
plane and center of inversion, produce no systematic absences and therefore,
are not distinguishable using this approach.
As is often the case in diffraction analysis, when the space group
symmetry is known, it is quite easy to predict which types of reflections can
and which cannot be observed. For example, when the space group
symmetry is Pnma, only the following types of Bragg peaks may have non-
zero intensity (as established by analyzing Table
2.8
to Table
2.10):
hkl: any (primitive Bravais lattice)
hkO: h
=
2n (glide plane a
I
Z)
h01: any (mirror plane m
I
Y)
Okl: k+l
=
2n (glide plane
n
I
X)
hOO: h
=
2n (derivative of the glide plane a
I
Z
because k
=
0)
OkO: k
=
2n (derivative of the glide plane n
I
X
because 1
=
0)
001: 1
=
2n (derivative of the glide plane n
I
Xbecause k
=
0)
When the space group symmetry is unknown, .i.e. when reflection
conditions are analyzed from diffraction data, the answer may not be unique.
For example, the combination of systematic absences listed above also

228 Chapter 2
corresponds to a different space group symmetry, Pn2,a (as an exercise,
please verify that this space group symmetry produces exactly the same
combination of the allowed Miller indices of Bragg reflections) and
therefore, the two space groups are unrecognizable from a simple analysis of
the present Bragg peaks.
All space groups that produce identical combinations of systematic
absences are combined into the so-called diffraction groups. For example,
space groups
P31c and ~Slc, result in the same allowed reflection
conditions: 1
=
2n
for both Okl and 001 type reflections. They belong to the
trigonal diffraction group P--c. The three hexagonal space groups symmetry
-
PZ~C, P63mc and P63/mmc
-
also belong to the P--c diffraction group, but
the crystal system is hexagonal. When powder diffraction data are used to
analyze systematic absences, these two diffraction groups cannot be
distinguished from one another, which occurs due to the same symmetry of
shapes of both the trigonal and hexagonal unit cells. The two are discernible
using diffraction data from a single crystal, where the three-fold rotation axis
is different from the six-fold rotation axis. In powder diffraction, however,
Bragg reflections with different intensity in the trigonal crystal system, such
as hkl and khl, are exactly overlapped and, therefore, cannot be distinguished
from each other.
Nonetheless, analysis of the systematic absences (the complete list is
found in Table 2.12 to Table 2.17) usually allows one to narrow the choice
of space group symmetry to just a few possibilities, and the actual symmetry
of the material is usually established in the process of the complete
determination of its crystal structure. Especially when powder diffraction
data are used, it only makes sense to analyze low angle Bragg peaks to
minimize potential influence of the nearly completely overlapped reflections
with indices not related by symmetry.
An
example of the space group
determination is shown in Table 2.11.
This powder diffraction pattern was indexed in the monoclinic crystal
system with
a
=
9.264 A, b
=
9.728 A,
c
=
9.905 A,
=
106.08". All
observed Bragg peaks have even sums h
+
k, which clearly points to a base-
centered lattice C. The first four columns in Table 2.11 contain Miller
indices and Bragg angles 28, calculated assuming base-centered lattice C
without applying any other conditions, i.e. as in the space group C2lm. The
next two columns list Bragg angles and integrated intensities of the observed
peaks that correspond to the calculated Bragg angles.
As follows from Table 2.12, there are only two possible diffraction
groups for the monoclinic C-centered lattice. The second diffraction group,
C
1
c
1,
differs from the first one, C 1
-
1, by the presence of h01 reflections only
with even 1. As is easy to see from Table 2.11, none of the Bragg peaks h01
with 1
=
2n
+
1 is observed, or in other words, the allowed reflections
condition is 1
=
2n for h01 (these are shown in bold). Other conditions are
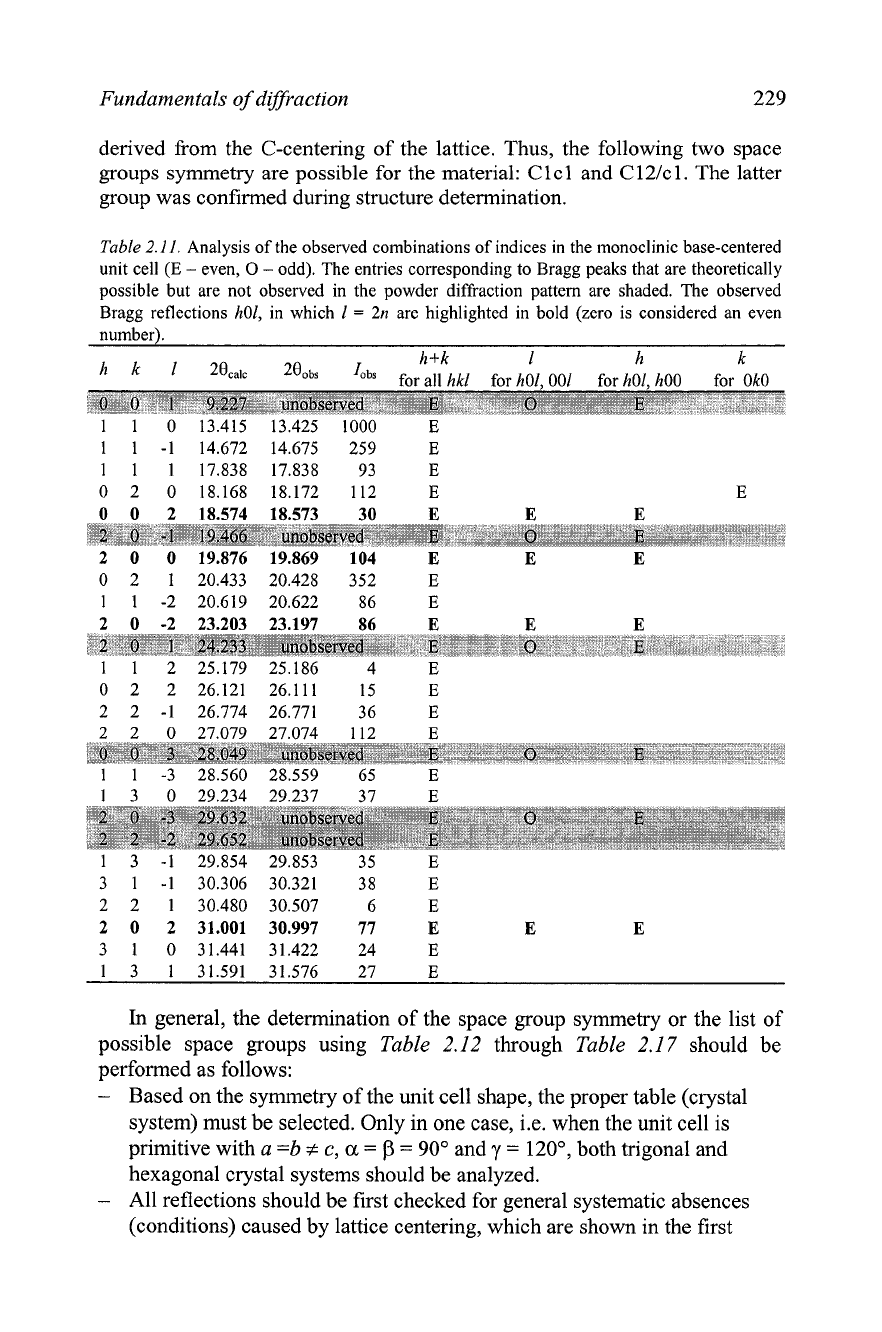
Fundamentals of diffraction
229
derived from the C-centering of the lattice. Thus, the following two space
groups symmetry are possible for the material: C
1
cl and
C
12Ic 1. The latter
group was confirmed during structure determination.
Table 2.1
I.
Analysis of the observed combinations of indices in the monoclinic base-centered
unit cell
(E
-
even,
0
-
odd). The entries corresponding to Bragg peaks that are theoretically
possible but are not observed in the powder diffraction pattern are shaded. The observed
Bragg reflections
h01,
in which
1
=
2n
are highlighted in bold (zero is considered an even
number).
h+k
1
h k
'
28ca1c
280b"0bs
for all
hkl
for
hOl OOl
for
hO1 hOO
for
OkO
1 1
0
13.415 13.425
1000
E
In
general, the determination of the space group symmetry or the list of
possible space groups using
Table
2.12
through
Table
2.1
7
should be
performed as follows:
Based on the symmetry of the unit cell shape, the proper table (crystal
system) must be selected. Only in one case, i.e. when the unit cell is
primitive with
a =b
#
c,
a
=
f!
=
90•‹
and
y
=
120•‹,
both trigonal and
hexagonal crystal systems should be analyzed.
All reflections should be first checked for general systematic absences
(conditions) caused by lattice centering, which are shown in the first

230
Chapter
2
column in each table. This should narrow the list of possible space
groups.
-
Subsequently, move to the next column in the corresponding table.
Identify reflections that belong to a specified combination of Miller
indices listed in the column header and analyze whether or not the
extinction conditions are met. This should further narrow the list of
possible space groups.
-
The last step should be repeated for all columns under the general header
"Reflection conditions". When finished, the list should be narrowed to a
single line, i.e. the corresponding diffraction group should be found for
the known symmetry of the unit cell shape.
-
In the case of monoclinic and orthorhombic crystal systems, it may be
necessary to transform the unit cell in order to achieve a standard setting
of the space group symmetry. The space groups in standard settings are
shown in the corresponding tables in bold. Usually only a permutation of
the coordinate axes is needed but in some cases in the monoclinic crystal
system, such as I-centering or the presence of the glide plane n, a more
complex transformation of the unit cell vectors may be required. If
necessary, the International Tables for Crystallography (vol. A) should be
used as a reference on how to perform a transformation of unit cell
vectors properly.
In
Table
2.12 to
Table
2.17, reflection conditions as determined by the
presence of translational symmetry are listed for all crystal systems, except
triclinic. The latter has no translational symmetry and therefore, the two
possible space groups symmetry,
P1
and
pi,
belong to the same diffraction
class,
PI.
If a cell showing reflection conditions is empty, there are no
restrictions imposed on Miller indices and any combination of them is
allowed. Unless noted otherwise, the corresponding symbol(s) or
expression(s) present in the cell indicate that the index or the combination is
even. Monoclinic and orthorhombic space groups in standard settings are
shown in
bold;
trigonal, hexagonal, tetragonal and cubic space groups are
only shown in standard setting. Space groups with unique reflection
conditions (i.e. those, which are uniquely determined from the systematic
absences) are
f@da
for a standard setting. Superscripts indicate space
group number as listed in the International Tables for Crystallography, vol.
A. The following abbreviations are employed to specify allowed
combinations of indices due to lattice centering:
