Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffraction

25 1

where the symbol

also means "probably equal" and the probability of this

relationship for the phase

is defined as:'

where

is Bessel function, and

k,,,.

2~-''~

IE,

E,. E,-,,.

order to generate phase angles using any of the two Sayre equations

(2.143 or 2.146) some reflections with known phases are needed, since both

equations define one phase from two others. There are several sources of

reflection phases at this stage. First, certain phase angles may be set at

arbitrary values to fix the origin and in the case of non-centrosymmetric

structures, one additional phase with an arbitrary value is needed to fix the

enantiomorph. Second, phase angles of several strong reflections are selected

for permutations. For example in the centrosyrnmetric case, a total of four

reflections would have

24 possible combinations of signs resulting in 16

different sets of possible phase angles.

For each permutation, the phases of all other reflections are generated

using

Sayre equations. Thus, direct methods always result in more than one

array of phases, and the problem is reduced to selecting the correct solution,

if one exists. Several different figures merit andlor their combinations have

been developed and are used to evaluate the probability and the relationships

between phases. Thus, the solutions are sorted according to their probability

from the highest to the lowest. Then each solution is analyzed and

evaluated starting from the one that is most probable.

Usually each reflection forms more than one triplet and each of the

triplets may be used for phase determination (estimation).

order to employ

all triplets and thus, obtain the best agreement between phase angles that

result from different triplets, Karle and

Hauptrnan2 introduced a general

expression for phase determination from triplets. This relationship is known

today as the tangent formula:

Cochran, Relations between the phases of structure factors, Acta Cryst.

8,473

(1955).

J. Karle and H. Hauptman,

theory of phase determination for the four types of non-

centrosymmetric space groups, Acta Cryst.

635 (1956). Jerome Karle, US

crystallographer, and Herbert

Hauptman, US mathematician, laid a foundation towards

the development of modern direct phase determination techniques. They won 1985 Nobel

Prize in Chemistry "for their outstanding achievements in the development of direct

methods for the determination of crystal structures"

http://m.nobel.se/

chemistry/laureates/1985/.

252

Chapter

where the sums include all triplets, in which the reflection in question,

involved.

Finally, the generated phase angles are used in a forward Fourier

transformation combined with the normalized structure amplitudes

Ejkl

and the resulting density distribution is called the E-map. It is quite similar

to a conventional Fourier map representing electron density but E-maps are

usually sharper because the normalized structure amplitudes,

Ejkl,

are

corrected for the effects of atomic scattering and thermal displacements.

generic algorithm of employing direct methods to structure solution

may be summarized in the following steps:

Observed structure amplitudes are scaled and normalized structure

amplitudes are calculated using Eq.

2.141.

Reflections with large

normalized structure amplitudes (a standard cut-off is

Ejkl

Emin =1.2)

are selected for phase determination and refinement.

Reflections to fix the origin and the enantiomorph (if needed) are

selected. There are special requirements on the combinations of indices

of these reflections, which are established by space group symmetry.

Several of the strongest reflections (those that have the largest

Ejkl)

are

chosen for phase permutations.

addition to being the strongest, these

reflections should have combinations of indices that result in as many

triplets as possible with all reflections selected in step

Phases are assigned to all, or as many as possible, reflections selected in

step

using Sayre equations (Eq.

2.143

2.146)

and the probability

relationships (Eq.

2.144

2.147).

The best possible agreement between phases is obtained by using a least

squares refinement in combination with the tangent formula (Eq.

2.148).

Figures of merit are calculated and the resultant sets of phase angles are

sorted fiom the most probable to the least probable solution.

E-map (Eq.

2.149)

is computed for the most probable solution. The peaks

are located on the map and a partial or complete model of the crystal

structure is created.

The obtained model of the crystal structure is analyzed with respect to

common chemical and crystallographic sense

are all bond distances,

Fundamentals

diffraction

angles, coordination polyhedra, etc. reasonable? If yes, move to step

no, go to step

using the next best solution.

The model of the crystal structure is verified and completed by

computing phases for all available (conventional) structure amplitudes

using the current structural model (Eq. 2.105) and successive calculation

of Fourier (Eq. 2.133)

and/or difference Fourier maps (Eq. 2.135). Once

all atoms are located, the complete structure is refined using least squares

technique against all available diffraction data.

10. If no solution is found, step 2 should be repeated with different

parameters and

lists(s) of reflections in the starting sets. It may be

necessary to expand or reduce the list of reflections under consideration

by changing the cut-off value of

Emin

from a standard value of 1.2.

2.14.3

Structure solution from powder diffraction data

Solving the crystal structure using either heavy atom or direct techniques

does not always work in a straightforward fashion even when the well-

resolved and highly accurate diffraction data from a single crystal are

available. The complicating factor in powder diffraction is borne by the

intrinsic overlap of multiple Bragg peaks. The latter may become especially

severe when the unit cell volume and complexity of the structure increase.

Thus, there is a fundamental difference between the accuracy of structure

amplitudes obtained from single crystal and powder diffraction data. The

former are always resolved,

i.e. there is only one combination of indices,

hkl,

per Bragg peak, whereas in the latter some reflections may be fully or

partially overlapped. The intensities of individual reflections

hkl

may still be

recovered from powder diffraction data but their accuracy is critically

dependent on both the degree of the overlap and the quality of the pattern.

Obviously, the absolute overlapping of some reflections makes it impossible

to obtain the individual intensities regardless of the quality of data, and only

the combined total intensity is known

(e.g. reflections 431 and 051 in both the

cubic and tetragonal crystal systems).

As established above, individual intensities (or structure amplitudes) of

Bragg reflections are needed in order to solve the crystal structure using

direct or Patterson methods.

the first case, accurate normalized structure

amplitudes are required to generate phase angles and to evaluate their

probabilities. In the second case, accurate structure amplitudes result in the

higher accuracy and resolution on the Patterson map.

Thus, when reflections overlap to a degree when the individual intensities

can no longer be considered reliable, they may be dealt with using two

different approaches:

254

Chapter

the first, reflections with low accuracy in individual intensities (those

that are completely or nearly completely overlapped) are simply

discarded. This works best when direct methods are used for the structure

solution because substantial errors even in some of the normalized

structure amplitudes may affect phase angles of many other reflections.

the second approach, the total intensity of the diffraction peak is

equally divided among the individual reflections, so that

It,,1

XIi.

Yet

another approach in a "blind" division is to account for the multiplicity

factors of different Bragg reflections, so that

Ito,l

XmiIi,

where

is the

multiplicity factor of the

ith

reflection, which depends on symmetry and

combination of indices (see sections 2.10.3 and 2.12.2). No obvious

preference can be given to any method of intensity division, as each of

them is quite arbitrary. This way of handling the overlapped intensities,

instead of simply discarding them is most beneficial in the Patterson

method.

Even when the crystal structure is partially solved, the individual

intensities are still needed to complete the structure by means of calculating

Fourier or difference Fourier maps. Obviously, the result of Fourier

transformations is affected by the accuracy in the absolute values of the

structure amplitudes in addition to the precision of their phase angles (Eqs.

2.133 and

2.135)' Considering fully overlapped Bragg reflections, the

situation with prorating individual intensities becomes different when

compared to the state when the crystal structure is completely unknown: at

this point, the calculated intensities of all individual reflections are known

with the accuracy of the current structural model. These calculated

intensities may be (and usually are) used to divide the total intensity of the

peak between all overlapped reflections proportionally to their calculated

intensities (see Eq.

6.7

in Chapter

6).

The division of intensities of the overlapped Bragg reflections is only

critical when they are needed to calculate Patterson-, Fourier- or E-map(s).

There is no need in their separation during a least squares refinement of

structural parameters because each point of the diffraction profile is simply

taken as a sum of contributions from multiple Bragg

reflection^.^

We conclude this chapter right where we began by repeating the

following statement: "The diffraction pattern of a crystal is a transformation

of an ordered atomic structure into a reciprocal space rather than a direct

image of the former, and the three-dimensional distribution of atoms in a

It turns out that precisely known phase angles are more critical in determining coordinates

of atoms in the unit cell than the corresponding absolute values of individual structure

factors.

The least squares refinement of structural parameters employing full profile powder

diffraction data is discussed in Chapter

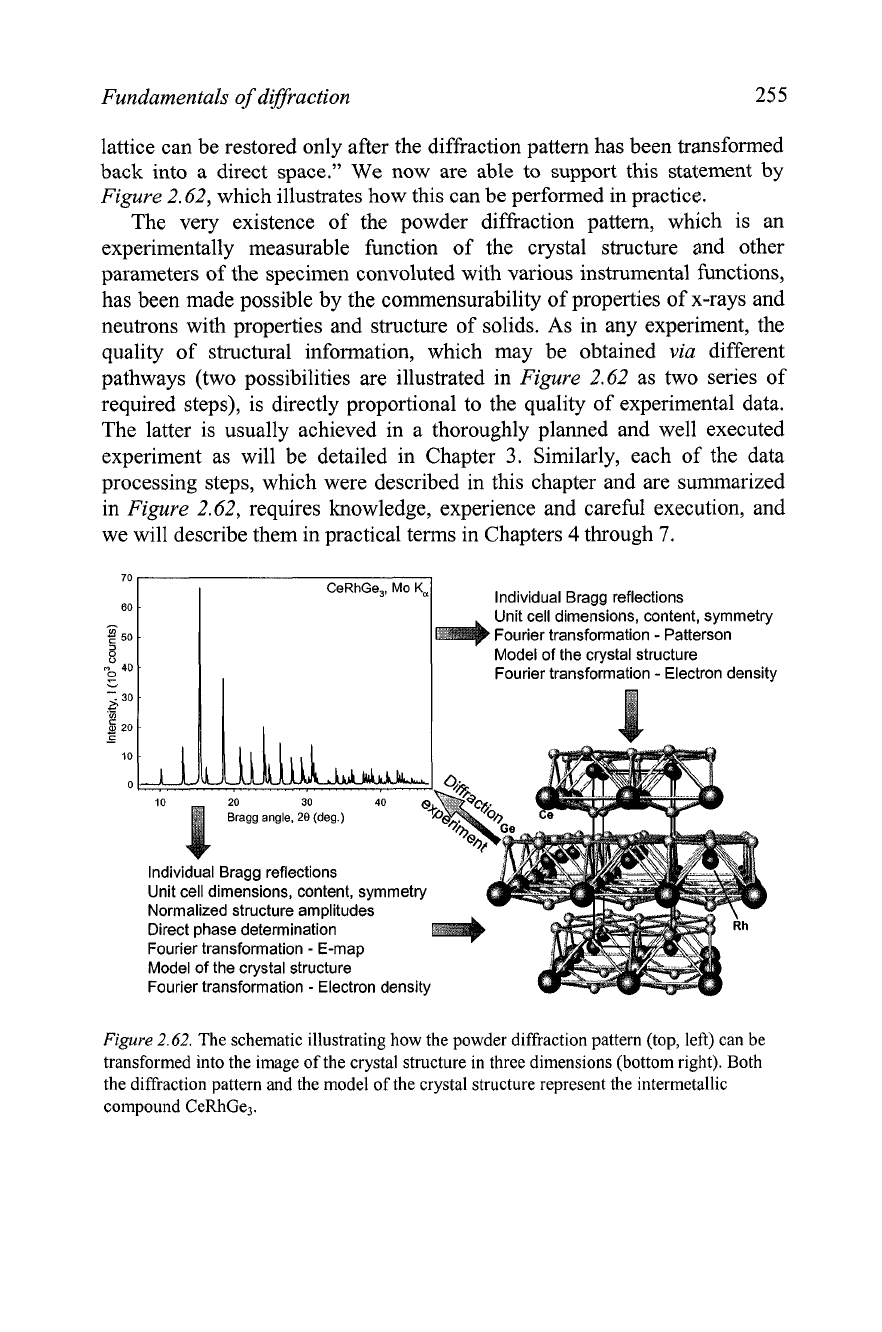
Fundamentals of diffraction

255

lattice can be restored only after the diffraction pattern has been transformed

back into a direct space." We now are able to support this statement by

Figure

2.62, which illustrates how this can be performed in practice.

The very existence of the powder diffraction pattern, which is an

experimentally measurable function of the crystal structure and other

parameters of the specimen convoluted with various instrumental functions,

has been made possible by the commensurability of properties of x-rays and

neutrons with properties and structure of solids. As in any experiment, the

quality of structural information, which may be obtained

via

different

pathways (two possibilities are illustrated

Figure

2.62 as two series of

required steps), is directly proportional to the quality of experimental data.

The latter is usually achieved in a thoroughly planned and well executed

experiment as will be detailed in Chapter

Similarly, each of the data

processing steps, which were described in this chapter and are summarized

Figure

2.62, requires knowledge, experience and careful execution, and

we will describe them in practical terms in Chapters 4 through

CeRhGe,,

Individual Bragg reflections

Unit cell dimensions, content, symmetry

Fourier transformation

Patterson

Model of the crystal structure

Fourier transformation

Electron density

Bragg angle,

(deg.)

Individual Bragg reflections

Unit cell dimensions, content, symmetry

Normalized structure amplitudes

Direct phase determination

Fourier transformation

E-map

Model of the crystal structure

Fourier transformation

Electron density

Figure

2.62.

The schematic illustrating how the powder diffraction pattern (top, left) can be

transformed into the image of the crystal structure in three dimensions (bottom right). Both

the diffraction pattern and the model of the crystal structure represent the intermetallic

compound CeRhGe,.

256

Chapter

2.15

Additional reading

1. International Tables for Crystallography, vol. A, 5th revised edition, Theo

Hahn, Ed., Published for the International Union of Crystallography by

Kluwer Academic Publishers, Boston/Dordrecht/London (2002); vol. B,

Shmueli, Ed., Published for the International Union of

Crystallography by Kluwer Academic Publishers, Boston/Dordrecht/

London (2001); vol.

A.J.C. Wilson and E. Prince, Eds., Published for

the International Union of Crystallography by Kluwer Academic

Publishers, BostodDordrecht/London (1999).

2. International Tables for Crystallography. Brief teaching edition of

volume A. Fourth, revised and enlarged edition. Theo Han, Ed., Kluwer

Academic Publishers, Boston/Dordrecht/London

996).

3. R.B. Neder and Th. Proffen, Teaching diffraction with the aid of

computer simulations, J. Appl. Cryst. 29, 727 (1996); also see Th.

Proffen and R.B. Neder. Interactive tutorial about diffraction on the Web

at http://www.pa.msu.edu/-proffedteaching/teaching.html.

P. A. Heiney. High resolution x-ray diffraction. Physics department and

laboratory for research on the structure of matter. University of

Pennsylvania.

http://dept.physics.upenn.edu/-heiney/talks/hires/hires.h~l

5. Electron diffraction techniques. Vol. 1,2. J. Cowley, Ed., Oxford

University Press. Oxford, New York (1 992)

6. D.K. Bowen and B.K. Tanner. High resolution x-ray diffractometry and

topography. Taylor

Francis. London, Bristol, PA (1998).

7. Modern powder diffraction. D.L Bish and J.E. Post, Eds. Reviews in

Mineralogy, Vol.

20.

Mineralogical Society of America, Washington, DC

(1989).

8. R. Jenkins and R.L. Snyder. Introduction to x-ray powder diffractometry.

John Wiley

Sons, New York (1996).

9. W. Clegg, Synchrotron chemical crystallography. J. Chem. Soc., Dalton

Trans. 19,3223 (2000).

Fundamentals of diffraction

257

10.1. Als-Nielsen and D. McMorrow, Elements of modem x-ray physics,

John Wiley

Sons, New York, (2001).

1 1. P. Coppens, X-ray charge densities and chemical bonding. IUCr Texts on

Crystallography 4, Oxford University Press, Oxford, New York (1 997).

12. V.G. Tsirelson and R.P. Ozerov, Electron density and bonding in

crystals: principles, theory and x-ray diffraction experiments in solid state

physics and chemistry, Institute of Physics, Bristol,

(1996).

13. C. Giacovazzo, Direct phasing in crystallography: fundamentals and

applications. IUCr monographs on crystallography 8, Oxford University

Press, Oxford, New York (1

998).

14. T.M. Sabine, The flow of radiation in a polycrystalline material, in: The

Rietveld method. IUCr monographs on crystallography 5, R.A. Young,

Ed., Oxford University Press, Oxford, New York (1993).

15.

Suortti, Bragg reflection profile shape in x-ray powder diffraction

patterns, in: The Rietveld method. IUCr monographs on crystallography

5, R.A. Young, Ed., Oxford University Press, Oxford, New York (1993).

16.R. Delhez, T.H. de Keijser,

J.I.

Langford,

Louer, E.J. Mittemeijer, and

E.J.

Sonneveld, Crystal imperfection broadening and peak shape in the

Rietveld method, in: The Rietveld method. IUCr monographs on

crystallography

R.A. Young, Ed., Oxford University Press, Oxford,

New York (1993).

Chapter

2.16

Problems

Answers to all problems listed below are located in the file Chapter-2-

Problems-Solutions.pdf on the CD accompanying this book.

1. A powder diffractometer in your laboratory is equipped with a sealed x-

ray tube, which has Cr anode. You need to design a P-filter to ensure that

the intensity of the

KP spectral line is less than 0.5% of the intensity of

the Kal part in the characteristic spectrum. Calculate the needed

thickness of a foil made from the most appropriate metal (which one?)

and by how much the intensity of

Ka, and KP lines will be reduced after

filtering.

2. There are 25 plates in a Soller slit. Axial size of the incident beam when

it exits the slit is 12 mm. Calculate the length of the plates along the x-ray

beam

(I)

if the slit results in the axial divergence of the beam,

2.5".

Neglect the thickness of the plates.

A crystal monochromator is made form high quality pyrolitic graphite

(space group P(i3/rnmc,

2.464, c

6.7 1 1

A).

Assume that this crystal

is used to suppress the Ka2 spectral line of Cu Ka radiation by using the

reflection from (002) planes and that the crystal is cleaved parallel to the

(001) plane. Estimate the linear separation

(6,

in mm) between the

centers of two peaks (Kal and Ka2) at 200

rnrn

distance after the

reflection from the crystal. Assuming that the crystal is nearly ideal

calculate angle

which the incident beam should form with the surface

of the crystal for best result.

4. Vanadium oxide,

V203, crystallizes in the space group symmetry R3c

with lattice parameters a

4.954

and c

14.00

Calculate the

interplanar spacing,

and Bragg peak positions,

28,

for the 104 (the

strongest Bragg peak) and for the 0 12 (the lowest Bragg angle peak)

reflections assuming Cu Kal radiation with

1.5406

5. Consider

Figure

2.58,

which shows powder diffraction patterns collected

from the same material (CeRhGe3) at room temperature (T

295 K)

using x-rays and at T

200 K using neutrons. Setting aside differences

between intensities of individual Bragg peaks, the most obvious overall

difference between the two sets of diffraction data is that diffracted

intensity is only slightly suppressed towards high Bragg angles in

neutron diffraction, while it is considerably lower in the case of x-ray

data. Can you explain why?

Fundamentals of diffraction

259

6. Establish which combinations of indices are allowed and which are

forbidden in the space group symmetry

Cmc2,. List symmetry elements

that cause each group of reflections to become extinct?

7. Powder diffraction pattern of a compound with unknown crystal structure

was indexed with the following unit cell parameters (shown

approximately):

10.34 A,

6.02 A,

4.70 A,

90•‹,

90"

and

90". The list of all Bragg peaks observed from 15 to 60" 28 is

shown in

Table

2.19.

Analyze systematic absences (if any) present in this

powder diffraction pattern and suggest possible space groups symmetry

for the material.

Table

2.19.

List of Bragg peaks with their intensities and indices observed

a powder

diffraction pattern of a material indexed in the following unit cell:

10.34

6.02

4.70

and

90•‹,

90"

and

90".

hkl

1/10 20"

hkl

1/10 20"

2 0 0 255

17.105

202 207 42.154

101 583

20.712 321

59 44.296

10 207

22.629

212 47 44.899

011 77

23.966

4 2 0 19 46.246

11 1 741

25.495

501 17 47.978

201

120

25.572 0 2 2

133 49.120

211

665 29.598

031 15 49.339

020

106

29.650

122 28 49.961

301 327

32.152

131 123 50.166

2 2 0

34.448

511 68 50.470

311 1000

35.518

2 2 2 332 52.407

121 317

36.451

4 0 2 332 52.407

4 10 204

37.813

231 132 52.595

102 116

39.242

4 12 160 54.879

221

139

39.550

610 195 55.369

401 169

39.723

331 241 56.506

112 207

42.154

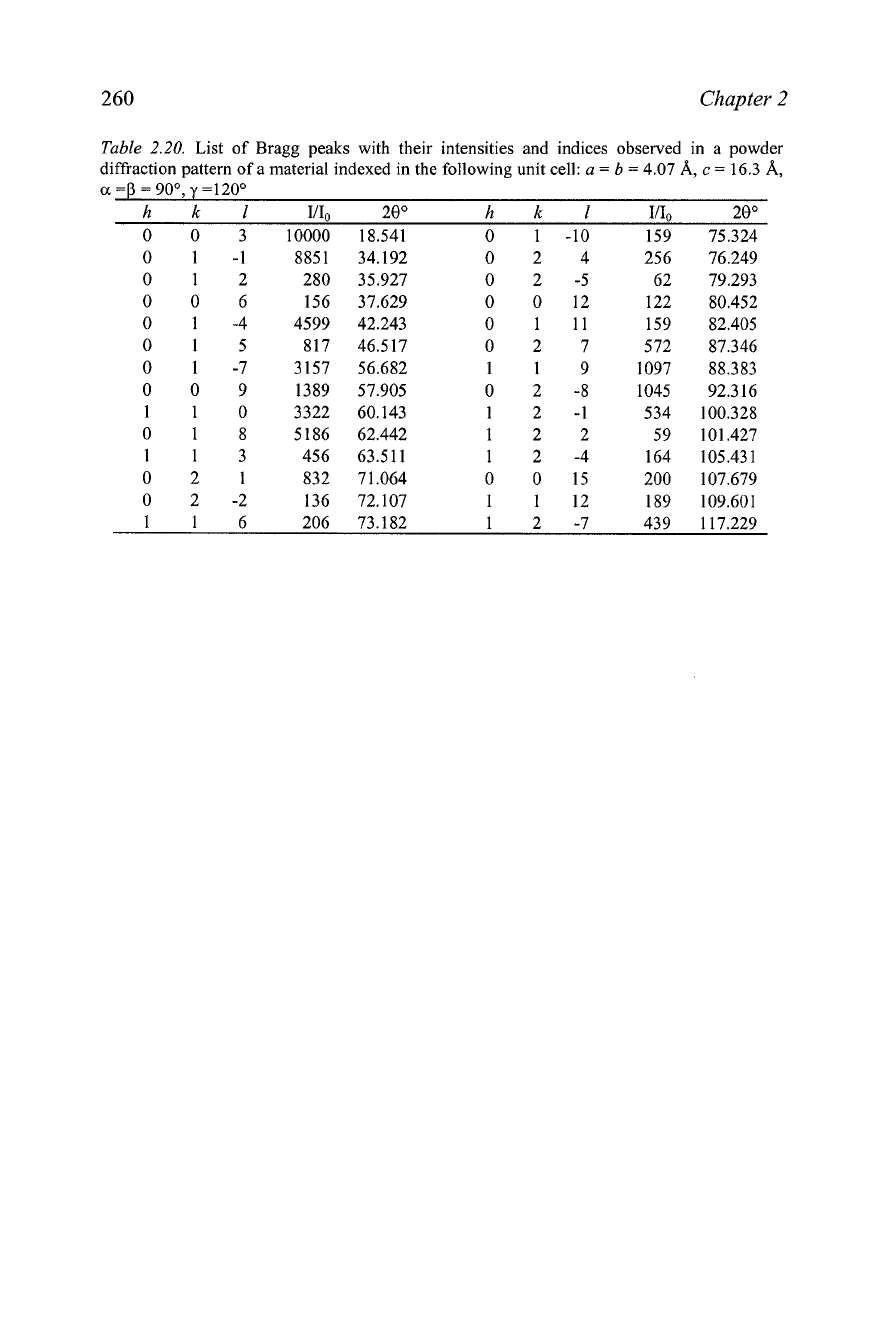
430 143 58.128

Powder diffraction pattern of a compound with an unknown crystal

structure was indexed with the following unit cell parameters:

4.07

16.3 A,

90•‹,

=120•‹. The list of all Bragg peaks

observed from 2 to 120" 28 is shown in

Table

2.20.

Analyze systematic

absences (if any) present in this powder diffraction pattern and suggest

possible space groups symmetry for the material

260

Chapter

Table

2.20.

List of Bragg peaks with their intensities and indices observed in a powder

diffraction pattern of

material indexed in the following unit cell:

4.07

16.3

90•‹,

=120•‹

hkl

I/Io

20'

hkl

I/Io

20"

0 0 3 10000

18.541 0 1 -10 159 75.324

0 1 -1

8851

34.192 024

256 76.249

012 280

35.927 0 2 -5 62 79.293

006 156

37.629

0 0 12 122 80.452

0 1 -4 4599 42.243 0

11 159 82.405

015 817 46.517 0 2 7 572 87.346

0 1 -7 3157

56.682 1 1 9

1097

88.383

0 0 9 1389

57.905 0 2 -8

1045

92.316

1 1 0 3322

60.143

1 2 -1 534

100.328

0 1 8 5186

62.442

122 59

101.427

113 456 63.511 1 2 -4 164 105.431

021 832 71.064 0 0 15 200 107.679

0 2 -2 136

72.107

1 1

12 189 109.601

116

206 73.182

1 2 -7 439 117.229