Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials
Подождите немного. Документ загружается.


Preliminary data processing and phase analysis
35
1
The following functions are commonly used in background (bi)
interpolation,' where
i
varies from
1
to
n
and
n
is the total number of data
points measured in a whole powder diffraction pattern or in the region
included in the processing:
-
Polynomial function, which approximates the background as
Here and below, B,, are background parameters that can be refined and
N
is the order of the polynomial. The summation in
Eq.
4.1 is usually
carried out beginning from m
=
0.
However, to account for the often
increased background at low angles, an additional (hyperbolic) factor
with m
=
-1 may also be included.
-
Chebyshev polynomial (type
I
or type 11, either shifted or not). It is
represented as a function of an argument xi, which is defined as
where
29n,i,
and
29,,,
are the minimum and maximum Bragg angles in
the powder diffraction pattern. The background is calculated as:
and the Chebyshev function, tm, is defined such that
where to
=
1 and
tl
=
x. Values of the function
t
are calculated using
tabulated coefficients.
-
Fourier polynomial, in which the background is represented as the
following sum of cosines:
Many other functions can be used to approximate the background. All of them should be
continuous functions of Bragg angle in the processed range.

352
Chapter
4
-
Diffuse background function to account for a peculiar scattering from
amorphous phases (e.g. see
Figure
4.2,
specimen
C)
or from a non-
crystalline sample holder:
where
Qi
=2ddi and the "d-spacing" is calculated for each point, 2Qi, of
the powder diffraction pattern.
In
Eqs.
4.1
to 4.6,
N
typically varies from 6 to 12 when the entire powder
diffraction pattern is of concern.
In
some instances, when profile fitting is
applied to short fragments of the powder diffraction pattern, the most
suitable background function is that given by Eq. 4.1 with
N
=
1 or 2, i.e. a
linear or parabolic background.
4.3.2
Smoothing
Smoothing is
a
numerical conditioning procedure employed to suppress
statistical noise, which is present in any powder diffraction pattern as a result
of random intensity measurement errors
(Eq.
3.8
in Chapter
3).
It improves
the appearance of the powder diffraction pattern. For example, smoothing
can make quickly collected data (say in a
15
min experiment) look similar to
a pattern collected in a longer (e.g. in an overnight) experiment, and may
help with certain automatic procedures, such as background subtraction,
Ka2
stripping and unbiased peak search.
Numerical conditioning, however, does not improve data quality.
Moreover, it causes broadening of Bragg peaks and loss of resolution
(e.g.
see
Figure
3.38
and
Figure
3.39
in Chapter
3,
which illustrate broadening
caused by the varying receiving slit) and may result in the disappearance of
weak peaks when overdone. On the contrary, increasing experiment time
improves the pattern since it reduces statistical spreads.'
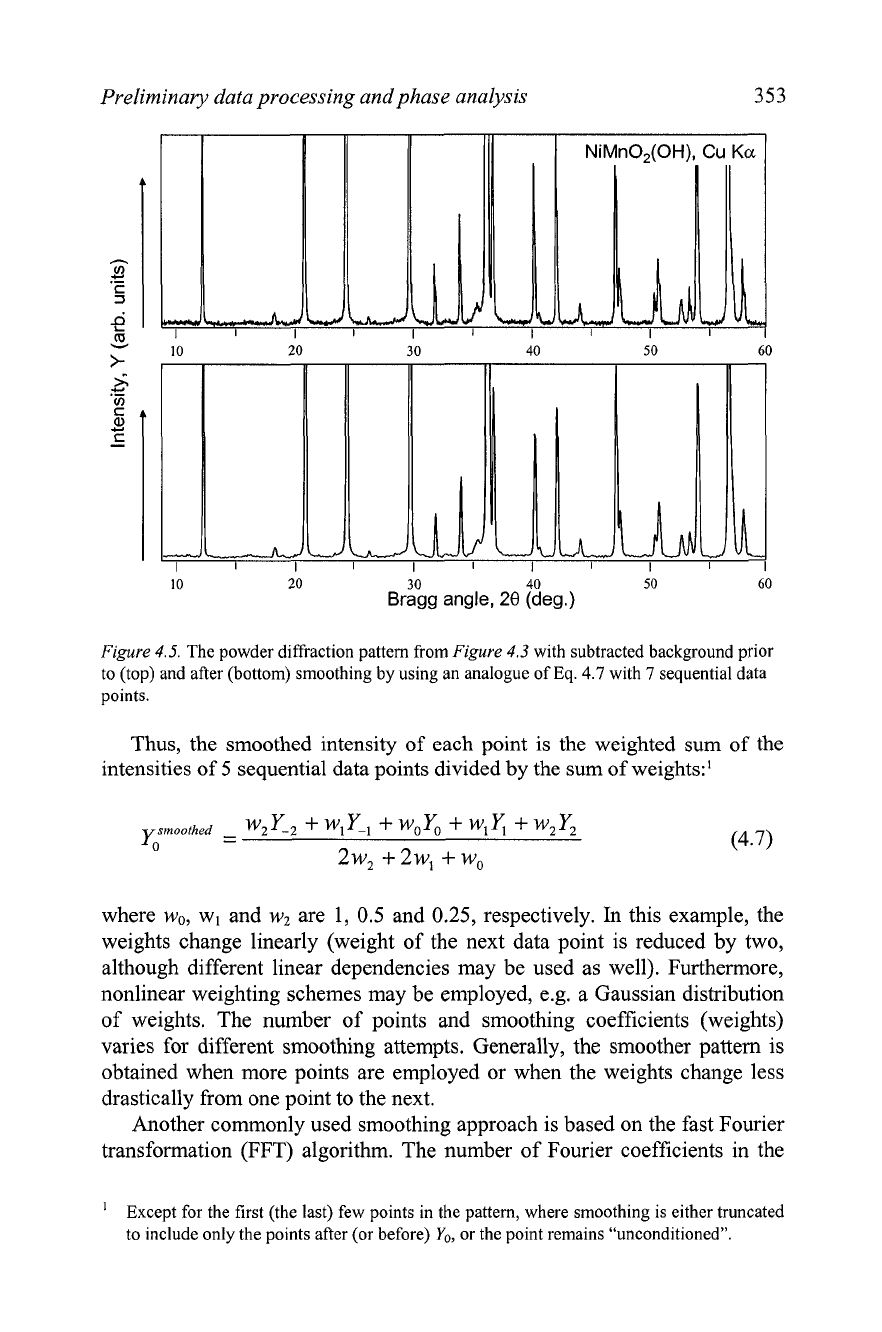
An
example of the
original and smoothed patterns is shown in
Figure
4.5.
The most typical smoothing approach is often called box car smoothing.
It involves averaging intensities of current and neighboring data points using
different weights. The weight is the largest for the point being smoothed and
it decreases rapidly for points located farther away. For example, when five
points are employed, the weights
(wi)
can be set at 1 for the point in the
middle (Yo),
0.5
for the nearest neighbors (Y+l), and 0.25 for the next nearest
neighbors
(Yk2).
As described in Chapter
3,
section
3.7.1,
a two-fold reduction of relative statistical errors
requires a four-fold increase of data collection time.
Preliminary data processing and phase analysis
353
30
40
Bragg angle,
29
(deg.)
Figure
4.5.
The powder diffraction pattem from
Figure
4.3
with subtracted background prior
to (top) and after (bottom) smoothing by using an analogue of
Eq.
4.7
with
7
sequential data
points.
Thus, the smoothed intensity of each point is the weighted sum of the
intensities of 5 sequential data points divided by the sum of weights:'
smoothed
-
~2
Y-2
+
~1'-1
+
WO~
+
~1
+
~2
'2
yo
-
2w2
+
2w1
+
wo
where wo, w1 and w2 are
1,
0.5 and 0.25, respectively.
In
this example, the
weights change linearly (weight of the next data point is reduced by two,
although different linear dependencies may be used as well). Furthermore,
nonlinear weighting schemes may be employed, e.g. a Gaussian distribution
of weights. The number of points and smoothing coefficients (weights)
varies for different smoothing attempts. Generally, the smoother pattern is
obtained when more points are employed or when the weights change less
drastically from one point to the next.
Another commonly used smoothing approach is based on the fast Fourier
transformation (FFT) algorithm. The number of Fourier coefficients in the
'
Except for the first (the last) few points in the pattem, where smoothing is either truncated
to include only the points after (or before)
Yo,
or the point remains "unconditioned".

354
Chapter 4
original pattern is equal to the total number of the observed data points. In
this case, the reverse Fourier transformation results in the original pattern.
Each Fourier coefficient corresponds to a signal of specific frequency
observed in the original pattern: the higher order coefficients represent the
higher frequency signals. Thus, when high order coefficients are set to zero
or lowered, the reverse FFT produces a pattern similar to the original but
with removed or reduced high frequency noise, or in other words, a
smoother pattern. Setting more high order coefficients at zero produces
stronger smoothing. As a result, the removal of high frequency noise
"improves" the pattern but at the same time, more and more fine details
(weak or narrowly split peaks) are lost. The loss of weak features in a pattern
is a common problem in any smoothing algorithm.
Similar to background removal, smoothing should never be applied to a
powder diffraction pattern, which will be later used for profile fitting or
Rietveld refinement.' When performed, smoothing may improve certain
figures of merit
(e.g. R,,, R, and X2, see Eqs. 6.18, 6.19 and 6.22 in Chapter
6, below), but it will likely and considerably distort lattice parameters and
most certainly all intensity-sensitive structural parameters, including
coordinates, displacement and population parameters of the individual
atoms. The only reliable and justifiable way to improve the true quality of
the full profile fit is to perform a more accurate (i.e. careful sample
preparation and/or longer counting time) powder diffraction experiment.
4.3.3
Ka2
stripping
The presence of dual wavelengths in conventional x-ray sources, or in
other words the presence of the Ka2 component in both the incident and
diffracted beams, complicates powder diffraction patterns by adding a
second set of reflections from every reciprocal lattice point. They are located
at slightly different Bragg angles when compared with those of the
main
(Kal) component. This decreases resolution and increases overlapping of
Bragg peaks, both of which have adverse effect on an unbiased peak search.
Since every
KallKa2 double peak is caused by scattering from a single
reciprocal lattice point, the d-spacing remains constant and the scattered
intensity is proportional to the intensities of the two components in the
characteristic spectrum. Using Braggs' law the following equation reflects
the relationship between the positions of the
diffraction
peaks in the doublet:
'
Unlike background removal, where the subtraction of a constant background is permissible
(see the footnote on page
348),
this statement has no exceptions.
Preliminary data processing and phase analysis
355
Furthermore, the integrated intensities of the two peaks are related as:
I,,
:Ifi2
=2:1
Assuming that peaks in the doublet have identical shapes, which is
reasonable because the separation between the two is usually small, although
it increases with increasing Bragg angle, Eqs.
4.8
and
4.9
may be applied to
every point of the observed peak shape, but not to the background. The Ka2
stripping usually starts from the lowest Bragg angle point of the first
observed peak, which should not be in the range of any other diffraction
maximum, and moves towards the last point in the pattern.
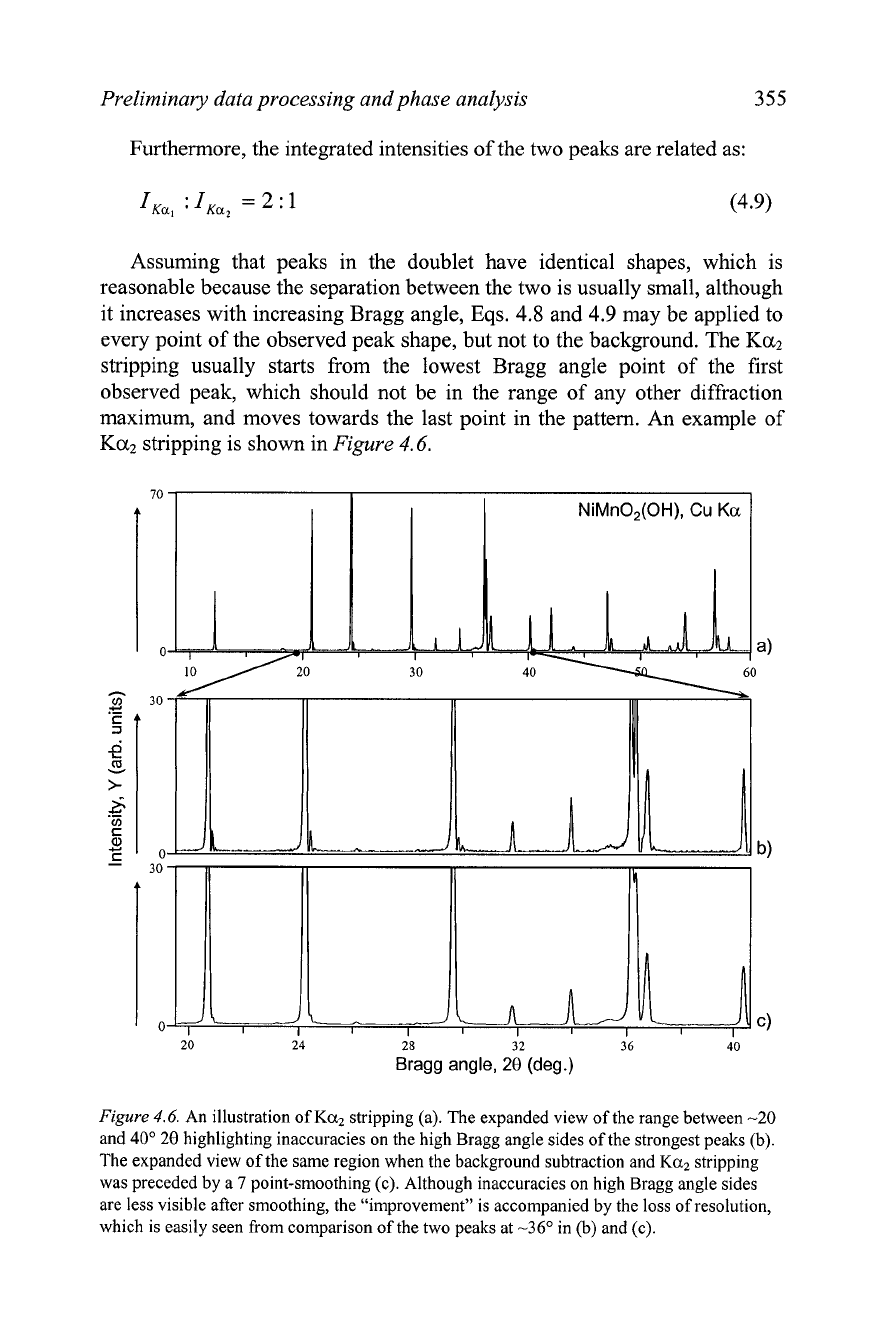
An
example of
Ka2 stripping is shown in
Figure
4.6.
20
24
28
32
36
40
Bragg angle,
20
(deg.)
Figure
4.6.
An illustration of
Ka2
stripping (a). The expanded view of the range between
-20
and
40"
20
highlighting inaccuracies on the high Bragg angle sides of the strongest peaks (b).
The expanded view of the same region when the background subtraction and
Ka2
stripping
was preceded by a
7
point-smoothing (c). Although inaccuracies on high Bragg angle sides
are less visible after smoothing, the "improvement" is accompanied by the loss of resolution,
which is easily seen from comparison of the two peaks at
-36'
in (b) and (c).

356
Chapter
4
It is easy to see that this simple approach is far from ideal and the
removal of the
Ka2
contributions is far from perfect. The inaccuracies occur
because it is difficult to eliminate the background precisely.
A
higher quality
pattern usually results in a better
Ka2
stripping as illustrated in
Figure
4.6~
where the same pattern was smoothed before removing the background and
Ka2
components. Visible peak broadening due to the smoothing treatment is
noteworthy.
One of the unfortunate results of
Ka2
elimination is the distortion of the
high angle slopes of all Bragg reflections. Therefore,
Ka2
stripping is a valid
step in the preparation of the powder pattern for the following automatic
peak search, but it
should never be
performed as a part of data conditioning
of the powder diffraction pattern for fitting andlor Rietveld refinement.
4.3.4
Peak
search
Fast and reliable peak search or peak localization is needed in order to
conduct either or both qualitative and quantitative phase analysis or database
search for matching
pattern(s). One of the most reliable (in terms of peak
recognition), but far from the fastest techniques, is locating peaks manually,
i.e. visually. This can be done in two ways: using the position of the peak
maximum or the mid-point of the peak's full width at half maximum. Both
cases require removing the
Ka2
contribution. If the latter is not done,
positions of both low angle peaks (where
Ka,
and
Ka2
contributions
essentially coincide) and high angle peaks (where these components are
nearly completely resolved) will be determined for the
Kal
components.
However, locations of peaks in the mid-angle range will be determined
somewhere between those of the
Kal
and
Ka2
components. Ideally, they
should correspond to the weighted average
Ka
wavelength (see
Table
2.1
in
Chapter
2)
but in reality this is difficult to achieve, especially when peak
tops are used as their positions. When
Ka2
components are stripped before
locating peaks, this problem is avoided and the positions of all peaks
correspond to the
Kal
part of the characteristic spectrum.
An
automatic peak search is actually the simplest (one-dimensional) case
in the more general two- or three-dimensional image recognition problem.
Image recognition is easily done by a human eye and a brain but is hard to
formalize when random errors are present and, therefore, difficult to
automate. Many different approaches and methods have been developed;
two of them are most often used in peak recognition and will be discussed
here. These are: the second derivative method and the profile scaling
technique.
The
second derivative method
is actually a combination of background
subtraction,
Ka2
stripping and, if needed, smoothing, which are followed by

Preliminary data processing and phase analysis
357
the calculation of the derivatives. This method is extremely sensitive to
noise. As a result, when fast measured patterns with substantial random
errors are employed, smoothing becomes practically mandatory. The second
derivative method consists of calculating first and then second derivatives of
Y(28) with respect to 28, and utilizing them in the determination of peak
positions. The derivatives can be easily computed numerically as:
ay.
-
q
-
a2q
qt2
-
2y.t1
+
y.
-
and
- -
820,
s
(320,)~
s2
where Yi,
Yiil
and
Yit2
are the intensities of three consecutive data points and
s
is the data collection step. Instead of smoothing, it is possible to use a
polynomial fit in the vicinity of every data point with the point in question
located in the middle of a sequence. Once the coefficients of the polynomial
are determined, both the first and second order derivatives are easily
calculated analytically. For example, for a third order polynomial (a
minimum of five sequential data points should be employed)
the first and second derivatives, respectively, are
and
where
x
is the Bragg angle. When the argument of the polynomial is selected
such that a point
&
(for which the derivatives are calculated) is chosen in the
origin of coordinates along the 28 axis, i.e. when
x
=
28
-
2ei, then the
corresponding derivatives are simply
c
(Eq. 4.12) and 2b (Eq. 4.13).
Some peak search algorithms use the first derivative, which is reliable
only for simple, well resolved patterns. The second derivative method works
better with complex data.
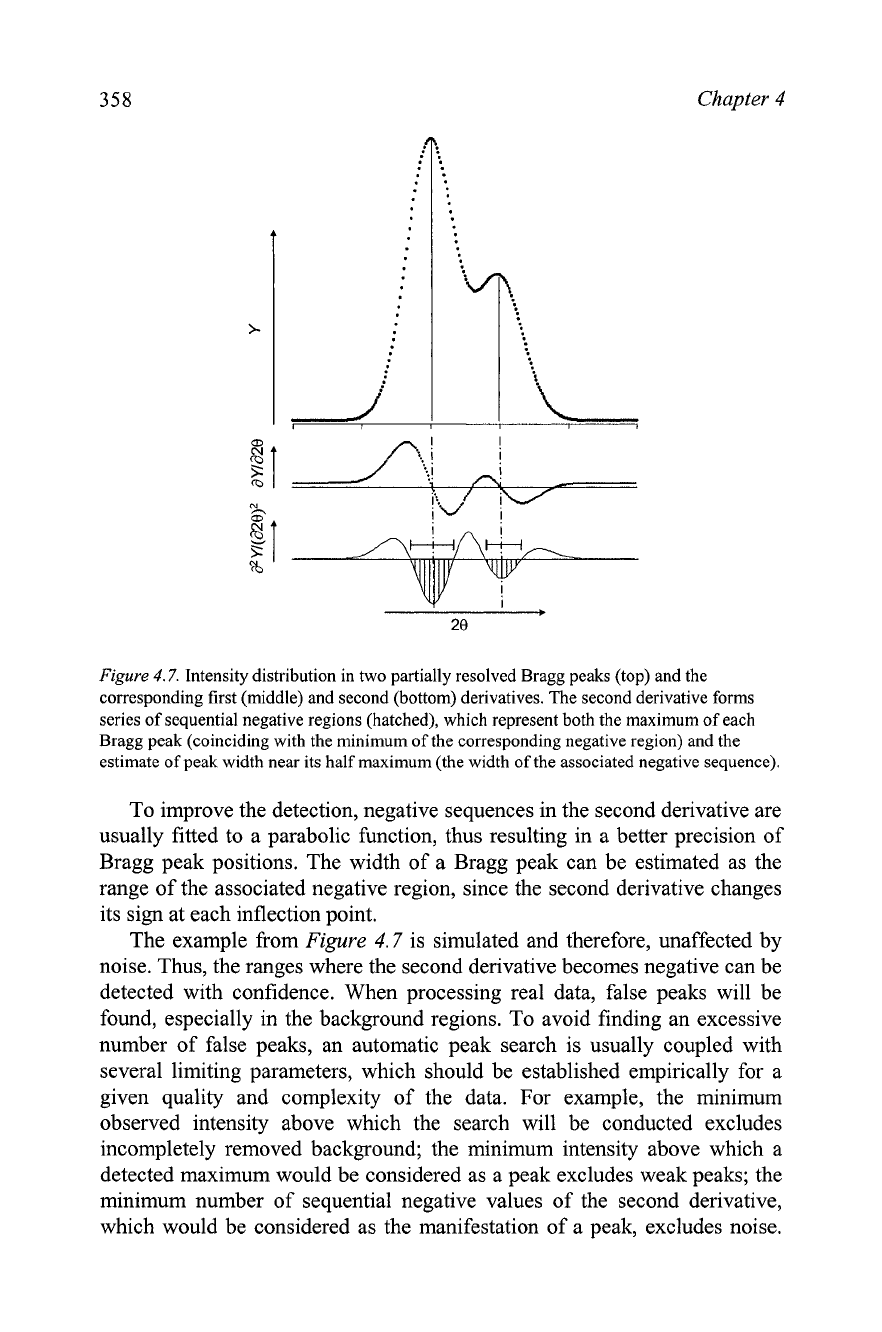
An
example in
Figure
4.7,
top shows the profile
representing two partially resolved Bragg peaks together with the first
(middle) and second (bottom) derivatives. The first derivative is zero at the
peak maximum and it changes sign from positive to negative when the
Bragg angle increases. The second derivative reveals each peak in a much
more reliable fashion, i.e. as a sequence of negative values of the function,
which are hatched in
Figure
4.7
for clarity.
Chapter
4
Figure
4.7.
Intensity distribution in two partially resolved Bragg peaks (top) and the
corresponding first (middle) and second (bottom) derivatives. The second derivative forms
series of sequential negative regions (hatched), which represent both the maximum of each
Bragg peak (coinciding with the minimum of the corresponding negative region) and the
estimate of peak width near its half maximum (the width of the associated negative sequence).
To improve the detection, negative sequences in the second derivative are
usually fitted to a parabolic function, thus resulting in a better precision of
Bragg peak positions. The width of a Bragg peak can be estimated as the
range of the associated negative region, since the second derivative changes
its sign at each inflection point.
The example from
Figure
4.7
is simulated and therefore, unaffected by
noise. Thus, the ranges where the second derivative becomes negative can be
detected with confidence. When processing real data, false peaks will be
found, especially in the background regions. To avoid finding an excessive
number of false peaks, an automatic peak search is usually coupled with
several limiting parameters, which should be established empirically for a
given quality and complexity of the data. For example, the minimum
observed intensity above which the search will be conducted excludes
incompletely removed background; the minimum intensity above which a
detected maximum would be considered as a peak excludes weak peaks; the
minimum number of sequential negative values of the second derivative,
which would be considered as the manifestation of a peak, excludes noise.
Preliminary data processing and phase analysis
359
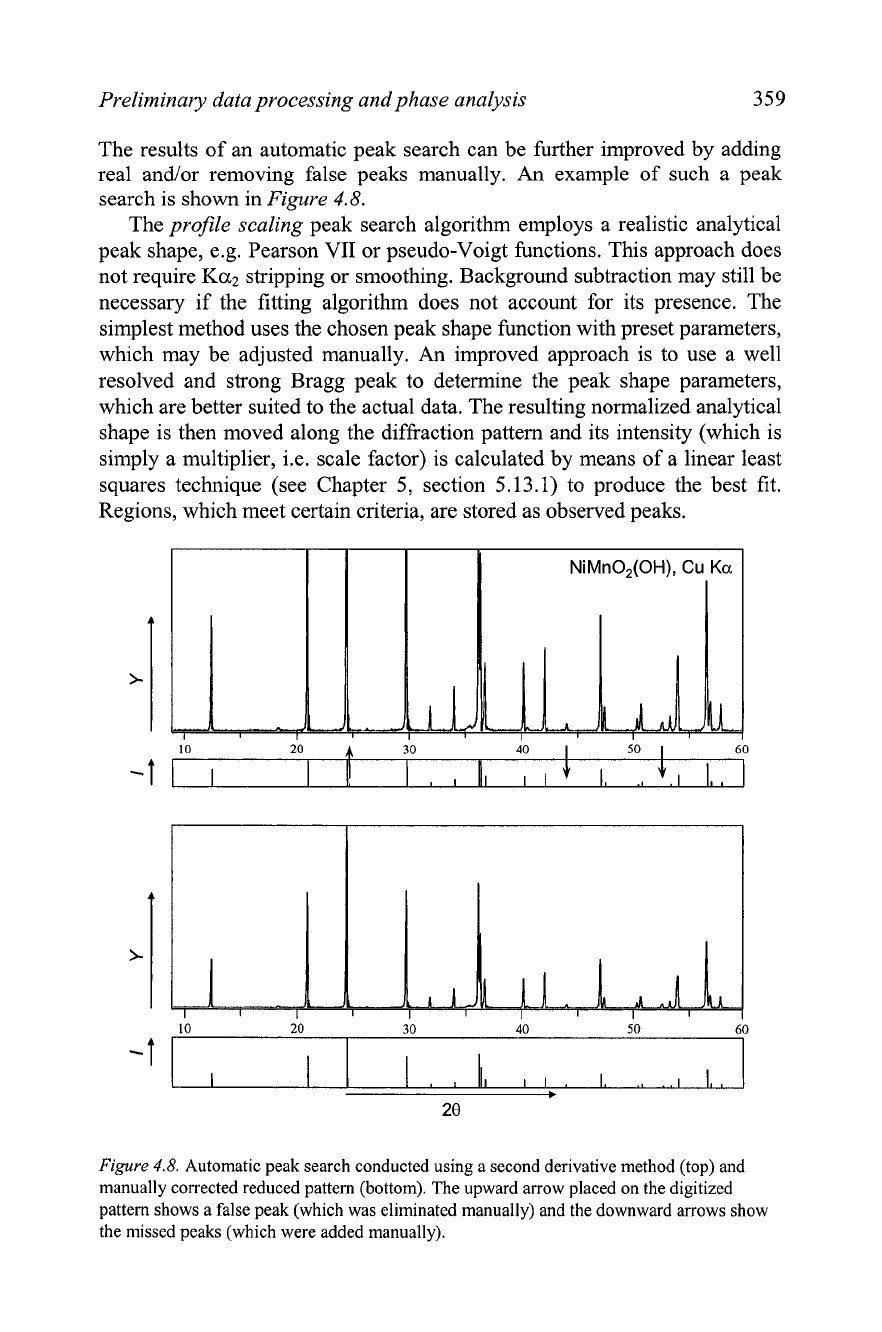
The results of an automatic peak search can be further improved by adding
real andlor removing false peaks manually.
An
example of such a peak
search is shown in
Figure
4.8.
The
profile scaling
peak search algorithm employs a realistic analytical
peak shape, e.g. Pearson
VII
or pseudo-Voigt functions. This approach does
not require
Ka2
stripping or smoothing. Background subtraction may still be
necessary if the fitting algorithm does not account for its presence. The
simplest method uses the chosen peak shape function with preset parameters,
which may be adjusted manually.
An
improved approach is to use a well
resolved and strong Bragg peak to determine the peak shape parameters,
which are better suited to the actual data. The resulting normalized analytical
shape is then moved along the diffraction pattern and its intensity (which is
simply a multiplier, i.e. scale factor) is calculated by means of a linear least
squares technique (see Chapter
5,
section
5.13.1)
to produce the best fit.
Regions, which meet certain criteria, are stored as observed peaks.
Figure
4.8.
Automatic peak search conducted using a second derivative method (top) and
manually corrected reduced pattern (bottom). The upward arrow placed on the digitized
pattern shows a false peak (which was eliminated manually) and the downward arrows show
the missed peaks (which were added manually).

3 60
Chapter 4
If necessary, an automatic peak search may be repeated using the
difference between the observed data and the sum of profiles of all detected
peaks. As a result, weak
andlor poorly resolved Bragg reflections, missed in
the previous search, may be found. This simple profile scaling method yields
relatively accurate peak positions and integrated intensities and, if
anticipated by the algorithm and realized in a computer code, their
FWHM's.
Its use is growing proportionally to the increasing computer speed. Since the
search remains automatic it may still require the adjustment of several
empirical parameters to exclude the excessive appearance of false peaks or
to improve the detection of weak Bragg reflections.
4.3.5
Profile
fitting
Profile fitting is the most accurate, although the slowest and the most
painstaking procedure resulting in observed peak positions, full widths at
half maximum, and integrated intensities of individual Bragg reflections. It
is based on minimization of the difference between observed and calculated
profiles using a non-linear least squares technique (see Chapter 6, section
6.6). The calculated profile is represented as a sum of scaled profiles of all
individual Bragg reflections detected in the whole pattern or in any part of
the pattern plus an appropriate background function (see section 4.3.1).
Individual peak profiles are described by one of the common peak shape
functions, typically pseudo-Voigt or Pearson-VII (see Chapter 2, section
2.9).
For conventional neutron diffraction data, a pure Gaussian function
may be employed.' Generally, three types of parameters can be adjusted
during the least squares fit:
-
Peak positions (28), are normally refined for the Kal components. If
present, the locations of the Ka2 constituents are established by Eq. 4.8.
-
Peak shape parameters, which include full width at half maximum
(H),
asymmetry (a), and exponent (P) for Pearson-VII or mixing parameter
(q) for pseudo-Voigt functions. All peak shape parameters are typically
refined for Kal reflections. The corresponding Kaz components are
assumed to have
H,
a,
p
(or q) identical to Kal. In some applications,
peak shape parameters may be fixed at certain commonly observed
values, or they may only be adjusted manually.
-
Integrated intensity
(I),
which is simultaneously a scaling factor for each
individual peak shape, see Eq. 2.48 in Chapter 2. Typically the integrated
intensity of the Kal reflection is a free parameter and the intensity of the
Ka2 part (if present) is restricted as given in Eq. 4.9.
'
It is worth noting, that when software on hand does not employ a Gauss peak shape
function, it can be easily modeled by the pseudo-Voigt function using the fixed mixing
parameter,
q
=
1.
