Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Thermodynamics of Discrete Systems 3

of the day and the night were respectively divided into seven and four parts, the

Babylonians 2,000 years beforehand divided the day and the night each into 12

hours, which were clearly of unequal duration and varied according to the seasons.

The Chinese and the Japanese divided each of the two cycles, from dawn to dusk

and from dusk to dawn, into six periods. Japan only adopted the occidental system in

1873, but this did not prevent Japanese clockmakers from making mechanical clocks

as early as the 17

century, these having quite complex mechanisms in order to

accommodate the variable length of their hour.

The definition and measurement of time are thus not automatic operations for

human beings. The relatively old notion of regular time (homogenous in the physical

sense) is related to the use of indefinitely reproducible phenomena; this notion dates

from the end of antiquity, the early Middle Ages and the invention of the clock

(clepsydras, mechanical clocks, hourglass).

We will thus postulate (Axiom 4) that physical phenomena are reproducible,

regardless of when an experiment is performed. Any evolutionary phenomenon

which is considered reproducible will allow a time unit to be defined. A temporal

dimension can be constructed simply by virtue of the reproducibility of a

phenomenon, which amounts to admitting that time is homogenous, i.e. no instant in

the universe is given any special privilege. This homogenity of time does not really

exist in cosmological problems, and in particular during the time of the initial big

bang. We exclude these kinds of problem.

Having long been attached to the average duration of a solar day, the definition

of time is now effected using the vibration frequency of an atom of caesium 123

under the most stable conditions possible (at very low temperature).

1.1.1.3. Causality and irreversibility

We now dispose of a space-time coordinates system comprising three space

dimensions and one time dimension. However, in contrast with geometric space,

time is not isotropic. In effect, the definition of entropy (section 1.2.2.4) shows that

an irreversible evolution exists in the universe with which we can associate a time

variable (or one related to the age of the universe) in an attempt to characterize it.

This irreversibility is explained by statistical mechanics whereby matter always

tends to states in which it is maximally mixed: gas molecules in a volume will

always be evenly dispersed over the volume. This is the most probable state in

which the molecules will be found; while the probability of finding all of the

molecules confined to the left half of the volume is not strictly zero, this situation is

never observed.

The age of the universe is thus associated with a measure of its entropy on a very

large scale (the universe or at least the earth). However, a time characterized by this

4 Fundamentals of Fluid Mechanics and Transport Phenomena

scale has no guarantee of being homogenous. This “age” of the universe does not

give us a useful indication of what time to use, and we will content ourselves with

the time previously defined from the notion of reproducibility. The notion of entropy

(or of the ageing of the universe) shows that time has a considerable anisotropy,

manifest in the distinction between the past, the present and the future. The

equations translating the physical laws and their consequences should not violate

this anisotropy, the effect of which can be immediately seen if we change the

direction of time by letting

tt  '.

Let us consider an isolated mechanical oscillator with friction, which can be

described by the equation:

0)()()(  tkxtxftxm



[1.1]

whose oscillatory solution takes the form



 tmtfA cos2/exp .

By multiplying equation [1.1] by )(tx



and integrating with respect to time

between 0 and T, the total variation of mechanical energy

between these

instants is:



 '

dtxfkxxmE



The absolute value of this variation 'E

is always negative and increasing for a

positive value of the friction coefficient. The quantity

dtxf



is known as the

dissipation function of the system.

Changing the direction of time would be equivalent to changing the term )(txf



to )(txf



 , which implies a negative friction coefficient f leading to the solution



 tmtfA cos2/'exp

and to an increase in mechanical energy as a time

function. This is impossible with an isolated oscillator and could only be made

possible by the intervention of an exterior energy source. The preceding equation is

clearly unstable in the sense that its solutions diverge analogously to the instabilities

encountered in the local study of equilibrium.

Let us take as an example three equations representative of constant coefficient,

second order partial differential equations (see Chapter 5):

Thermodynamics of Discrete Systems 5

Laplace equation:

wave equation:

heat equation:





The general solution of Laplace’s equation (which is elliptic) at a point requires

that conditions be known at all points lying on a curve surrounding this point

(Dirichlet condition). All points at the frontier of the domain exert an influence on

the solution at a point (

x,t). The result is that no physical phenomenon can be

represented by Laplace's equation if time is chosen as a variable, since the solution

t would depend on smaller (earlier) and larger (later) values of the time variable.

The wave equation (which is hyperbolic) on the contrary is compatible with the

definition of time. Its general solution:



)()(, txtxtxf 

represents two waves which propagate along the x-axis with velocities +1 and –1.

The value at a point

x and instant t depends on what happens to each of the said

waves to the left and the right of

x, and before their arrival at time t. The wave

equation is thus compatible with the non-influence of the future on the present.

The heat equation (which is parabolic) is also compatible with the non-influence

of the future on the present, as we will see for heat conduction problems, since the

initial conditions (or values from the past) suffice for a determination of the solution

at any later time.

Another remark can be made here regarding the inversion of the direction of

time. By replacing

t with  t', we see that the wave equation remains unchanged,

while the heat equation becomes:



We will see similar behavior for the complete solution of the heat equation in a

wall (Chapter 8) in which the inversion of the direction of time results in a change of

a sum of temporally decaying exponential terms to a sum of temporally increasing

exponential terms. Changing the direction of time in the heat equation leads to a

physically inadmissible equation.

The preceding phenomena can be interpreted in a number of ways:

6 Fundamentals of Fluid Mechanics and Transport Phenomena

1) In terms of energy dissipation and of the creation of entropy

The wave equation represents a frictionless mechanical phenomenon, there is no

creation of entropy over time; we have a reversible phenomenon and so an inversion

of the direction of time is not incompatible with the laws of the universe. We should

note however that the wave equation is only valid for relatively short times, for

which the inevitable friction is not to have an influence. Acoustic waves are finally

damped by diverse frictional forces after they have covered a very large distance;

light waves are finally absorbed by matter in an irreversible process (the Joule

effect) etc. Energy transfer creates entropy and is therefore compatible with the

evolution of the universe.

2) In terms of information loss

The wave equation was earlier interpreted as a transmission of a signal by pure

propagation. There is no loss of information during the transmission. The

introduction of dissipation (creation of entropy) leads to the telegrapher's equation,

which is no longer invariant under a change in the direction of time, and thus

involves an attenuation of the signals during transmission, and then a subsequent

loss of information.

The heat equation translates a smoothing of temperature distributions, which

may initially be complex, to a more uniform field. The final state is often a constant

temperature which has no memory of its initial distribution. We note again that an

inversion of the time direction in heat diffusion problems does not allow for a

retrieval of the information which has been lost. The same goes for an oscillator

with friction, whose final state of rest precludes any knowledge of the initial

conditions.

The notions of past and future, with respect to an event, introduce a fundamental

asymmetry; the present does not depend on the future. This has certain

consequences, both in the application of certain mathematical transformations

(Fourier for example) on temporal signals, and in flow problems where the

distinction between upstream and downstream is of the same nature as that between

the past and the future.

1.1.1.4.

Causality and determinism

The question of cause and effect is a very old philosophical problem (Aristotle,

the scholastic philosophers of the middle-ages, Descartes, Leibniz, Spinoza, Hume,

Kant, Schopenhauer, Bernard, etc.). We will not go into the complex philosophical

distinctions related to causes (adequate, inadequate, efficient, final, formal, material,

primary, secondary etc.). An effect is the result of and is produced by an efficient

cause.

Thermodynamics of Discrete Systems 7

Kant upholds that the causality relation is “absolutely general and even

necessary”. The general principle of causality is even more clear in determinism,

which holds that all events can be rationally predicted, with a desired degree of

precision, provided that past events and all of the laws of nature are known with

sufficient precision. Such absolute and universal determinism is associated with a

conception of a universe dominated by laws of celestial mechanics (Laplace). In

other words, the same causes produce the same effects, and so our capacity to

predict depends only on our scientific knowledge. Of course, quantum mechanics

has brought this vision of things into question, but not on the scale of the phenomena

studied here.

However, the question of determinism is not as simple as it might seem, in

particular in situations where unstable phenomena intervene, or where chance plays

a central role (chaos). Examples of such situations are usual in mechanical devices

used for games of chance (dice, roulette, etc.) or in fluid mechanics whose equations

have unstable solutions going through unpredictable evolutions in which flows are

fluctuating in a chaotic way. This is the phenomenon of turbulence encountered in

most practical flows; for example, atmospheric flows are results of such instabilities

and then weather prediction is fundamentally impossible beyond a few days.

Nevertheless, a statistical treatment of these turbulent flows leads to a more global

kind of determinism ([LES 98]).

It is useful to note at this point that the conditions for prediction can be defined

mathematically via theorems which treat of the existence of unique solutions for

differential equations given a suitable set of initial conditions. The Cauchy-Lipschitz

theorem is the best known, and deals with differential equations with real variables

(

x,y) of the form:

),( yxfdxdy

The function

f(x,y) is only required to verify a Lipschitz condition

. This theorem

establishes the existence of a unique solution

y =

M

(x) which verifies the initial

condition

M

) . This solution is continuous over the interval ),(

hxx  ,

where

h is characterized by the interval of definition for x and an upper bound of

in the rectangle considered. This theorem can be extended to systems of differential

equations with the same kinds of conditions.

A similar theorem (Cauchy-Kovalevskaïa), but with stricter analycity conditions

of the function

f(x,y) in the neighborhood of the point ),(

yx (functions which can

I.e.

')',(),( yyAyxfyxf 

, condition in which (x,y) and (x,y') are arbitrarily

chosen in a rectangle where f(x,y) is supposed to be continuous, A being a positive constant.

8 Fundamentals of Fluid Mechanics and Transport Phenomena

be developed in power series), leads to a unique analytic solution )(xy

in the

neighborhood of the point ),(

yx with the initial condition )(

. These

results can be extended to systems of differential equations, linear partial differential

equations, etc.

Cauchy’s theorem thus translates a form of determinism, since given a cause (the

initial condition )(

), a unique solution )(xy

exits. However, we see

that there are certain limitations, in particular with the Cauchy-Kovalevskaïa

theorem which imposes analyticity conditions, the physical realization of which has

no reason to be assured for the function f(x,y) or any other perturbation which we

may add in order to test the stability of the system

In all causal situations, the preceding Cauchy theorems lead to results of a local

nature, that is to say over a short period of time, considering the variable x to

represent time. In the middle to long term, numerous “mathematical accidents” may

occur. The uniqueness of a local solution is not in contradiction with the

impossibility of prediction of the evolution of this solution on a long enough period

of time due to a chaotic behavior ([BER 84], [ORS 77]).

In conclusion, the notions of determinism and causality are far from being

universally applicable in the domains which we will cover.

1.1.2. Systems analysis and thermodynamics

1.1.2.1. Introduction

The analysis of systems is a discipline which consists of constructing a model or

a representation of a system characterized by observations and measurements, with a

view to predicting the behavior of this system at a later stage, under conditions

which may be different from those first encountered. We also attempt to contrive

means of manipulating the system in order to cause it to evolve in a manner which

we specify a priori. We thus enter into the domain of command and control, since it

is now necessary to verify that the results are those sought, and if not, to perform the

necessary corrections in order to obtain the desired results.

The characterization of a material device can thus vary depending on the

objective which we seek to achieve. The device may be static and we may only be

interested in its “state”; it may be dynamic, in which case it evolves as a time

function.

In general, the objective of a system is to transform some input quantities u(t),

known thanks to some measurement (which provides the input variables), into some

Thermodynamics of Discrete Systems 9

output quantities y(t) which are also obtained via a measurement (output variables).

For example, the input variables of a heating system are the available heating power,

the desired temperature, and the output (controlled) variables are the power

consumed and the temperature observed in the space to be heated. We also dispose

of a command variable for the heating system. The input variables are thus the given

conditions, while the output variables are the quantities obtained. Observations can

be made for the time evolution of the various quantities in a continuous or sampled

manner.

1.1.2.2.

External description (black box)

The description of a system may be external, that is we satisfy ourselves to

simply measuring the inputs and outputs of the system, the system itself remaining a

“black box”. We thereby ignore what goes on inside the system. As the system

operates we measure y(t) which depends on the input u(t) and time t. Often, the

system “has a history”, and the output y(t) cannot be represented as a function of the

only two variables u(t) and t.

The external description of a state is thus generally not sufficient. The difference

between a raw egg and a hard-boiled egg is not visible to external measurements

(size, mass, color, etc.); it is a result of internal variables (chemical composition)

which cannot be measured directly, but which can be known indirectly (the

rotational movement of a mass of solid and a mass of liquid are not the same), or by

virtue of some previous known history (the egg was boiled).

From a mathematical point of view, the black box description corresponds to a

direct relationship between the inputs and the outputs, in other words to calculations

defined a priori on the input quantities. As long as the dynamic system is invariant

in time, the formalism of transfer functions (or of impulse responses) is largely used.

It is nonetheless necessary to pay close attention to questions of causality when

using such approaches (see Chapter 7; for more detailed information, the reader is

referred to works which deal with signal processing and automatic control theory).

1.1.2.3.

Internal description (state variable approach)

In place of a “black box” description, we substitute a description of the internal

state of the system using a number of state variables X(t) (state vector). These

characterize the “state” of the system, and when combined with a knowledge of the

system inputs, knowledge of the system outputs can be obtained at every instant by

means of evolution equations (ordinary or partial differential equations) which

describe the conditions on geometric boundary of the system and the initial state.

10 Fundamentals of Fluid Mechanics and Transport Phenomena

The simplest dynamic systems are represented by constant-coefficient linear

differential equations; these are known as invariant linear systems as their response

does not depend on the initial instant chosen for the study of their evolution:

000

)( :);( XtXtttBUAX



In order to identify a state representation, we can use purely mathematical

considerations which are essentially based on the nature of the response of the

system (system outputs) to a specific excitation (Dirac impulse or step function). If it

is possible to identify the existence of different time constants, for example W

and

, then the behavior of the system can be considered to be second order, which

implies the need for a description based on two state variables. State variables

identified via an empirical modeling approach will not necessarily lend themselves

to a clear physical interpretation. They are merely indicators which are linked in

some way to the dominant physical quantities of the system. We will come back to

this point when we discuss model reduction methods (Chapter 8).



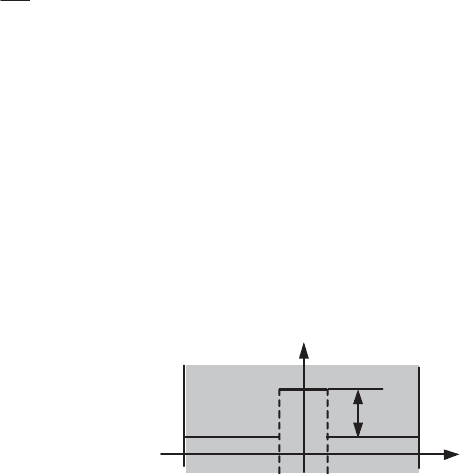
Figure 1.1. Temperature pulse function unrealizable from imposed conditions

on the walls (identical temperature on the two walls)

Finally, we may wish to manipulate certain system variables in order to achieve

a given desired state. From a mathematical point of view, boundary conditions must

of course exist which allow a solution of the local equations (partial differential

equations) corresponding to the evolution of the physical system towards such a

final state. This condition is not always satisfied, as shown in Figure 1.1. In this

example, the physical system considered is not controllable.

1.1.2.4.

Thermodynamics and mechanics

This chapter and Chapter 2 are dedicated to a presentation of those basic physical

laws which are valid regardless of the particular properties of the material elements

considered. These basic laws constitute thermodynamics and mechanics; they need

to be completed by means of other particular laws which may play a role in the

Thermodynamics of Discrete Systems 11

behavior of the material elements, associated for example with physics (state

equations of compressible fluids), chemistry, electricity, magnetism,

electromagnetism, or any combination of these disciplines (laser-matter interactions,

plasmas, chemical reactions or electrolysis in flows, etc.).

The laws of thermodynamics derive from the laws of mechanics applied to

ensembles comprising a very large number n of molecules (statistical mechanics).

The properties resulting from interactions between these n molecules cannot be

exactly established for a variety of reasons (residual quantum effects, computations

rendered impossible for very large numbers of particles, etc.). We therefore need to

complete our microscopic mechanical models (kinetic theory of gas, molecular

theory of liquids) by means of additional statistical axioms.

Thermostatics provides interpretations of physical quantities using the notion of

balance via the intermediary of extensive quantities. This is the equivalent of

imposing conservation principles for certain quantities, whose creation,

disappearance or variation is not spontaneous, but which is associated with a clear

cause that results in the transformation or displacement of the quantity considered.

This static study of the properties of material systems is firstly made in a reference

frame in which the material does not move, or at least under conditions such that the

effects of movement have no effect on this material.

When considering balances, a knowledge of time only serves to localize various

instants, while its definition is not important due to the infinitely slow nature of

thermostatic transformations. On the contrary, the definition of time in

thermodynamics is of great importance for the study and the prediction of the

velocity of a system’s temporal evolution. On the other hand, the equations of

thermodynamics and its related disciplines must be associated with boundary and

initial conditions which allow solutions that are actually observed in reality.

1.1.3. The notion of state

In thermodynamics, a state is a set of material elements which have well-defined

properties. In order to characterize the state (a) of this ensemble, physical quantities

must be defined which can be measured (measurements g

) and which allow us to

distinguish between these and other material elements, or the same elements at

another instant, after a transformation. From a mathematical point of view, a state is

thus constituted by an ensemble of variables g

which characterize the material

contained in some entity or geometric domain. States thus defined obey the usual

rules of the set theory ([GIL

64], [BOC 92]). We often refer to this material as being

in state (a). It is clear that once defined as being in a given single state, the notion of

a system does not supply any additional information with respect to the notion of

12 Fundamentals of Fluid Mechanics and Transport Phenomena

state. The state of a system may be more or less complex and its description may

require a more or less large number of variables, depending on the case considered.

As an example, let us consider 2n contiguously arranged plates of a homogenous

material (Figure 1.2a) distributed in three separate blocks by two thin thermally

insulated layers P

and P

. Suppose that the notion of temperature is known (for this

example); half of these plates are at a temperature T

which is greater than the

temperature of the other half (Figure 1.2a). The description of this initial state thus

requires that 2n temperatures be given. Let us now cause this state to evolve, under

the constraints imposed by the thermally insulated lateral faces. These 2n variables

are not necessarily required; the walls P

and P

play the role of a strong thermal

resistance, the blocks of plates have an approximately uniform temperature at each

instant (Figure 1.2b); these three temperatures suffice for a description of the state of

the system and its subsequent temporal evolution. After a sufficiently long time, the

state is at a uniform temperature

. This final state, which is described

by a single variable is clearly in a state of equilibrium.

(a) (b)

Figure 1.2. (a) System with 2n variables; (b) system with 3 variables

The general problem of describing a state comes down to finding the necessary

variables. From the preceding example we see that the number of necessary

variables depends largely on the physical situation we wish to describe. The more

complex the system considered, the greater the number of variables required. We

will frequently come back to this point, emphasizing it with respect to the specific

objectives.

A state of equilibrium is in fact a succession of states for which all of the

variables that constitute it conserve a constant value, physical exchanges with the

exterior having ceased.