Полшков Ю.Н. Курс лекций по экономико-математическому моделированию
Подождите немного. Документ загружается.


100
2) Нахождение корреляционной матрицы:
*/ *
1 0,5591 0,9789
1
0,5591 1 0,5137
0,9789 0,5137 1
rXX
n
−
⎛⎞
⎜⎟
== −
⎜⎟
⎜⎟
−−
⎝⎠
.
Её определитель: .
det( ) 0,0276r =
При имеется полная мультиколлинеарность, а если
det( ) 0r = det( ) 1r
=
,
то мультиколлинеарность отсутствует. В нашем случае
0det()r 1
<
< , поэтому
продолжим исследование на наличие мультиколлинеарности.
3) Определение фактического значения критерия “хи”-квадрат:
[]
2
1
1 (2 5) ln det( ) 25,7279
6
nm r
χ
⎡⎤
=− − − + =
⎢⎥
⎣⎦
.
Фактическое значение критерия
2
χ
сравнивается с табличным значением
при
1
(1)
2
mm+=6
степенях свободы и уровне значимости 0, 05
α
=
:
. Т.к.
2
12,5916
t
χ
=
2
t
2
χ
χ
> , то в массиве объясняющих переменных сущест-
вует мультиколлинеарность.
4)Определение обратной матрицы:
1
26,6709 2,0386 25,0604
2, 0386 1,5143 1, 2177
25,0604 1, 2177 24,9056
Cr
−
−
⎛⎞
⎜⎟
==− −
⎜⎟
⎜⎟
−
⎝⎠
.
5) Вычисление -критериев:
F
1
51,3419F
=
;
2
1, 0286F
=
;
3
47,8112F
=
.
Фактические значения критериев сравниваются с табличным при
3m
=
и
степенях свободы и уровне значимости
16nm−−=
0, 05
α
=
: .
Т.к. и , то независимые переменные
4, 7571
t
F =
1 t
FF>
3 t
FF>
1
x
и
3
x
мультиколлинеар-
ны с другими. Коэффициент детерминации для каждой переменной:
[
]
2
1
( ) 0,9625Rx = ;
[
]
2
2
( ) 0,3396Rx = ;
[
]
2
3
( ) 0,9599Rx = .
6) Нахождение частных коэффициентов корреляции:
12
0,3208r = ;
13
0,9724r
=
− ;
23
0,1983r
=
.
7) Вычисление
t-критериев:
12
0,8296t
=
;
13
10,1981r
=
− ;
23
0, 4955r
=
.
Фактические значения критериев сравниваются с табличным при
степенях свободы и уровне значимости
16nm−−=
0, 05
α
=
: .
Т.к.
2, 4469
T
t =
13 T
t> t, то между независимыми переменными
1
x
и
3
x
существует муль-
тиколлинеарность.
101
Для того, чтобы избавиться от мультиколлинеарности, можно исключить
одну из переменных мультиколлинеарной пары
1
x
и
3
x
. Удалить следует пере-
менную
1
x
, т.к. у неё больше значение -критерия. Следовательно, она больше
влияет на общую мультиколлинеарность модели. Однако этот шаг не должен
противоречить экономическому смыслу задачи.
F
Пример приведен полностью.
102
Лекция 8
ГЕТЕРОСКЕДАСТИЧНОСТЬ
План лекции
1. Понятие гетероскедастичности.
2. Проверка гетероскедастичности на основе критерия
μ
.
3. Проверка гетероскедастичности параметрическим тестом Гольд-
фельда-Квандта.
1. При изучении теоремы Гаусса-Маркова, предполагалось, что спецификация
линейной многофакторной эконометрической модели следующая:
11 2 2
...
iiimim
yabxbx bx
i
ε
=+ + ++ +,
где – номер наблюдения.
1,...,i= n
Одним из условий, на которые опиралась данная теорема, была гипотеза
3. А именно, математические ожидания случайных величин
i
ε
равны нулю:
() 0
i
M
ε
= . Дисперсии:
2
() ( )
ii
DM
2
ε
εσ
=
= . Причём значения математиче-
ских ожиданий и дисперсий ошибок не зависят от номера наблюдений .
i
Условие независимости дисперсии ошибок от номера наблюдения назы-
вается гомоскедастичностью. Нарушение данного условия вызывает нежела-
тельное явление, называемое гетероскедастичностью.
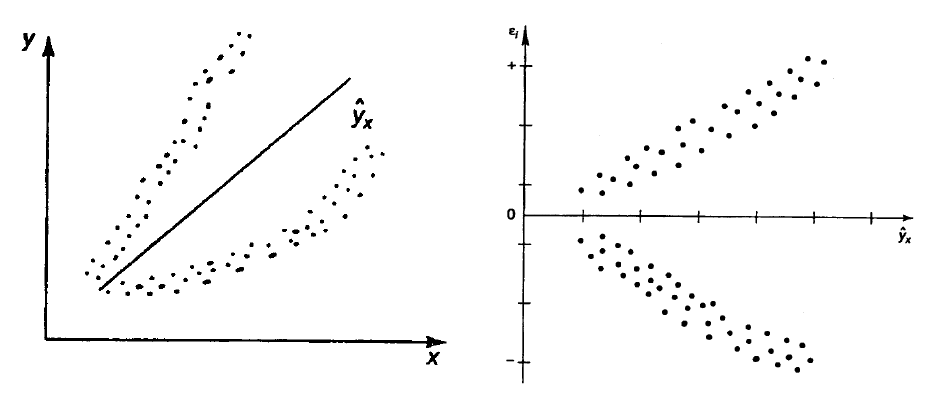
На рис.1 гетероскедастичность проиллюстрирована графически: а) дис-
персия остатков растет по мере увеличения
x
; б) – дисперсия остатков достига-
ет максимальной величины при средних значениях переменной
x
и уменьша-
ется при минимальных и максимальных значениях
x
; в) – максимальная дис-
персия остатков при малых значениях
x
и дисперсия остатков однородна по
мере увеличения значений
x
. Наличие гетероскедастичности можно видеть и
по графику зависимости остатков
i
ε
от теоретических значений результативно-
го признака
x
y .
а)
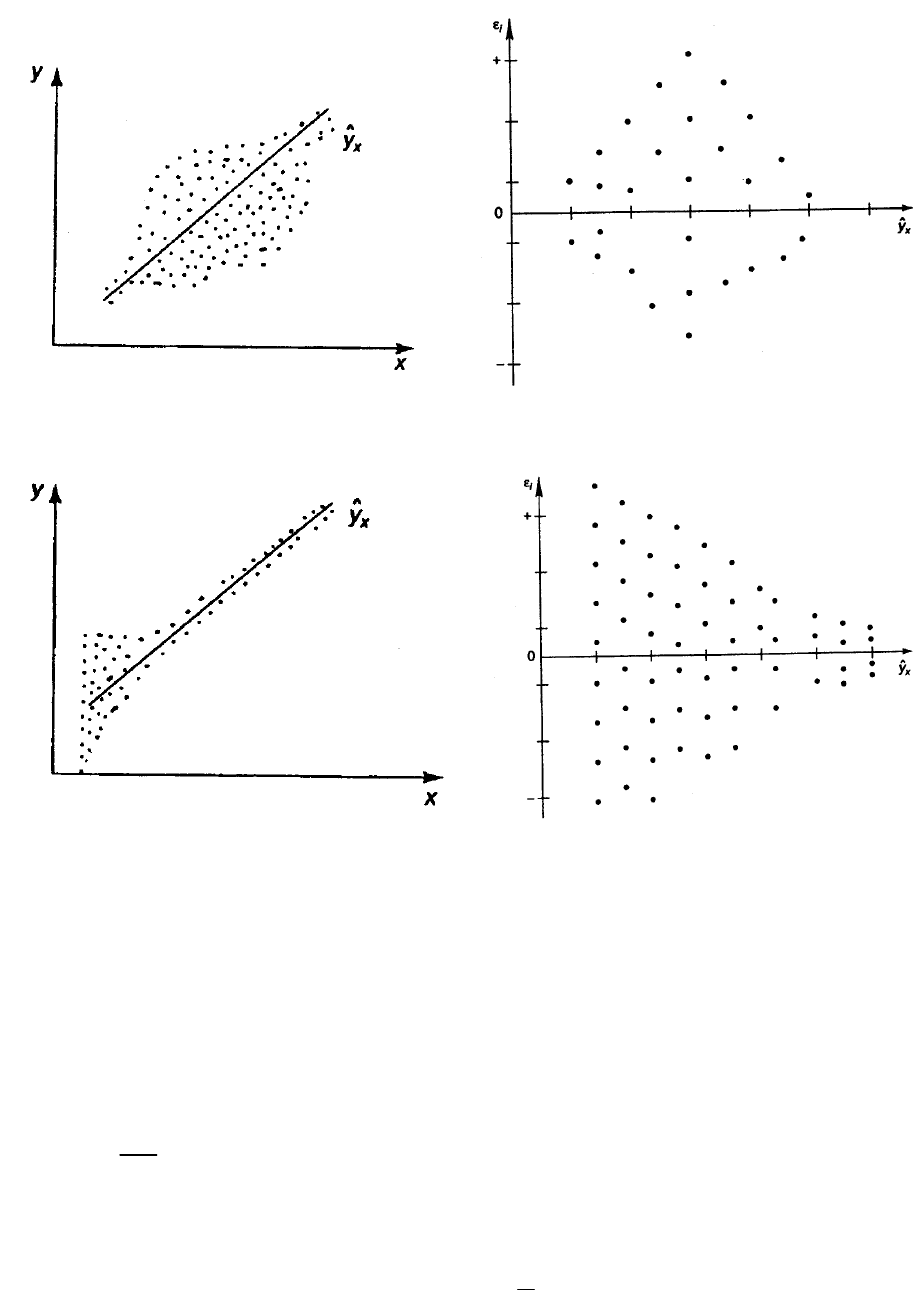
103
б)
в)
Рис. 1. Примеры гетероскедастичности
2. Рассмотрим критерий
μ
, позволяющий проверять наличие
гетероскедастичности.
Этот метод желательно применять тогда, когда исходная совокупность
наблюдений достаточно велика, то есть или около этого. Приведём со-
ответствующий алгоритм.
20n ≥
1) Исходные данные столбца зависимой переменной
Y разбиваются на
групп,
k
1,r= k
. Желательно, чтобы группы соответствовали разным уровням
величины . Т.е. их надо упорядочивать, например, в порядке возрастания.
y
2) По каждой группе данных вычисляется сумма квадратов отклонений:
()
2
1
r
n
rir
r
i
Syy
=
=−
∑
.
3) Определяется сумма квадратов отклонений в целом по всей совокупно-
сти наблюдений:

104
()
2
111
r
n
kk
rir
r
rir
Sy
===
=−
∑∑∑
y.
4) Вычисляется параметр :
w
2
2
1
1
r
n
k
n
r
k
rr
r
r
S
S
w
nn
=
=
⎛⎞
⎜⎟
⎛⎞
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
⎜⎟
⎝⎠
∑
∏
,
где – общее количество наблюдений; – количество наблюдений -ой гру-
ппы.
n
r
n r
5) Вычисляется критерий:
2lnw
μ
=
− ,
приближенно соответствующий распределению
2
χ
в том случае, когда диспер-
сия остатков для всех наблюдений однородна. Таким образом, если
2
t
μ
χ
> , то
при выбранном уровне значимости
α
и числе степеней свободы наблю-
дается гетероскедастичность.
1k −
3. Часто при исследовании совокупности данных на гетероскедастичность
предполагается, что дисперсия остатков пропорциональна квадрату значений
одной из независимых переменных
j
x
.
В этом случае наиболее эффективен параметрический тест Гольдфель-
да-Квандта. Опишем его алгоритм.
1) Упорядочить наблюдения в соответствии с величиной элементов век-
тора
j
X .
2) Отбросить наблюдений, содержащихся в середине вектора. Согласно
с экспериментальными расчетами авторы теста нашли оптимальные соотноше-
ния между параметрами
c и , где – количество элементов вектора
c
n n
j
X :
4
15
c
n
=
.
3) Построить две эконометрические модели на основе 1МНК по двум об-
разованным совокупностям наблюдений объёмом
1
2
nc
n
−
= и
2
2
nc
n
−
=
при
условии, что этот объём превышает общее количество независимых перемен-
ных
m
, входящих в модель.
4) Найти сумму квадратов остатков и для первой и второй моделей,
соответственно:
1
S
2
S
/
111
S
ε
ε
=
/
222
S;
ε
ε
= .

105
5) Вычислить критерий , разделив большую сумму квадратов остатков
на меньшую. Рассчитанное значение сравнивается с табличным значением
критерия Фишера для степеней свободы
*
R
*
R
t
F
1
(2kncm=−− )2,
2
(2)kncm=−− 2 и выбранного уровня значимости
α
. При гетеро-
скедастичность имеет место.
*
t
RF>
Пример 1. В табл. 1 приведены данные по зависимой переменной и
независимым переменным
y
12
,,
3
x
xx. Требуется проверить наличие гетероске-
дастичности с помощью: а) критерия
μ
; б) параметрического теста Гольдфель-
да-Квандта.
Табл. 1. Данные задачи
№
y
1
x
2
x
3
x
1 -2,66 0,68 0,42 25,68
2 1,41 0,74 0,05 18,13
3 -2,79 0,66 0,29 25,74
4 0,42 0,72 0,48 21,21
5 -2,24 0,68 0,41 22,97
6 1,41 0,77 0,62 16,38
7 1,89 0,78 0,56 13,21
8 0,36 0,78 1,76 14,48
9 1,18 0,81 1,31 13,38
10 5,18 0,79 0,45 13,69
11 1,44 0,77 0,5 16,66
12 1,55 0,78 0,77 15,06
13 0,09 0,72 1,2 17,6
14 1,9 0,79 0,21 15,98
15 1,43 0,77 0,25 18,27
16 5,39 0,8 0,15 14,42
17 -2,3 0,71 0,66 22,76
18 1,42 0,79 0,74 15,41
19 1 0,76 0,32 19,35
20 0,91 0,78 0,89 16,83
21 -3,76 0,62 0,23 30,53
22 1,12 0,75 0,32 17,98
23 0,03 0,71 0,54 22,09
24 0,55 0,74 0,75 18,29
25 -2,76 0,65 0,16 26,05
26 -2,78 0,66 0,24 26,2
27 1,72 0,84 0,59 17,26
28 0,61 0,74 0,56 18,83
29 0,5 0,75 0,63 19,7
30 0,61 0,75 1,1 16,87

106
Решение. а) Применим критерий
μ
.
1) Упорядочим исходные данные столбца зависимой переменной по
возрастанию. Разбиваем его на
Y
3k
=
группы. Объём наблюдений в каждой
группе равен 10.
Группа 1 Группа 2 Группа 3
-3,76 0,42 1,41
-2,79 0,5 1,42
-2,78 0,55 1,43
-2,76 0,61 1,44
-2,66 0,61 1,55
-2,3 0,91 1,72
-2,24 1 1,89
0,03 1,12 1,9
0,09 1,18 5,18
0,36 1,41 5,39
2) По каждой группе данных вычисляем сумму квадратов отклонений:
1
19, 40789S = ;
2
1, 03049S
=
;
3
22,12161S
=
.
3) Определяем сумму квадратов отклонений в целом по всей совокупно-
сти наблюдений:
3
1
42,55999
r
r
S
=
=
∑
.
4) Вычисляем параметр , с учётом того, что
w 30n
=
:
()()
(
)
()
55 5
15
19, 40789 /10 1, 03049 /10 22,12161/10
0, 00008933
42,55999 /10
w
⋅⋅
==
.
5) Вычисляем критерий:
2ln(0,00008933) 18,64638
μ
=− = .
При и
12k −= 0, 05
α
= табличное значение .
2
5,991476
t
χ
=
Т.к.
2
t
μ
χ
> , то в массиве данных наблюдается гетероскедастичность с
надёжностью не менее 95%.
б) Применим параметрический тест Гольдфельда-Квандта.
Предположим, что дисперсия остатков пропорциональна квадрату значе-
ний одной из независимых переменных
j
x
. Графически определим эту пере-
менную. Построим поля парной корреляции (рис. 2).
Как видно на рис. 2 б), источником гетероскедастичности является, ско-
рее всего, переменная
2
x
. График имеет сходство с ситуацией на рис. 1 в).
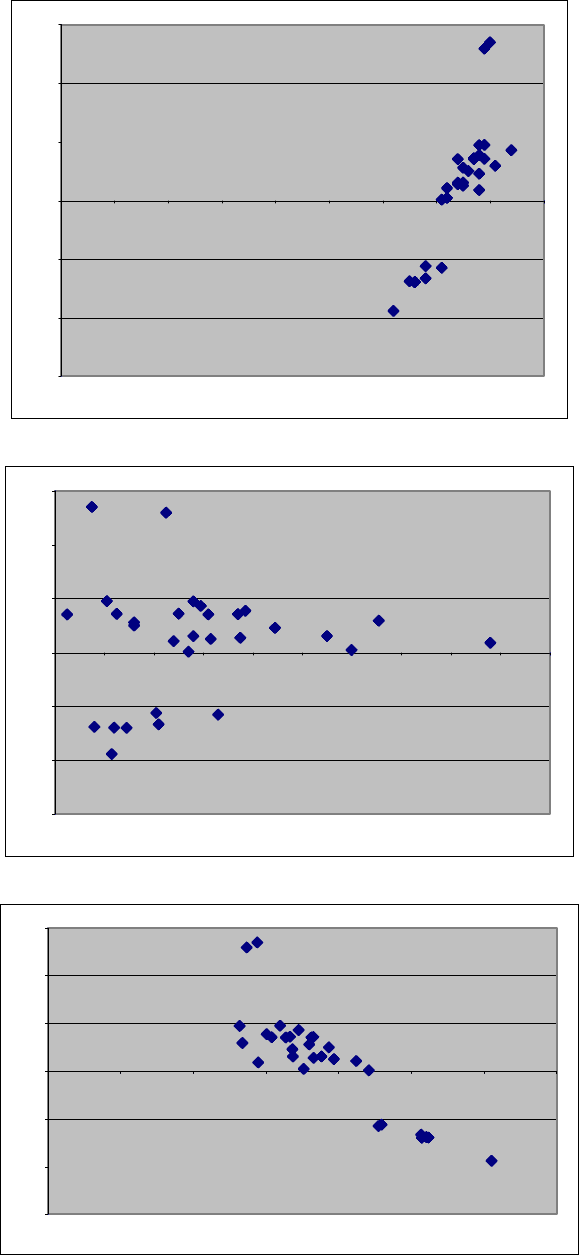
107
-6
-4
-2
0
2
4
6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
x1
y
а)
-6
-4
-2
0
2
4
6
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2
x2
y
б)
-6
-4
-2
0
2
4
6
0 5 10 15 20 25 30 35
x3
y
в)
Рис. 2. Поля парной корреляции между: а)
1
x
и ; б) y
2
x
и ; в) y
3
x
и . y
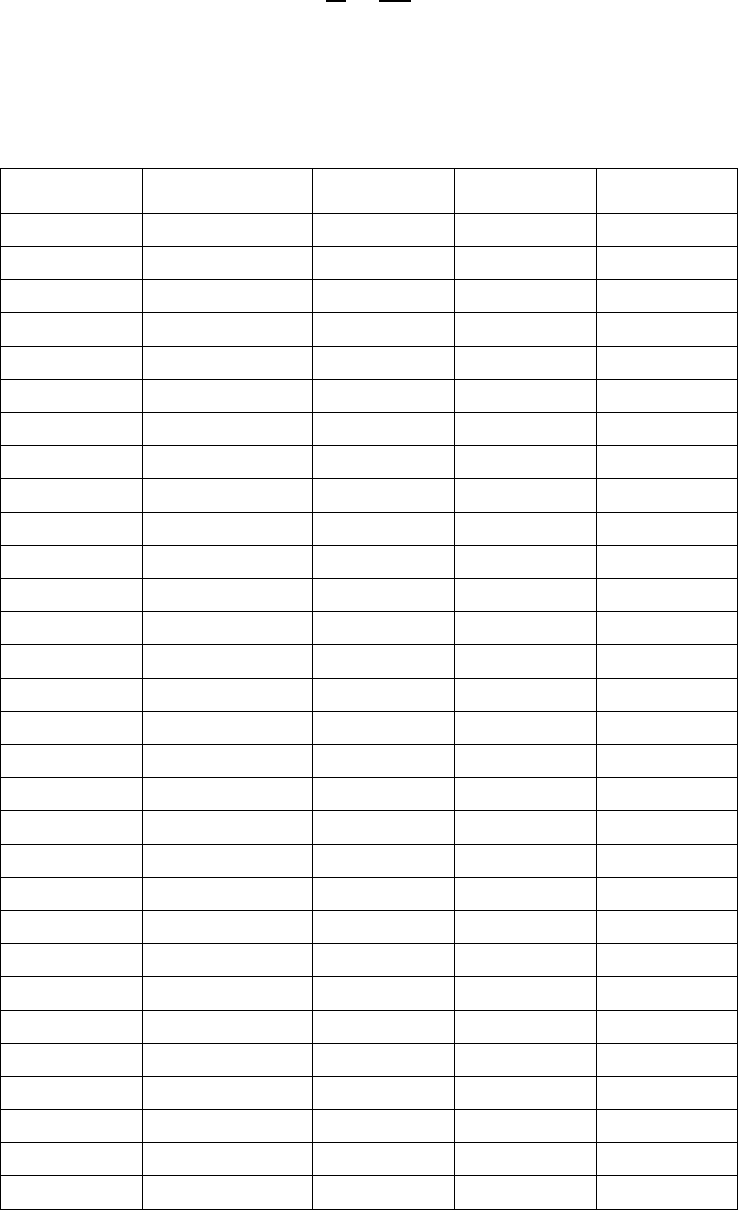
108
1) Упорядочим наблюдения в соответствии с возрастанием значений век-
тора .
2
X
2) Требуется отбросить
c наблюдений, содержащихся в середине массива
данных. Т.к. , то по формуле
30n =
4
15
c
n
=
получаем, что . Данные примут вид (табл. 2):
8c =
Табл.2. Упорядоченные данные задачи
№
y
1
x
2
x
3
x
2 1,41 0,74 0,05 18,13
16 5,39 0,8 0,15 14,42
25 -5,76 0,65 0,16 26,05
14 1,9 0,79 0,21 15,98
21 -3,76 0,62 0,23 30,53
26 -2,78 0,66 0,24 26,2
15 1,43 0,77 0,25 18,27
3 -2,79 0,66 0,29 25,74
19 1 0,76 0,32 19,35
22 1,12 0,75 0,32 17,98
5 -2,24 0,68 0,41 22,97
1
10
4
11
22
28
7
27
6 1,41 0,77 0,62 16,38
29 0,5 0,75 0,63 19,7
17 -2,3 0,71 0,66 22,76
18 1,42 0,79 0,74 15,41
24 0,55 0,74 0,75 18,29
12 1,55 0,78 0,77 15,06
20 0,91 0,78 0,89 16,83
30 0,61 0,75 1,1 16,87
13 0,09 0,72 1,2 17,6
9 1,18 0,81 1,31 13,38
8 0,36 0,78 1,76 14,48
109
3) Построим две эконометрические модели на основе 1МНК по двум об-
разованным совокупностям наблюдений объёмом
1
11n
=
и . Этот объ-
ём превышает общее количество независимых переменных , что и требу-
ется для теста. Имеем следующие модели:
2
11n =
3m =
1) ;
12
32,90009 46, 2564 1, 734991 0,013227yxx=− + − −
3
x
3
x
2) .
12
16,57204 6,7803 1,855062 0,53462yxx=−− −
4) Найдём сумму квадратов остатков и для первой и второй моде-
лей, соответственно:
1
S
2
S
1
12,3884S = ;
2
1, 29704S
=
.
5) Вычислим критерий , разделив большую сумму квад-
ратов остатков на меньшую. Для степеней свободы
*
9,551327R =
1
8k
=
, и выбранно-
го уровня значимости
2
8k =
0, 05
α
= определим табличное значение критерия Фи-
шера .
3, 4381
t
F =
Т.к. гетероскедастичность имеет место с надёжностью не менее
95%.
*
t
R> F
Т.о. оба метода исследования – критерий
μ
и параметрический тест
Гольдфельда-Квандта – привели к одинаковым выводам.
