Полшков Ю.Н. Курс лекций по экономико-математическому моделированию
Подождите немного. Документ загружается.


80
11 2 2
2
11 1 2 12 1
2
21 122 2 2
,
,
.
na b x b x y
axb x b xx yx
axb xxb x yx
⎧
++ =
⎪
⎪
++=
⎨
⎪
++ =
⎪
⎩
∑
∑∑
∑∑ ∑∑
∑∑ ∑∑
МНК применим и к уравнению множественной регрессии в стандартизи-
рованном масштабе:
12
12
... ,
m
yx x mx
tt t t
β
ββ
=+ ++ +
ε
где – стандартизированные переменные:
1
, , ...,
m
yx x
tt t
y
y
yy
t
σ
−
= ,
i
i
i
x
x
i
x
x
t
σ
−
=
, для которых среднее значение равно нулю: 0
i
yx
tt==, а среднее
квадратическое отклонение равно единице:
1
yx
i
tt
σ
σ
=
= ;
i
β
– стандартизиро-
ванные коэффициенты регрессии.
Стандартизованные коэффициенты регрессии показывают, на сколько
единиц изменится в среднем результат, если соответствующий фактор
i
x
изме-
нится на одну единицу при неизменном среднем уровне других факторов. В си-
лу того, что все переменные заданы как центрированные и нормированные,
стандартизованные коэффициенты регрессии
i
β
можно сравнивать между со-
бой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воз-
действия на результат. В этом основное достоинство стандартизованных коэф-
фициентов регрессии в отличие от коэффициентов «чистой» регрессии, кото-
рые несравнимы между собой.
Применяя МНК к уравнению множественной регрессии в стандартизиро-
ванном масштабе, получим систему нормальных уравнений вида
11213
212 13 1
123
123
123
12 3
... ,
... ,
........................................................
... ,
m
m
mm mm
yx xx xx m xx
yx x x x x m x x
yx x x x x x x m
rrr
rr r r
rr r r
βββ β
βββ β
ββ β β
=++++
⎧
⎪
=++++
⎪
⎨
⎪
⎪
=+ +++
⎩
1
r
где и
i
yx
r
ij
x
x
r – коэффициенты парной и межфакторной корреляции.
Коэффициенты «чистой» регрессии связаны со стандартизованными
коэффициентами регрессии
i
b
i
β
следующим образом:
i
y
ii
x
b
σ
β
σ
= . Поэтому
можно переходить от уравнения регрессии в стандартизованном масштабе к
уравнению регрессии в натуральном масштабе переменных, при этом параметр
определяется как
a
11 2 2
...
mm
aybxbx bx=− − −− .

81
Рассмотренный смысл стандартизованных коэффициентов регрессии по-
зволяет их использовать при отсеве факторов – из модели исключаются факто-
ры с наименьшим значением
i
β
.
3. На основе линейного уравнения множественной регрессии могут быть най-
дены частные уравнения множественной линейной регрессии.
Это уравнения регрессии, которые связывают результативный признак с
соответствующим фактором
i
x
при закреплении остальных факторов на сред-
нем уровне, т.е.
12 3
21 3
12 1
, ,..., 1 1 2 2 3 3
, ,..., 1 1 2 2 3 3
, ,..., 1 1 2 2 3 3
... ,
... ,
........................................................................
..
m
m
mm
xx x x m m
xxx x m m
xxx x
yabxbxbxbx
yabxbxbxbx
yabxbxbx
ε
ε
−
⋅
⋅
⋅
=+ + + ++ +
=+ + + ++ +
=+ + + +..
mm
bx
ε
⎧
⎪
⎪
⎨
⎪
⎪
+
+
⎩
При подстановке в эти уравнения средних значений соответствующих
факторов они принимают вид парных уравнений линейной регрессии:
12 3
21 3
12 1
, ,..., 1 1 1
, ,..., 2 2 2
, ,...,
,
,
................................
,
m
m
mm
xx x x
xxx x
x
xx x m m m
yAbx
yAb
yA
−
⋅
⋅
⋅
=+
⎧
⎪
=+
⎪
⎨
⎪
⎪
=+
⎩
x
bx
где
12233
21133
11 2 2 3 3 1 1
... ,
... ,
..............................................
... .
mm
mm
mm
Aabxbx bx
Aabxbx bx
m
A
abx bx bx bx
−
−
=+ + ++
⎧
⎪
=+ + ++
⎪
⎨
⎪
⎪
=+ + + ++
⎩
В отличие от парной регрессии частные уравнения регрессии характери-
зуют изолированное влияние фактора на результат, ибо другие факторы закре-
плены на неизменном уровне. Это позволяет определять частные коэффициен-
ты эластичности:
12 1 1
,,... , ,...,
x
i
iii
i
yi
m
x
xx x x x
x
Э b
y
−+
⋅
=⋅ ,
где – коэффициент регрессии для фактора
i
b
i
x
в уравнении множественной
регрессии,
12 1 1
, ,... , ,...,
iiim
x
xx x x x
y
−+
⋅
– частное уравнение регрессии.
Наряду с частными коэффициентами эластичности могут быть найдены
средние по совокупности показатели эластичности:
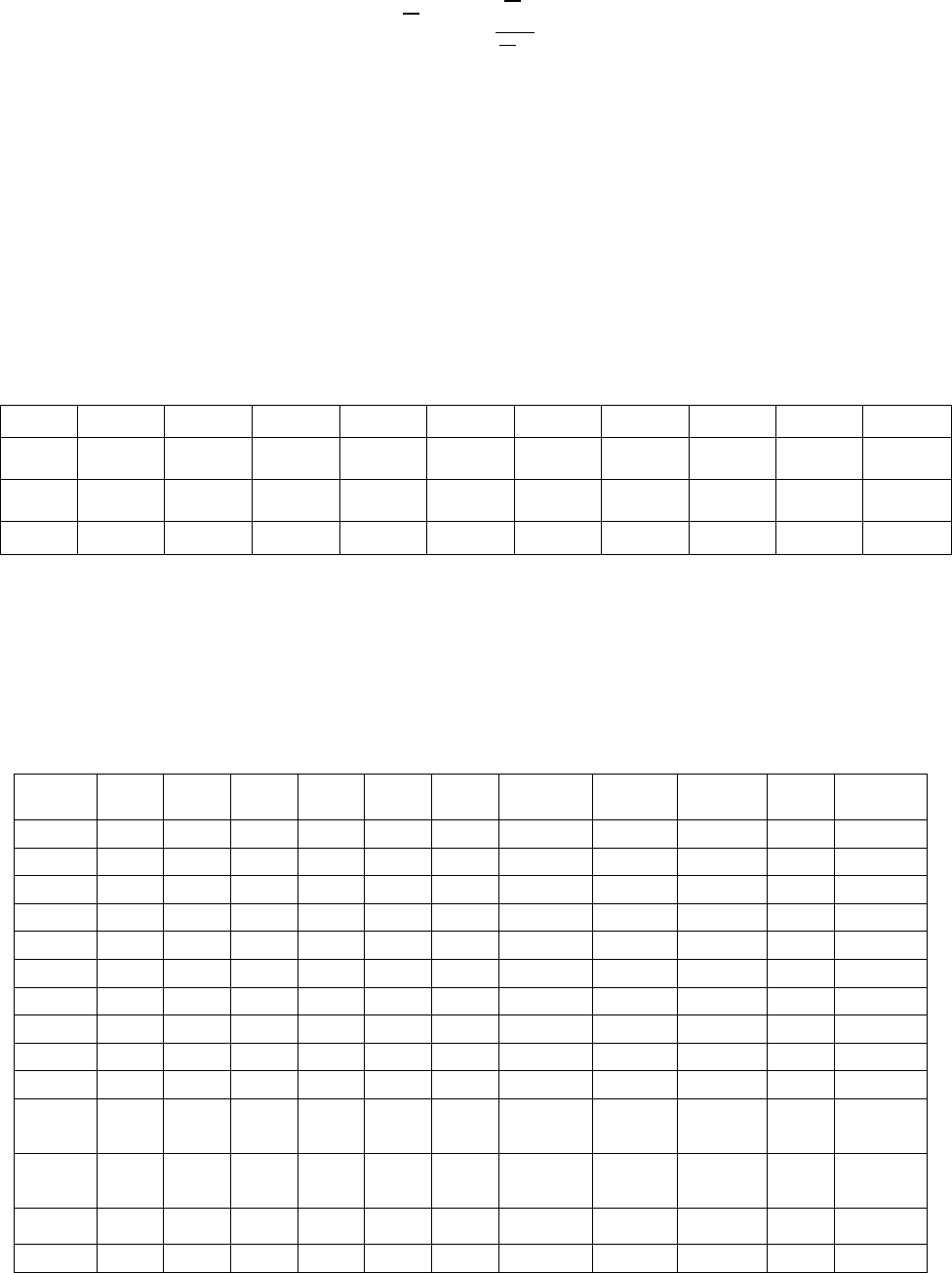
82
i
i
ii
x
x
Э b
y
=
⋅ ,
которые показывают на сколько процентов в среднем изменится результат, при
изменении соответствующего фактора на 1%. Средние показатели эластичности
можно сравнивать друг с другом и соответственно ранжировать факторы по си-
ле их воздействия на результат.
4. Рассмотрим пример построения линейной модели множественной регрессии.
Пример 1. Имеются данные о сменной добыче угля на одного рабочего
(т), мощности пласта
y
1
x
(м) и уровне механизации работ
2
x
(%), характери-
зующие процесс добычи угля в 10 шахтах.
Табл. 1. Данные примера 1
№ 1 2 3 4 5 6 7 8 9 10
1
x
8 11 12 9 8 8 9 9 8 12
2
x
5 8 8 5 7 8 6 4 5 7
y
5 10 10 7 5 6 6 5 6 8
Предполагая, что между переменными , y
1
x
,
2
x
существует линейная за-
висимость, требуется найти уравнение регрессии по
y
1
x
и
2
x
. Провести эко-
нометрический анализ полученной модели.
Решение. Составим вспомогательную табл. 2 (
x
yy
ε
=
−
).
Табл. 2. Расчёты по примеру 1
№
1
x
2
x
y
2
1
x
2
2
x
2
y
12
x
x
⋅
1
x
y
⋅
2
x
y⋅
x
y
2
ε
1 8 5 5 64 25 25 40 40 25 5,13 0,016
2 11 8 10 121 64 100 88 110 80 8,79 1,464
3 12 8 10 144 64 100 96 120 80 9,64 0,127
4 9 5 7 81 25 49 45 63 35 5,98 1,038
5 8 7 5 64 49 25 56 40 35 5,86 0,741
6 8 8 6 64 64 36 64 48 48 6,23 0,052
7 9 6 6 81 36 36 54 54 36 6,35 0,121
8 9 4 5 81 16 25 36 45 20 5,61 0,377
9 8 5 6 64 25 36 40 48 30 5,13 0,762
10 12 7 8 144 49 64 84 96 56 9,28 1,631
Сум-
ма
94 63 68 908 417 496 603 664 445 68 6,329
Ср.
знач.
9,4 6,3 6,8 90,8 41,7 49,6 60,3 66,4 44,5 – –
2
σ
2,44 2,01 3,36 – – – – – – – –
σ
1,56 1,42 1,83 – – – – – – – –
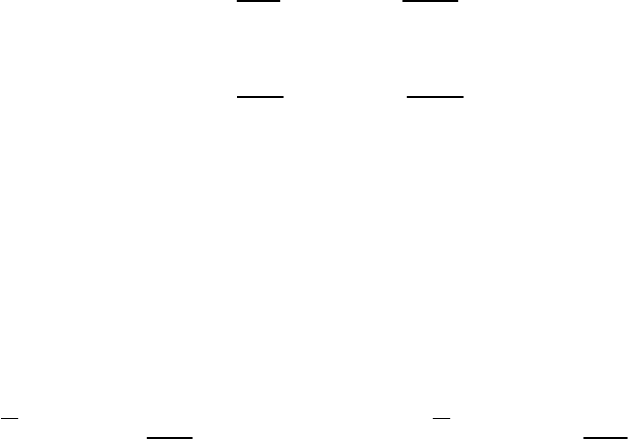
Для нахождения параметров уравнения регрессии решим следующую си-
стему нормальных уравнений:
83
12
12
12
10 94 63 68,
94 908 603 664,
63 603 417 445.
abb
ab b
ab b
+
+=
⎧
⎪
++ =
⎨
⎪
++ =
⎩
Откуда получаем, что
3, 54a
=
− ,
1
0,854b
=
,
2
0,367b
=
. Линейное
уравнение множественной регрессии имеет вид:
12
3,54 0,854 0,367
x
yx=− + ⋅ + ⋅x
.
Оно показывает, что при увеличении только мощности пласта
1
x
(при не-
изменном
2
x
) на 1 м добыча угля на одного рабочего увеличится в среднем
на 0,854 т, а при увеличении только уровня механизации работ
y
2
x
(при неиз-
менном
1
x
) на 1% – увеличится в среднем на 0,367 т.
Найдем уравнение множественной регрессии в стандартизованном мас-
штабе:
12
12yx x
tt t
β
β
=+ +
ε
. При этом стандартизованные коэффициенты рег-
рессии равны:
1
11
1, 56
0,854 0,728
1, 83
x
y
b
σ
β
σ
==⋅=;
2
22
1, 42
0,367 0,285
1, 83
x
y
b
σ
β
σ
==⋅=.
Т.е. уравнение будет выглядеть следующим образом:
12
0,728 0,285
y
x
x
ttt=⋅+⋅
.
Т.к. стандартизованные коэффициенты регрессии можно сравнивать ме-
жду собой, то можно сказать, что мощность пласта оказывает большее влияние
на сменную добычу угля, чем уровень механизации работ.
Сравнивать влияние факторов на результат можно также при помощи
средних коэффициентов эластичности:
1
9, 4
0,854 1,18
6,8
Э =⋅=
,
2
6,3
0,367 0,34
6,8
Э =⋅=
.
Т.е. увеличение только мощности пласта (от своего среднего значения)
или только уровня механизации работ на 1% увеличивает в среднем сменную
добычу угля на 1,18% или 0,34%, соответственно. Т.о., подтверждается боль-
шее влияние на результат фактора
y
1
x
, чем фактора
2
x
.
84
Лекция 5
МАТРИЧНАЯ ФОРМА ЛИНЕЙНОЙ МОДЕЛИ МНОЖЕСТВЕННОЙ
РЕГРЕССИИ
План лекции
1. Теорема Гаусса-Маркова.
2. Оператор оценивания 1МНК.
3. Ковариационная матрица оценок параметров эконометрической мо-
дели. Алгоритм пошагового регрессионного анализа.
1. Ранее была рассмотрена линейная модель множественной регрессии:
11 2 2
...
mm
yabxbx bx
ε
=+ + ++ +
.
При построении такой модели предполагают, что выполняются следую-
щие гипотезы:
1. Спецификация модели:
11 2 2
...
iiimim
yabxbx bx
i
ε
=+ + ++ +,
где – номер наблюдения.
1,...,i= n
m
2. Числовые значения независимых переменных
12
, ,...,
ii i
x
xx
являются
детерминированными (не случайными) величинами. Векторы
1
2
...
j
j
j
nj
x
x
x
x
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎝⎠
,
1,...,jm
=
линейно независимы в пространстве .
n
R
3. Случайные величины
i
ε
удовлетворяют условиям. Их математические
ожидания равны нулю:
() 0
i
M
ε
=
. Дисперсии:
2
() ( )
ii
DM
2
ε
εσ
=
= . Причём
значения математических ожиданий и дисперсий ошибок не зависят от номера
наблюдений
i.
4. При
k ковариации ошибок равны нулю: l≠
cov( , ) ( ) 0
kl k l
M
ε
εεε
=
⋅=
,
т.е. для разных наблюдений имеет место статистическая независимость (некор-
релированность) ошибок.
5 (дополнительная гипотеза). Ошибки
i
ε
являются нормально распреде-
лёнными случайными величинами со средним и дисперсией
0
2
σ
:
2
(0, )
i
N
ε
σ
∼ .
Заметим, что при выполнении гипотез 1 – 5 эконометрическая модель на-
зывается нормальной линейной регрессионной моделью.
Важнейшую роль в эконометрическом анализе играет следующая теоре-
ма, формулировка которой приводится без доказательства.
85
Теорема Гаусса-Маркова. Предположим, что для линейной модели
множественной регрессии выполняются гипотезы 1 – 4. Тогда оценки коэффи-
циентов регрессии , найденные с помощью МНК, являются наи-
более эффективными (в смысле наименьшей дисперсии) среди всех линейных
несмещённых оценок.
12
,,,...,
m
ab b b
Заметим, что при невыполнении отдельных гипотез теорема Гаусса-
Маркова становится неприменимой. Следовательно, и МНК не будет давать
достоверных результатов.
Например, нарушение условия линейной независимости векторов
j
x
(ги-
потеза 2) приводит к нежелательному явлению, называемому мультиколлине-
арностью. Условие независимости дисперсии ошибок от номера наблюдения
(гипотеза 3) называется гомоскедастичностью. Нарушение данного условия
называют гетероскедастичностью. Невыполнение гипотезы 4 называется ав-
токорреляцией ошибок.
В дальнейшем будут предложены методы выявления мультиколлинеар-
ности, гетероскедастичности и автокорреляции ошибок, а также способы по-
строения эконометрических моделей при наличии этих нежелательных явле-
ний.
2. В силу большого числа наблюдений и наличия нескольких переменных ли-
нейную модель множественной регрессии удобно записывать в матричном ви-
де.
Пусть – вектор значений зависимой переменной размерности
Y
1n
×
;
– матрица независимых переменных размерности
X
(1nm)
×
+ (n – число на-
блюдений, – количество независимых переменных); – вектор параметров
модели размерности
(1;
m B
)1
ε
– вектор остатков размерности : 1nm +× ×
1
2
...
n
y
y
Y
y
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
;
11 12 1
21 22 2
12
1...
1...
... ... ... ... ...
1...
m
m
nn nm
x
xx
x
xx
X
x
xx
⎛⎞
⎜⎟
⎜⎟
⎟
=
⎜
⎜⎟
⎝⎠
1
...
m
a
b
B
b
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
; ;
1
2
...
n
ε
ε
ε
ε
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
.
Заметим, что наличие в матрице столбца из единиц обусловлено ана-
литическим видом модели:
X
11 2 2
...
mm
yabxbx bx
ε
=+ + ++ +,
которая содержит свободный член .
a
Линейная эконометрическая модель в матричной форме имеет вид
YXB
ε
=
+ .
Оценим с помощью МНК вектор параметров . Представим матричное
уравнение в виде:
B
YXB
ε
=−
. Тогда сумму квадратов остатков можно запи-
сать так:

86
2/ / / // //
1
()() 2
n
i
i
Y XB Y XB YY BXY BXXB
εεε
=
==− − = − +
∑
,
где «штрих» обозначает операцию транспонирования матрицы.
Продифференцируем это выражение по и приравняем производную к
нулю:
B
()
/
//
22XY XXB 0
B
εε
∂
=
−+ =
∂
.
Имеем матричную форму системы линейных нормальных уравнений:
//
()XXB XY= .
Таким образом, получим оператором оценивания 1МНК:
(
)
1
//
BXXX
−
= Y
,
который получил своё название от т.н. одношагового МНК.
3. Важное прикладное значение имеет нахождение ковариационной матрицы
оценок параметров эконометрической модели.
Эта матрица используются для нахождения стандартных ошибок, вычис-
ления доверительных интервалов оценок параметров и при проверке их стати-
стической значимости. Формула для её нахождения следующая:
(
)
(
)
2
1
/
var BX
ε
σ
X
−
=⋅
,
где
2
ε
σ
– несмещенная оценка дисперсии остатков:
()
/
/
//
2
11
YY BXY
nm nm
ε
εε
σ
−
==
−
−−−
.
На главной диагонали ковариационной матрицы расположены оценки
дисперсий регрессионных коэффициентов, вне её – оценки ковариаций:
()
()
(
)
(
)
()
()
()
()
()
()
()
()
()
()
()
()
()
2
12
2
11121
2
2212 2
2
12
, , ... ,
, , ... ,
var
, , ... ,
... ... ... ... ...
, , , ...
m
m
m
mm m
aabab ab
ba b bb bb
B
ba bb b bb
ba bb bb b
σσ σ σ
σσσ σ
σσ σ σ
σσ σ σ
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
m
.
Для проверки значимости коэффициентов регрессии их величины
сравниваются с их стандартными ошибками, которые вычисляются как квад-

87
ратный корень из соответствующего элемента главной диагонали матрицы
. Определяются фактические значения
t
-критерия Стьюдента:
()
var B
()
()
a
ta
a
σ
= ;
()
()
j
j
j
b
tb
b
σ
=
, 1, 2,...,jm
=
,
которые затем сравниваются с табличным значением
(
табл
;t
)
k
α
при уровне
значимости
α
и числе степеней свободы
1knm
=
−−
. Если
()
табл
() ;
j
tb t k
α
>
,
то говорят, что оценка коэффициента регрессии
j
b
статистически значима с
надёжностью не менее
1
α
− .
В противном случае оценка коэффициента регрессии
j
b
незначима. Сле-
довательно, независимая переменная
j
x
должна быть исключена из модели.
После этого снова находят оператор оценивания 1МНК, ковариационную мат-
рицу
()
var B и т.д.
Эта процедура повторяется до тех пор, пока все оценки коэффициентов
регрессии не будут статистически значимыми. Такой подход называют алго-
ритмом пошагового регрессионного анализа. При этом мы получаем уравне-
ние регрессии с максимальным числом значимых коэффициентов. Заметим, что
свободный член
a обычно не проверяется на статистическую значимость.
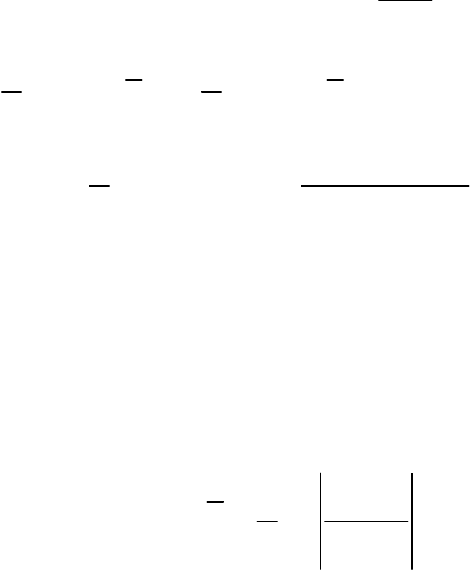
Для значимых коэффициентов регрессии принято находить доверитель-
ные интервалы оценок параметров:
()
(
)
()
()
табл табл
;;at k a aat k a
ασ ασ
−⋅≤≤+⋅,
()
()
()
(
)
табл табл
;;
j
jj j
j
bt k b bbt k b
ασ ασ
−⋅≤≤+⋅
1,2,...,jm=, .
88
Лекция 6
ОСОБЕННОСТИ МНОГОФАКТОРНЫХ ЛИНЕЙНЫХ
ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
План лекции
1. Теснота связи факторов в уравнении множественной линейной рег-
рессии. Проверка значимости.
2. Построение прогноза с помощью эконометрической модели.
3. Пример построения эконометрической модели в матричном виде.
1. Практическая значимость уравнения множественной регрессии оценивается с
помощью показателя множественной корреляции и его квадрата – показателя
детерминации.
Множественный коэффициент детерминации вычисляется по форму-
ле:
2
2
ост
2
1
y
R
σ
σ
=− ,
где
()
2
2
11
y
yy y y
nn
σ
=−=−
∑∑
22
– общая дисперсия результативного
признака;
()
l
/
//
2
2
ост
1
x
YY BXY
yy
nn
σ
−
=−=
∑
– остаточная дисперсия. Он
характеризует долю дисперсии результативного признака , объясняемую рег-
рессией, в общей дисперсии результативного признака. Следовательно, вели-
чина характеризует долю дисперсии , вызванную влиянием остальных,
не учтённых в модели, факторов.
y
2
1 R− y
Чтобы иметь общее суждение о качестве модели из относительных от-
клонений по каждому наблюдению, определяют среднюю ошибку
аппроксимации:
1
100%
x
yy
A
ny
−
=⋅
∑
.
Считается, что средняя ошибка аппроксимации не должна превышать 8–10%.
Множественный коэффициент корреляции характеризует тесноту
связи рассматриваемого набора факторов с исследуемым признаком. Границы
изменения коэффициента множественной корреляции от 0 до 1. Чем ближе его
значение к 1, тем теснее связь результативного признака со всем набором ис-
следуемых факторов.
R
Скорректированный множественный коэффициент детерминации
содержит поправку на число степеней свободы, а именно остаточная сумма
квадратов делится на число степеней свободы остаточной вариа-
(
2
x
yy−
∑
)

89
ции , а общая сумма квадратов отклонений
(
1nm−−
)
(
2
yy−
)
∑
на число
степеней свободы в целом по совокупности
(
)
1n
−
:
l
()
()
()()
()
2
2
2
2
1
1
111
1
1
x
yy nm
n
RR
nm
yy n
−−−
−
=− =− − ⋅
−−
−−
∑
∑
,
где – число параметров при переменных
m
x
; – число наблюдений.
n
Значимость уравнения множественной регрессии в целом оценивается
с помощью -критерия Фишера:
F
2
факт
2
ост
1
1
S
Rnm
F
SRm
−
−
== ⋅
−
,
где – факторная сумма квадратов на одну степень свободы; – оста-
точная сумма квадратов на одну степень свободы; – множественный коэф-
фициент детерминации.
факт
S
ост
S
2
R
Фактическое значение -критерия сравнивается с табличным значением
F
(
табл 12
;;Fk
)
k
α
при уровне значимости
α
и степенях свободы
1
km
=
и
. При этом, если
2
1knm=− −
(
)
табл 12
;;FF kk
α
> ,
то говорят, что найденное уравнение регрессии статистически значимо с на-
дёжностью не менее
1
α
− . В противном случае оно незначимо.
Для проверки значимости множественного коэффициент корреляции
определяется фактическое значение
t-критерия Стьюдента:
l
l
2
1
1
Rn m
t
R
−
−
=
−
,
которое затем сравнивается с табличным значением
(
)
табл
;tk
α
при уровне
значимости
α
и числе степеней свободы
1knm
=
−−
. Если
(
)
табл
;tt k
α
> ,
то говорят, что множественный коэффициент корреляции статистически зна-
чим с надёжностью не менее
1
α
− . В противном случае он незначим.
2. При наличии регрессионной модели исследователь может строить точечные
и интервальные прогнозы относительно зависимой переменной .
y
Для построения прогноза надо располагать вектором предполагаемых
значений независимых факторов, входящих в модель:
