Понетаева Н.Х., Патрушева Н.В. Начертательная геометрия в примерах и задачах
Подождите немного. Документ загружается.

89
2. Плоскость
α
пересекает поверхность Ф по кольцу радиусом (R – R*).
3. Отрезок AB пересекается с сечением в точках M и N, которые являются искомыми точками
пересечения отрезка с поверхностью тора.
4. В горизонтальной проекции точка М
]
видна, поскольку расположена над экватором тора, точка N
1
не видна. Во фронтальной проекции точки M
2
и N
2
невидны, они расположены на задней части
поверхности.
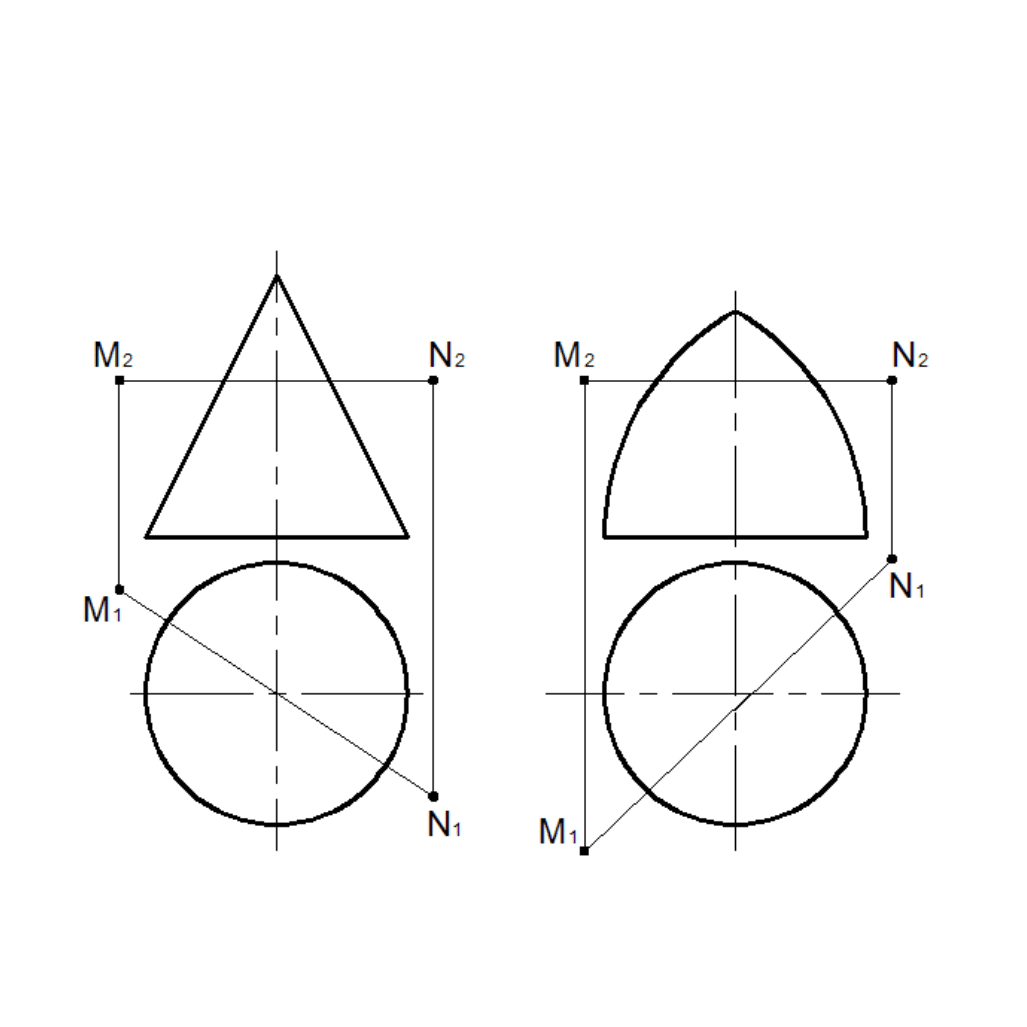
Задачи 5.19, 5.20
Построить проекции точек пересечения отрезка MN с поверхностями конуса и закрытого тора.
Определить видимость отрезка.
Рис. 5.26 Рис. 5.27
90
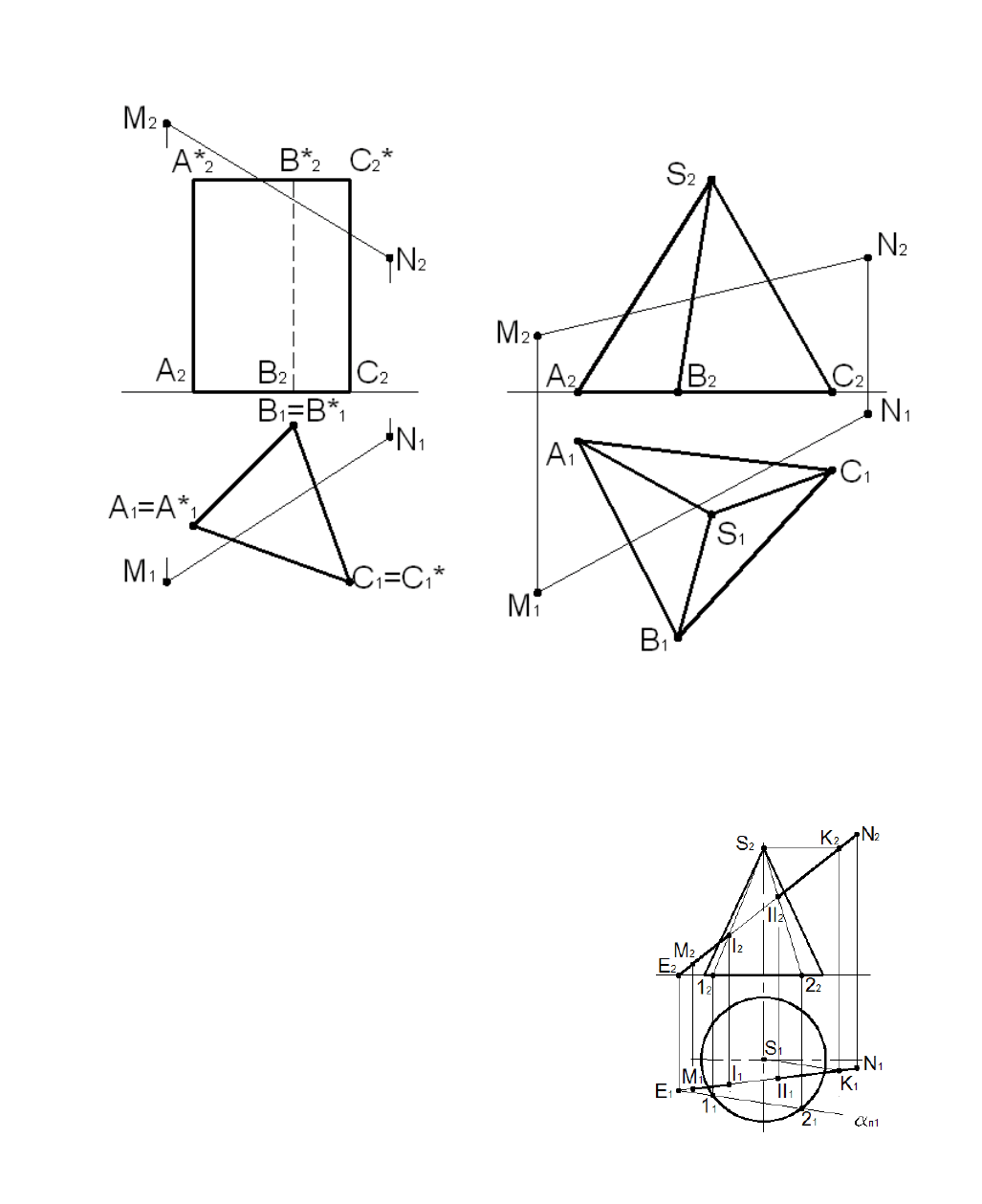
Задачи 5.21, 5.22
Построить проекции точек пересечения отрезка MN с поверхностями призмы и пирамиды. Определить
видимость отрезка.
Рис. 5.28 Рис. 5.29
Пример 5.4
Построить проекции точек пересечения
отрезка MN общего положения с поверхностью
конуса. Определить видимость отрезка.
I, II = MN
∩ Φ – ?
1. Плоскость
α
– общего положения и задается
отрезком MN и горизонталью SK, K
∈ MN, след
α
П1
проходит через горизонтальный след MN
параллельно горизонтали SK,
E = MN
∩ П
1
, E ∈
α
П1
,
α
П1
‖ S
1
K
1
.
2.
α
П1
пересекается с основанием конуса в точках 1 и
2, через них проходят образующие конуса S – 1, S –
2, по которым пересекает поверхность конуса,
α
∩Φ = (S – 1, S – 2).
3. Отрезок прямой MN пересекается с образующими
конуса S – 1, S – 2 в точках I и II, которые являются
искомыми.
Рис.5.30
91
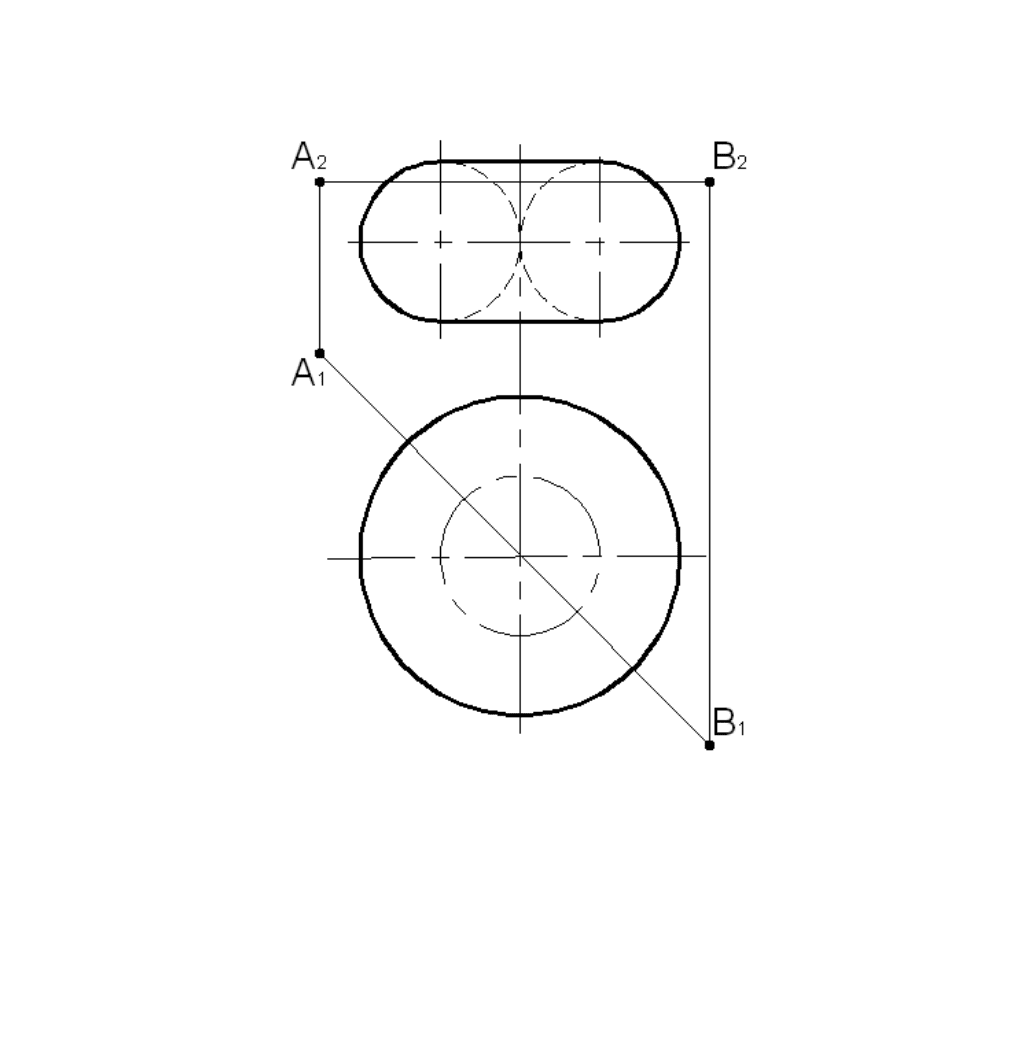
Задача 5.24
Построить проекции точек пересечения отрезка АВ с поверхностью тора. Определить видимость
отрезка.
Рис. 5.31
93
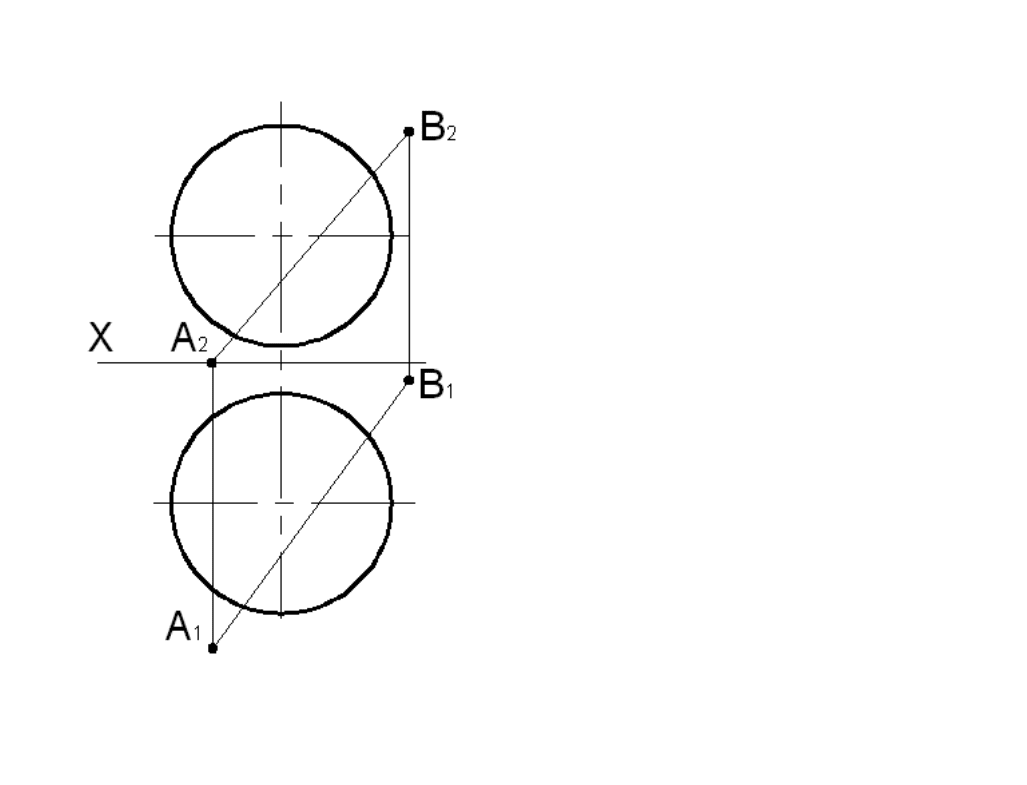
Задача 5.25
Построить проекции точек пересечения отрезка АВ с поверхностью сферы. Определить видимость
отрезка. Решить способом замены плоскостей проекций.
Рис. 5.32

94
Для самостоятельной работы
95
6. Взаимное пересечение поверхностей
6. 1 Способы построения линии пересечения поверхностей
Для построения линии пересечения поверхностей нужно найти общие точки, принадлежащие им, и
затем соединить их в определённой последовательности. Линией пересечения может быть:
• пространственная кривая – при пересечении кривых поверхностей или кривой поверхности и
многогранника;
• пространственная ломаная линия – при пересечении двух многогранников;
• плоская кривая – в частных случаях пересечения поверхностей.
Точки линии пересечения находят с помощью вспомогательных секущих плоскостей или
вспомогательных поверхностей – сфер, цилиндров, конусов.
6.2 Способ вспомогательных секущих плоскостей
Для определения произвольной точки линии пересечения:
• вводят вспомогательную секущую плоскость;
• находят линии пересечения этой плоскости с каждой поверхностью;
• на пересечении найденных линий получают искомые точки.
Вспомогательную секущую плоскость следует выбирать так, чтобы её линия пересечения с каждой
поверхностью проецировалась на плоскости проекций в виде простейших линий – прямой или окружности.
Линия пересечения имеет характерные точки, с которых нужно начинать построение. К таким точкам
относятся экстремальные точки – верхняя и нижняя точки относительно той или иной плоскости проекций;
точки, расположенные на очерковых образующих – точки видимости; точки наибольшей ширины кривой.
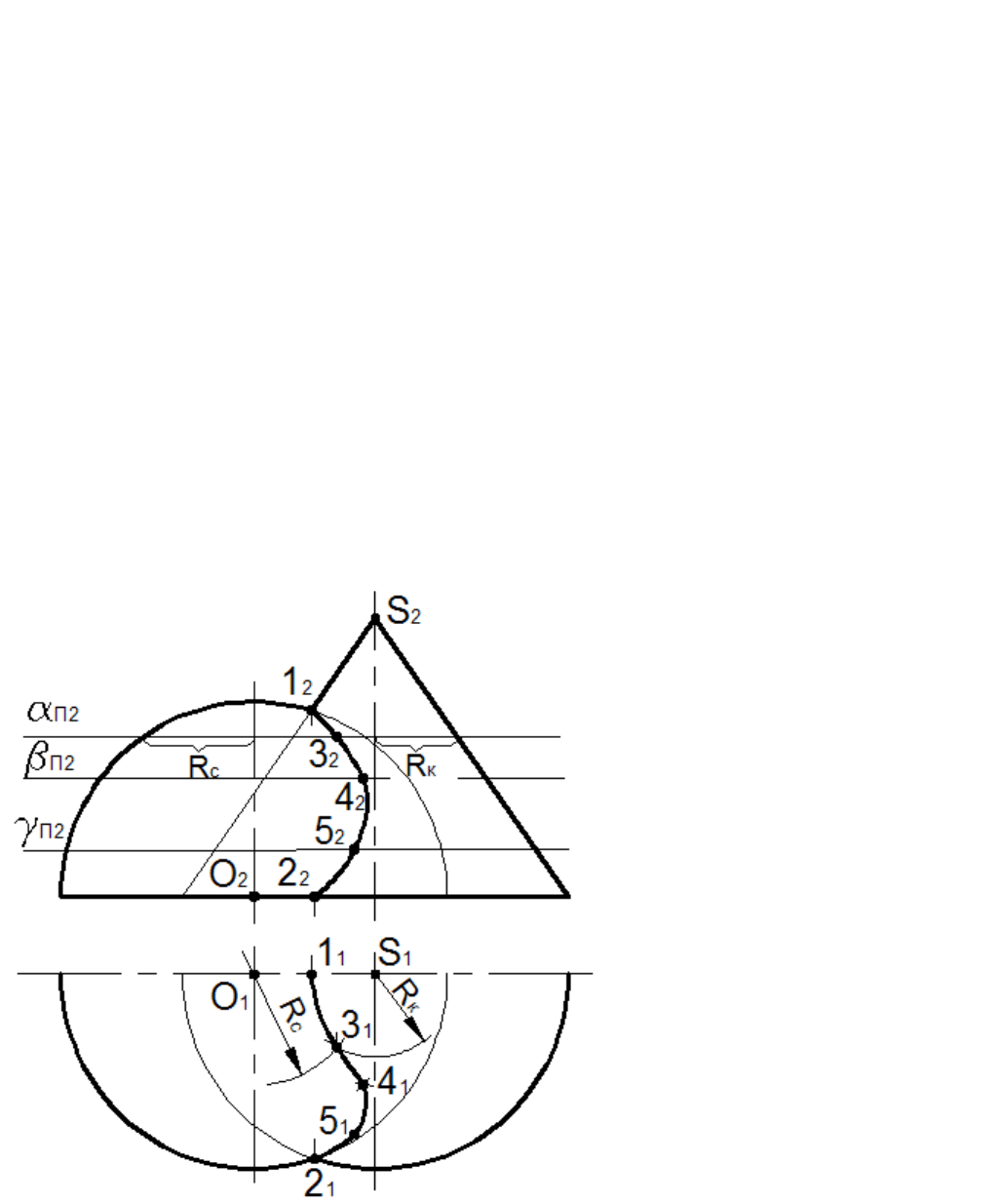
Пример 6.1
Построить проекции линии пересечения конуса с полусферой, экватором расположенным в П
1
.
Оси вращения поверхностей
расположены в одной плоскости,
параллельной П
2
Линия пересечения
имеет плоскость симметрии, поэтому
на горизонтальной проекции строится
половина изображения.
Высшая точка 1 построена как точка
пересечения главного меридиана
сферы с крайней левой образующей
конуса. Низшая точка 2 является
точкой пересечения экватора сферы с
основанием конуса.
Промежуточные точки 3, 4, 5
найдены с помощью вспомогательных
секущих горизонтальных плоскостей
уровня
α
,
β
и
γ
, проведенных
произвольно. Вспомогательная
плоскость
α
пересекает полусферу по
окружности радиуса R
C
, а конус – по
параллели радиуса R
K
. На пересечении
горизонтальных проекций этих
параллелей построена точка 3
1
.
Фронтальная проекция точки 3
2
принадлежит и
α
П2
. Точки 4, 5 пост-
роены аналогично точке 3.
Рис. 6.1
96
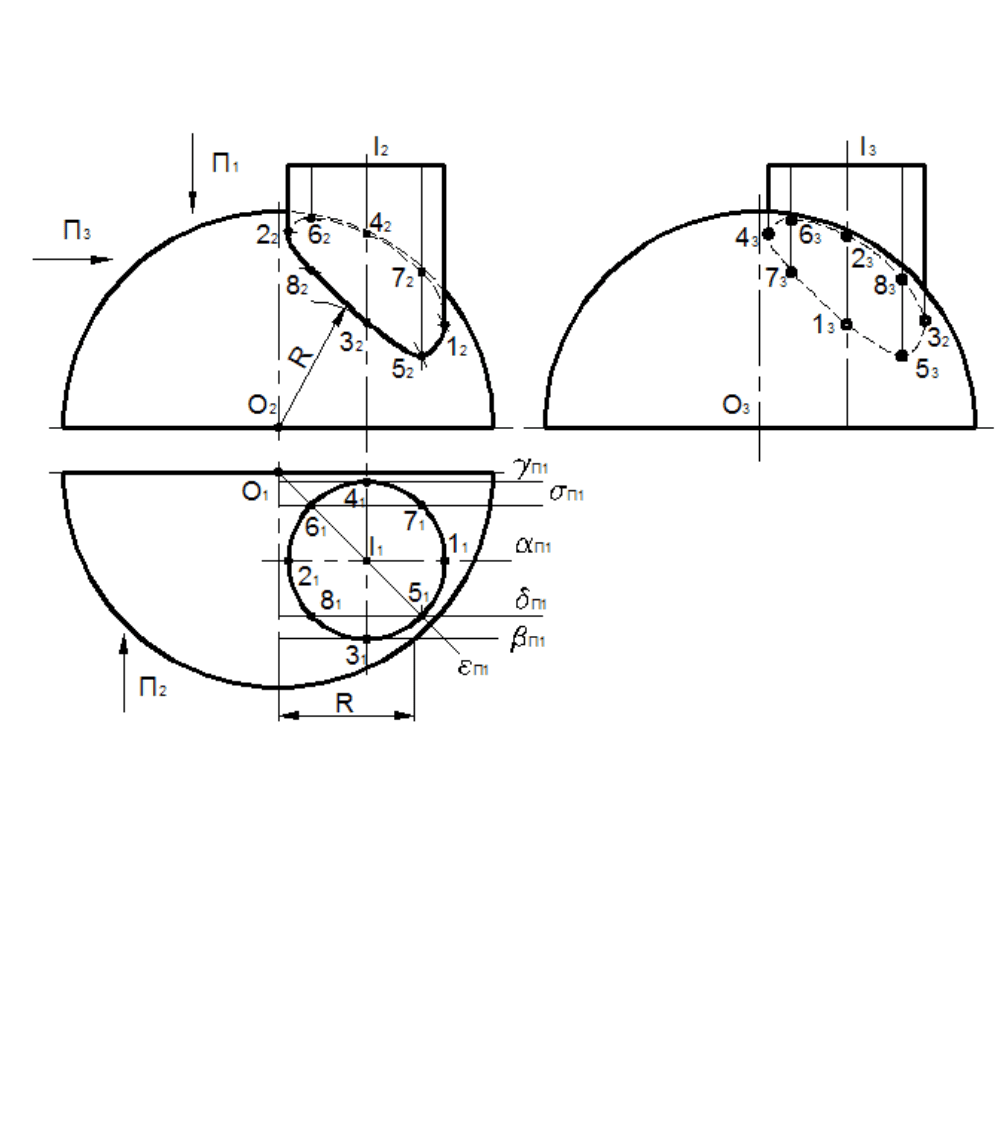
Пример 6.2
Построить проекции линии пересечения цилиндра вращения с полусферой, расположенной
экватором в горизонтальной плоскости проекций.
Рис. 6.2
Одна из поверхностей – цилиндр – является горизонтально проецирующей, образующие цилиндра
перпендикулярны П
1
. Проекция линии пересечения на П
1
определяется без дополнительных построений и
совпадает с очерком цилиндра.
Горизонтальные проекции характерных точек расположены на окружности основания цилиндра.
Вспомогательные секущие фронтальные плоскости уровня
α
П1
–
γ
П1
, проведённые через точки 1 – 8,
пересекают сферу по окружностям, а цилиндр – по линейным образующим. Высшая и низшая точки 5, 6
линии пересечения расположены в горизонтально проецирующей плоскости, проходящей через оси
цилиндра и сферы.
При определении видимости линии пересечения в плоскостях проекций поверхности цилиндра и
полусферы считаются непрозрачными.
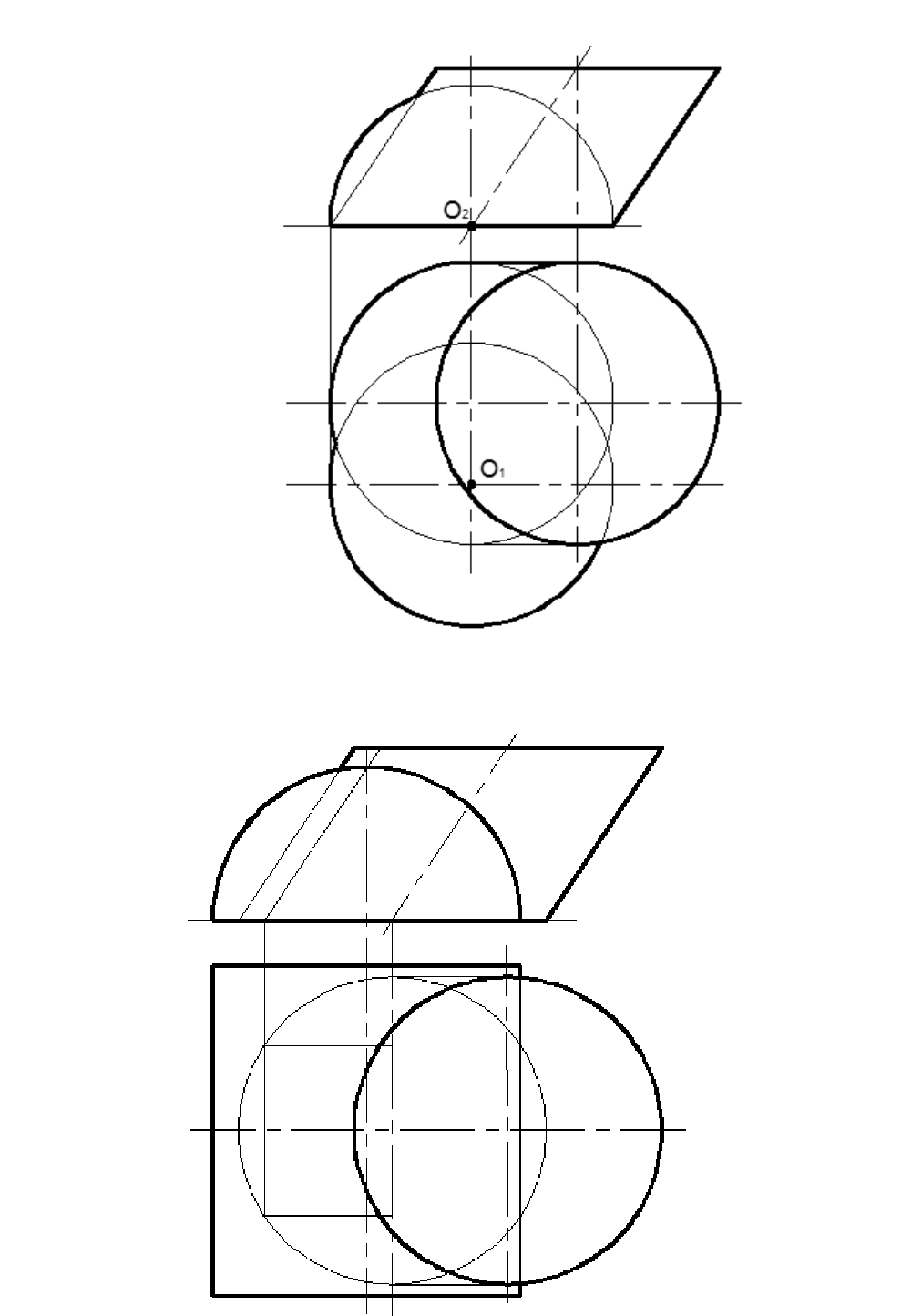
97
Задача 6.1
Построить проекции пинии пересечения наклонного цилиндра с полусферой.
Рис. 6.3
Задача 6.2
Построить проекции пинии пересечения наклонного цилиндра с половиной цилиндра.
Рис. 6.4
98
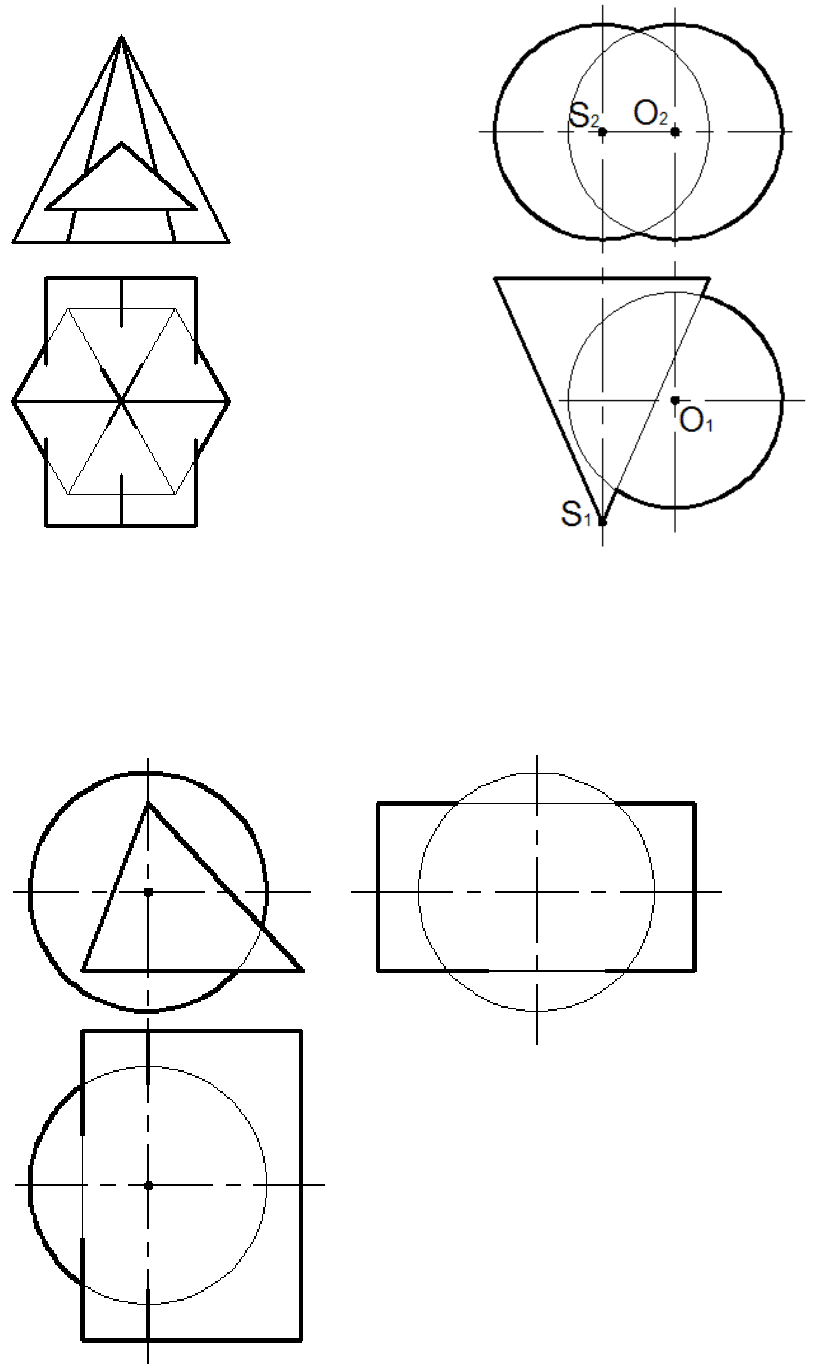
Задача 6.3
Построить проекции линии пересечения
пирамиды с призмой.
Задача 6.4
Построить проекции линии пересечения сферы с
конусом.
Рис. 6.5
Рис. 6.6
Задача 6.5
Построить проекции линии пересечения сечения сферы с призмой.
Рис. 6.7
99
Задача 6.3
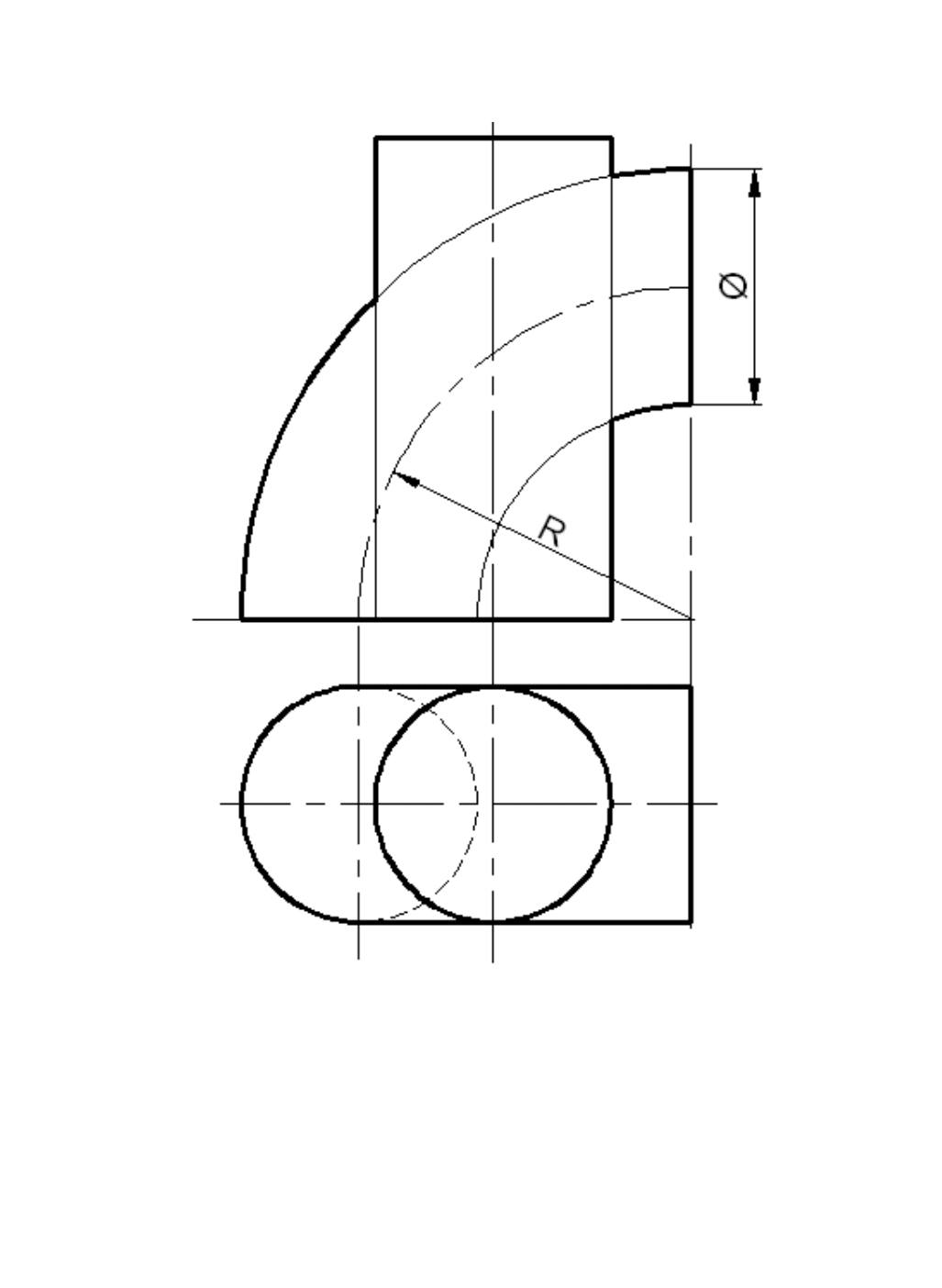
Построить проекции пинии пересечения цилиндра с тором.
Рис. 6. 8
