Пьянков В.П. Тексты лекций по элементарной математике
Подождите немного. Документ загружается.

В.П.Пьянков Избранные разделы элементарной математики
0),(
0),(
0)(
0),(
0),(
0)(
pf
pf
pA
pf
pf
pA
0),()(
0),()(
pfpA
pfpA
Этой системе равносильны условия задачи.
Как поступать, если в условии задачи присутствует полузамкнутый или замкнутый промежуток,
смотрите в замечании после пункта 2.4.
Пример. При каких значениях параметра а квадратное уравнение
xaax 31
2
имеет один
корень на промежутке
)0;(
, а другой на интервале (0; 2)?
Решение.
013
2
axax
. Обозначим
13)(
2
axaxxf
. Условию задачи эквивалентна система:
0)2(
0)0(
fa
fa
;
0)164(
0)1(
aaa
aa
;
0)1(5
0)1(
aa
aa
;
);1()0;(
)0;1(
a
a
Ответ:
)0;1(a
.
51
Совокупность этих систем можно
записать в виде одной системы:

В.П.Пьянков Избранные разделы элементарной математики
2.2. При каких значениях р уравнение
0),( pxf
имеет один корень на интервале
);(
,
другой на
);(
?
Для ответа на этот вопрос надо решить
систему
0)(
0)(
fA
fA
Как поступать, если в условии задачи присутствует замкнутый или полузамкнутый промежуток,
смотрите в замечании после пункта 2.4.
52
y
A>0
β
α
х
у
A<0
β
α
х
у

В.П.Пьянков Избранные разделы элементарной математики
2.3. При каких значениях р уравнение
0),( pxf
имеет один корень на интервале
);(
,
другой вне отрезка
];[
?
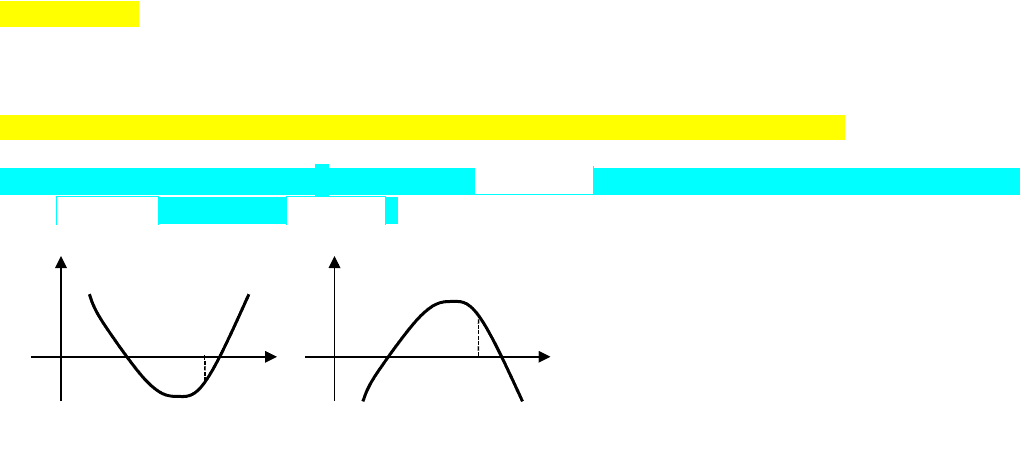
Этот случай характеризуется тем, что
)(
f
и
)(
f
имеют разные знаки
(посмотрите на четыре предыдущих рисунка), т.е.
0)()( ff
. Следует
добавить еще условие
0A
, т.к. в противном случае уравнение становится линейным и не может иметь
два корня. В результате получаем следующую систему:
Замечание. При решении этой задачи, а также задач пунктов 2.1 и 2.2, условие существования
корней, записанное через дискриминант, накладывать необязательно. Оно выполнится само по себе. Иначе
быть не может. Известна теорема Коши: если функция
)(xf
непрерывна на отрезке
];[
и значения
)(
f
и
)(
f
имеют разные знаки, т.е.
0)()(
ff
, то на интервале
);(
найдется такая точка
(по крайней мере, одна), что
0)(
f
.
Пример [4], №6.59. При каких значениях а корни уравнения
2
2
axax
будут действительны и
один корень по модулю будет больше 1, а другой по модулю меньше 1? Ответ:
);1( a
.
53
0)()(
0
ff
A
(*)
В.П.Пьянков Избранные разделы элементарной математики
2.4. При каких значениях р уравнение
0),( pxf
имеет один корень на интервале
);(
,
другой вне него?
Ни одна из парабол, удовлетворяющих условиям предыдущей задачи, не проходит через
точку
или
. Это принципиальное обстоятельство, на основе которого было получено 2-е
неравенство системы (*). Поэтому при решении задачи этого пункта надо рассмотреть три случая:
1) решить задачу пункта 2.3;
2) рассмотреть отдельно случай, когда один корень равен
;
3) рассмотреть отдельно случай, когда один корень равен
.
Пример. При каких значениях параметра, а квадратное уравнение
013
2
axax
имеет один
корень, принадлежащий интервалу (0;2), а другой, не принадлежащий ему?
Решение. 1) Рассмотрим случай, когда
]2;0[
1
x
,
)2;0(
2
x
:
0)2()0(
0
ff
a
;
0)164)(1(
0
aaa
a
;
0)1)(1(5
0
aa
a
;
)1;0()0;1( a
.
2) Рассмотрим случай, когда
0
1
x
.
Найдем при каком а это может быть:
01030
2
aa
;
01 a
;
1a
.
54
В.П.Пьянков Избранные разделы элементарной математики
Уравнение при этом приобретает вид:
0113
2
xx
;
03
2
xx
;
0)3( xx
.
)2;0(3
2
x
.
3) Случай, когда
2
1
x
:
1a
;
023
2
xx
;
)2;0(1
2
x
. Ответ:
]1;0()0;1( a
.
Пример. При каких значениях параметра а уравнение
013
2
axax
имеет на интервале (0; 2)
единственный корень? Ответ:
2/)110(]1;1( a
.
Примечания к последнему примеру.
1) Здесь условие
0a
не требуется, т.к. формулировка задачи допускает отсутствие второго корня.
2)
2/)110( a
соответствует случаю, когда квадратное уравнение имеет один (двукратный) корень,
принадлежащий интервалу (0;2):
0D
;
0)1(49 aa
;
0944
2
aa
;
2
101
4
402
a
;
aa
b
x
2
3
2
;
)2;0(
101
3
;
)2;0(
101
3
.
Замечание к пунктам 2.1 и 2.2.
Также, как и в пункте 2.4, случаи равенства корней числам
и (или)
надо рассматривать
(проверять) отдельно в задачах, подобных задачам пункта 2.1, но с замкнутым или полузамкнутыми
55
В.П.Пьянков Избранные разделы элементарной математики
промежутками вида:
];(
и
);(
, или
);(
и
);[
, или
);(
и
];(
,
или
);(
и
];[
, или
];(
и
];(
.
То же самое надо делать и в задачах пункта 2.2 с аналогичными изменениями в условиях.
3.1. При каких значениях р уравнение
0),( pxf
имеет один корень на промежутке
);(
, другой на
);(
?
Условию задачи равносильно неравенство
0)(
fA
56
A<0
α
х
у
A>0
α
х
у
В.П.Пьянков Избранные разделы элементарной математики
Пример [8], №16.175. Найти все значения а, при которых один корень уравнения
axaxa )32()1(
22
больше 1, а другой меньше 1. Ответ:
)2;1()1;1(
.
Замечание. Если в тексте примера «меньше» заменить словами «не больше» (т.е.
1
1
x
,
1
2
x
), то
ответ останется прежним. Если «больше» заменить словами «не меньше» (т.е.
1
1
x
,
1
2
x
), то ответом
будет
]2;1()1;1[ a
. В этих задачах значения параметра, при которых один корень равен , надо
рассматривать отдельно.
3.2. При каких значениях р уравнение
0),( pxf
имеет корни разных знаков?
Это частный случай предыдущего. Для него требуемое неравенство можно составить, используя
условие
ACxx /
21
теоремы Виета:
0/ AC
Отметим, что при этом получается
04
2
ACBD
.
Пример [8], №14.216. При каких значениях а график
3)5(
2
axxay
пересекает ось
абсцисс по разные стороны от оси ординат?
57

В.П.Пьянков Избранные разделы элементарной математики
Ответ:
)3;5(a
.
58
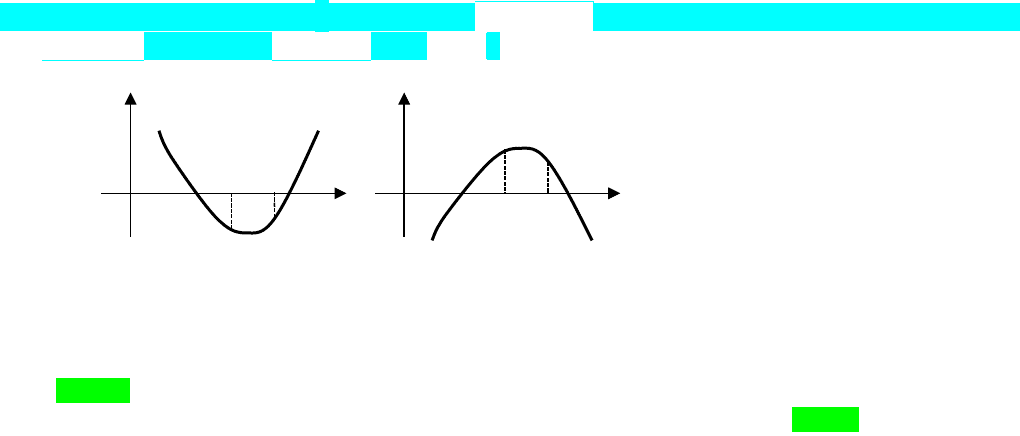
В.П.Пьянков Избранные разделы элементарной математики
3.3. При каких значениях р уравнение
0),( pxf
имеет один корень на промежутке
);(
, другой на
);(
, где
?
Условию задачи равносильна система
0)(
0)(
fA
fA
(**)
Пример [6], №211. При каких значениях параметра а один из корней уравнения
04)3(2)2(
2
axaxa
больше 3, другой меньше 2? Ответ:
)5;2(a
59
A<0
α β
х
у
A>0
α β
х
у

В.П.Пьянков Избранные разделы элементарной математики
Замечание. Если в условии задачи присутствует промежуток
];(
, то надо в 1-м неравенстве
системы (**) поставить знак «
»; если присутствует промежуток
);[
, то надо во 2-м неравенстве
поставить этот знак.
Пример [10], с.220. При каких значениях параметра а все решения неравенства
01
2
x
являются решениями неравенства
011
2
axx
?
Решение.
]1;1[01
2
xx
. Значит, отрезок
]1;1[
должен целиком лежать на отрезке, ограниченном корнями трехчлена
11),(
2
axxaxf
(см. рис.).
Следовательно, условия задачи эквивалентны системе
0),1(
0),1(
af
af
;
0111
0111
a
a
10
10
a
a
Ответ:
]10;10[
.
60
y=f(x,a)
-1 1
х
у
