Qiu X.G. (Ed.) High Temperature Superconductors

Подождите немного. Документ загружается.

392 High-temperature superconductors

43X

Rs is a measure of the rate of energy dissipation in the surface, and the surface

reactance Xs is a measure of the peak inductive energy stored in the surface.

Relating to complex conductivity, surface impedance can then be written as

[10.3]

In cases where the temperature is not too close to T

, where more superconducting

carriers are present, and

is ﬁnite but much smaller than

, an approximation

can be made. It then turns out that

[10.4]

with the frequency independent magnetic penetration depth

= (m /

)

1/2

where m is the mass of an electron and e is the charge on an electron.

From equation 10.4 important relations for surface resistance and reactance can

easily be derived:

[10.5]

and

Xs =

ωµ

[10.6]

It is well known that for a normal metal surface resistance increases with

1/2

whereas for a superconductor it increases with

. Knowledge of the frequency

dependence of surface resistance is especially important to evaluate the potential

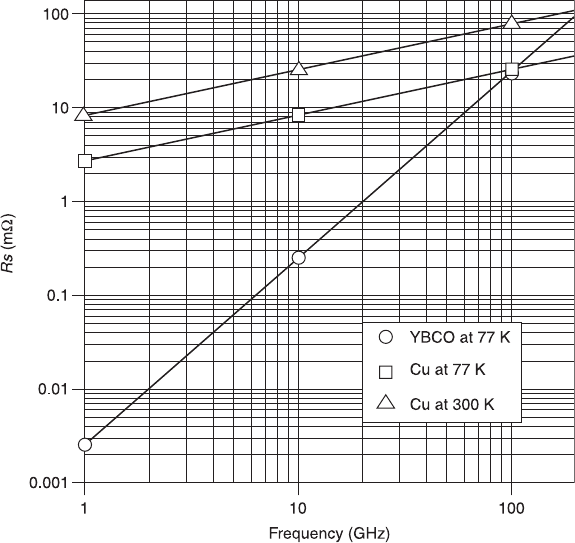
microwave applications of a superconductor. Hein (1999, p.93) showed a double-

logarithmic plot of surface resistance Rs versus frequency, depicting selected data

for granular and high quality epitaxial YBCO ﬁlms at 77 K. It can be seen from

Fig. 10.2 that YBCO displays a lower surface resistance than Cu, up to about

100 GHz, and that the overall trend resembles that of the conventional

superconductor Nb

Sn ﬁlms at 9 K. It can thus be concluded that the two-ﬂuid

formalism is capable of describing all measured data over 3 decades in frequency.

10.2.2 The non-linear microwave properties of

superconductors

Non-linearity is an important phenomenon in nature, which has profound signiﬁcance

for modern technology. Research into nonlinear microwave properties has revealed

a number of nonlinear phenomena, such as RF-vortex nucleation, annihilation and

motion, etc., which will bring new understanding of fundamental sciences. The

dynamics of various types of vortices behave in unique ways because the penetration

of the microwave current into the superconductor is quite different to that of d.c.

current. However, in this chapter we will concentrate our discussions on the effect of



Microwave ﬁlters using high-temperature superconductors 393

43X

the non-linearity of HTS materials on microwave devices, mainly in terms of the

substantial restriction of their power handling ability. The superior microwave

properties of HTS materials are only realized when the current density everywhere

within an HTS circuit is less than the critical value. If the power level of an HTS

microwave circuit is increased, the current density in the HTS material increases

accordingly. When the current density exceeds the critical value, the surface resistance

of the HTS material increases sharply, causing excessive loss in the circuit, and

eventually the performance collapses due to the transition into the non-superconducting

state. The nonlinear effects make the situation even worse. The non-optimized power

handling of HTS thin ﬁlms causes the performance of potentially linear devices to

deteriorate greatly (e.g., ﬁlters, delay lines) and limits optimization of the properties

of nonlinear devices (e.g., switches, power limiters). The power handling of HTS

devices is likely to be restricted by extrinsic sources, such as growth defects and

impurities within the ﬁlms, but precisely what type of defects and impurities

contribute to the nonlinear behaviour remains unclear for the time being. This is why

10.2 Frequency dependence of surface resistance Rs of high

temperature superconductor YBCO at 77 K (lowest line with symbol )

compared with normal metal Cu at 300 K (upper line with symbol △)

and 77 K (lower line with symbol ).



394 High-temperature superconductors

43X

nearly all modern HTS ﬁlter applications are positioned in the receiver (very low

power) side. However, the demand for HTS ﬁlters with higher power handling

ability, is increasing all the time (e.g., for applications of the electromagnetic

compatibility of the microwave transmitter). Therefore the study of the non-linear

microwave properties of superconductors, especially the HTS thin ﬁlms, has drawn

great attention from both scientists and engineers, and is one of the hot topics of

current research. The nonlinear microwave properties of HTS thin ﬁlms have most

commonly been studied by investigating the power dependence of the surface

impedance of un-patterned or patterned ﬁlms with coplanar, microstrip or stripline

arrangements. These studies can be carried out in the frequency domain or in the time

domain, where the dynamic response of the test objects to excitation pulses of

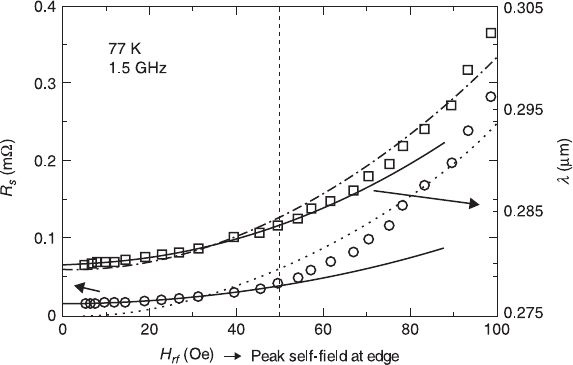
variable amplitude and duration can be investigated. Figure 10.3 shows a

representative example of the microwave magnetic ﬁeld H

dependence of R

and

. The low ﬁeld quadratic behaviour is usually attributed to the Ginzburg-Landau

depairing mechanism, in which Cooper pairs are broken by being accelerated beyond

the critical velocity in the microwave electric ﬁeld. The subsequent faster increase

(~H

) is usually dominated by hysteretic vortex penetration into the superconducting

grains (Nguyen et al., 1995). In this special case, the trends of the ﬁeld dependencies

of R

) and X

) are correlated. However, there is a wide variety of different

10.3 Typical power dependence of an epitaxial YBa

ﬁlm

measured with the help of the stripline resonator at f = 1.5 GHz and

77.4 K. The vertical dashed line at 50 Oe marks the approximate place

where R

and

deviated noticeably from a quadratic dependence on

. The solid lines are the best quadratic ﬁts to the low ﬁeld region

(< 50 Oe), the dashed lines are the best general quadratic ﬁts to the

entire ﬁeld range to demonstrate the nonquadratic behaviour of R

and

, see Nguyen et al. (1995).



Microwave ﬁlters using high-temperature superconductors 395

43X

power dependencies of R

) and X

) and, for most cases, the function behaviour

of R

) and X

) are not correlated. It might be argued that the loss of correlation

could result from the ﬁlms being made from different substrates, growth techniques

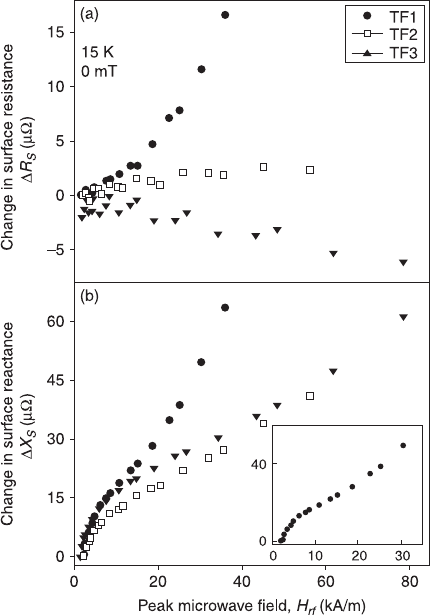
or/and heat treatments. An interesting result from Kharel et al. (1999) may give us a

clue as to how to clarify some of the confusing results mentioned above. They

showed three epitaxial co-evaporated YBCO ﬁlms on MgO substrates at different

temperatures, which demonstrated a great variety of behaviours, including decreasing,

independent and increasing functions of R

), despite the function form of X

)

being very similar for all the three ﬁlms (Fig. 10.4). From Equations 10.5 and 10.6 it

can be seen that R

∝

∝ n

, where

is the quasiparticle scattering time, and X

∝

∝ √n

. Since X

) does not vary from ﬁlm to ﬁlm, this strongly suggests that

there should be no profound changes in n

from sample to sample, and hence no such

10.4 The change in R

and X

for three epitaxial YBa

ﬁlms

on MgO substrates as a function of peak microwave ﬁeld H

dependencies. The measurements are made by using the coplanar

resonator technique at 8 GHz and 15 K. The inset shows data for

sample TF1 on an expanded scale, see Kharel et al. (1999).



396 High-temperature superconductors

43X

change in n

(since the total number of electrons is a constant). Therefore the

remarkable change of R

) most likely originates from the power-dependent

quiasiparticle conductivity

or, more precisely, from the power-dependent

, the

enhanced quasiparticle scattering due to defects and impurities. Those extrinsic

mechanisms probably co-exist with intrinsic ones (such as Ginzburg-Landau

depairing) and, acting together, lead to the uncorrelated behaviour.

Apart from the direct measurement of nonlinearity by studying the microwave

power (H

) dependence of surface impedance, harmonic generation (HG) and

intermodulation distortion products (IMD), measurements provide a more sensitive

probe of nonlinearity at extremely low power levels, where the device response

otherwise appears linear. According to the classical theory of IMD in nonlinear

systems, with the impedance being proportional to H

, IMD products generally

scale with the third power of the input power. This is usually referred to as 3:1

scaling. In IMD measurements, two microwave signals at frequencies f

and f

with a frequency separation of ∆

f being much less than f

or f

, are placed

symmetrically around the resonant frequency. The two microwave signals are

combined using a power combiner and passed through a variable attenuator to the

resonator loaded with ﬁlm. These nonlinear effects are often expressed by a single

parameter called the ‘third order intercept’, TOI, which is the intercept point of the

two input-output power lines for the fundamental and the third harmonic in a log-

log scale. The typical 3:1 behaviour of a three-pole YBCO band-pass ﬁlter with a

mid-band frequency of 9.5 GHz is demonstrated by Yoshitake and Tahara (1995),

where the upper line is the fundamental mode and the lower two lines are the third-

order distortion products, measured at 55 and 77 K, respectively. However

deviations from 3:1 are often reported from the literature. After considering a great

variety of power dependencies of Zs (H

), Velichko et al. (2005) found that, from

a theoretical point of view, the lower power slope must always be 3:1, independently

of the functional form of Zs(H

). But, at intermediate powers, IMD slopes may

indeed vary signiﬁcantly and can often be less than three. Therefore, Velichko

suggested that the deviation from the 3:1 scaling frequently observed in IMD

measurements of HTS ﬁlms has a purely technical origin, and proposed that the

spectral characteristics of microwave sources do not always allow the researchers

to use low enough powers to observe the 3:1 scaling. Instead, the measurements

are often possible only above a certain microwave power (set by the resolution of

the detection system), in which the slope is lower than 3:1.

10.3 Superconducting transmission lines and related

passive devices

10.3.1 Superconducting transmission lines

In microwave circuits, a transmission line is the material medium (or structure)

that forms all or part of a path for directing the transmission of electromagnetic



Microwave ﬁlters using high-temperature superconductors 397

43X

waves from one place to another. It not only serves as an interconnection between

the components in the circuits, but also often forms the basic element of

components and devices. It is indeed the foundation of microwave circuits, and

most microwave theories have originated directly or indirectly from transmission

theory, something which is also true for superconducting devices.

The most important effect of superconducting transmission lines is their very

low loss. A superconducting transmission line is dispersionless, provided the

wave propagated is in a TEM mode. This is due to the fact that the penetration

depth does not vary with frequency, a contrast with normal conductors, where

skin depth is a function of frequency.

The realistic transmission line model represents the transmission line as an inﬁnite

series of two-port elementary components, each representing an inﬁnitesimally short

segment of the transmission line with distributed resistance R, inductance L, and

capacitance C. Transmission lines which are commonly used include wires, coaxial

cables, dielectric slabs, optical ﬁbres, electric power lines, waveguides, and planar

transmission lines, etc. Considering that most superconducting ﬁlters are based on

superconducting ﬁlms, in this chapter we will concentrate on the planar transmission

lines, i.e., microstrip, coplanar, and stripline.

Microstrip is a widely used type of microwave transmission line, which consists

of a conducting strip (with a width w and a thickness t) separated from a ground

plane by a dielectric layer known as the substrate (with a dielectric constant

and a thickness d). The general structure of a microstrip is shown schematically in

Fig. 10.5(a). The ﬁelds in the microstrip extend within two media: air above and

dielectric below. In general, the dielectric constant of the substrate will be greater

than that of the air, so the wave is travelling in an inhomogeneous medium. In

consequence, the propagation velocity is somewhere between the speed of

microwaves in the substrate and the speed of microwaves in air. This behaviour is

commonly described by stating the effective dielectric constant (or effective

relative permittivity) of the microstrip, this being the dielectric constant of an

equivalent homogeneous medium. Due to its inhomogeneous nature, the

microstrip line will not support a pure TEM wave; both the E and H ﬁelds will

have longitudinal components. However, the longitudinal components are small,

so the dominant mode is referred to as quasi-TEM. The ﬁeld propagation

velocities will depend not only on the properties of the material, but also on the

physical dimensions of the microstrip. Compared to other transmission lines, such

as traditional waveguide technology, the advantage of a microstrip is that it is

much less expensive, as well as being far lighter and more compact. On the other

hand, the disadvantages of a microstrip compared to a waveguide are its generally

lower power handling capacity, and higher losses, of which the latter can be

greatly improved through the use of superconducting materials.

A coplanar line is formed from a conductor separated from a pair of ground

planes, all on the same plane, at the top of a dielectric medium (Fig. 10.5(b)). In

an ideal case, the thickness of the dielectric is inﬁnite; in practice, it should be



398 High-temperature superconductors

43X

thick enough so that EM ﬁelds die out before they leave the substrate. The

advantages of a coplanar line are that active devices can be mounted on top of the

circuit, as on a microstrip. More importantly, it can provide an extremely high

frequency response (100 GHz or more) since connecting to a coplanar line does

not entail any parasitic discontinuities in the ground plane. This means that only

single-side superconducting ﬁlm is required for a superconducting coplanar line,

which greatly reduces the difﬁculties in ﬁlm making since double-sided ﬁlms

need special technology, especially for those newly discovered superconductors.

One of the disadvantages of the coplanar line is the imbalance in its ground planes,

although they are connected together at some points in the circuit. The potential

of the ground planes can become different on each side, which may produce

unwanted modes and interference. The problem can be solved to some extent by

connecting the two ground planes somewhere in the circuit with a ‘ﬂying wire’

(air bridge) over the conducting plane. However, it will create other problems,

such as greater complexity.

A standard stripline uses a ﬂat strip of metal, which is sandwiched between two

parallel ground planes (Fig. 10.5(c)). The width of the strip, the thickness of the

substrate (the insulating material between the two ground plans) and the relative

permittivity of the substrate determine the characteristic impedance of the

transmission line. The advantage of the stripline is that radiation losses are

eliminated and a pure TEM mode can be propagated within it. The disadvantage

of the stripline is the difﬁculty in constructing it, especially in superconducting

ﬁlms. It requires two pieces of superconducting ﬁlms, both double-sided, or one

single- plus one double-sided ﬁlm. The air gap, though extremely small, will

cause perturbations in impedance as well as making it very difﬁcult to form

contacts with external circuits. Besides, if two pieces of double-sided ﬁlms are

used, the need for precise aiming between the very ﬁne patterns of two ﬁlms

creates another problem.

10.3.2 Application of transmission lines 1:

superconducting delay line

A delay line consists of a long transmission line, which is used to delay incoming

signals for a given amount of time, while minimizing the distortion caused by

10.5 Cross-section geometries of microstrip (a), coplanar line (b), and

stripline (c).



Microwave ﬁlters using high-temperature superconductors 399

43X

crosstalk, dispersion and loss. Conventional delay lines, such as coaxial cables

and printed circuit delay lines, present the problems of large volume and

unacceptable insertion loss. Superconducting delay lines with extremely small

losses and compact sizes offer a promising solution for these problems.

All of the three types of superconducting transmission lines mentioned above

can be used for making delay lines. However, the advantages of coplanar lines are

distinctive. First, the ground planes in between the signal line provide a shield,

which reduces the crosstalk. Secondly, the line width of the signal line is quite

ﬂexible since the impedance of the coplanar line is mainly determined by the ratio

between the signal line width and the gap width. The disadvantage is that the

unwanted odd mode can be excited by turnings, curvatures, or any asymmetry

with respect to the signal line, which can be resolved by bonding crossover ‘ﬂying

wires’ (air bridges) between the ground planes over the top of the signal line.

Stripline is the only planar transmission line without modal dispersion. It has a

longer delay per unit length, since the signal propagation velocity is slower than

that of the other two lines. It also has less cross talk than the microstrip line due to

the existence of the top plane. An excellent example of the application of striplines

can be found in the work reported by Lyons et al. (1996), where the delay line was

used for a chirp-response tapped ﬁlter. They used a pair of YBCO striplines to

form a double spiral conﬁguration and the chirp function was achieved by a series

/4 backward-wave couplers to realize the requested frequency dependent

delay for different frequency components in the signal. This chirp ﬁlter was

installed in a 3 GHz band width spectral analysis receiver.

10.3.3 Application of transmission lines 2:

superconducting resonator

A microwave resonator is a simple structure, which can be made of cavity or

transmission line, and is able to contain at least one oscillating electromagnetic

ﬁeld. If an oscillating ﬁeld is set up within a resonator, it will gradually decay

because of losses. By using superconductors, the losses can be greatly reduced

and high Q-values can then be achieved. Resonators are the most fundamental

building blocks in the majority of microwave circuits. By coupling a number of

resonators together, a microwave ﬁlter can be constructed. A high Q-resonator

forms the main feedback element in a microwave oscillator. The quality factor for

a resonator is deﬁned by

[10.7]

where w is the energy stored in the resonator, and p is the dissipated energy per

period in the resonator.

Losses in a resonator occur due to a number of mechanisms. The most important

are usually the losses associated with conduction currents in the conducting layer



400 High-temperature superconductors

43X

of the cavity or transmission line, the ﬁnite loss tangent of the dielectric substrate,

and radiation loss from the open aperture. The total quality factor can be found by

adding these losses together, resulting in

[10.8]

where Q

, Q

, and Q

are the conductor, dielectric and radiation quality factors,

respectively. For conventional cavity or transmission line resonators at microwave

frequency, Q

usually dominates. This is why a superconductor can greatly

increase the Q-value of the resonators.

For superconducting resonators, the resonant frequency and the Q-values (both

loaded Q

and unloaded Q

values) are temperature dependent, and the variation

is remarkable when close to T

, as shown in Fig. 10.6 (Li et al., 2002). It is

10.6 Temperature dependence of resonate frequency (a) and Q-values

(b) of superconducting resonator, see Li et al. (2002).



Microwave ﬁlters using high-temperature superconductors 401

43X

therefore preferable to operate at a temperature below 80% of T

, where a more

stable resonant frequency and a high enough Q-value can be achieved.

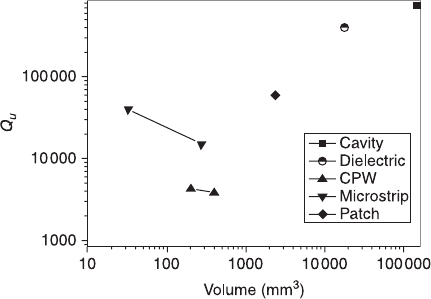
Aside from the Q-value, size is also important in an HTS resonator, not only in

terms of the commercial consideration of reducing the cost, but also because the

HTS ﬁlters need to work at low temperatures and their large size will increase the

burden on the cryo-cooler. However, high quality factor and minimal size are

often a contradictory pair because a reduction in size always results in a reduction

in the stored energy, and hence the Q-values. The quality factors and volumes of

various kinds of HTS resonators are shown in Fig. 10.7 in dual-log coordinate at

frequency around 5 GHz. All the data come from literature published over the last

decades. Here, the volume of the planar resonators is calculated by assuming it

has a height of 8 mm.

HTS cavity resonators are usually designed to resonate in the TE

011

mode. In

this mode, the current ﬂow is circumferential, so there is no current ﬂow across

the join of the side wall and the end plates. Although such structures have very

high Q-values, their volume becomes prohibitively large at low frequencies. HTS

dielectric resonators usually consist of a dielectric rod of single crystal material,

which is sandwiched between two planar HTS ﬁlms. They can have very high

Q-values (if very large area high quality superconducting ﬁlms are applied), but

are smaller than unloaded resonant cavities. Due to their large volume and

difﬁculty in realizing cross couplings, HTS cavity resonators and HTS dielectric

resonators are often used to construct low-phase noise oscillators and, in the case

of the dielectric ones, to measure the surface resistance of HTS thin ﬁlms. They

are seldom used in HTS ﬁlters. Patch resonators, which are two dimensional

resonators, are of interest in the design of high power handling HTS ﬁlters. An

associated advantage of these resonators is their lower conductor losses compared

with one dimensional line resonators. However, patch resonators tend to have

stronger radiation, so they are not suitable for designing narrow band ﬁlters. The

10.7 The quality factor vs. volume of different kinds of HTS resonators.

