Реферат - Комплексные числа и их свойства
Подождите немного. Документ загружается.

.
22
2222
aba
b
b
i
aba
bia
Пример 1. Вычислить:
i
Здесь z=i=0+1
.1,0.., baетi
По теореме получаем:
.
2
1
2
1
2
010
1
1
2
010
2222
iii
Пример 2. Извлечём, например, квадратный корень из действительного
отрицательного числа (-a
2
) и покажем, что
2
а
= +ai или
2
а
= -ai. В
частности,
1
= +-i.
Полагая
2
а
= х + yi, имеем (x + yi)
2
= -a
2
или (x
2
– y
2
) + 2xyi = -a
2
. Отсюда
получаем систему двух уравнений
;02
,
222
xy
ayx
решив которую, найдём, что x = 0, y = +-a
(случай у = 0 невозможен, так как при этом х
2
= -а
2
, что неверно для
действительных чисел). Поэтому
2
а
= +-ai.
Доказано, что корень
n
z
всегда существует и имеет ровно n различных
значений, если z≠0. Очевидно,
n
0
= 0.
11

4. Основная теорема алгебры.
Комплексные числа обладают алгебраической замкнутостью – всякое
алгебраическое уравнение с комплексными коэффициентами имеет корни.
Например, уравнение х
2
– 4х + 13 = 0 имеет отрицательный дискриминант (D =
=16-52=-36 < 0), но корни этого уравнения будут х
1
= 2-3i и х
2
= 2+3i, т.е.
квадратное уравнение из множества комплексных чисел имеет два
комплексных числа корнями уравнения.
А. Жирар и Р. Декарт сформулировали основную теорему алгебры – всякое
алгебраическое уравнение имеет столько корней, какова его степень. А доказал
эту теорему немецкий математик К. Гаусс.
Карл – Фридрих Гаусс (1777 – 1855). Знаменитый немецкий
математик. Гаусс – человек с универсальными
математическими способностями; им затрагивались почти
все главные отрасли чистой и прикладной математики.
Гаусс создал множество математических трудов, среди
которых: «О протяжении эллипсоидов», «Мемуары по
теории биквадратичных вычетов, в которых впервые
введено в теорию чисел понятие о целых комплексных
числах вида а + bi» и многие другие.
12
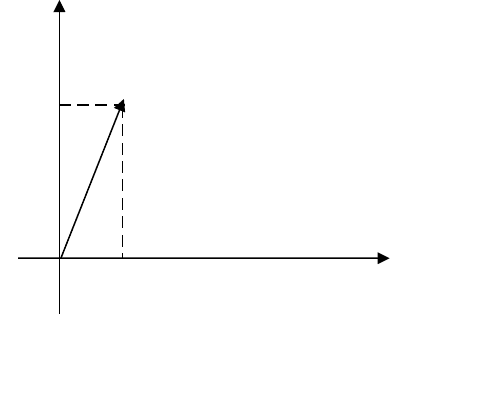
5.Геометрическое изображение комплексных чисел.
Комплексным числам соответствуют простые геометрические образы на
двумерной плоскости. В этом случае ось x называют действительной осью, ось
y– мнимой осью, а саму плоскость (xy)– плоскостью комплексных чисел, или z-
плоскостью. Комплексное число изображают либо точкой с координатами (a,
b), либо вектором с началом в центре координат (0, 0) и концом в точке с
координатами (a, b) (см. Рисунок).
Мнимая ось
Lm
Действительная ось
Re
0
z = a+bi
13
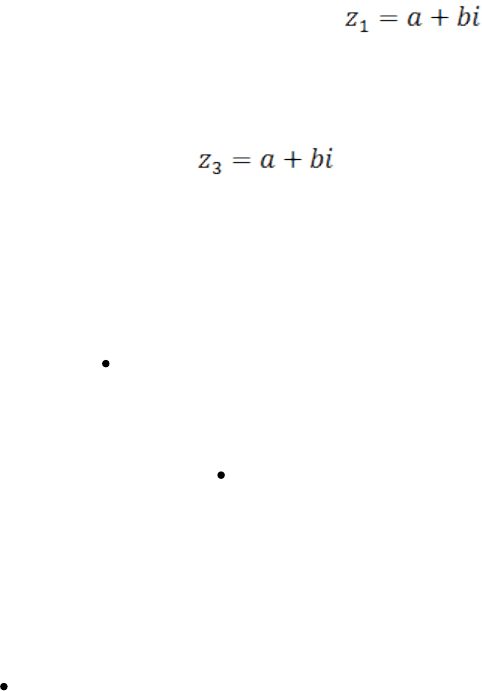
6.Комплексные числа и координатная плоскость.
При переходе к геометрической модели множества С комплексных чисел
требуется, как минимум, ещё одно измерение: ведь все точки прямой уже
«заняты» действительными числами. Оказывается, геометрической моделью
множества C является координатная плоскость. Каждому комплексному числу
можно естественным образом поставить в соответствие точку координатной
плоскости. Тогда любому комплексному числу соответствует единственная
точка на координатной плоскости, и наоборот, каждая точка плоскости
является «изображением» единственного комплексного числа.
В случае с комплексными числами, в соответствие с числовой прямой,
отождествление с точками координатной плоскости. Например, фраза: «число
z
1
лежит в первой координатной четверти» - просто означает, что и
действительная и мнимая части комплексного числа
положительны. Слова «z2 лежит на оси ординат» являются переводом на
геометрический язык того факта, что число z
2
чисто мнимое, а «…комплексное
число z
3
расположены выше биссектрисы 1 и 3 координатных четвертей…» –
показывают, что мы имеем дело с комплексным число , у которого
мнимая часть больше действительной части.
Иногда приведенные правила для сложения, вычитания комплексных чисел и
умножения комплексных чисел на действительные числам объединяют таким
образом: во множество комплексных чисел операции сложения, вычитания и
умножения вычитания и умножения на действительные числа производятся
покоординатно. Подчеркнем что сама эта формулировка предполагает
операции уже не с самими комплексными числами, а с их геометрическими,
векторными представлениями.
у
х
0
Z
3
Z
1
Z
2
y=x
14
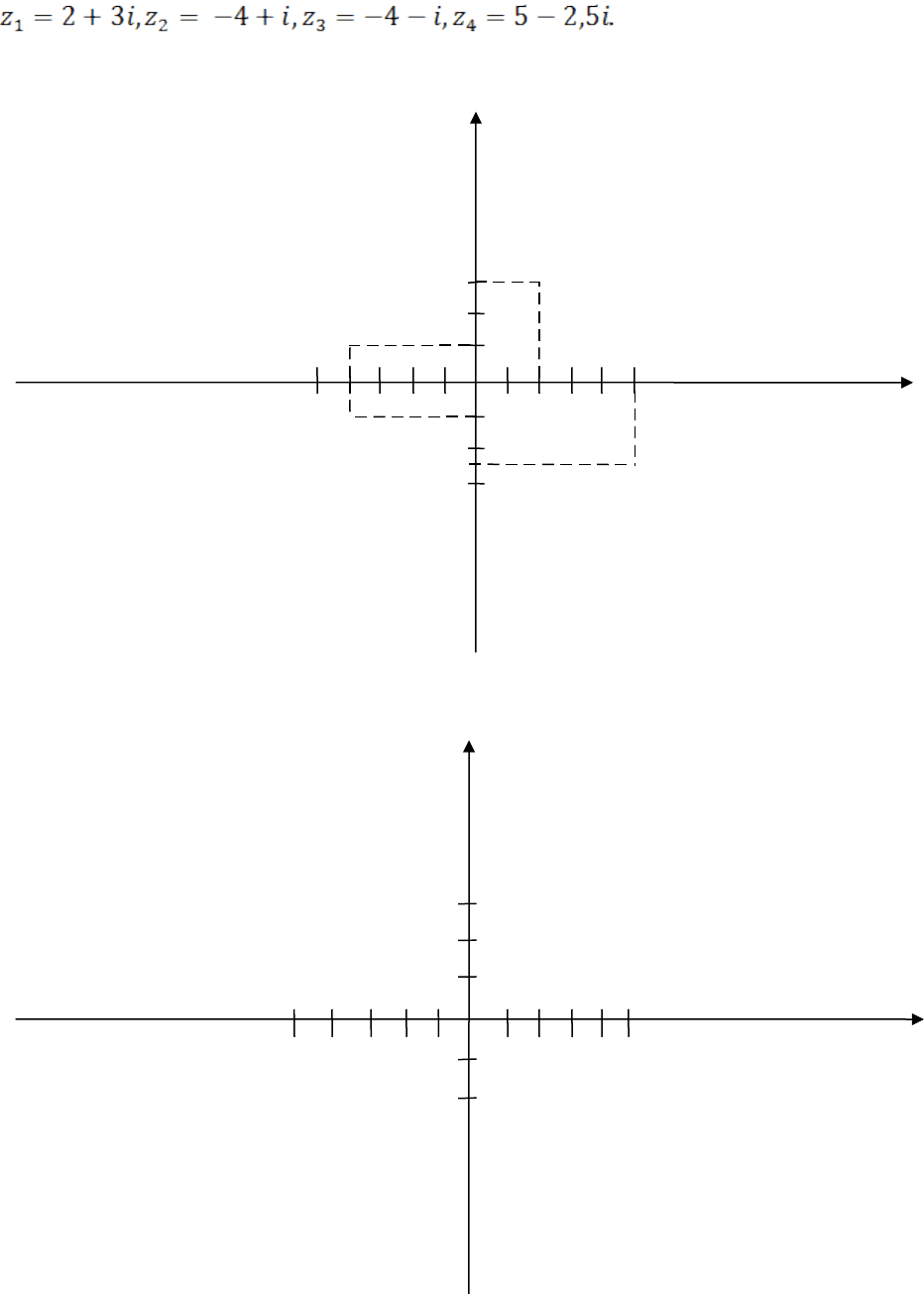
На координатной плоскости отмечены комплексные числа:
На координатной плоскости отмечены некоторые действительные и чисто
мнимые числа: 0, 5, -3,5, i, -2i.
y
x0
3
5
Z
1
Z
4
Z
3
Z
2
x
0
5
i
-2i
-3,5
y
15
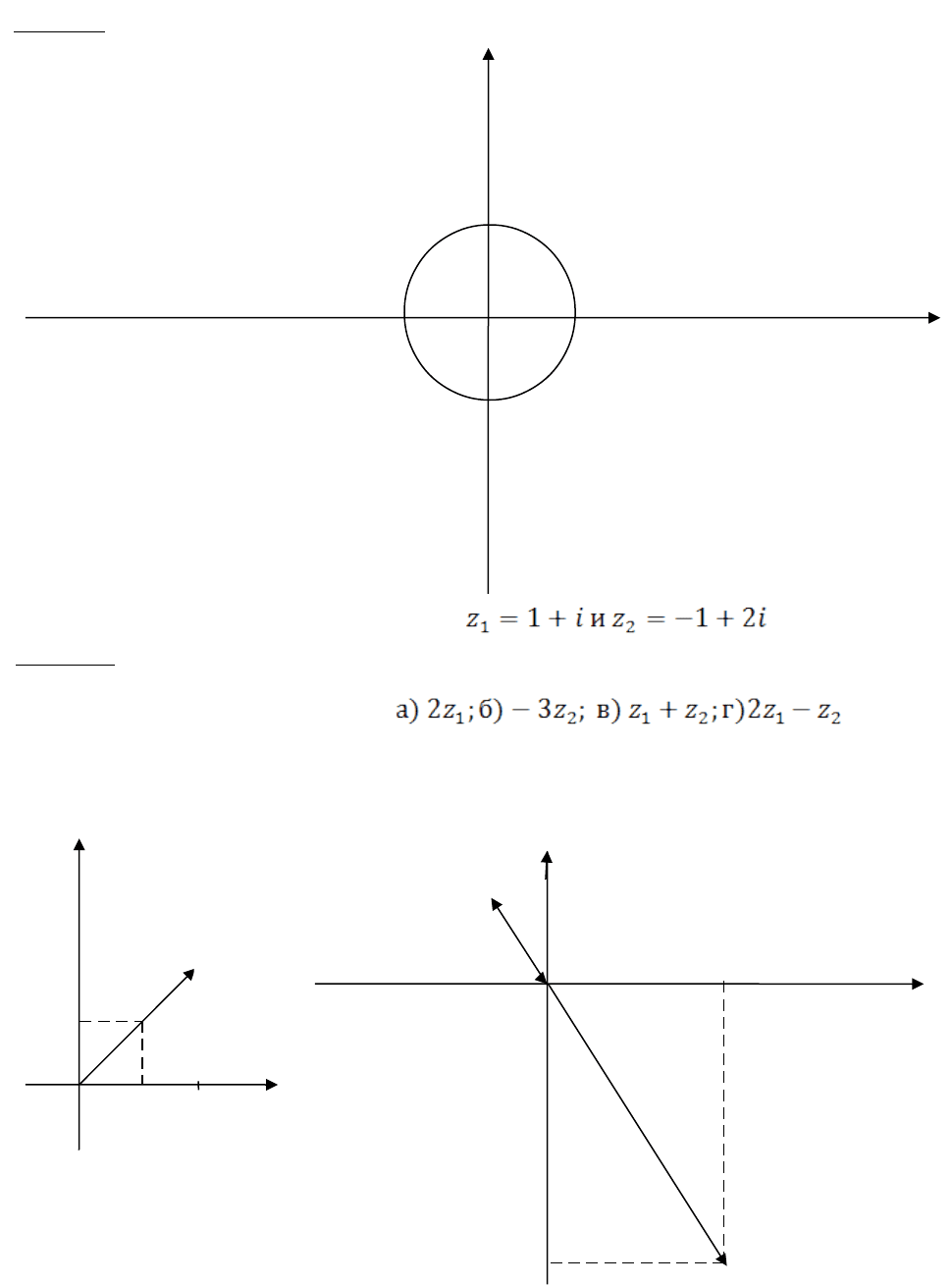
Пример. Для комплексных чисел изобразить на
координатной плоскости числа: .
Решение:
y
x
0
3
3
y
x
а)
1
1
z
1
2z
1
2
-3Z
2
z
2
0
y
x
б)
-3z
1
-6
3
16
Пример. Изобразить на
координатной плоскости
множество всех комплексных
чисел, у которых сумма квадратов
действительной и мнимой частей
равна 9.
Нас интересуют
комплексные числа
z = x + yi, у которых
x
2
+y
2
= 9. Это окружность
радиусом 3 с центром в
начале координат
Иногда приведенные правила для сложения, вычитания комплексных чисел и
умножения комплексных чисел на действительные числа объединяют таким
образом: во множестве комплексных чисел операции сложения, вычитания и
умножения на действительные числа производятся покоординатно.
Подчеркнем, что сама формулировка предполагает операции уже не с самими
комплексными числами, а с их геометрическими, векторными представлениям.
7.Модуль комплексного числа.
Модулем комплексного числа называют число .
Обозначение: .
Пример найти модуль комплексного числа:
i
i
г
iiв
i
б
iа
1
)
)1()
10
)
2021)
Решение.
29841400441)20(212021)
22
ia
y
0
x
Z
1
Z
2
Z
1
+ Z
2
в)
-1
1
y
x
0
Z
2
-Z
2
2Z
1
Z
1
2Z
1
– Z
2
г)
2
2
17
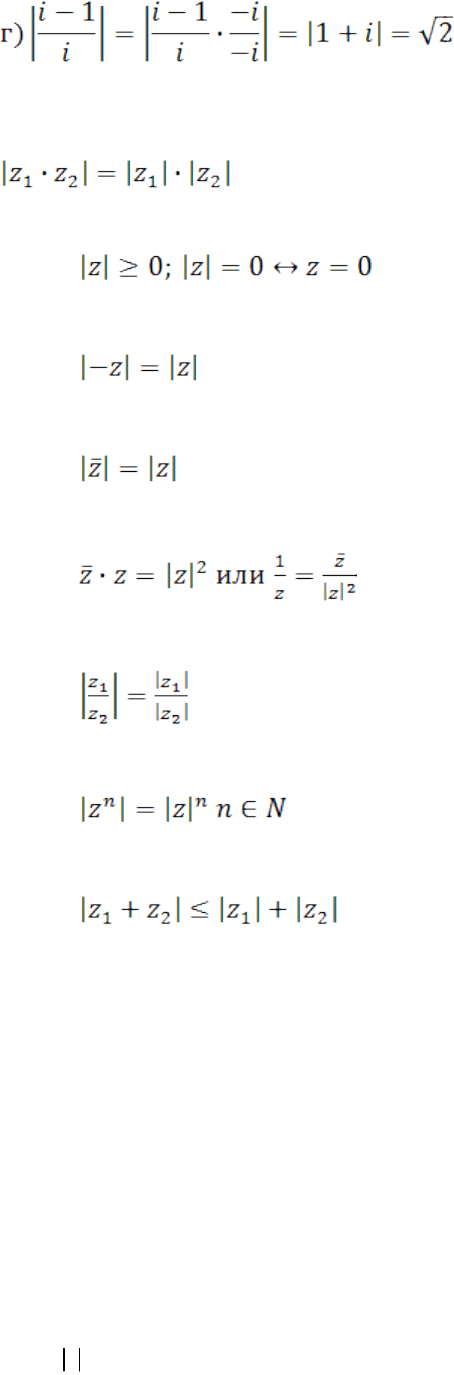
Теорема. Модуль произведения двух комплексных чисел равен произведению
модулей этих чисел:
Свойства модуля:
1)
2)
3)
4)
5)
6)
7)
aДлина вектора, изображающего комплексное число, называется модулем этого
комплексного числа. Модуль всякого комплексного числа, не равного нулю,
есть положительное число. Модуль комплексного числа a + bi обозначается
| a + bi |, а также буквой r.
r = | a + bi | = a
2
+ b
2
aМодуль действительного числа совпадает с его абсолютным значением.
Сопряжённые комплексные числа a + bi u a – bi имеют один и тот же модуль.
8.Аргумент комплексного числа
Аргументом отличного от нуля комплексного числа z называют
действительное число α такое, что:
sincos)
;;)
izzб
а
Обозначение: arg z
18
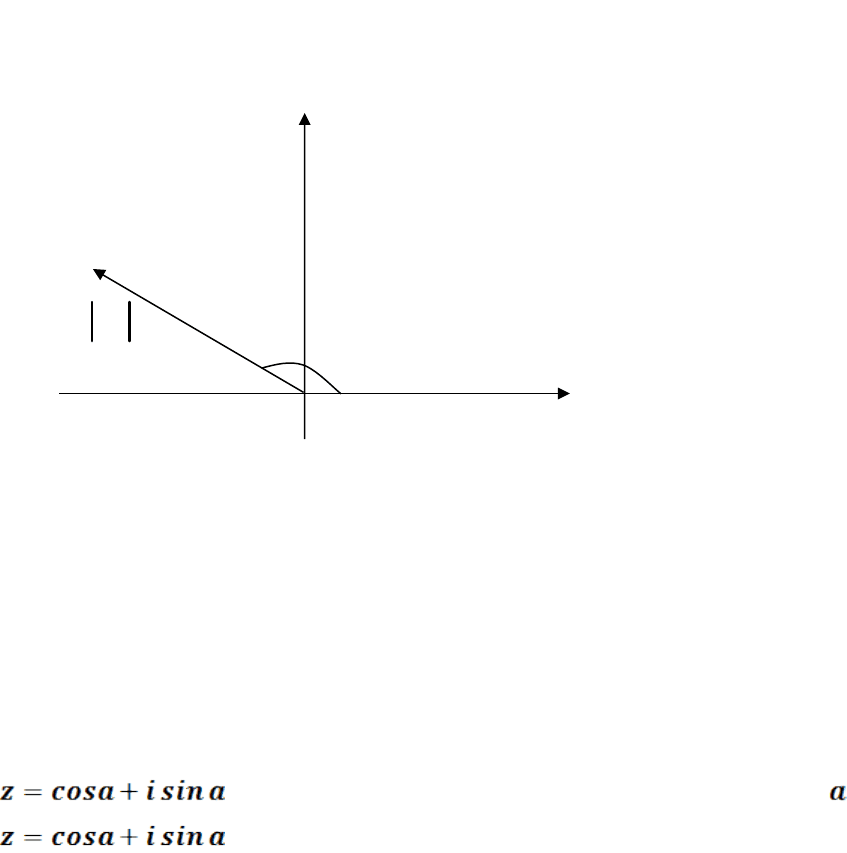
Геометрически аргумент комплексного числа z можно истолковать так: это
угол, заключенный в пределах
;
, который вектор z образует с
положительным направлением оси абсцисс.
9.Перевод z = a + bi из алгебраической формы в тригонометрическую.
Теорема. Если комплексное число z лежит на числовой окружности, то
для некоторого действительного числа ; если
, то z лежит на числовой окружности.
О
z
z
y
x
arg z
19
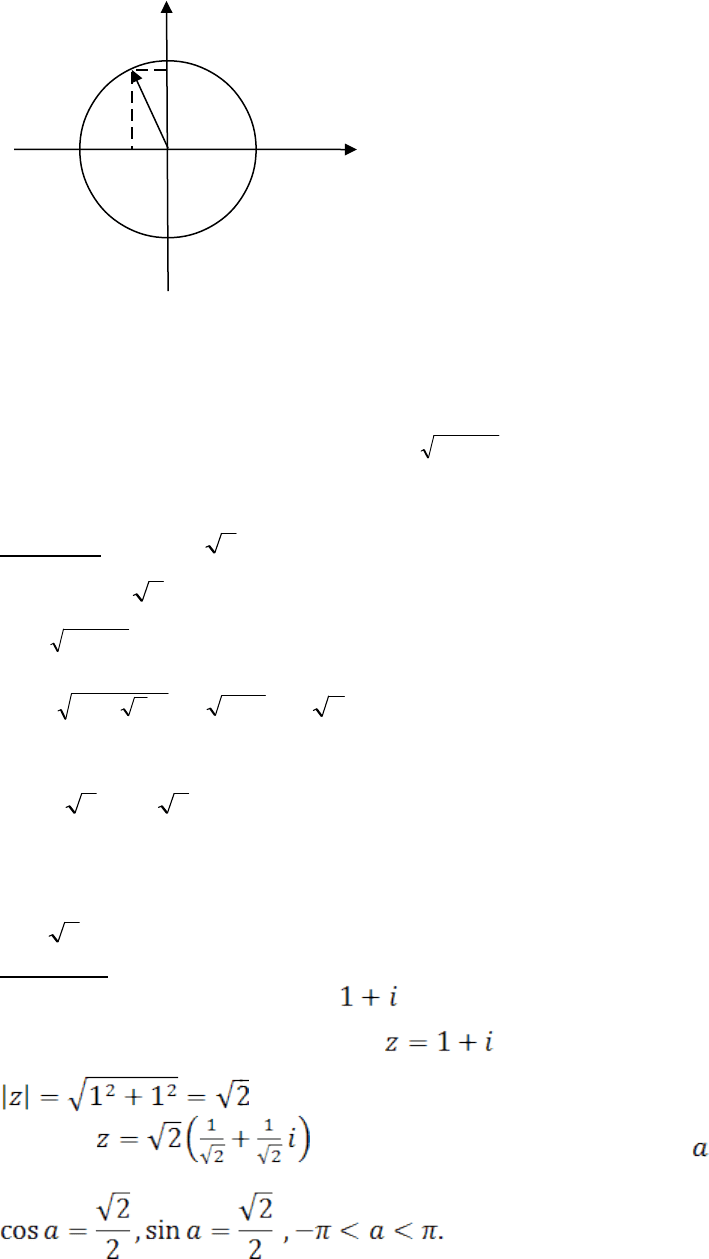
1. Введём обозначение r = |z | =
22
bа
2. tgφ = b/a. Отсюда мы можем найти сам угол φ
3. z = r(cosφ + i sinφ). Перевод очевиден.
Пример. z = 1 +
3
.
i
a = 1 b =
3
|z| =
22
bа
|z| =
22
)3(1
=
31
=
4
= 2;
tgφ = b/a;
tgφ =
3
/1 =
3
; φ = 60
0
;
z = |z|(cosφ + i sinφ);
z = 2(cos60
0
+ i sin60
0
);
1 +
3
= 2(cos60
0
+ i sin60
0
).
Пример. Записать данное комплексное число в стандартной
тригонометрической форме
Решение. Найдём модуль числа . Получим:
Значит, . Осталось вычислить аргумент :
x
y
1
-1
z
0
cos α
sin α
20
