Русаков В.С. и др. Механика. Методика решения задач

Глава 7. Законы сохранения момента импульса и механической энергии

261

Решение

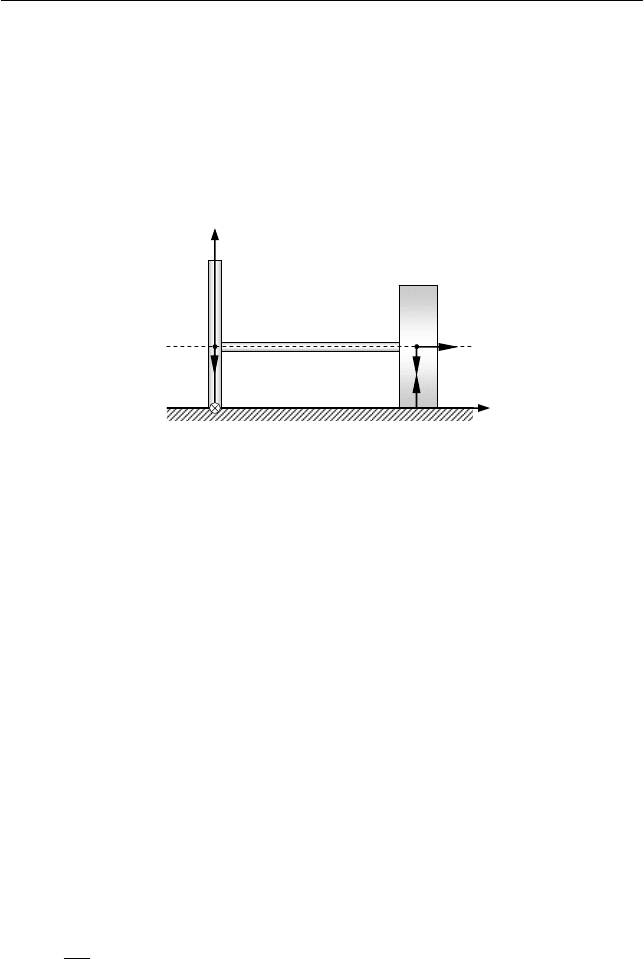
I. Выберем оси декартовой системы координат так, как пока-

зано на рис. 7.18. Каток участвует в двух движениях – вращении

вокруг вертикальной оси Z с угловой скоростью

ω

и вокруг собст-

венной геометрической оси AA' с угловой скоростью

ω

1

. Направ-

ления угловых скоростей показаны на рис. 7.18. Неподвижной ос-

тается точка крепления катка к вертикальной оси – точка C.

На каток действуют сила тяжести

mg, сила реакции опоры N

и сила реакции со стороны вертикальной оси, приложенная в точке

С (не изображенная на рис. 7.18). Будем считать стержень, с помо-

щью которого каток крепится к вертикальной оси, невесомым. По

условию задачи цилиндрический каток движется без проскальзы-

вания, это означает, что толщина катка существенно меньше рас-

стояния

R от катка до вертикальной оси вращения. Трением каче-

ния, возникающим при неупругих деформациях, пренебрегаем. По

условию задачи требуется найти полную силу давления катка на

опорную плиту, которая в соответствии с третьим законом Ньюто-

на равна по модулю силе нормальной реакции опорной плиты

N,

действующей на каток.

II. Отличные от нуля моменты относительно точки C имеют

две силы – сила тяжести

mg

M и сила нормальной реакции со сто-

роны горизонтальной поверхности

N

M

. Запишем уравнение мо-

ментов для катка относительно точки C крепления катка к верти-

кальной оси:

mgN

t

MM

L

+=

d

.

(7.105)

Рис. 7.18

ω

R

X

Z

Y

N

mg

ω

1

C A A'

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

262

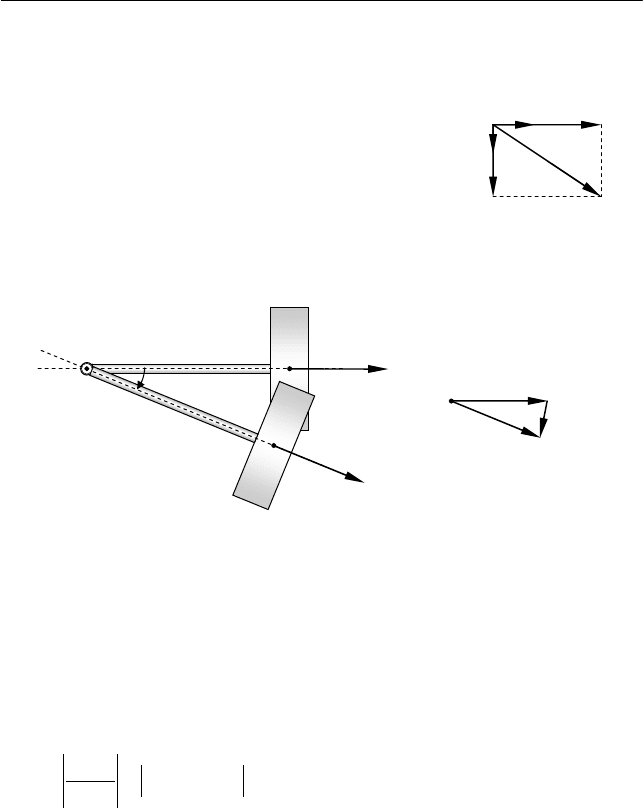
При качении катка по горизонтальной поверхности происхо-

дит постоянное изменение направления его оси, что определяет

изменение направления вектора момента им-

пульса. Горизонтальная составляющая мо-

мента импульса

XY

L (см. рис. 7.19) повора-

чивается вокруг оси Z (см. рис. 7.20), а вер-

тикальная составляющая

Z

L остается неиз-

менной:

XYZXY

dddd LLLL =+

=

. (7.106)

Моменты силы тяжести

mg

M и силы нормальной реакции

опорной плиты

N

M относительно точки C направлены в противо-

положных направлениях вдоль оси Y (см. рис. 7.18). Следователь-

но, для величины скорости изменения горизонтальной составляю-

щей момента импульса

XY

L с учетом (7.105) и (7.106) можно запи-

сать:

RmgRN

t

mgN

−=+= MM

L

d

XY

. (7.107)

Поскольку составляющая момента импульса

XY

L направлена

вдоль собственной геометрической оси катка AA', то в соответст-

вии с формулой (6.30) Главы 6:

10XY

ω

JL = . (7.108)

В соответствии с условием задачи качение происходит без

проскальзывания, следовательно, скорости точек катка, соприка-

сающихся с горизонтальной поверхностью, равны нулю. С другой

Рис. 7.19

ω

1

ω

L

z

L

xy

L

Рис. 7.20

L

xy

(t)

L

xy

(t+dt)

d

α

Z

L

xy

(t)

L

xy

(t+dt)

d

L

xy

Глава 7. Законы сохранения момента импульса и механической энергии

263

стороны, в силу принципа суперпозиции движений, скорость этих

точек складывается из скорости вращения вокруг вертикальной оси

и скорости вращения вокруг собственной оси катка. Следовательно

угловые скорости

ω

и

ω

1

связаны соотношением:

0

1

=

−

rR

ω

. (7.109)

Найдем величину скорости изменения горизонтальной со-

ставляющей момента импульса

XY

L . В соответствии с рис. 7.20.

можно записать:

ω

α

XY

XYXY

d

L

t

L

t

L

==

. (7.110)

В результате получена полная система уравнений (7.107) –

(7.110) для нахождения

N.

III. Решая систему уравнений (7.107) – (7.110) относительно

величины силы нормальной реакции опорной плиты, получаем:

()

mgNR

r

R

J

t

L

−==

2

0

XY

d

ω

, (7.111)

mg

r

J

N +=

2

0

ω

. (7.112)

В соответствии с третьим законом Ньютона искомая полная

сила давления катка на опорную плиту равна по модулю силе нор-

мальной реакции опорной плиты

N, действующей на каток (7.112).

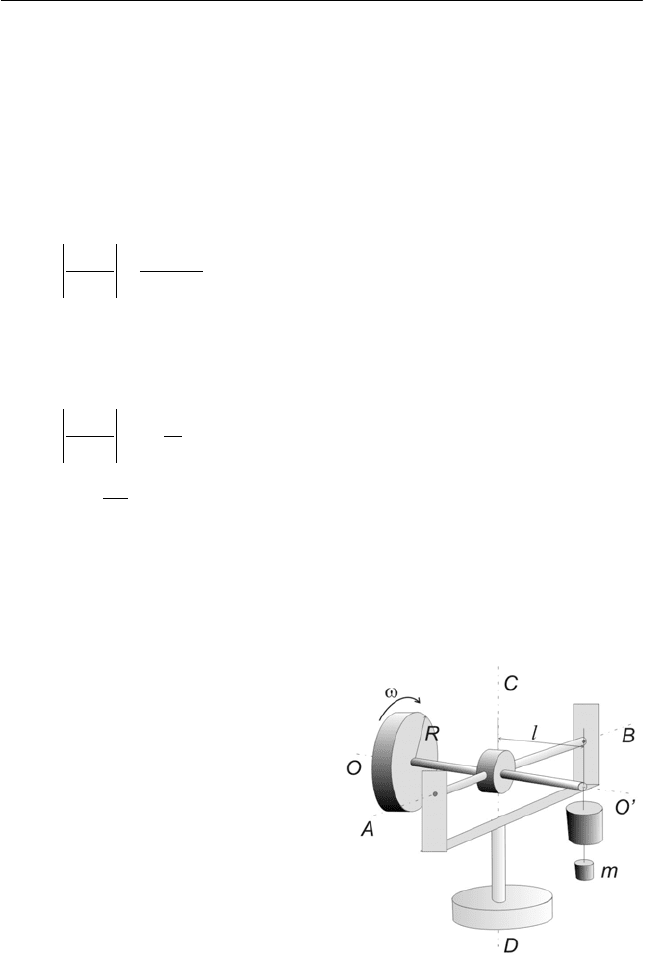
Задача 7.9

Гироскоп представляет со-

бой однородный диск радиусом

R = 5 см и массой m

0

, закреплен-

ный на невесомом горизонталь-

ном стержне, ориентированном

вдоль оси OO' (рис. 7.21). Гиро-

скоп может вращаться вокруг

осей OO' и CD. Диск гироскопа

уравновешен на другом конце оси

OO' телом с той же массой

m

0

.

Гироскоп раскрутили вокруг соб-

ственной оси OO' так, что он де-

лает

n = 50 об./с. Затем к телу

массой

m

0

подвесили еще одно

Рис. 7.21

m

0

,

m

0

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

264

тело массой 10/

0

mm = . Найти период вращения гироскопа вокруг

оси CD, если расстояние

l от оси CD до точки подвеса тела массой

m

0

(см. рис. 7.21) равно 10 см.

Решение

I. До подвешивания тела массой m гироскоп уравновешен,

следовательно сумма моментов силы тяжести, действующей на

диск гироскопа, и силы натяжения нити подвеса тела массой

m

0

относительно точки пересечения осей вращения OO' и CD гироско-

па равна нулю. В условии равновесия гироскоп не совершает пре-

цессии. После подвешивания тела массой

m увеличивается момент

силы натяжения нити подвеса, что приводит к изменению момента

импульса гироскопа. Поскольку момент импульса гироскопа зна-

чительно больше изменения момента силы натяжения нити подве-

са, то происходит медленное изменение направления момента им-

пульса гироскопа

L – прецессия оси гироскопа.

II. Запишем уравнение прецессии гироскопа (см. (7.23)) отно-

сительно точки пересечения его осей вращения OO' и CD (см.

рис. 7.18):

[]

ΩLM

=

, (7.113)

где

M − сумма моментов внешних сил, действующих на гироскоп,

Ω − угловая скорость прецессии.

Дополним это уравнение выражением (7.18) для момента им-

пульса гироскопа относительно его собственной оси OO':

ωL

0

J

=

. (7.114)

Здесь момент инерции гироскопа, представляющего собой одно-

родный диск, закрепленный на невесомом стержне, в соответствии

с формулой (6.44) в Главе 6 равен

2

0

Rm

J =

, (7.115)

а угловая скорость вращения гироскопа

ω

связана с числом его

оборотов

n вокруг собственной оси соотношением:

n

π

ω

2

=

. (7.116)

Подвешенные к стержню гироскопа тела массой

m

0

и m не

перемещаются вдоль вертикальной оси CD в процессе движения

гироскопа, поэтому в соответствии со вторым законом Ньютона

сила натяжения нити подвеса тел

F равна

()

gmmF +

=

0

. (7.117)

Глава 7. Законы сохранения момента импульса и механической энергии

265

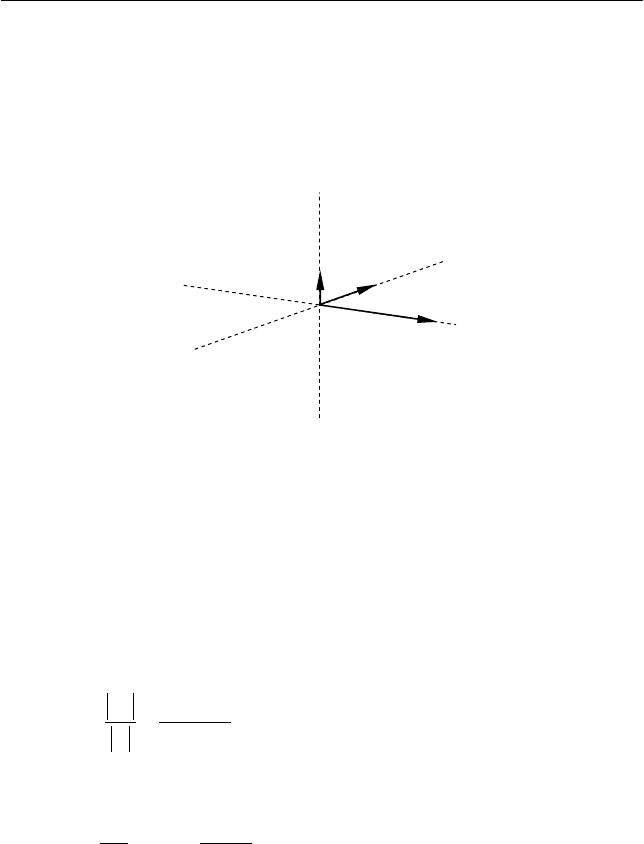
Сумма моментов силы тяжести, действующей на диск гиро-

скопа массой

m

0

, и силы натяжения нити подвеса тел массой m

0

и m

относительно точки пересечения осей вращения OO' и CD гироско-

па направлена вдоль оси AB (см. рис. 7.22) и равна по модулю

()

mglglmmglmM

=

++−

=

00

. (7.118)

Вследствие быстрого вращения гироскопа вокруг своей оси

его момент импульса будем считать направленным вдоль оси вра-

щения OO' (рис. 7.22). При этом угловая скорость прецессии

Ω в

соответствии с (7.113) направлена вдоль оси CD (рис. 7.22).

Подставляя (7.114) – (7.118) в (7.113) с учетом направления

векторов

M

, L и Ω , для модуля угловой скорости прецессии ги-

роскопа

Ω

получаем:

2

0

Rnm

mgl

π

Ω

==

L

M

. (7.119)

Искомый период вращения гироскопа вокруг оси CD в соот-

ветствии с (7.118) равен:

mgl

Rm

nT

2

0

2

π

Ω

π

== . (7.120)

Подставляя численные значения физических величин, задан-

ных в условии задачи, получим

c5,12

=

T .

A

B

O

O'

C

D

L

MΩ

Рис. 7.22

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

266

7.4. Задачи для самостоятельного решения

Задача 1

Диск, вращающийся с угловой скоростью

ω

1

вокруг верти-

кальной оси, проходящий через его центр масс, падает на другой

диск, вращающийся на гладкой горизонтальной поверхности с уг-

ловой скоростью

ω

2

вокруг той же оси (см. рис.). Моменты инер-

ции дисков относительно оси враще-

ния равны

J

1

и J

2

. После падения

верхнего диска на нижний оба диска,

благодаря трению между ними, через

некоторое время стали вращаться как

единое целое. Найти работу

A, кото-

рую совершили при этом силы трения,

действующие между дисками.

Ответ:

2

21

)(

2

1

ωω

−

+

⋅=

JJ

A

.

Задача 2

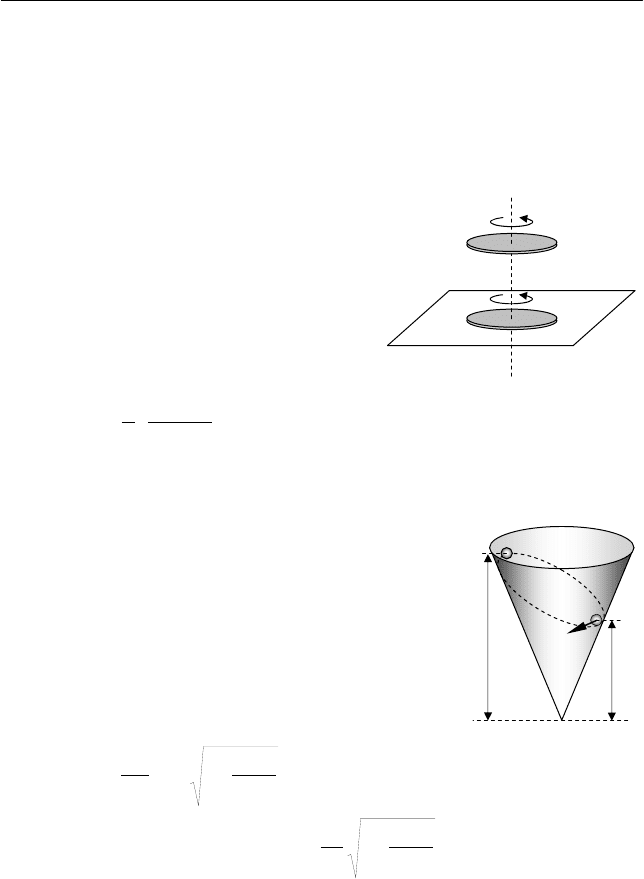
По внутренней поверхности кониче-

ской воронки, стоящей вертикально, без тре-

ния скользит маленький шарик (см. рис.). В

начальный момент времени шарик находится

на высоте

h

0

и имеет скорость

υ

0

, направлен-

ную горизонтально. На какую максимальную

высоту

h поднимется шарик в процессе дви-

жения? Чему равна его скорость

υ

на этой

высоте?

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

++=

2

0

2

0

8

11

4

υ

gh

g

h

; скорость шарика направлена гори-

зонтально и ее модуль равен:

2

0

00

8

1

2

υ

gh

+=

.

Задача 3

Тонкая палочка длиной l и массой m лежит на гладкой гори-

зонтальной поверхности. Пуля массой 8/

0

mm

=

, летевшая перпен-

J

1

J

2

ω

2

ω

1

h

0

υ

Глава 7. Законы сохранения момента импульса и механической энергии

267

дикулярно палочке и параллельно поверхности со скоростью

υ

0

,

попадает в палочку на расстоянии 4/

0

ll

=

от ее конца и застревает

в ней. Найти угловую скорость вращения системы тел после соуда-

рения.

Ответ:

l

0

13

4

υ

ω

⋅= .

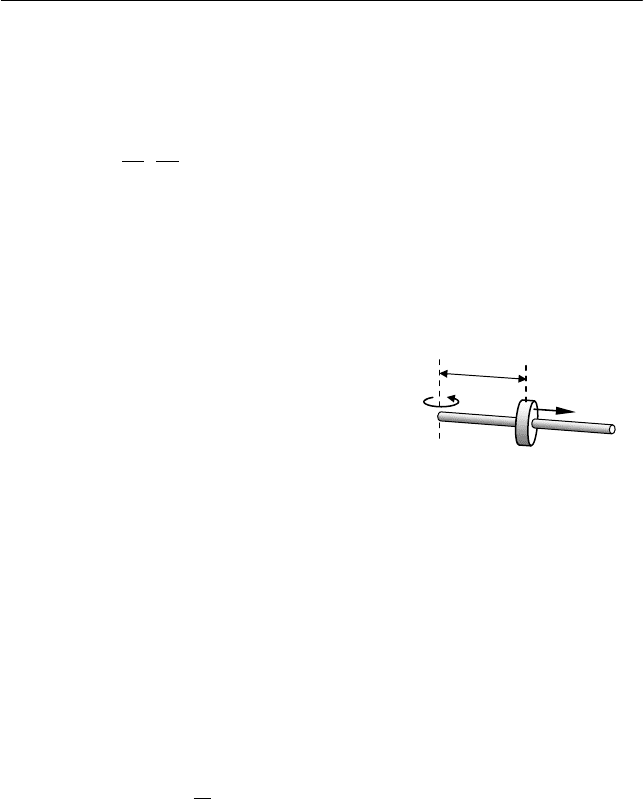
Задача 4

На гладком горизонтальном стержне, вращающемся вокруг

вертикальной оси с постоянной угловой скоростью

ω

, на расстоя-

нии l

0

от оси находится муфта массой m (см. рис.). В некоторый

момент времени муфте сообщают ско-

рость

ω

υ

00

l

=

вдоль стержня, направ-

ленную от оси вращения. Какой мо-

мент сил M должен быть приложен к

стержню для того, чтобы он продолжал

равномерное вращение? Как меняется

расстояние муфты от оси вращения в

зависимости от времени?

Ответ:

t

emltM

ω

22

2

0

2)( = ,

t

eltl

ω

0

)( = .

Задача 5

Корабль движется со скоростью

υ

= 40 км/час по дуге ок-

ружности радиуса R = 300 м. Найти момент гироскопических сил

M

Г

, действующих на подшипники двигателя корабля со стороны

ротора, который имеет момент инерции относительно оси враще-

ния J

0

= 3,6⋅10

3

кг⋅м

2

и делает n = 150 об./мин. Ось вращения распо-

ложена вдоль корабля.

Ответ:

мН101,22

3

0Г

⋅⋅==

R

nJM

υ

π

.

Задача 6

Гироскоп массой m = 0,5 кг вращается с угловой скоростью

ω

= 200 рад/с. Момент инерции гироскопа J = 5 10

-4

кг м

2

. Угловая

скорость прецессии в поле сил тяжести Земли 5,0

=

Ω

рад/с. Угол

между вертикалью и осью гироскопа

0

30=

α

. Определить расстоя-

l

0

ω

0

υ

m

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

268

ние l от точки опоры до центра масс и угловое ускорение гироско-

па.

Ответ:

==

mg

J

l

ωΩ

0,5 см,

α

Ω

ω

β

sin

=

= 50 рад/с

2

.

Задача 7

Горизонтальный желоб состоит из

двух взаимно перпендикулярных досок.

Сплошной однородный цилиндр раскру-

тили до угловой скорости

ω

и поместили

в желоб так, как показано на рисунке.

Коэффициент трения между стенками

желоба и цилиндром равен

μ

. Найти

время вращения цилиндра в желобе.

Ответ:

μ

ω

g

R

T ⋅=

4

2

.

Задача 8

Волчок массой m, опирающийся о горизонтальную поверх-

ность, вращается с угловой скоростью

ω

во-

круг своей геометрической оси (см. рис.).

Момент инерции волчка относительно ука-

занной оси равен J, расстояние от точки опо-

ры до центра масс волчка – l. Найти угловую

скорость прецессии волчка под действием

силы тяжести.

Ответ:

ω

Ω

J

mgl

= .

Задача 9

В точке A подвешены шарик на нити

длиной l и однородный стержень длиной L.

Стержень отклоняют в сторону на некоторый

угол и отпускают без начальной скорости. В

положении равновесия стержень упруго со-

ударяется с шариком. При каком соотноше-

нии между массами стержня M и шарика m

ω

mg

R

ω

l

M, L

m

A

Глава 7. Законы сохранения момента импульса и механической энергии

269

стержень после удара остановится?

Ответ:

2

3

L

l

m

M

= .

Задача 10

Частица массой m движется по эллиптической траектории

под действием центральной упругой силы

rF k

−

=

. Минимальная

скорость частицы достигается при значении ее радиус-вектора

0

rr =

относительно силового центра, совпадающего с одним из

фокусов эллипса. Найти модуль максимальной скорости частицы

max

υ

.

Ответ:

0max

r

m

k

=

υ

.

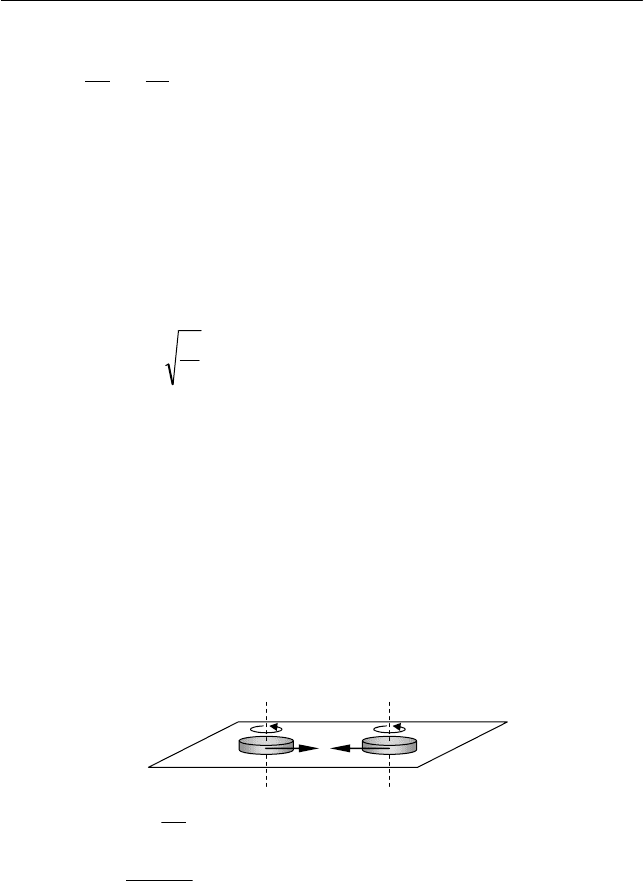
Задача 11

Две одинаковые шайбы скользят навстречу друг другу по

гладкой горизонтальной поверхности со скоростями

1

υ

и

2

υ

, вра-

щаясь с угловыми скоростями

1

ω

и

2

ω

(см. рис.). В некоторый мо-

мент времени происходит их центральное абсолютно неупругое

соударение, в результате которого шайбы начинают скользить по

поверхности и вращаться вместе. Считая известными массу m и

радиус R каждой из шайб, найти изменение кинетической энергии

шайб

k

Δ

E

и угловую скорость их вращения

ω

после соударения.

Ответ:

[]

2

21

22

2

1

22

21

k

)()(6)(6

24

Δ

ωωωωυυ

+−+++−= RR

m

E ,

6

21

ωω

ω

+

=

.

1

υ

ω

2

ω

1

2

υ

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

270

ГЛАВА 8

СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМ

С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. РЕЗОНАНС

8.1. Теоретический материал

Механические колебания – это повторяющееся ограничен-

ное движение тел механической системы относительно некоторого

своего положения. При этом обобщенные координаты, опреде-

ляющие положения тел системы в пространстве (см. п. 6.1.1 в Гла-

ве 6), ограничено изменяются около некоторого своего значения

(см. рис. 8.1).

Периодический механический процесс – движение тел ме-

ханической системы, точно повторяющееся во времени. Для систе-

мы с одной степенью свободы, этот колебательный процесс может

быть описан одной физической величиной

)(t

ξ

, периодически за-

висящей от времени (см. рис. 8.2).

Период T – минимальный интервал времени, через который

процесс в точности повторяется (рис. 8.2).

Рис. 8.2. Зависимость обобщенной координаты )(t

ξ

от

времени в случае периодического процесса

)(t

ξ

t

T

Рис. 8.1. Зависимость обобщенной координаты )(t

ξ

от

времени в случае колебаний

)(t

ξ

t

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.