Русаков В.С. и др. Механика. Методика решения задач
Подождите немного. Документ загружается.

ГЛАВА 8. Свободные и вынужденные колебания
271
Гармонические колебания – процесс, при котором физиче-
ская величина )(
t
ξ
меняется по гармоническому закону (см.
рис. 8.3).
Свободные (собственные) колебания – колебания системы,
предоставленной самой себе (при постоянных внешних условиях).
8.1.1. Собственные гармонические колебания
Уравнение собственных гармонических колебаний
, кото-
рое следует из уравнений движения механической системы, имеет
вид:
0
2
0
=+
ξωξ
&&
, (8.1)
где
ξ
– одна из обобщенных координат – независимых физиче-
ских величин, определяющих положение тел системы;
0
ω
– угло-
вая частота
и
0
0
2
ω
π
=T – период собственных гармонических ко-
лебаний, определяемые характеристиками системы.
Закон движения при собственных гармонических колебани-
ях (зависимость обобщенной координаты от времени) – решение
уравнения собственных гармонических колебаний:
()
00
cos)(
ϕ
ω
ξ
+= tAt
. (8.2)
Здесь
()
00
ϕ
ω
+t – фаза колебаний; A – амплитуда и
0
ϕ
– на-
чальная фаза
собственных гармонических колебаний, определяе-
мые
начальными условиями – значениями физической величины
()
00
tt
=
≡
ξ
ξ
и скоростью ее изменения
(
)
00
tt =≡
ξξ
&&
в начальный
момент времени t
0
:
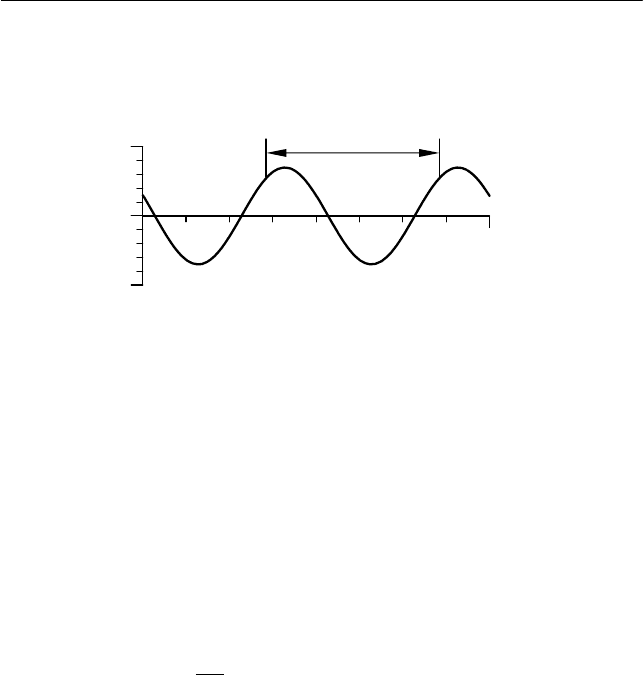
)(t
ξ
t
T
Рис. 8.3. Зависимость обобщенной координаты
)(t
ξ
от
времени в случае гармонических колебаний
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
272
2
0
0
2
0
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
ω
ξ
ξ
&
A , (8.3)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−=
00
0
000
arctg
ξω
ξ
ωϕ
&
t . (8.4)
Скорость изменения обобщенной координаты
ξ
&
(обоб-
щенная скорость
):
()
000
sin)(
ϕωωξ
+−= tAt
&
. (8.5)
Как видим, в случае гармонических колебаний амплитуды
обобщенной скорости и обобщенной координаты связаны множи-
телем
0
ω
, а фаза обобщенной скорости опережает фазу обобщен-
ной координаты на
π/2.
Необходимые условия существования собственных гармони-
ческих колебаний:
1) наличие положения устойчивого равновесия,
2) наличие возвращающей квазиупругой обобщенной силы.
В качестве примера рассмотрим колебания пружинного, ма-
тематического и физического маятников.
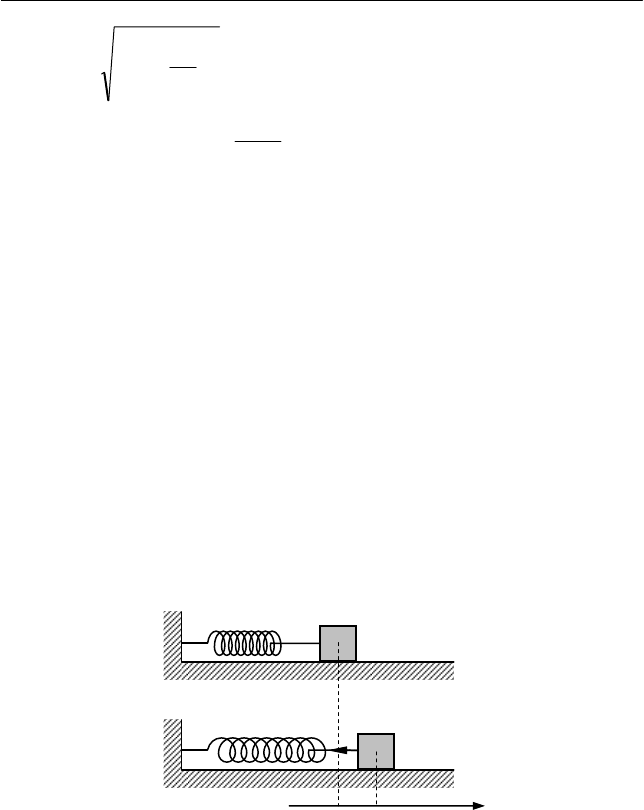
Пружинный маятник − это тело, прикрепленное к невесо-
мой пружине (см. рис. 8.4).
Рассмотрим случай горизонтального расположения пружин-
ного маятника на гладкой горизонтальной поверхности. Ось X ла-
бораторной инерциальной системы отсчета, связанной с горизон-
тальной поверхностью, направим вдоль оси пружины, а ее начало
Рис. 8.4. Пружинный маятник
m
k
упр
F
x 0 X

ГЛАВА 8. Свободные и вынужденные колебания
273
отсчета совместим с центром масс тела в положении равновесия,
соответствующего нерастянутой пружине (рис. 8.4).
На тело в процессе колебаний действует упругая сила
F
упр
со
стороны пружины, удовлетворяющая закону Гука (см.
п. 2.1. Теоретический материал в Главе 2). Уравнение движения
тела в проекции на ось X выбранной системы отсчета имеет вид:
kxxm −
=
&&
, (8.6)
где
m − масса тела, k − коэффициент жесткости пружины.
Преобразуем (8.6) к виду уравнения гармонических колеба-
ний:
0=+ x
m
k
x
&&
. (8.7)
Сравнивая (8.7) с (8.1), для угловой частоты колебаний пру-
жинного маятника получим:
m
k
=
0
ω
. (8.8)
Заметим, что при вертикальном расположении пружинного
маятника его частота не изменится. Действительно, уравнение
движения маятника в этом случае записывается в виде (8.7) при
выборе начала отсчета вертикальной координаты тела в положении
его равновесия.
Законы движения тела, прикрепленного к пружине, и изме-
нения его скорости аналогично (8.2) и (8.5) запишем в виде:
()
00
cos)(
ϕ
ω
+= tAtx , (8.9)
()
000
sin)(
ϕ
ω
ω
+
−= tAtx
&
. (8.10)
Кинетическая энергия пружинного маятника равна кинетиче-
ской энергии тела, прикрепленного к пружине:
()
=+==
00
2
2
0
2
2
k
sin
22
)(
)(
ϕω
ω
t
mA
txm
tE
&
()
00
2
2
sin
2
ϕω
+= t
kA
.
(8.11)
Потенциальная энергия пружинного маятника, расположен-
ного горизонтально, равна энергии упругой деформации пружины:
()
00
2
22
p
cos
22
)(
)(
ϕω
+== t
kAtkx
tE . (8.12)
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
274
Кинетическая и потенциальная энергии пружинного маятни-
ка изменяются в противофазе по гармоническому закону с частотой
0
2
ω
и одинаковыми амплитудами (см. рис. 8.5). Механическая
энергия пружинного маятника, равная сумме кинетической и по-
тенциальной энергий, остается постоянной в процессе колебаний:
2
)()(
2
pk
kA
tEtEE =+= . (8.13)
Математический маятник − материальная точка, подве-
шенная на невесомой нерастяжимой нити в поле сил тяжести (см.
рис. 8.6).
Рассмотрим колебания математи-
ческого маятника относительно горизон-
тальной оси, происходящие в одной
плоскости.
Выберем лабораторную инерци-
альную систему отсчета, связанную с те-
лом, к которому подвешен математиче-
ский маятник. Запишем уравнение мо-
ментов (6.39) для материальной
точки
относительно оси, проходящей через
точку подвеса перпендикулярно плоско-
сти колебаний маятника (см. рис. 8.6):
mg
M
t
L
=
d
d
, (8.14)
l
α
mg
F
Рис. 8.6. Математический
маятник
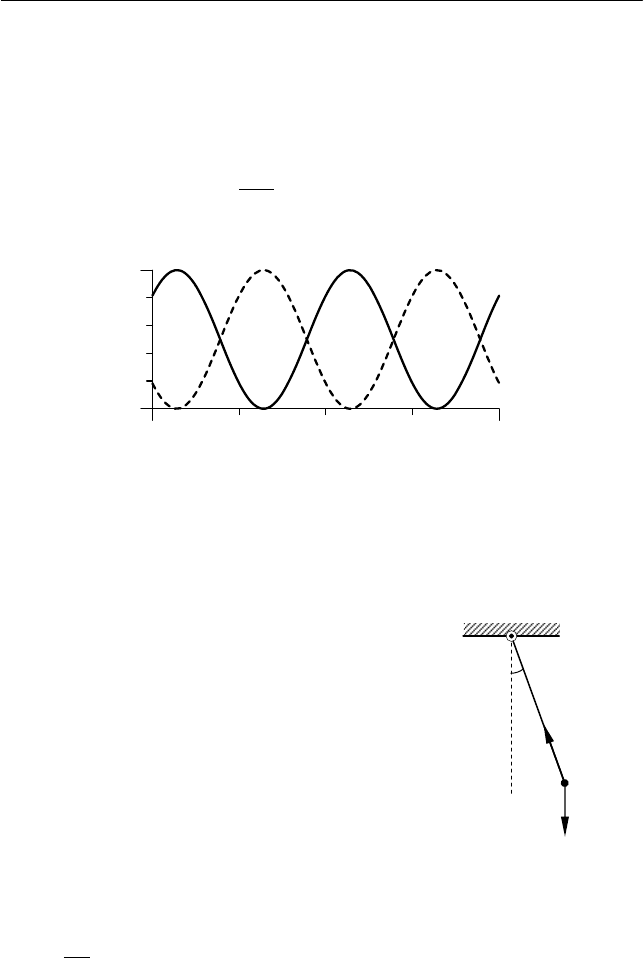
Рис. 8.5. Зависимости кинетической E
k
и потенциальной E
p
энергий маят-
ника от времени в случае собственных гармонических колебаний
0 TT/2
E
k,
p
(t)
E
k
(t) E
p
(t)
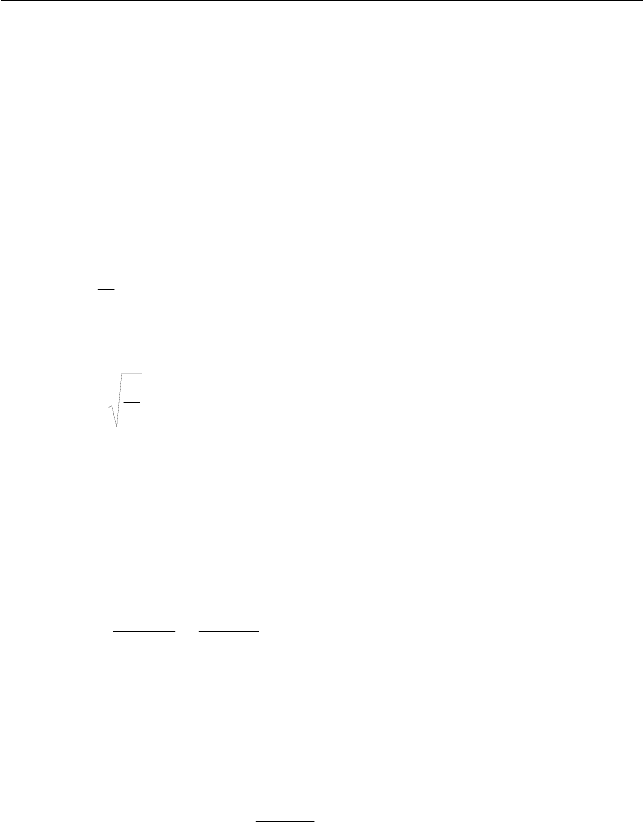
ГЛАВА 8. Свободные и вынужденные колебания
275
где
αα
&&
2
)( mlmllL == − момент импульса материальной точки от-
носительно выбранной оси,
α
− угол отклонения маятника от по-
ложения равновесия, m и l − масса и длина математического маят-
ника,
α
sinmglM
mg
−= − момент силы тяжести, действующей на
материальную точку относительно той же оси.
При малых углах отклонения маятника уравнение (8.14) сво-
дится к виду уравнения гармонических колебаний (8.1):
αα
sin
2
mglml −=
&&
, (8.15)
0=+
αα
l
g
&&
. (8.16)
Сравнивая (8.16) с (8.1), для угловой частоты колебаний ма-
тематического маятника получим:
l
g
=
0
ω
. (8.17)
Законы движения математического маятника и изменения его
угловой скорости аналогично (8.2) и (8.5) запишем в виде:
()
00
cos)(
ϕ
ω
α
+= tAt , (8.18)
()
000
sin)(
ϕ
ω
ω
α
+
−= tAt
&
. (8.19)
Кинетическая энергия математического маятника равна ки-
нетической энергии материальной точки, подвешенной на нити:
()
00
2
222
k
sin
22
ϕω
α
+== t
mglAml
E
&
. (8.20)
Потенциальная энергия математического маятника равна
энергии материальной точки в поле силы тяжести Земли. Если за
ноль отсчета потенциальной энергии принять положение равнове-
сия маятника, то его потенциальная энергия при отклонении на
угол
α
равна:
()
00
2
2
p
cos
2
)cos1(
ϕωα
+≅−= t
mglA
mglE
. (8.21)
Кинетическая и потенциальная энергии математического ма-
ятника, так же как и в случае пружинного маятника, изменяются в
противофазе по гармоническому закону с частотой
0
2
ω
и одинако-
выми амплитудами (см. рис. 8.5). Механическая энергия математи-
ческого маятника не изменяется в процессе колебаний и равна:

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
276
2
2
pk
mglA
EEE =+= .
(8.22)
Физический маятник − абсолютно твердое тело, подвешен-
ное в поле сил тяжести (см. рис. 8.7).
Рассмотрим колебания физического
маятника относительно горизонтальной оси,
в процессе которых все материальные точки
физического маятника движутся в парал-
лельных плоскостях.
Выберем лабораторную инерциальную
систему отсчета, связанную с телом, к кото-
рому подвешен физический маятник. Запи-
шем уравнение моментов (6.48)
для абсо-
лютно твердого тела относительно оси, про-
ходящей через точку подвеса перпендикулярно плоскости колеба-
ний маятника (см. рис. 8.7):
mg
MJ
=
α
&&
. (8.23)
Здесь
α
− угол отклонения маятника от положения равновесия, J −
момент инерции физического маятника относительно выбранной
оси,
α
sinmglM
mg
−= − момент силы тяжести, действующей на
материальную точку относительно той же оси, m − масса физиче-
ского маятника и l − расстояние от центра масс маятника до точки
его подвеса.
При малых углах отклонения маятника уравнение (8.23) сво-
дится к виду уравнения гармонических колебаний (8.1):
α
α
sinmglJ −
=
&&
. (8.24)
0=+
αα
J
mgl
&&
. (8.25)
Сравнивая (8.25) с (8.1), для угловой частоты колебаний фи-
зического маятника получим:
J
mgl
=
0
ω
. (8.26)
Используя теорему Гюйгенса − Штейнера (6.42), выразим уг-
ловую частоту колебаний физического маятника через его момент
инерции
0
J относительно оси, проходящей через центр масс па-
раллельно оси вращения:
Рис. 8.7. Физический
маятник
α
mg
J
0
l

ГЛАВА 8. Свободные и вынужденные колебания
277
2
0
0
mlJ
mgl
+
=
ω
. (8.27)
Заметим, что в случае математического и физического маят-
ников в качестве обобщенной координаты выступает угол отклоне-
ния маятника от положения равновесия.
Законы движения физического маятника и изменения его уг-
ловой скорости идентичны случаю математического маятника:
()
00
cos)(
ϕ
ω
α
+= tAt
, (8.28)
()
000
sin)(
ϕ
ω
ω
α
+
−= tAt
&
.
(8.29)
Кинетическая энергия физического маятника равна (см. (7.7)
в п. 7.1. Теоретический материал Главы 7):
()
00
2
22
k
sin
22
ϕω
α
+== t
mglAJ
E
&
. (8.30)
Если за ноль отсчета потенциальной энергии принять поло-
жение равновесия маятника, то его потенциальная энергия при от-
клонении на угол
α
можно записать в виде:
()
00
2
2
p
cos
2
)cos1(
ϕωα
+≅−= t
mglA
mglE . (8.31)
Механическая энергия физического маятника равна:
2
2
pk
mglA
EEE =+=
. (8.32)
8.1.2. Собственные затухающие колебания
Уравнение движения
в случае собственных затухающих ко-
лебаний имеет вид
:
02)(
2
0
=++
ξωξδξ
&&&
t , (8.33)
где
δ
– коэффициент затухания (определяется характеристиками
системы).
Решения уравнения (8.33) различны в зависимости от соот-
ношения коэффициента затухания и частоты собственных незату-
хающих колебаний.
Случай собственных затухающих колебаний
− с затуханием
меньше критического (
δ
<
ω
0
).
Закон движения в этом случае имеет вид (см. рис. 8.8):

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
278
()
0
cos)(
ϕωξ
δ
+=
−
tAet
t
. (8.34)
Здесь
22
0
δωω
−= и
22
0
22
δω
π
ω
π
−
==T –
угловая частота и пе-
риод затухающих колебаний
.
Логарифмический декремент затухания
ϑ
– логарифм от-
ношения значений обобщенной координаты в моменты времени t и
t + T:
T
Tt
t
δ
ξ
ξ
ϑ
=
+
≡
)(
)(
ln
. (8.35)
Заметим, что
ϑδ
ξ
ξ
NTN
NTt
t
==
+ )(
)(
ln . (8.36)
Обратная величина логарифмического декремента затухания
равна числу периодов, за которые амплитуда колебаний уменьшит-
ся в
7.2≅e
раз:
1
)(
)(
ln ==
+
ϑ
ξ
ξ
e
e
N
TNt
t
,
e
N=
ϑ
1
. (8.37)
Средняя механическая энергия
T
E
за период T меняется со
временем по экспоненциальному закону, поскольку потенциальная
p
E
и кинетическая
k
E
энергии механической системы квадратич-
но зависят от обобщенных координат и скоростей:
t
TT
T
eEEEE
δ
2
0
pk −
=+= . (8.38)
При этом
средняя мощность потерь
T
P равна:
)(t
ξ
t
Рис. 8.8. Зависимость обобщенной координаты )(t
ξ
от
времени в случае затухающих колебаний
ГЛАВА 8. Свободные и вынужденные колебания
279
t
T
T
T
eE
t
E
t
E
P
δ
δ
2
0
2
d
d
d
d
−
=−=−≡ . (8.39)
Добротность колебательной системы Q определяется от-
ношением средней за период механической энергии системы к
средней мощности потерь:
δ
ω
ϑ
π
δ
π
δ
ππ
δ
δ
2
2
22
2
0
2
0
====≡
−
−
T
TeE
eE
TP
E
Q
t
t
T
T
. (8.40)
Случай апериодического движения − с затуханием больше
критического (
δ
>
ω
0
).
Закон движения в этом случае записывается в виде:
tt
eAeAt
⎟
⎠
⎞
⎜
⎝
⎛
−−−
⎟
⎠
⎞
⎜
⎝
⎛
−+−
+=
2
0
22
0
2
21
)(
ωδδωδδ
ξ
, (8.41)
где A
1
и A
2
– постоянные величины, определяемые начальными ус-
ловиями.
В зависимости от начальных условий постоянные величины
A
1
и A
2
могут быть как одного, так и разных знаков.
При
0
2
1
>
A
A
обобщенная координата )(t
ξ
монотонно стре-
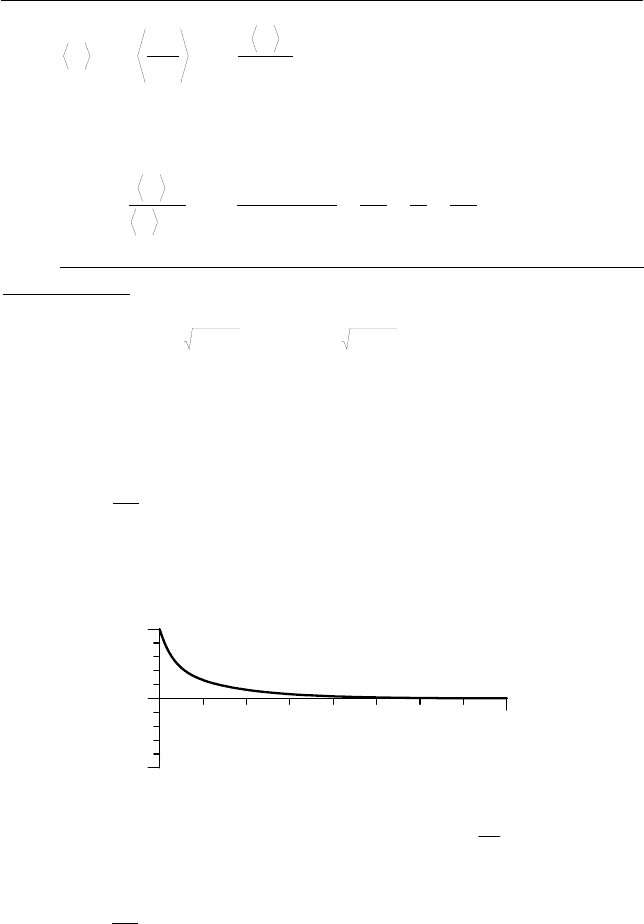
мится к нулю при ∞→t (см. рис. 8.9).
При
0
2
1
<
A
A
обобщенная координата )(t
ξ
в некоторый мо-
мент времени обращается в ноль, затем достигает локального экс-
)(t
ξ
t
Рис. 8.9. Зависимость обобщенной координаты )(t
ξ
от времени
в случае апериодического движения при
0
2
1
>
A
A

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
280
тремума и далее монотонно стремится к нулю при ∞→t (см.
рис. 8.10).
Случай критического затухания
(
δ
=
ω
0
).
Закон движения в этом случае имеет вид:
t
etAAt
δ
ξ
−
+= )()(
21
, (8.42)
где A
1
и A
2
– постоянные величины, определяемые начальными ус-
ловиями.
Возможные виды зависимости обобщенной координаты от
времени при различных начальных условиях изображены на
рис. 8.11.
Независимо от соотношения коэффициента затухания
δ
и
частоты собственных незатухающих колебаний
0
ω
обобщенная
координата )(t
ξ
стремится к нулю при
∞
→t .
)(t
ξ
t
Рис. 8.10. Зависимость обобщенной координаты
)(t
ξ
от време-
ни в случае апериодического движения при
0
2
1
<
A
A
)(t
ξ
t
Рис. 8.11. Зависимость обобщенной координаты )(t
ξ
от
времени в случае критического затухания
