Russ J.C. Image Analysis of Food Microstructure

Подождите немного. Документ загружается.

grey cell and another (

β−β

), and between a white and a grey cell (

α−β

). The presence

of many different phases and types of interfaces is common in food products.

By either manual procedures or by using the methods of image processing

discussed in subsequent chapters, the individual phases and interfaces can be isolated

and measured, grids generated, and intersections counted. Table 1.2 shows the

TABLE 1.2

Surface Area Measurements from Figure 1.16

Boundary

Type

Intersection

Counts

Cycloid length

(µm)

= 2•P

(µm

–1

)

Boundary Length

(µm)

Image Area

(µm

)

= 4/•B

(µm

–1

)

α–α 24 360 0.133 434.8 4500 0.123

α–β 29 360 0.161 572.5 4500 0.162

β–β 9 360 0.050 117.8 4500 0.033

(a)

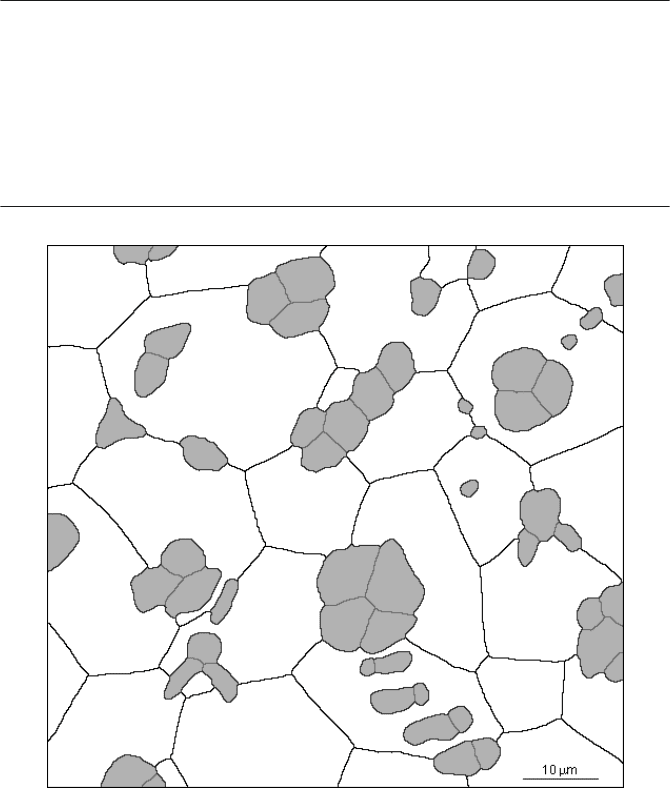
FIGURE 1.16 (See color insert following page 150.) Measurement of surface area. A two-

phase microstructure is measured by (a) isolating the different types of interface (shown in

different colors) and measuring the length of the curved lines; and (b) generating a cycloid

grid and counting the number of intersections with each type of interface. The reason for

using this particular grid is discussed in the text.

2241_C01.fm Page 23 Thursday, April 28, 2005 10:22 AM

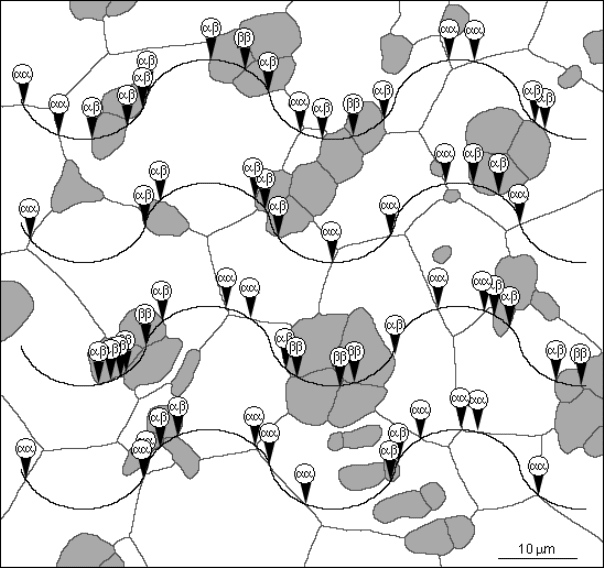
speciﬁc results from the measurement of the length of the various boundary lines

and from the use of the particular grid shown. The numerical values of the results

are not identical, but within the expected variation based on the precision of the

measurements and sampling procedure used.

Note that the units of P

, B

and S

are all the same (length

–1

). This is usually

reported as (area/volume), and to get a sense of how much surface area can be

packed into a small volume, a value of 0.1 µm

–1

corresponds to 100 cm

/cm

, and

values for S

substantially larger than that may be encountered. Real structures often

contain enormous amounts of internal surface within relatively small volumes.

For measurement of volume fraction the image magniﬁcation was not important,

because P

, L

, A

and V

are all dimensionless ratios. But for surface area it is

necessary to accurately calibrate image magniﬁcation. The need for isotropic sam-

pling is still present, of course. If the section planes have been cut with orientations

that are randomized in three dimensions (which turns out to be quite complicated

to do, in practice), then circles can be drawn on the images to produce isotropic

sampling in three dimensions.

(b)

FIGURE 1.16 (continued)

2241_C01.fm Page 24 Thursday, April 28, 2005 10:22 AM

One approach to obtaining isotropic sampling is to cut the specimen up into

many small pieces, rotate each one randomly, pick it up and cut slices in some

random orientation, draw random lines on the section image, and perform the

counting operations. That works, meaning that it produces results that are unbiased

even if the sample is not isotropic, but it is not very efﬁcient. A better method,

developed nearly two decades ago, generates an isotropic grid in 3D by canceling

out one orientational bias (produced by cutting sections) with another. It is called

the method of “vertical sections” and requires being able to identify some direction

in the sample (called “vertical” but only because the images are usually oriented

with that direction vertical on the desk or screen). Depending on the sample, this

could be the direction of extrusion, or growth, or the backbone of an animal or stem

of a plant. The only criterion is that the direction be unambiguously identiﬁable.

The method of vertical sections was one of the ﬁrst of the developments in what

has become known as “unbaised” or design-based stereology.

Section planes through the structure are then cut that are all parallel to the vertical

direction, but rotated about it to represent all orientations with equal probability

(Figure 1.17). These planes are obviously not isotropic in three-dimensional space,

since they all include the vertical direction. But lines can be drawn on the section

plane images that cancel this bias and which are isotropic. These lines must have

sine-weighting, in other words they must be uniformly distributed over directions

based not on angles but on the sines of the angles, as shown in the ﬁgure. It is

possible to draw sets of straight lines that vary in this way, but the most efﬁcient

procedure to draw lines that are also uniformly distributed over the surface is to

generate a set of cycloidal arcs.

The cycloid is a mathematical curve generated by rolling a circle along a line

and tracing the path of a point on the rim (it can be seen as the path of a reﬂector

on a bicycle wheel, as shown in Figure 1.18). The cycloid is exactly sine weighted

and provides exactly the right directional bias in the image plane to cancel the

orientational bias in cutting the vertical sections in the ﬁrst place. Cycloidal arcs

can be generated by a computer and superimposed on an image. The usual criteria

for independent sampling apply, so the arcs should be spaced apart to intersect

different bits of surface line, and not so tightly curved that they resample the same

segment multiple times. They may be drawn either as a continuous line or separate

arcs, as may be convenient. Figure 1.18 shows some examples.

The length of one cyloidal arc (one fourth of the full repeating pattern) is exactly

twice its height (which is the diameter of the generating circle), so the total length

of the grid lines is known. Counting the intersections and calculating S

using

Equation 1.7 gives the desired measure of surface area per unit volume, regardless

of whether the structure is actually isotropic or not. Clearly the cutting of vertical

sections and drawing of cycloids is more work than cutting sections that are all

perpendicular to one direction (the way a typical microtome works) and using a

simple straight-line grid to count intersections. Either method would be acceptable

for an isotropic structure, but the vertical section method produces unbiased results

even if the structure has preferred orientation, and regardless of what the nature of

that anisotropy may be.

2241_C01.fm Page 25 Thursday, April 28, 2005 10:22 AM

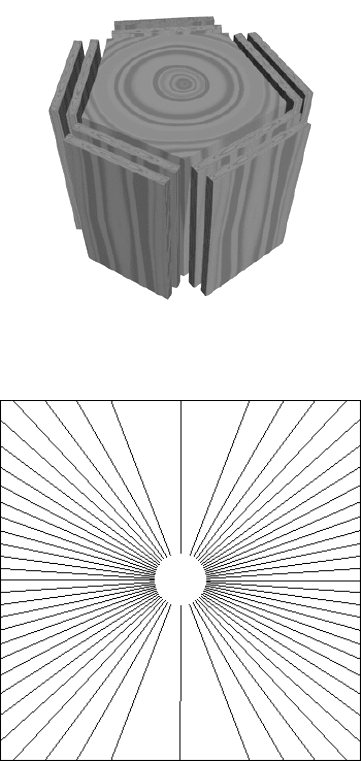
(a)

(b)

FIGURE 1.17 The method of vertical sections: (a) a series of slices are cut lying parallel to

an identiﬁable direction, but rotated to different angles about that direction; (b) on each slice,

lines that are sine-weighted (their directions incremented by equal steps in the value of the

sine of the angle) are drawn. These lines isotropically sample directions in three dimensional

space.

2241_C01.fm Page 26 Thursday, April 28, 2005 10:22 AM

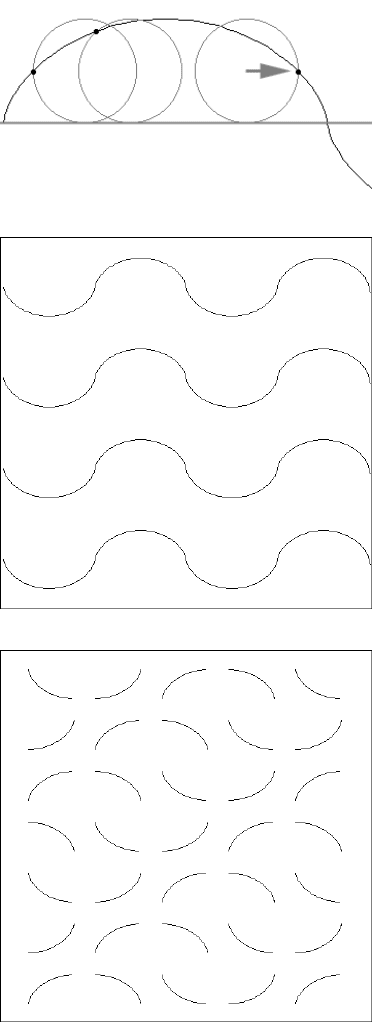
(a)

(b)

(c)

FIGURE 1.18 Cycloid grids: (a) generation of a cycloid as the path traced out by a point on

the rim of a rolling circle; (b) a set of continuous cycloid grids; (c) a set of separated cycloid arcs.

2241_C01.fm Page 27 Thursday, April 28, 2005 10:22 AM

LINES AND POINTS

The preceding sections have described the measurement of volumes and surfaces

that may be present in 3D structures. These are, respectively, 3- and 2-dimensional

features. There may also be 1- and 0-dimensional features present, namely lines and

points. Surfaces were considered to include extremely thin interfaces between

phases, as well as ﬁnite membranes around objects. Similarly, a linear structure may

have ﬁnite thickness as long as its lateral dimensions are very small compared to

its length and the size of the other structures with which it interacts. So the veins

or nerves in meat, and the various kinds of ﬁbers in either natural or man-made

foods are all linear structures.

A thicker structure, such as the network of particles that form in gels (e.g.,

polysaccharides such as pectin or alginates), shortening and processed meats, may

also be considered as a linear structure for some purposes, as can a pore network.

In both cases, we imagine the lateral dimensions to shrink to form a backbone or

skeleton of the network, which is then treated as linear for purposes of measurement.

Note that a linear structure may consist of a single long line, many short ones, or a

complex branching network. The topology of structures is considered later, at the

moment only the total length is of concern.

In addition, a line exists where two surfaces meet, as indicated in Figure 1.19.

One of the simplest examples of these edge lines is the structure of a bubble raft

such as the head on beer. Except for the bubbles on the outside of this raft, whose

surfaces are curved, all of the soap ﬁlms that separate bubbles from each other are

ﬂat planes. This is the equilibrium structure of many solid materials as well, ranging

from grains in metals to cells in plants. The boundaries of each facet where three

planes meet are lines, and can be treated as an important component of the structure.

It is these triple lines where much of the diffusion of gases and ﬂuids occurs, for

example, or which are responsible for the mechanical strength of a ﬁber network.

Linear structures appear as points in a section plane, where the plane intersects

the line. In many real cases the lateral dimension of the linear structure is small but

still large enough that the intersections appear as small features in the image. These

FIGURE 1.19 Diagram of a cell or bubble structure (with the topmost cell removed for

clarity) showing the triple lines (a) where three cells meet and the quadruple points (b) where

four cells meet.

2241_C01.fm Page 28 Thursday, April 28, 2005 10:22 AM

are simply counted. The total length of the linear structure per unit volume L

material is calculated from the number of intersection points per unit area P

(1.8)

where P is the number of points of intersection, A is the area of the image, and (2)

is a geometrical constant, as above, that compensates for the range of orientations

with which the section plane can intersect the lines.

As for the measurement of surfaces, discussed above, the measurement of line

length must be concerned with directionality. If the sample is not isotropic, then the

probes must be. In this case the probes are the section planes, and it was noted above

that producing an isotropic array of section planes is very difﬁcult, inefﬁcient, and

wasteful of material. There is a useful technique that can use the method of vertical

sections to simplify the procedure.

Thus far, measurements have been made on plane sections cut through surfaces.

Either the material has been considered as opaque so that a true plane surface is

examined, or in the case of transmission microscopy, the section thickness has been

assumed to be very thin as compared to the dimensions of any of the structures of

interest. But in many cases the food products of interest are at least somewhat

transparent and it is possible to obtain images by shining radiation (light, electrons,

or something more exotic) through a moderately thick slice. The resulting image

shows a projection through the structure in which linear features can be seen.

Simply measuring the length of the lines will not sufﬁce, however. There is no

reason to expect them to all lie ﬂat in the plane of the section, so that their true

length can be measured, and there is likewise no reason to expect them to be isotropic

in direction so that a geometric constant can be used to convert the total measured

projected length to an estimate of the true length in 3D.

But another approach is possible. Imagine drawing a line on the image. That

line represents a plane in the original thick slice sample that extends down through

the thickness of the slice, as shown in Figure 1.20. Counting the number of inter-

sections of the linear structure with the drawn line (which implies their intersection

with the plane the line represents) gives a value of P

(number of counts per unit

area of plane). The area of the plane is just the length of the line drawn on the image

times the thickness of the section, which must be known independently. Then the

same relationship introduced above (Equation 1.8) can be used.

In order to obtain isotropic orientation of the plane probes (not the section planes,

but the thru-the-slice planes that correspond to the lines drawn on the image), it is

necessary to use the vertical sectioning approach. All of the slices are cut parallel

to some assumed vertical orientation and rotated about it. Then the lines are drawn

as cycloids, representing a cycloidal cylindrical surface extending down through the

section thickness. Because in this case it is the orientation of the surface normals

of those probe surfaces that must be made isotropic, it is necessary to rotate the grid

of cycloid lines by 90 degrees on the image, as shown in Figure 1.21.

Finally, there are many structures in which the features of interest are small in

dimension as compared to the scale of the image and of surrounding structures.

=⋅2

2241_C01.fm Page 29 Thursday, April 28, 2005 10:22 AM

FIGURE 1.20 Linear structures in a thick section can be measured by counting the number

of intersections they make with a plane extending through the section thickness, represented

by a line drawn on the projected image.

FIGURE 1.21 Measuring the length per unit volume of tubules in a thick section, by drawing

a cycloid grid and counting the number of intersections.

2241_C01.fm Page 30 Thursday, April 28, 2005 10:22 AM

These are typically called “points.” Points also mark the locations where lines meet

planes, such as a linear structure penetrating a boundary, or even four planes meeting

(the quadruple points that exist in a tessellation of grains or cells where four cells

meet). A section plane through the structure will not intersect any true points, so it

is not possible to learn anything about them from a plane or thin slice. But if they

are visible in the projected transmission image from a thick slice they can be counted.

Provided that the number of points is low enough (and they are small enough) that

their images are well dispersed in the image, then simple counting with produce P

directly, where V is the volume (area times thickness) of the slice imaged, and P is

the observed number of points.

DESIGN OF EXPERIMENTS

Given a specimen, or more typically a population of them, what procedure should

be followed to assure that the measurement results for area fraction, surface area

per unit volume, or length per unit volume are truly representative? In most situations

this will involve choosing which specimens to cut up, which pieces to section, which

sections to examine, where and how many images to acquire, what type of grid to

draw, and so forth. The goal, simply stated but not so simply achieved, is to probe

the structure uniformly (all portions equally represented), isotropically (all directions

equally represented) and randomly (everything has an equal probability of being

measured). For volume or point measurements, the requirement for isotropy can be

bypassed since volumes and points, unlike surfaces and lines, have no orientation,

but the other requirements remain.

One way to do this, alluded to above, is to achieve randomization by cutting

everything up into little bits, mixing and tumbling them to remove any history or

location or orientation, and then select some at random, microtome or section them,

and assume that the sample has been thoroughly randomized. If that is the case,

then any kind of grid can be used that doesn’t sample the microstructure too densely,

so that the locations sampled are independent and the relationship for precision

based on the number of events counted holds. To carry the random approach to its

logical conclusion, it is possible to draw random lines or sprinkle random points

across the image. In fact, if the structure has some regularity or periodicity on the

same scale as the image, a random grid is a wise choice in order to avoid any bias

due to encountering a beat frequency between the grid and the structure.

But random methods are not very efﬁcient. First, the number of little bits and

the number of sections involved at each step needs to be pretty large to make the

lottery drawing of the ones to be selected sufﬁciently random. Second, any random

scheme for the placement of sections, ﬁelds of view or grids, or the selection of

samples from a population, inevitably produces some clustering that risks oversam-

pling of regions combined with gaps that undersample other areas.

The more efﬁcient method, systematic (or structured) random sampling, requires

about one-third as much work to achieve comparable precision, while assuring that

IUR (Isotropic, Uniform, Random) sampling is achieved. It starts, as does any design

of experiments, by making a few preliminary measurements to allow estimating the

2241_C01.fm Page 31 Thursday, April 28, 2005 10:22 AM

number of samples, sections, images, etc. that will be required to achieve the desired

precision.

Let us say by way of example that we wish to measure the amount of surface

area per unit volume in a product, for which we have 12 specimens. After considering

the need to compare these results to others of products treated differently, we decide

that the results needs to be measured to 3% precision. That means we need at least

1000 events (hits made by the sampling line probes — the grid — with the lines in

the image that represent the surface in the 3D structure) for each population, because

the square root of 1000 is about 32, or 3%.

To get those 1000 hits, we could cut a single section from a single specimen

and measure many ﬁelds of view with a grid containing many lines, but it seems

very dangerous to assume that one individual specimen is perfectly representative

of the population, or that one section orientation is an adequate sampling of the

structure. But on the other hand, we certainly want to look at as few specimens as

possible and cut as few sections as practical.

Examining a few randomly selected images (or perhaps prior experience with

other similar products) suggests that with a fairly sparse grid (so that there is no

danger of oversampling), a typical ﬁeld of view will produce about 10 hits. That

means we need to look at no fewer than 100 ﬁelds of view. How should these be

distributed over the available samples?

The variables we can choose are the number of specimens to cut up (N ), the

number of vertical section orientations to cut in each (V ), the number of slices to

cut at each orientation (S), and the number of ﬁelds of view to image on each slice

(F ). The product of N·V·S·F must be at least 100. There is a different cost to each

variable, with F being much quicker, cheaper and easier than V, for example. And

some variables have natural limits — clearly N must be larger than 1 but no greater

than 12, and it is usual to select V as an odd number, say 3 or 5, rather than an even

one in order to avoid any effects of symmetry in the sample. This is perhaps slightly

more important for natural products, which tend to grow with bilateral symmetry,

than man-made ones.

One choice that could be made would be N = 3, V = 3, S = 4, F = 3 (a total of

108 ﬁelds). Since we observe (in this example) that about half of each slide actually

contains sample, and half is empty, we will double the number of ﬁelds to F = 6 to

compensate. Other choices are also possible, but usually the various factors will

tend to be of similar magnitudes. Based on this choice, how should the three

specimens, location of the various ﬁelds of view, etc., be carried out?

That is where the systematic random part of the procedure comes in. We want

uniform but random coverage, meaning that every possible ﬁeld of view in every

possible slice in every possible orientation of every possible specimen has an equal

chance of being selected, even if only a few of them actually will be. The procedure

is the same at every stage of the selection process. Starting with the 12 specimens

in the population, we must choose N = 3. Twelve divided by three is four, so we

begin by generating a random number (in the computer or by spinning a dial) between

1 and 4. The specimen with that number is selected, and then every fourth one after

it. The basic principle is shown in Figure 1.22. This procedure distributes the

selection uniformly across the population but randomizes the placement.

2241_C01.fm Page 32 Thursday, April 28, 2005 10:22 AM