Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.


114
ANTHONY
R.
HANSEN
1983/ 1984
were used, These data were objectively analyzed from observa-
tions with a multivariate optimum interpolation scheme (Lorenc,
198
1)
and
were balanced with a normal mode initialization technique (Temperton and
Williamson,
198
1
;
Williamson and Temperton,
198
1).
Further discussion of
the data handling procedures used at ECMWF as well as the potential short-
comings of the data can be found, for example, in Hoskins
et
al.
(1
983).
The
major problem with the data is the attenuation of the divergent wind in the
tropics caused by difficulties in incorporating diabatic heating in the initiali-
zation procedure. In the present study, we are concerned with midlatitude
phenomena
so
this will not be a problem. In general, it is widely believed that
the
ECMWF
analyses have the highest accuracy of any currently available
global dataset (e.g., Hoskins
et
af.,
1983).
As
the balanced initial fields of an
operational model, they are necessarily model dependent, but the fact that
they include assimilated data from numerous sources in addition to conven-
tional radiosondes (e.g., satellite soundings and aircraft reports over the
oceans) and that they are a three-dimensionally balanced dataset largely
compensates the disadvantage of model dependency. In addition, in the
present study we will be primarily interested in differences between ensem-
bles of fields within the dataset
so
we do not have serious reservations about
the data source.
4.2.
Energetics
and Enstrophy Budget
4.2.1.
Formulation.
The technique of computing the energetics of the
atmosphere using a zonal harmonic representation of the basic-state vari-
ables
was
developed by Saltzman
(1957).
The strength
of
this technique lies
in decomposition of the longitudinal variance of these variables in midlati-
tudes into contributions from different wavelength features.
As
such, it can
yield useful information about the energy cycle for the various zonal har-
monic waves and has been used in innumerable diagnostic studies. Its draw-
back is that it yields only mass-averaged results and does not explicitly
account for variance in the meridional direction.
As
such, regionally local-
ized processes may be masked in the spectral results, although if a localized
process is sufficiently intense, it will leave a marked signature in the averaged
results (Hansen and Chen,
1982).
Since we are investigating a phenomenon
whose spatial amplitude variations are primarily oriented in the east
-
west
direction, the zonal harmonic representation of the data is the most appro-
priate for our purposes.
The formulation of the spectral energetics equations is given by Saltzman
(1
970)
and Tomatsu
(1979).
In symbolic
form,
the rates of change of wave-

ATMOSPHERIC PLANETARY
WAVE
CHARACTERISTICS
115
number
rn
kinetic energy
(K,)
and available potential energy
(A,)
are given
by
(J/Jt)Krn
=
C(Kz,
Krn)
+
C(Am,
Km)
+
CdmIn,
Z)
+
F(Km)
+
J‘(@rn)
+
D(Km)
(J/Jt)Am
=
C(Az,
Am)
-
C(Am,
Km)
+
CA(mIn,
1)
+
G(Am)
+
J’(Arn)
Here, a
z
subscript denotes a zonal mean quantity
(
)z
=
&
r(
)
d
1
where
1
=
longitude
and an
rn
subscript denotes a departure from this mean for wavenumber
m.
The notation
C(A,
B)
represents a conversion of energy from reservoir
A
to
reservoir
B.
The term
Cx(rnln,
Z)
denotes the rate of increase of the quantity
X
(where
X
=
K
or
A)
at wavenumber
rn
due to nonlinear triad interactions
with all possible combinations of wavenumben
n
and
1.
Terms
F(K,)
and
F(&)
denote the combined horizontal and vertical
boundary fluxes of
K,
and
A,,
respectively, and
F(0,)
is the boundary flux
of geopotential energy. The kinetic energy dissipation
D(K,)
will be esti-
mated
as
a residual. The generation ofavailable potential energy,
G(A,),
was
not computed but it will generally make a negative contribution (Brown,
1964).
The
G(A,)
could be estimated
as
a residual also.
Similarly, the rate of change of wavenumber
rn
enstrophy
(Em)
can be
written as
(a/at)Em
=
C(Ez,
Em)
+
C~(mln,
I)
+
Pm
+
G(Em)
+
T(Ern)
+
F(Em)
+
D(Em)
The enstrophy equation is derived from the equation for the vertical compo-
nent of the atmosphere’s vorticity. The notation follows that in the energy
equations except that
/?,
represents the P-effect
(-v
*
Of)
from the vorticity
equation. The term
C(E,,
Em)
represents the wave-mean flow interaction,
C,(mln,
I)
represents the wave-wave interactions, and
F(E,)
and
D(E,)
are, respectively, the boundary fluxes and the dissipation of enstrophy. En-
strophy generation,
G(E,),
is due to the vortex stretching mechanism that
results from divergent motions. The
T(E,)
represents the effect on the
enstrophy budget
of
the twisting and tilting term in the vorticity equation. It
is
a transfer of vorticity (and therefore enstrophy) from the horizontal com-
ponents to the vertical component. The
G(E,)
represents the major source
of enstrophy in midlatitudes. The contribution due to
T(E,)
is
generally

I16
ANTHONY
R.
HANSEN
small and was not computed in the present study. The formulation of the
spectral enstrophy equation can be found in Chen (1985).
The terms in these equations were integrated from
20”N
to 80”N and
from
1
OOO
to
100
mb. The zonal harmonic representation of the basic state
variables was truncated at
m
=
20.
Each
of
the terms in these budget equations was evaluated for each day of
our four-winter dataset. Using the wave amplitude probability density dis-
tribution
as
a guide (Sutera, 1986), each observation was assigned to the
Mode
1
or Mode
2
sample depending upon the value of
[Z2-,]
on that day.
The mean energetics presented below represent an arithmetic average over
all of the days in each mode. In addition, the ensemble mean fields for each
of
the two modes were computed for each winter from which the “stationary”
contribution to the energetics of each mode was computed.
A
weighted average ofthe individual year’s mean stationary contributions
was then computed
as
follows:
4
(
$1
=
2
@(
):)
where
w{J)
is
the number
of
days in mode
j
during the ith winter (Table
I)
divided by the total number
of
mode
j
days in the four winters,
(
)$I
is
the
stationary part of a given budget term for thejth mode in the ith winter, and
(
T)
is
the
4-yr
mean value of the given stationary term for mode
j.
This
approach was used to reduce the influence of interannual variability on the
computation of the stationary contribution.
If
the stationary contributions
are computed simply by averaging the basic state variables over the four
winters for each mode and then computing the energetics, the stationary
contributions are uniformly smaller
(20-
50% smaller for Mode
I
and
20%
smaller for Mode
2)
because the variance associated with the interannual
variability is then represented in the transient components of the budget
terms.
i-
1
4.2.2.
Energetics
for
Each
Mode.
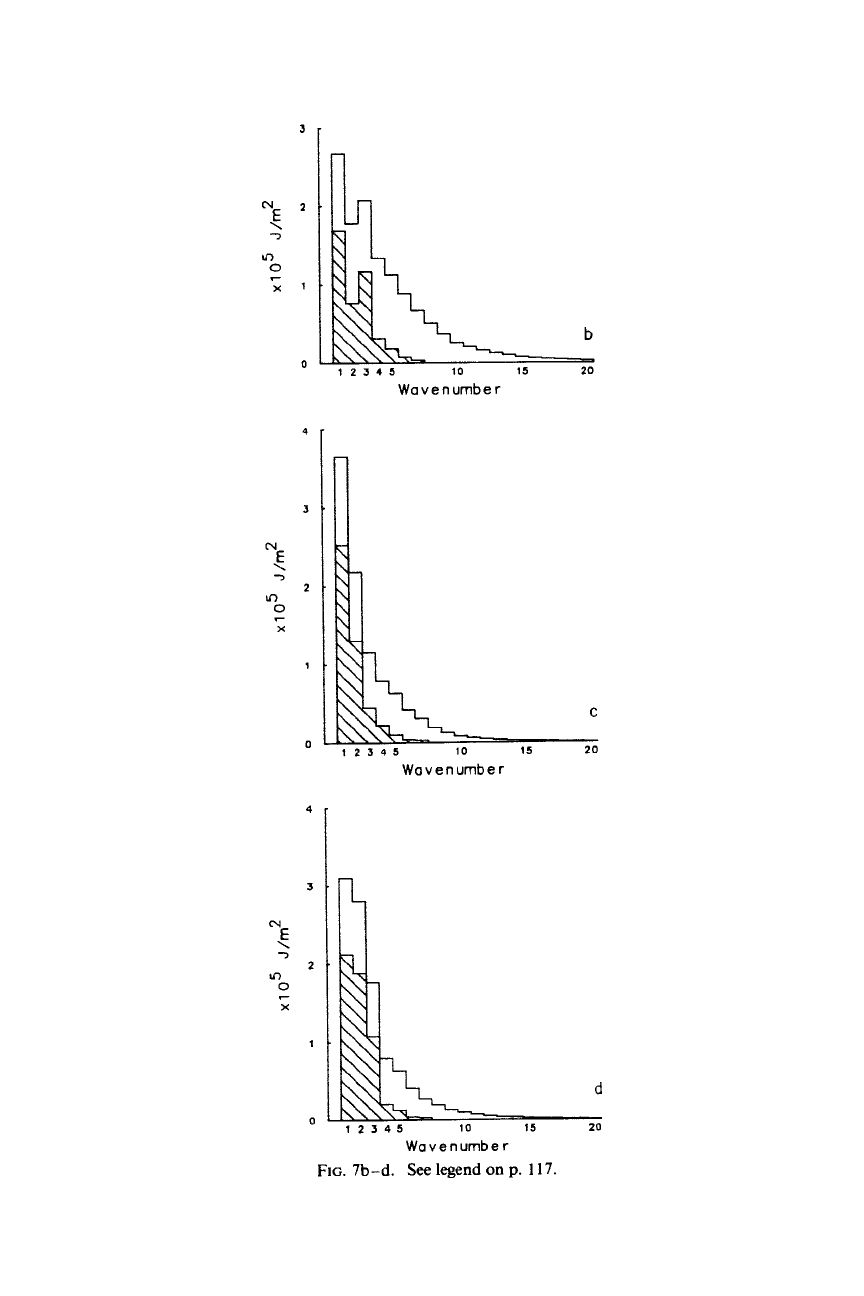
First consider the kinetic energy and
available potential energy spectra for the two modes (Fig.
7).
(In this and
subsequent figures, stationary contributions are denoted by the shading.)
Notice that the total
K,
for wavenumbers
2-4
increases markedly for
Mode
2,
with doubling of the stationary contributions to waves
2
and
3
(see
summary in Table
11).
This results in a more steeply sloped
K,,,
spectrum at
its low-wavenumber end. The
A,
spectrum also exhibits large increases in
the total and stationary
A,
for wavenumbers
2
and
3.
The overall increase in
Kz-4
(=
X:f-2
rU,)
for Mode
2
compared to Mode
1
is
30%,
with
92%
of
this
due to the stationary component, while
A2-4
increases
32%
for Mode
2,
with
92%
of the increase contributed by the stationary part.
ATMOSPHERIC PLANETARY WAVE CHARACTERISTICS
117
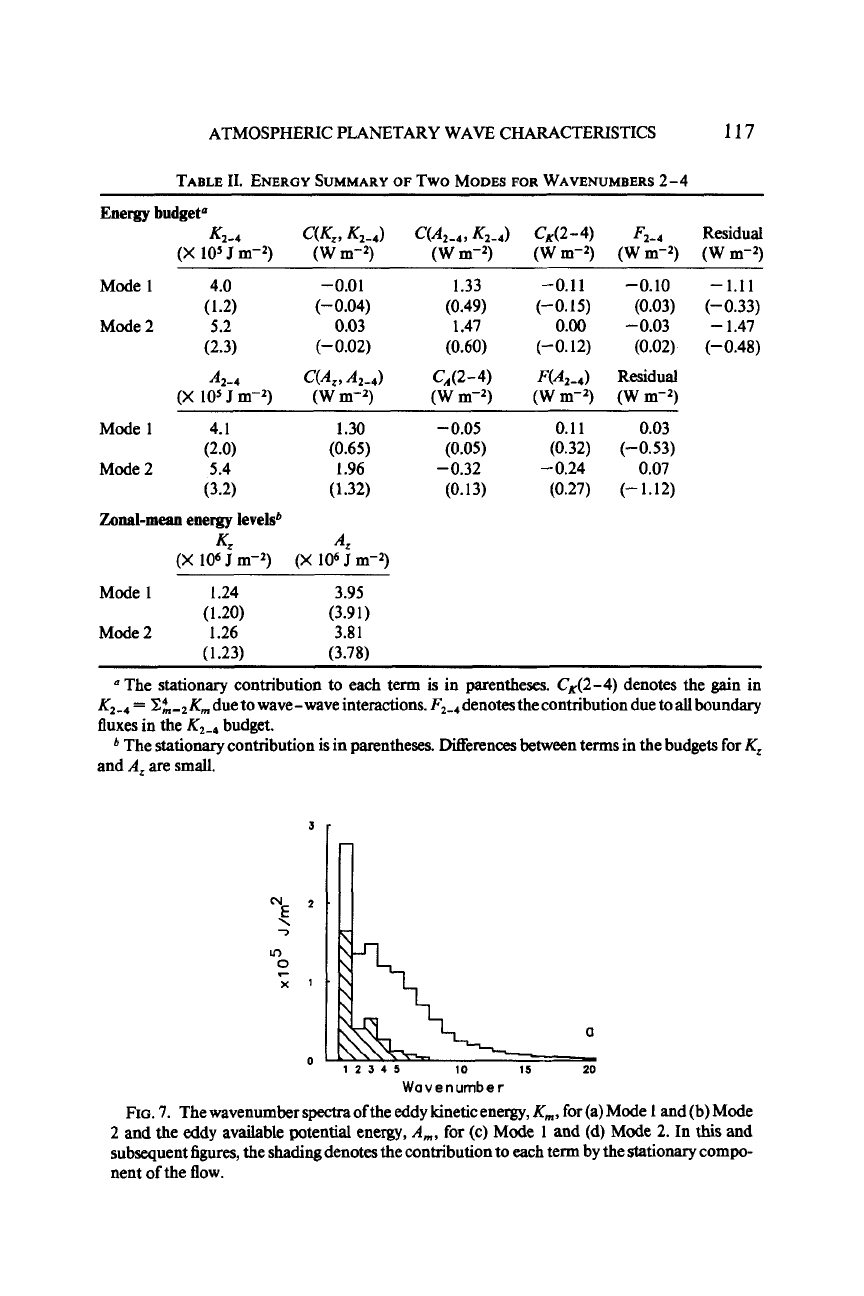
TABLE
11.
ENERGY SUMMARY
OF
Two MODES
FOR
WAVENUMBERS
2-4
Energy
budgeta
K2-4
CW,, KZ-4)
C(A2-.,, KZ-4)
Cd2-4)
F2-4
Residual
(X
lo5
J
m-3
(W
w2)
(W
rn-3
(W
w2)
(W
nr2)
(W
m-2)
Mode
I
4.0
-
0.0
1
1.33 -0.11
-0.10
-1.11
Mode
2
5.2
0.03
1.47
0.00
-0.03
-
1.47
(
1
.2)
(-0.04)
(0.49) (-0.15)
(0.03) (-0.33)
(2.3)
(-0.02)
(0.60)
(-0.12)
(0.02)
(-0.48)
A2-4
C(A,,
A2-4)
CA(2-4)
F(A2-4) Residual
(X
105J
m+)
(W
w2)
(W
nr2)
(W
c2)
(W
m2)
Mode
1
4.1 1.30 -0.05
0.1
1 0.03
Mode
2 5.4 1.96 -0.32
-
0.24 0.07
Zonal-mean
energy levelsb
(2.0) (0.65)
(0.05) (0.32)
(-0.53)
(3.2) (1.32)
(0.13)
(0.27)
(-
1.12)
4
A,
(X
lo6
J
m-2)
(X
lo6
J
m2)
Mode
1
1.24 3.95
(1.20) (3.91)
Mode
2 1.26 3.81
(1.23) (3.78)
a
The stationary contribution to each term is in parentheses.
CK(2-4)
denotes the gain
in
K2-4
=
Xi-zK, due
to
wave-wave interactions. F,-,denotes the contribution due to allboundary
fluxes in the Kz-4 budget.
*
The stationary contribution
is
in parentheses. Differences between terms in the budgets for K,
and
A,
are
small.
0
12345
10
15
20
Wavenumber
FIG.
7.
The wavenumber
spectra
of the eddy kinetic energy, K,,,
,
for (a) Mode
1
and (b) Mode
2
and the eddy available potential energy,
A,,,,
for (c) Mode
1
and (d) Mode
2.
In
this
and
subsequent figures, the
shading
denotes the contribution to
each
term by the stationary compo-
nent of the flow.
N
E
\
-3
ro
0
7
X
Wovenumber
"[
3
N
E
\
-¶
m
2
0
c
X
1
0
Wavenumber
41
N
E
\
7
m
0
7
X
Wovenumber
FIG.
7b-d.
See
legend
on
p.
117.
ATMOSPHERIC PLANETARY WAVE CHARACTERISTICS
119
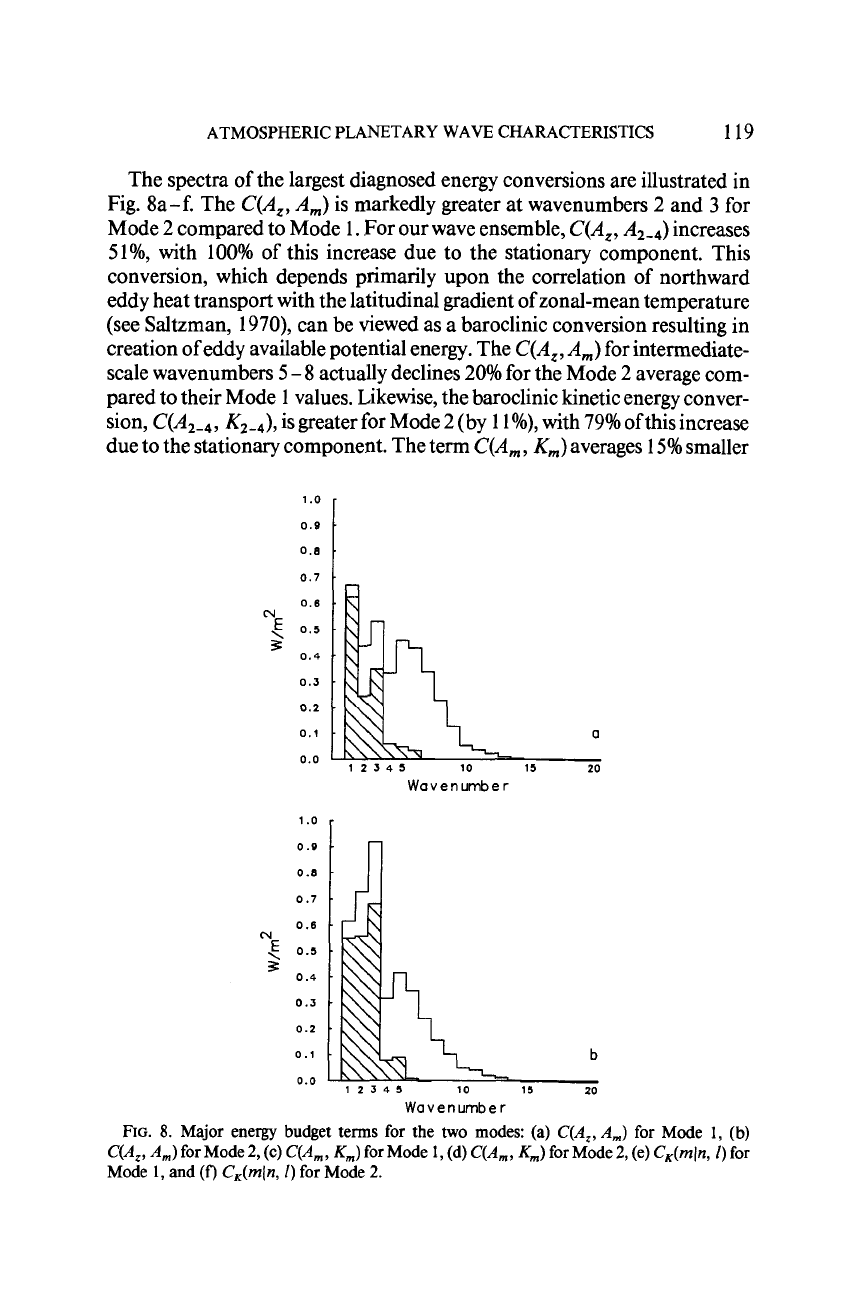
The spectra
of
the largest diagnosed energy conversions are illustrated in
Fig. 8a-f. The
C(A,,
A,)
is markedly greater at wavenumbers
2
and
3
for
Mode
2
compared to Mode
1.
For our wave ensemble,
C(A,,
A2-4)
increases
51%,
with
100%
of
this increase due to the stationary component. This
conversion, which depends primarily upon the correlation of northward
eddy heat transport with the latitudinal gradient of zonal-mean temperature
(see Saltzman,
1970),
can be viewed as a baroclinic conversion resulting in
creation of eddy available potential energy. The
C(A,,
A,)
for intermediate-
scale wavenumbers
5
-
8
actually declines
20%
for the Mode
2
average com-
pared to their Mode
1
values. Likewise, the baroclinic kinetic energy conver-
sion,
C(A2-4
,
K2-4),
is greater for Mode
2
(by
1
1%),
with
79%
of
this increase
due to the stationary component. The term
C(A,
,
K,)
averages
15%
smaller
0.6
N
E
0.5
0.4
Wavenumber
1
.o
0.9
0.8
0.7
0.6
N
E
0.5
0.4
0.3
0.2
0.1
0.0
Wavenumber
FIG.
8.
Major energy budget terms for the two modes: (a)
C(A,,A,)
for Mode
1,
(b)
C(A,,
A,)
for Mode
2,
(c)
C(A,,
K,)
for Mode
1,
(d)
C(A,,
K,)
for Mode
2,
(e)
C,(mln,
I)
for
Mode
1,
and
(f)
C,(mln,
I)
for Mode
2.
120
1.0
0.0
0.1
0.7
-
.
’
.
ANTHONY
R.
HANSEN
0.1
I::
0.0
lkL255-
20
12s45
10
15
Wavenlsnbe
r
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
12545
10
1s
20
Wave
n
unbe
r
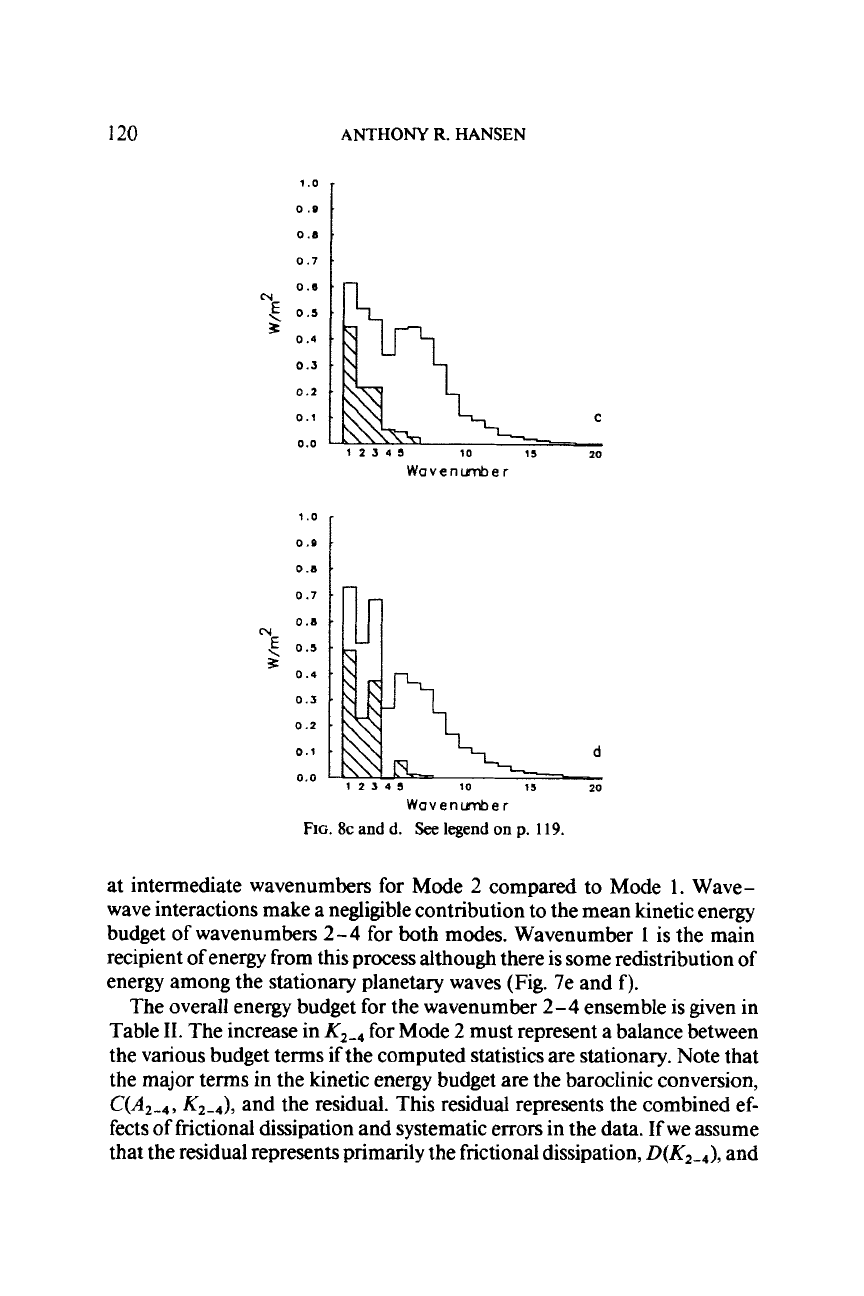
FIG.
8c and
d.
See
legend
on
p.
119.
at intermediate wavenumbers for Mode
2
compared to Mode
1.
Wave-
wave interactions make a negligible contribution to the mean kinetic energy
budget
of
wavenumbers
2
-
4
for both modes. Wavenumber
1
is the main
recipient of energy from this process although there is some redistribution of
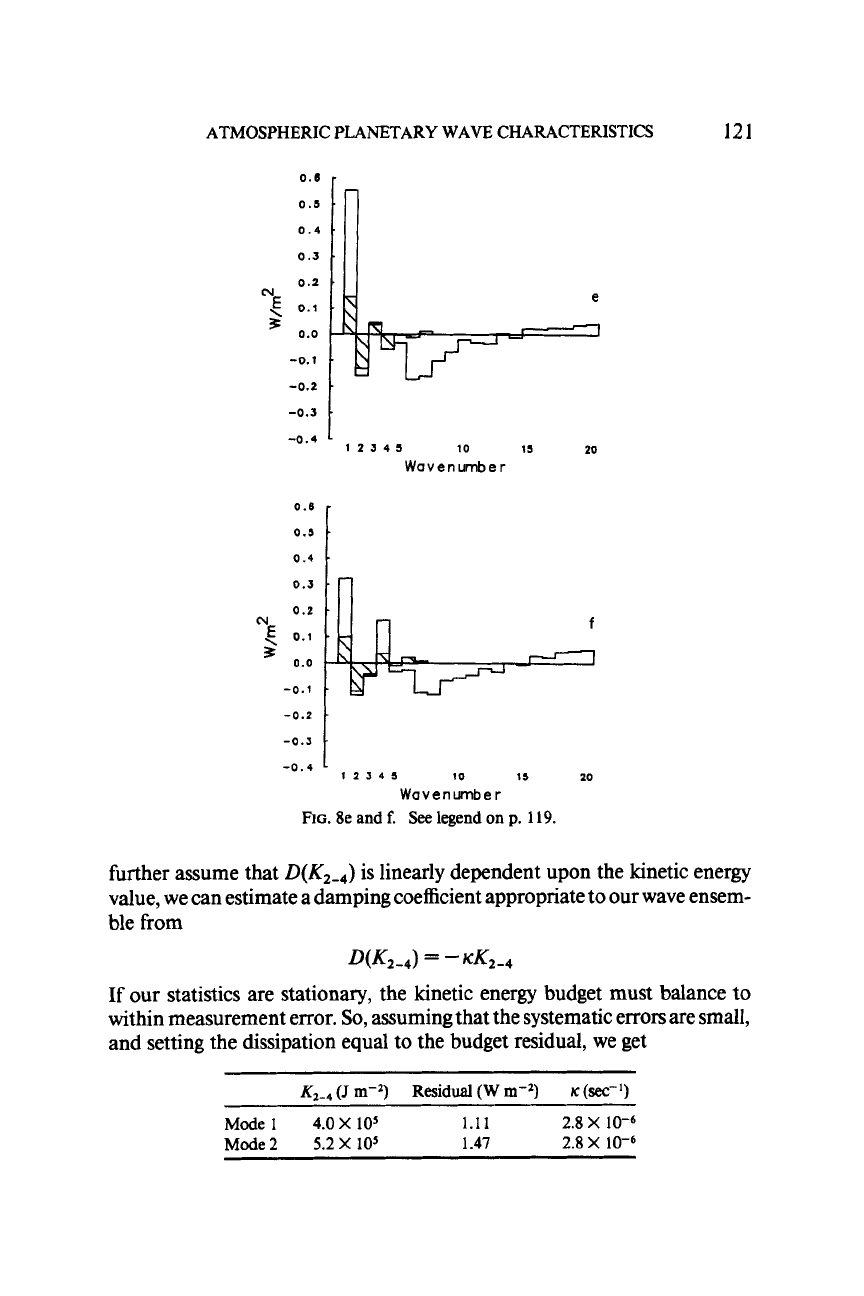
energy among the stationary planetary waves (Fig. 7e and f).
The overall energy budget for the wavenumber
2-4
ensemble is given in
Table
11.
The increase in
K2-4
for Mode
2
must represent a balance between
the various budget terms if the computed statistics are stationary. Note that
the major terms in the kinetic energy budget are the baroclinic conversion,
C(A,-,,
Kz-4),
and the residual. This residual represents the combined ef-
fects
of
frictional dissipation and systematic errors in the data.
If
we assume
that the residual represents primarily the frictional dissipation,
D(K2J,
and
ATMOSPHERIC PLANETARY WAVE CHARACTERISTICS
121
0.6
r
0.5
0.4
0.3
0.2
F(
0.7
0.0
-0.1
-0.2
e
12545
10
15
20
-0.4
-0*3
t
Wavenumber
hl
E
2
0.4
:::
1
0.3
0.2
0.1
0.0
-0.1
-0.2
1
Wave
n
umbe
r
FIG.
8e and
f.
See
legend on
p.
119.
further assume that
D(K2-,)
is linearly dependent upon the kinetic energy
value, we can estimate a damping coefficient appropriate to our wave ensem-
ble from
D(K2-4)
=
-xK2-4
If our statistics are stationary, the kinetic energy budget must balance to
within measurement error.
So,
assuming that the systematic errors are small,
and setting the dissipation equal to the budget residual, we get
Mode
1
4.0
X
los
1.11
2.8
X
Mode2
5.2X
los 1.41 2.8
X
I22
ANTHONY
R.
HANSEN
This value
of
K
=
2.8
X
sec-l corresponds to a momentum dissipation
time scale
T
=
2/~
of roughly
8
days.
The major source term in the
A2-4
budget is
C(A,,
A2-4)
with the sink
provided by
C(A,_,,
K2-J
leaving a small residual which represents data
inaccuracies as well as the generation term.
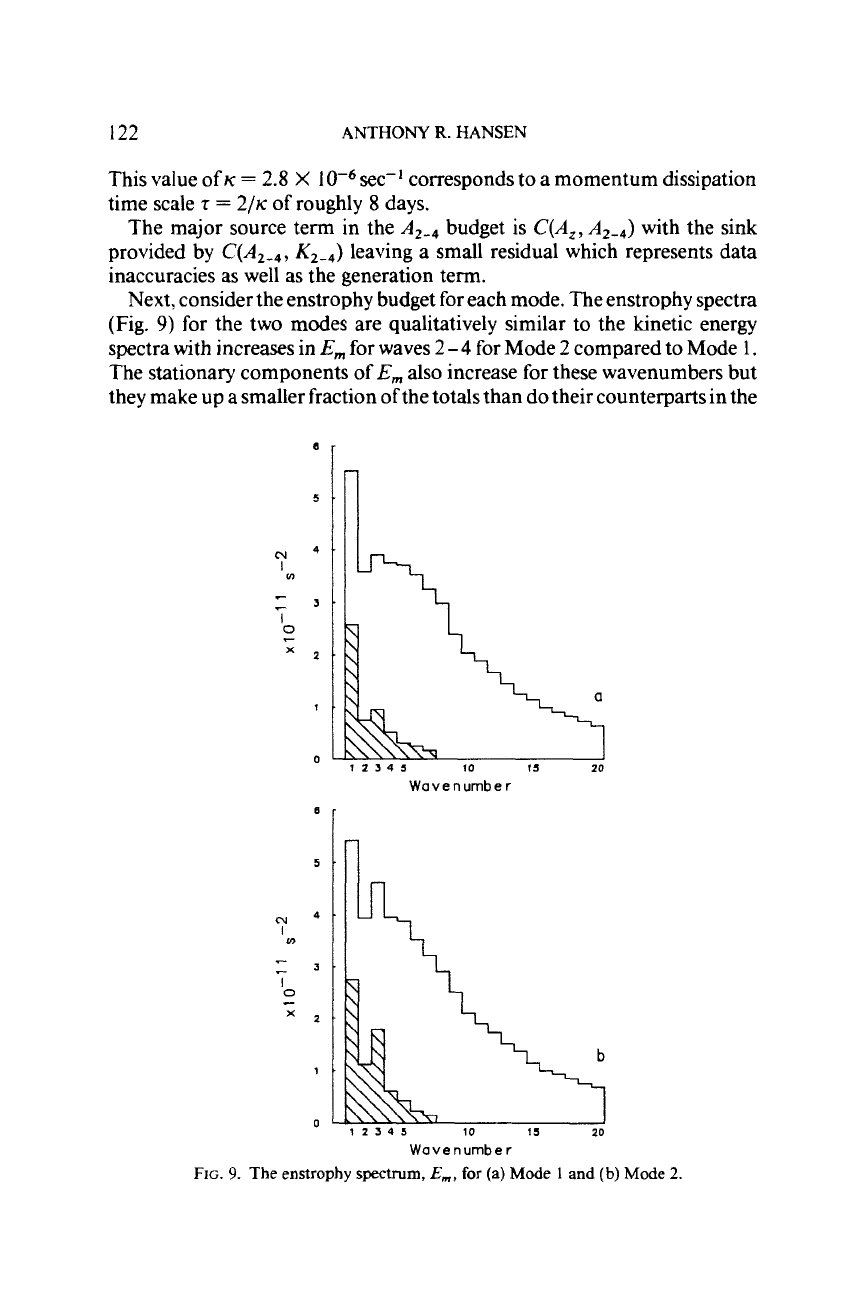
Next, consider the enstrophy budget for each mode. The enstrophy spectra
(Fig.
9)
for the two modes are qualitatively similar to the kinetic energy
spectra with increases in
Em
for waves
2
-
4
for Mode
2
compared to Mode
1.
The stationary components of
Em
also increase for these wavenumbers but
they make up a smaller fraction of the totals than do their counterparts in the
5
N4
Iv)
c
-3
I
0
?
x2
0
5
N4
‘m
Wavenumber
I
Wavenumber
12345
10
1s
20
Wavenumber
FIG.
9.
The
enstrophy
spectrum,
Em,
for
(a)
Mode
1
and
(b)
Mode
2.
ATMOSPHERIC PLANETARY WAVE CHARACTERISTICS
I23
1.4
1.3
1.2
1.1
energy spectra. Note that the
Em
spectrum is relatively steep for wave-
numbers
2
-
8
for Mode
2
compared to the flat spectrum of Mode
1
in this
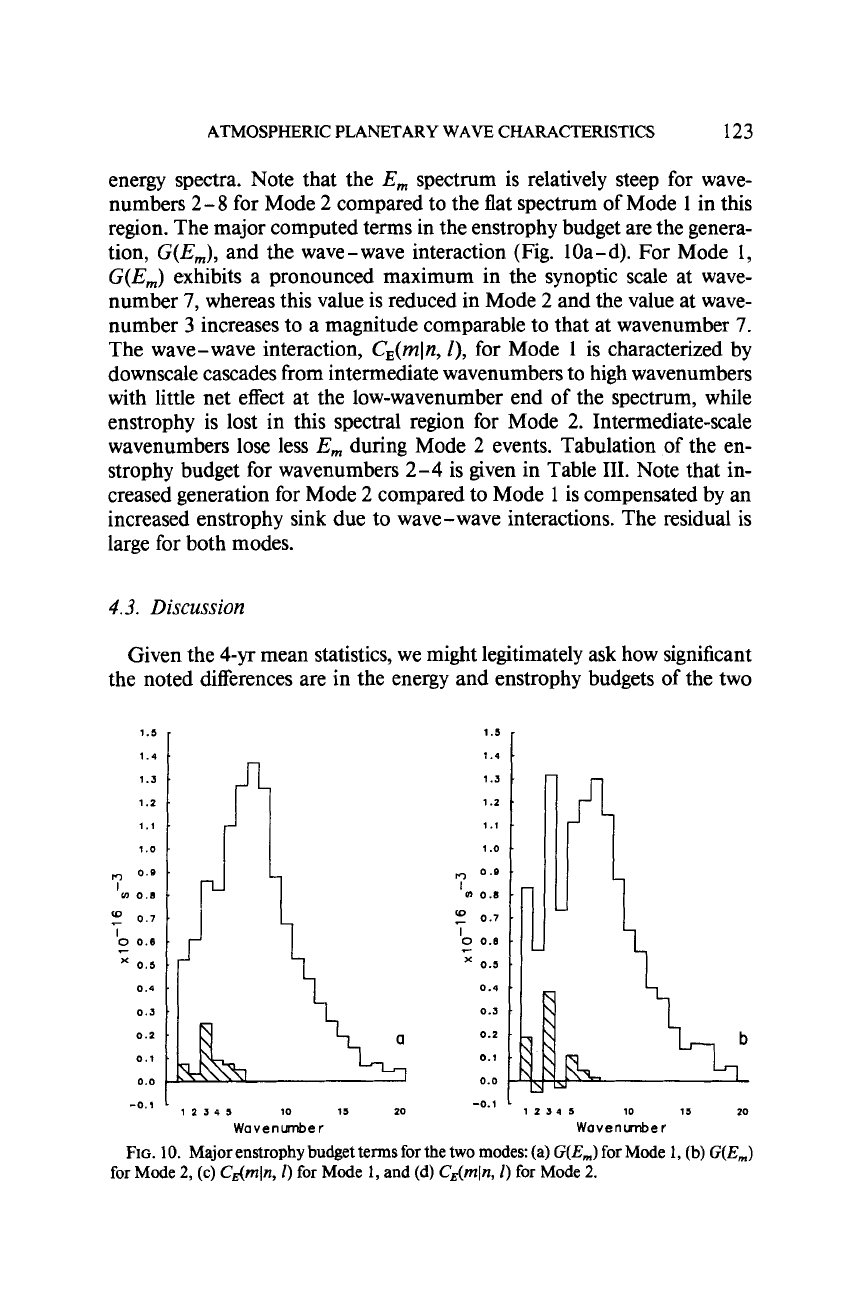
region. The major computed terms in the enstrophy budget are the genera-
tion,
G(Em), and the wave-wave interaction (Fig. 10a-d). For Mode l,
G(E,,,)
exhibits a pronounced maximum in the synoptic scale at wave-
number
7,
whereas this value
is
reduced in Mode
2
and the value at wave-
number
3
increases to a magnitude comparable
to
that at wavenumber
7.
The wave-wave interaction,
C,(mln,
I),
for Mode
1
is characterized by
downscale cascades from intermediate wavenumbers to high wavenumbers
with little net effect at the low-wavenumber end of the spectrum, while
enstrophy is lost in this spectral region for Mode
2.
Intermediate-scale
wavenumbers lose less
Em
during Mode
2
events. Tabulation of the en-
strophy budget for wavenumbers 2-4 is given in Table
111.
Note that in-
creased generation for Mode
2
compared to Mode
1
is compensated by an
increased enstrophy sink due to wave- wave interactions. The residual
is
large for both modes.
.
.
.
.
4.3.
Discussion
1.0
*
0.9
'*
0.8
b
0.8
0.7
v
0.5
0.4
0.3
0.2
0.1
0.0
Given the
4-yr
mean statistics, we might legitimately ask how significant
the noted differences are in the energy and enstrophy budgets of the two
'
.
.
.
.
'
'
.
.
.
-
1.5
1.4
1.3
1.2
1.1
1.0
*
0.9
'in
0.8
$
0.7
lo
0.6
7
0.5
0.4
0.3
0.2
0.1
0.0
I
12345 10
15
20
12345 10
15
20
-0.1
L
-0.1
Wave n
umbe
r
Wovenvnber
FIG.
10.
Major enstrophy budget terms
for
the two modes:
(a)
G(E,)
for
Mode
1,
(b)
G(E,)
for
Mode
2,
(c)
C,&n(n,
1)
for
Mode
1,
and (d)
CE(mIn,
I)
for
Mode
2.
