Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.


144
G.
J.
SHUTTS
force in the
i
direction
as
follows:
where
The conservative force may
be
combined with the pressure gradient term
so
that
Eqs.
(7)
and
(8)
may be reexpressed
as
1
a-
1-
]
:-
acos6
d3,
2
a-
a6
x
cos
$--(u’v’
cos2
$)
+-do’
+-
*
-(@
+
-vt2)=0
(9)
and
(approximated)
In effect, the important eddy forcing terms capable of generating mean
vorticity are “condensed” into a term representing a force in the east
-
west
direction. Conservative eddy forces, like the pressure gradient force, serve
only to balance the time-mean mass and wind fields.
The eddy forcing of zonal momentum
as
given by Eq.
(9)
can
be
written as
-
-
(Div
E
+
au’d
/dp)
with
E
=
[(p
-
u7)
cos
6,
-
u”
cos
61
in spherical polar geometry.
Hoskins
et
a/.
(
1983)
found that, typically, the high-pass filtered eddLfield
is elongated in the meridional direction corresponding to
v?
>
ut2
so
that
E
points eastward. “Bowing” of trough lines about the jetstream implies
a “fanning out” of the
E
vectors in the storm tracks with an equatorward bias
reflecting the dominance of poleward momentum transport in the zonal
mean.
Figure
3
shows the distribution of high-pass filtered
E
(using the same filter
as
Hoskins
et
al.,
1983)
at
300
mbar for the period
5
-
22
February. Two
regions
of
strong
eddy
momentum forcing
of
the block
are
evident.
Strong convergence of
E
into the jetstream split region implies decelera-
tion of westerlies there
of
the order of
10
msec-’/day while in the northern
jetstream branch, divergence of
E
implies acceleration
of
the flow. The
former region on the western side of the block agrees with the vorticity

A
CASE
STUDY
OF
EDDY
FORCING
145
forcing picture described earlier in which eddies propagating into a split
jetstream become extended meridionally, thereby tending to force an anti-
cyclonic/cyclonic dipole flow field. In contrast, the divergent
E
vectors at
65
ON
(near the Greenwich Meridian) are associated with baroclinic develop-
ment and have no counterpart in the aforementioned numerical experi-
ments.
The formation of depressions near Iceland and their subsequent intensifi-
cation over Scandinavia are quite commonly associated with Atlantic block-
ing ridges leading to strengthening of northerlies or northeasterlies over
western Europe.
Also
evident in Fig. 3 are westward-pointing
E
vectors
similar to those found by Hoskins
et
al.
(1983) in a case study of Atlantic
blocking though of weaker intensity.
5.
EDDY VORTICITY
FLUX
DIVERGENCE PATTERNS
Perhaps the most direct approach to quantifying the forcing effect of
eddies due to momentum transfer is to calculate the eddy vorticity flux
divergence and infer its effect from the mean vorticity equation. Large con-
servative forces disappear on taking the curl of the momentum equation,
though this is only at the expense
of
creating
a
more highly differentiated
(and therefore spatially detailed) diagnostic quantity. The point-by-point
variation
of
eddy vorticity flux divergence
is
of minor importance compared
to the overall pattern which determines the response in the large-scale pres-
sure field. Indeed, point values are likely to be inaccurate in view of the
numerical differentiation involved.
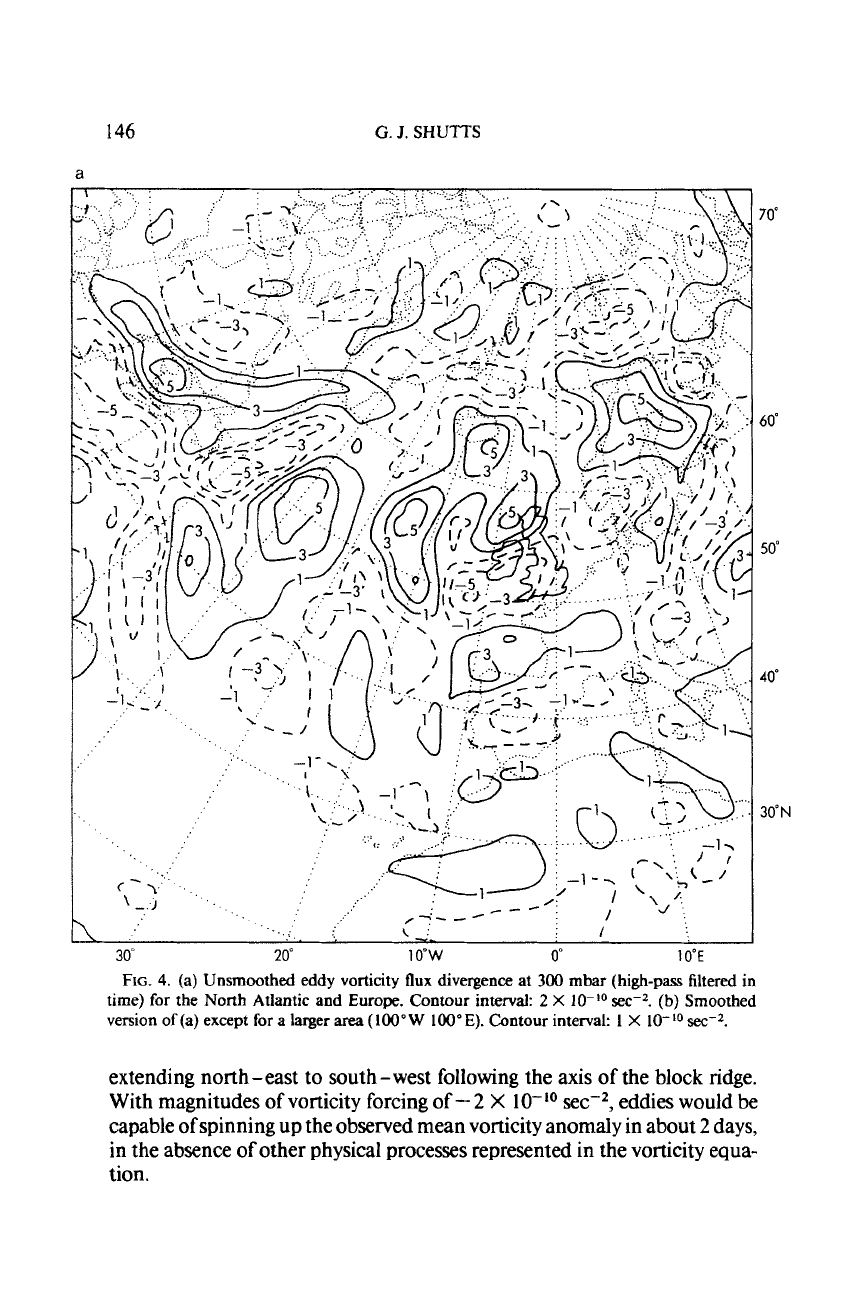
Figure 4a shows the eddy vorticity flux divergence at
300
mbar, for the
period with no spatial smoothing and high-pass filtered in time using the
method defined in Section 3. In spite of the rather complex pattern, individ-
ual features are quite well resolved since the horizontal spacing of gridpoints
is only 1.875
".
Anticyclonic forcing maxima appear at
50"
N
40"
W
just to
the north of the mean jetstream split, in the mean anticyclone near
20"
W
and over Scandinavia. Cyclonic forcing exists over much of Europe and to
some extent south of blocking anticyclone ridge in the Atlantic. Upstream of
the block the eddy vorticity flux divergence takes on a banded appearance
with some evidence of antisymmetry in the pattern about the jetstream axis.
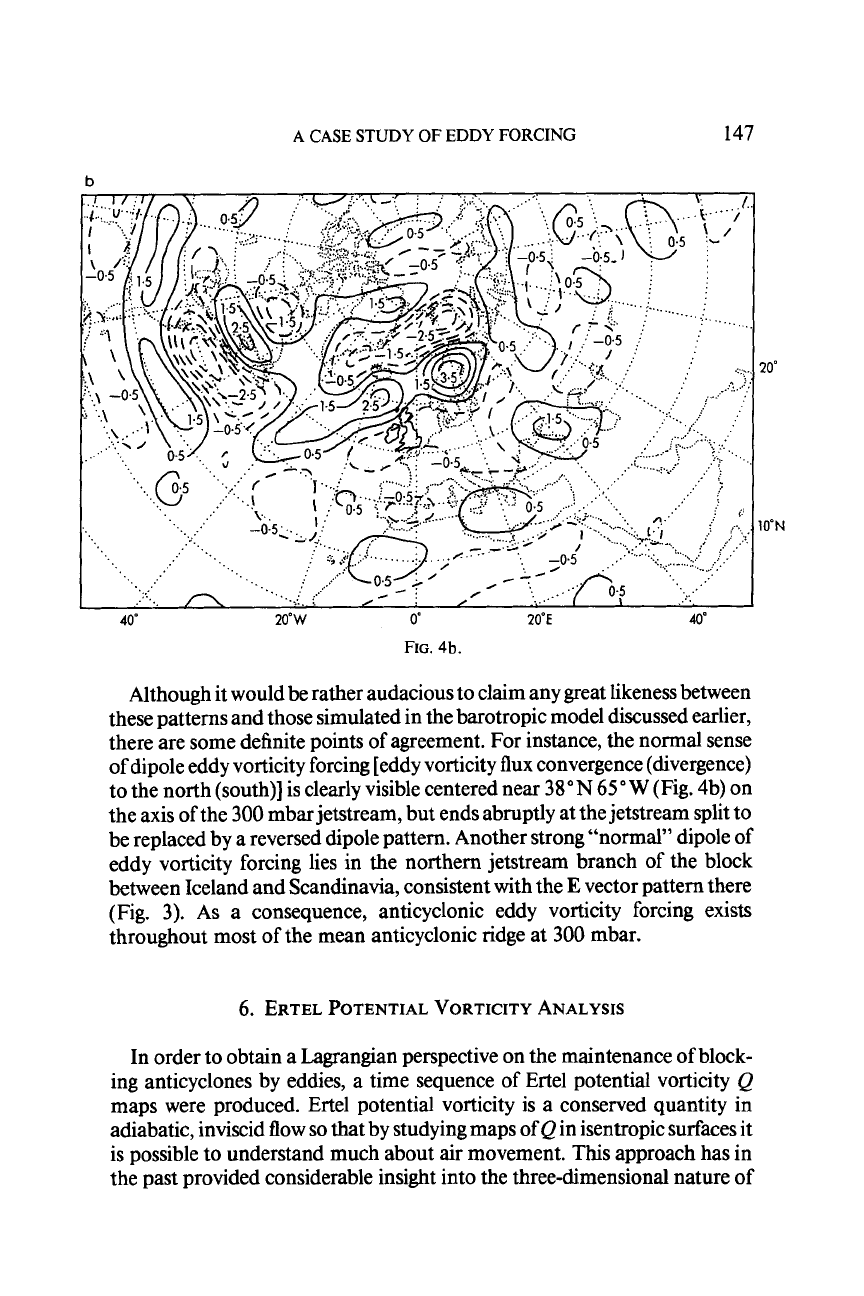
Spatial smoothing makes a tangible improvement to the ease of interpre-
tation of the eddy vorticity flux divergence fields. The smoothed version of
Fig. 4a (Fig. 4b) shows the dramatic change in eddy vorticity forcing charac-
teristics from the storm track pattern off the eastern seaboard of the United
States with a band of cyclonic forcing sandwiched between two bands of
anticyclonic forcing, to that in the blocking region with anticyclonic forcing
146
G.
J.
SHUTTS
a
extending north-east to south -west following the axis of the block ridge.
With magnitudes of vorticity forcing
of
-
2
X
sec-*, eddies would be
capable of spinning up the observed mean vorticity anomaly in about
2
days,
in the absence of other physical processes represented in the vorticity equa-
tion.
A CASE STUDY OF EDDY FORCING
147
b
FIG.
4b.
Although it would be rather audacious to claim any great likeness between
these patterns and those simulated in the barotropic model discussed earlier,
there are some definite points
of agreement. For instance, the normal sense
of dipole eddy vorticity forcing [eddy vorticity flux convergence (divergence)
to the north (south)] is clearly visible centered near
38"
N
65
OW
(Fig. 4b) on
the axis
of
the
300
mbar jetstream, but ends abruptly at the jetstream split to
be replaced by a reversed dipole pattern. Another strong "normal" dipole of
eddy vorticity forcing lies in the northern jetstream branch of the block
between Iceland and Scandinavia, consistent with the
E
vector pattern there
(Fig.
3).
As
a consequence, anticyclonic eddy vorticity forcing exists
throughout most of the mean anticyclonic ridge at
300
mbar.
6.
ERTEL POTENTIAL VORTICITY ANALYSIS
In order
to
obtain a Lagrangan perspective on the maintenance of block-
ing anticyclones by eddies, a time sequence of Ertel potential vorticity
Q
maps were produced. Ertel potential vorticity is a conserved quantity in
adiabatic, inviscid flow
so
that by studying maps of
Q
in isentropic surfaces it
is possible to understand much about air movement.
This
approach has in
the past provided considerable insight into the three-dimensional nature of

148
G.
J.
SHUTTS
cyclone-wave development, frontogenesis, and the associated exchange of
chemical tracers between troposphere and stratosphere (Reed,
1955;
Dan-
ielsen,
1968).
Recently McIntyre and Palmer
(1983)
have advocated isen-
tropic analysis of
Q
to reveal Rossby wave breaking processes in the upper
subtropical troposphere, similar to those found in sudden warming events in
the stratosphere. The eddy enstrophy cascade mechanism
discussed
in Sec-
tion
2
can also
be
regarded
as
a wave breaking process in which the east
-
west
scale of eddies collapses and
Q
is irreversibly mixed.
In an exhaustive review of the concept of Ertel potential vorticity, Hoskins
ei
al.
(1985)
show that this single quantity and its behavior in isentropic
surfaces provide a physical basis, at least conceptually, for unifying our
understanding of most large-scale dynamical phenomena in meteorology
(e.g., baroclinic instability, Rossby wave propagation, and frontogenesis)
when a suitably defined notion of balance exists. They argue that isentropic
Q
maps are the key to sharpening our dynamical insight into the full-three
dimensional structure of real atmospheric motion systems and present ex-
amples of the formation and maintenance of cut-off lows and blocking
anticyclones using such an analysis technique. On a more cautionary note, if
we accept that systems of equations incorporating a level of balance higher
than quasi-geostrophy permit discontinuous behavior, then the potential
vorticity approach may
be
undermined. In these cases the Lagrangian con-
servation
of
more fundamental physical quantities such as gas entropy and
momentum are required (Cullen,
1983;
Cullen and Purser,
1984).
These
objections are unlikely, however, to detract from the usefulness of isentropic
Q
maps for observational purposes.
The isentropic coordinate expression for Ertel potential vorticity adopted
here is
Q
=
-(L
+f)
*
(1/8Hde/d~)
where
re
is the relative vorticity of the horizontal wind vector and
(l/8)
d8/dp)
is
the static stability both measured on a chosen isentropic surface.
Temperature fields at
850,700,500,400,300,250,200,
and
150
mbar are
converted to potential temperature and interpolated using a cubic spline
fitting procedure to find
p.,
the pressure corresponding to the level of the
isentropic surface
8..
The vertical profile of potential temperature for each
gridpoint is then represented by a fifth-order polynomial in pressure and
differentiated for the static stability at
p..
The wind components are interpo-
lated to the isentropic surface and
lo
is found by the standard centered-dif-
ference expression for curl.
Vertical interpolation for
p.
is
sensitive to the nature of the
8
profile, and
the cubic splines routine often
fails
if an isentropic layer is detected. In these
cases, linear interpolation
is
used to find
p..
Unfortunately, isentropic layers
A CASE
STUDY
OF
EDDY FORCING
I49
are quite common beneath the tropopause and near the surface over sub-
tropical deserts. Superadiabatic layers are sometimes found in the European
Centre for Medium Range Weather Forecasts archived temperature data and
arise from the interpolation of model fields from sigma to pressure levels
(A.
Hollingsworth, 1983; personal communication). Isentropic and superadia-
batic layers were adjusted to make
(-dB/dp)
small and positive
so
as to
provide a monotonically increasing sequence
of
6
values for the interpola-
tion routine.
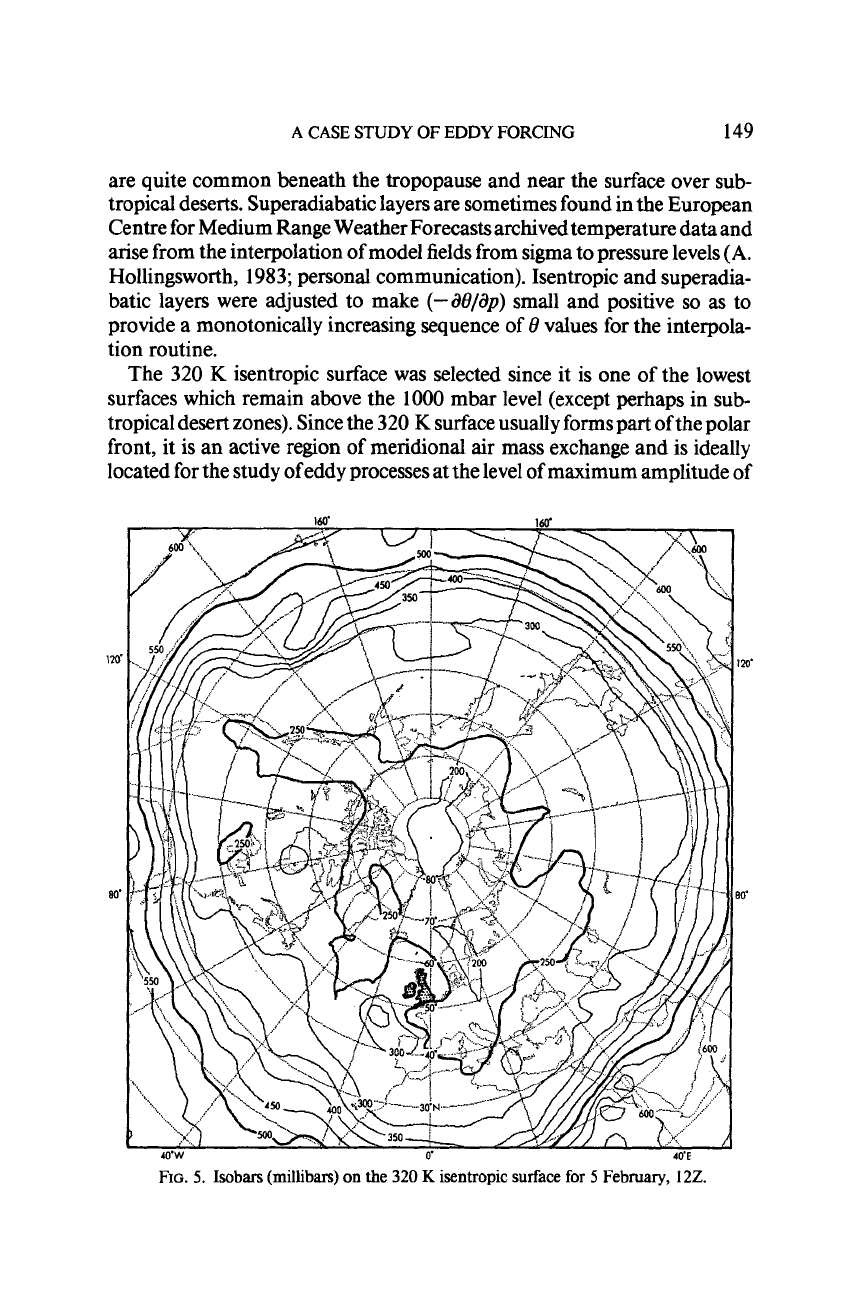
The
320
K
isentropic surface was selected since it is one of the lowest
surfaces which remain above the
1000
mbar level (except perhaps in sub-
tropical desert zones). Since the
320
K
surface usually forms part of the polar
front, it is an active region of meridional air mass exchange and is ideally
located for the study ofeddy processes at the level of maximum amplitude of
FIG.
5.
Isobars
(milliban)
on
the
320
K
isentropic surface for
5
February,
122.
150
G.
J.
SHUTTS
the block (about
300
mbar). On average it
slopes
from
200
mbar over the
pole to
600
mbar in the tropics. Figure
5
shows isobars of the
320
K
surface
on the first day of the
period.
In middle and high latitudes the
320
K
surface
is sufficiently high for nonconservative effects associated with latent heat
release in condensation of water vapor to
be
unimportant.
Gradients of
Q
become very large where the surface intersects the tropo-
pause and enters the lower stratosphere. For the purposes of display, the
fourth root
of
Q
is plotted
so
as
to give more emphasis to gradients in the
subtropics and middle latitudes. It goeswithout saying that any function of
Q
is conserved following the motion of a parcel if
Q
is conserved. The rather
arbitrary choice of this function here highlights the possibility that there
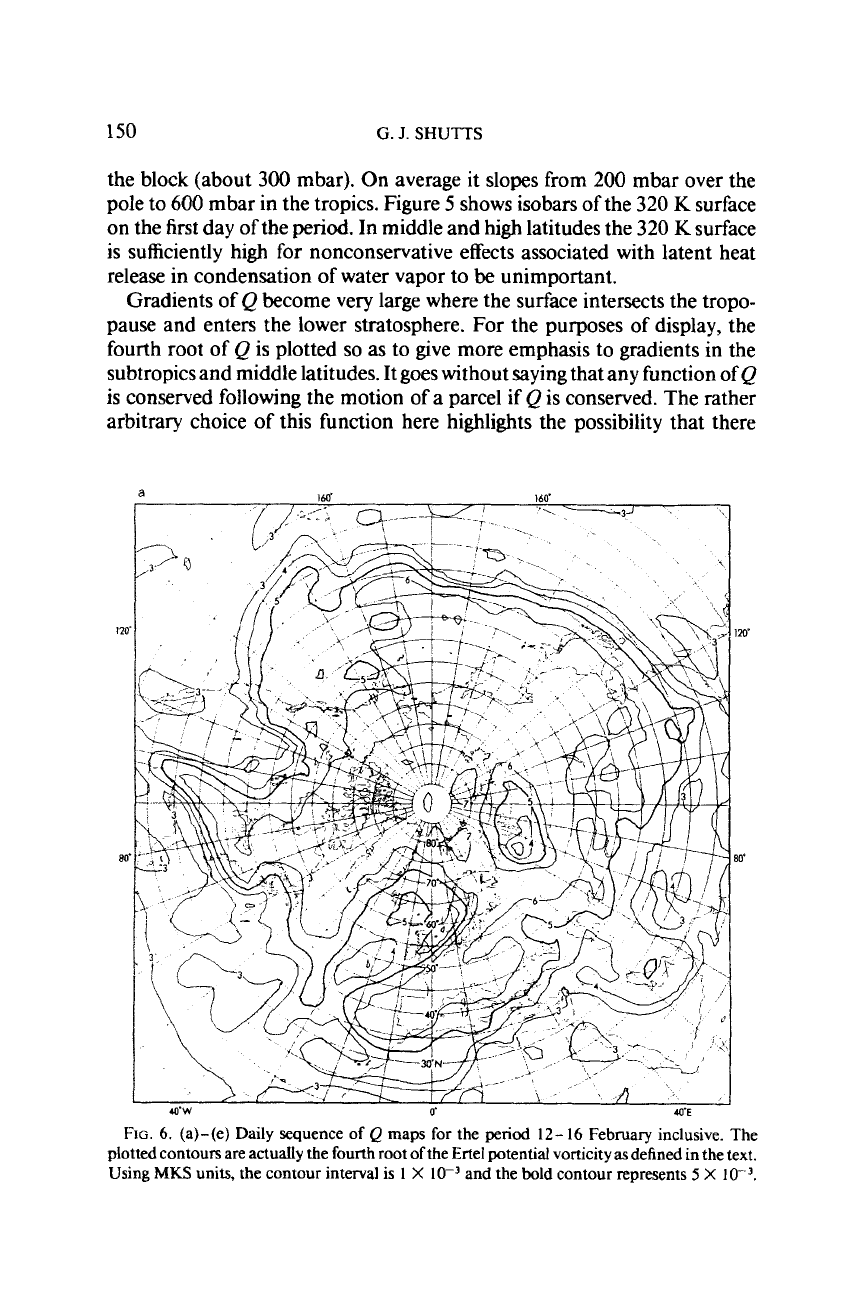
FIG.
6.
(a)-(e) Daily sequence of
Q
maps for the
period
12-
16
February inclusive. The
plotted
contours
are actuaUy the fourth root ofthe Ertel potential vorticityas defined
in
the text.
Using
MKS
units, the
contour
interval is
1
X
lW3
and the
bold
contour represents
5
X
lo-’.

A CASE STUDY
OF
EDDY
FORCING
151
exists some optimal functional form. B.
J.
Hoskins
(1983;
personal commu-
nication) has suggested that might be a useful choice since the diabatic
source term in the isentropic equation for
Q-'
can be written in a flux form,
(d/dp)(H/Q),
where His the diabatic heating. For the period
5
-
22
February
Q
maps have been produced four times daily, though only five are repro-
duced here.
A
twice-daily selection is to be collated as a Meteorological
Office Technical Note available on request.
Figures 6a
-
6e are a sequence
of
maps of
Q
lf4
(hereafter we shall refer to
Q
as
Q)
at
122
for
I2
-
16 February inclusive during which time a major
injection
of
low
Q
into the block occurs.
The first
Q
map shows the blocking anticyclone as
a
region of low
Q
to
the
west of the British Isles and extending northward to Iceland. Lowest
Q
values
occur in a band along the eastern flank of the region from southern Norway
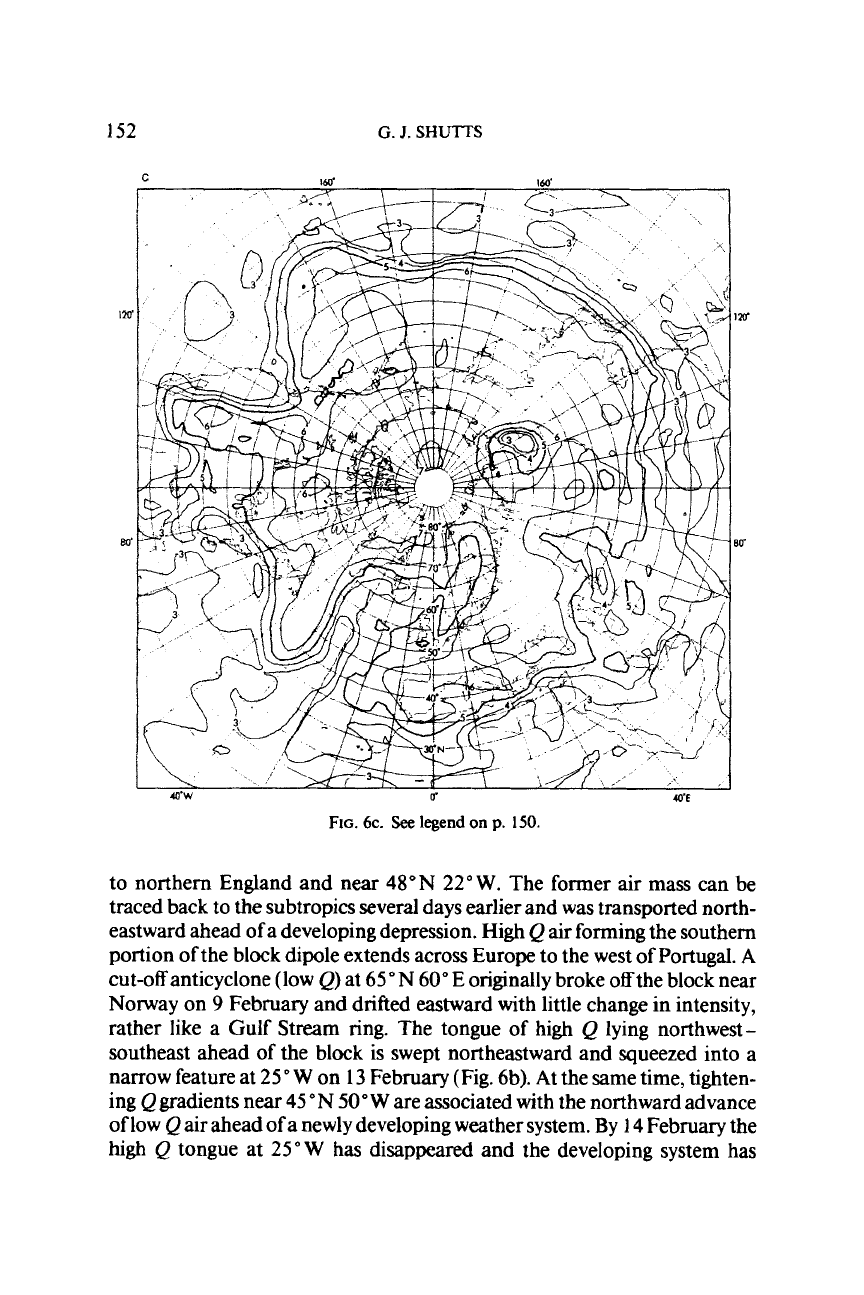
FIG.
6b.
152
G.
J.
SHUTTS
FIG.
6c.
See
legend
on
p.
150.
to northern England and near 48"N
22"
W.
The former air mass can be
traced back to the subtropics several days earlier and was transported north-
eastward ahead
of
a developing depression. High Q air forming the southern
portion of the block dipole extends across Europe to the west of Portugal.
A
cut-off anticyclone (low Q) at
65"
N
60"
E
originally broke
off
the block near
Norway on
9
February and drifted eastward with little change in intensity,
rather like a Gulf Stream ring. The tongue
of
high Q lying northwest-
southeast ahead
of
the block is swept northeastward and squeezed into a
narrow feature at
25
OW
on
13
February (Fig. 6b). At the same time, tighten-
ing Qgradients near 45"N
50"W
are associated with the northward advance
of low Q air ahead of a newly developing weather system. By 14 February the
high
Q
tongue at
25"
W
has disappeared and the developing system has
A
CASE
STUDY
OF
EDDY
FORCING
153
FIG.
6d.
See
legend on
p.
150.
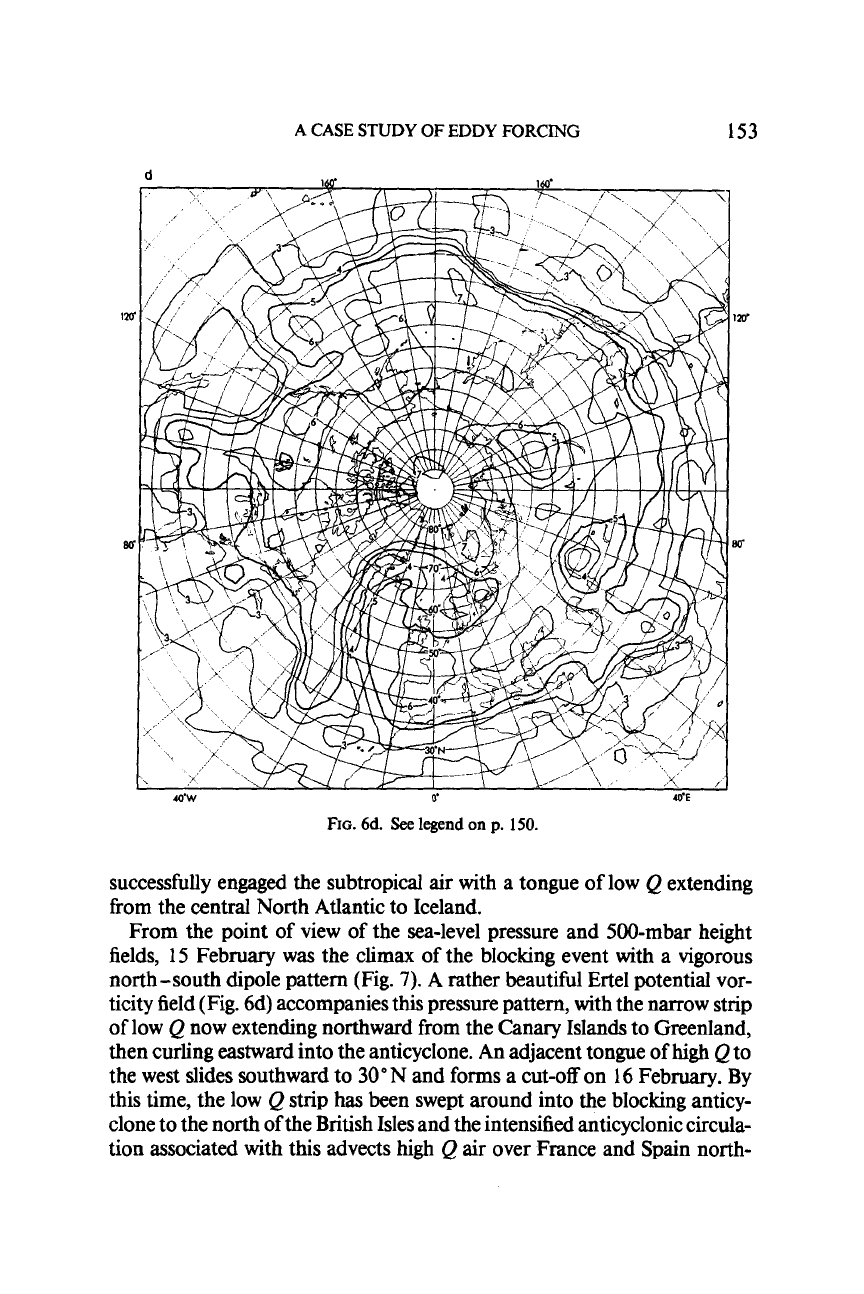
successfully engaged the subtropical air with a tongue of low
Q
extending
from the central North Atlantic to Iceland.
From the point of view of the sea-level pressure and 500-mbar height
fields,
15
February
was
the climax of the blocking event with
a
vigorous
north -south dipole pattern (Fig.
7).
A
rather beautiful Ertel potential vor-
ticity field (Fig. 6d) accompanies this pressure pattern, with the narrow strip
of low
Q
now extending northward from the Canary Islands to Greenland,
then curling eastward into the anticyclone. An adjacent tongue of
high
Q
to
the west slides southward to
30"
N and forms a cut-off on
16
February. By
this time, the low
Q
strip has been swept around into the blocking anticy-
clone to the north of the British Isles and the intensified anticyclonic circula-
tion associated with this advects high
Q
air
over France and Spain north-
