Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.


This Page Intentionally Left Blank

THE EFFECT OF LOCAL BAROCLINIC
INSTABILITY ON ZONAL
INHOMOGENEITIES OF VORTICITY AND
TEMPERATURE
R. T.
PIERREHUMBERT
Geophysical Fluid Dynamics Laboratory
National Oceanic and Atmospheric Administration
Princeton University
Princeton,
New
Jersey
08542
1.
INTRODUCTION
The central problem in the theory of persistent anomalies in the atmo-
sphere is to account for the magnitude of high-amplitude anomalies and for
the persistence of such amplitudes. Any attack on the problem is immedi-
ately faced with the existence of a vigorous spectrum of transient synoptic-
scale baroclinic eddies; there are no observations which suggest that such
eddies disappear during blocking episodes. It is therefore ofgreat importance
to understand the effects of synoptic eddies on the large-scale environment
through which they propagate. This is equally true whether one thinks of the
anomalies as resulting from strongly nonlinear processes -as in the various
multiple-equilibria theories
-
or from essentially linear free and forced
Rossby waves. The nature
of
the eddy effects is also relevant to the theory
of
the structure
of
the climatological stationary waves and of the associated
storm tracks.
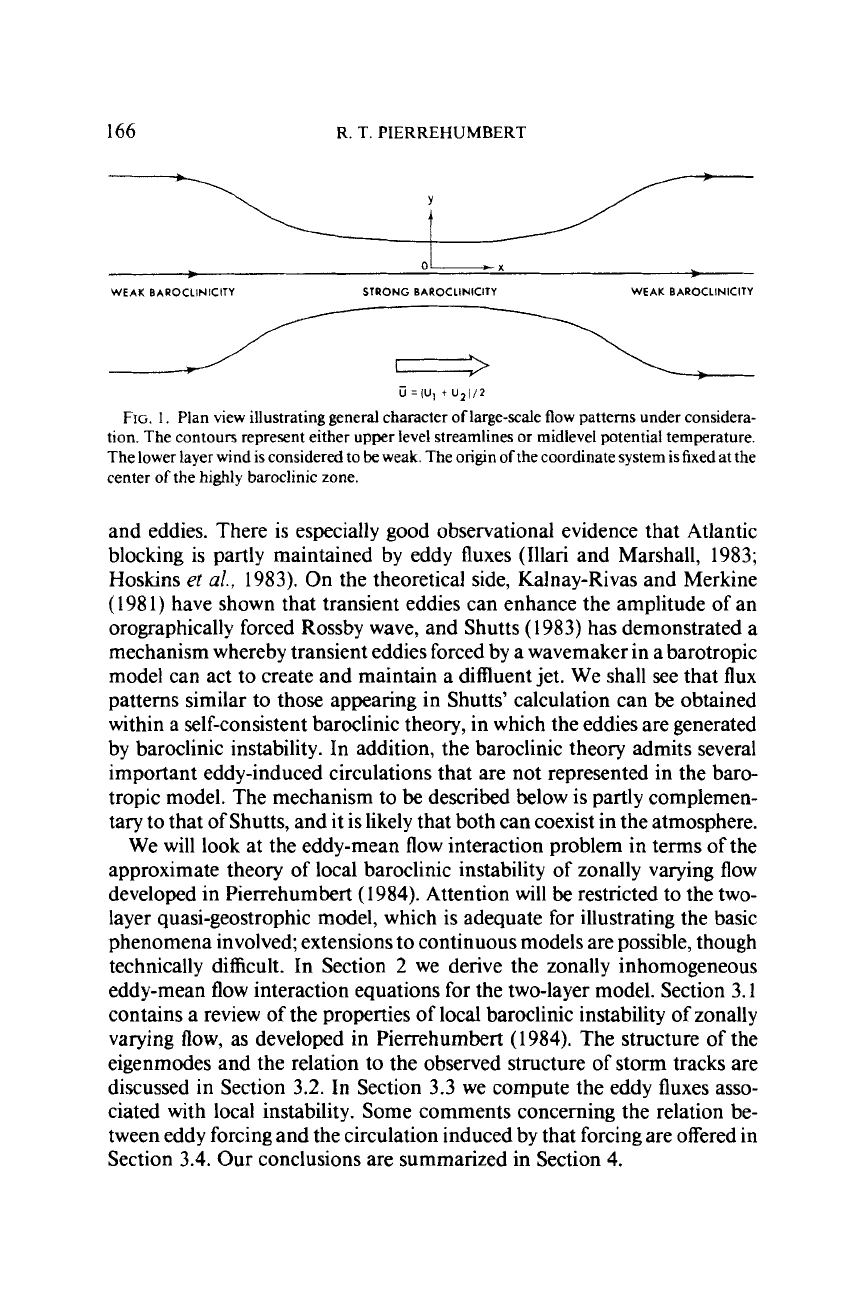
Generally speaking, we shall be concerned with the feedback of eddies on a
large-scale diffluentjet pattern consisting of a region ofweak winds and weak
baroclinicity downstream of a zone of intense winds and baroclinicity, such
as pictured in Fig.
1.
Since the synoptic eddies draw their energy from the
meridional temperature gradient, it is expected that mixing
of
this gradient
will occur in response. The fundamental question is whether the mixing
occurs predominantly in the highly baroclinic zone, where it would tend to
destroy the large-scale pattern, or downstream of the baroclinic zone, where
it would tend to accentuate the zonal inhomogeneity. Vorticity fluxes gener-
ated as
a
byproduct of the eddy evolution may also
act
to maintain or destroy
the basic state.
The two Northern Hemisphere blocking regions are at the end
of
the
climatological storm tracks, hinting at a direct connection between blocking
165
Copyright
0
1986
by
Academic
Resr,
Inc.
All
rights
of
reproduction
in any
form
resewed.
ADVANCES
IN
GEOPHYSICS,
VOLUME
29
166
R.
T.
PIERREHUMBERT
-
OLX
r
I
WEAK BAROCLINICITY STRONG BAROCLINICITY WEAK BAROCLINICITY
r
0
=iu,
t
u21/2
FIG.
1.
Plan view illustrating general character
of
large-scale
flow
patterns under considera-
tion. The contours represent either upper level streamlines
or
midlevel potential temperature.
The lower layer wind is considered to
be
weak. The
origin
ofthe coordinate system
is
fixed at the
center
of
the highly baroclinic zone.
and eddies. There is especially good observational evidence that Atlantic
blocking is partly maintained by eddy fluxes (Illari and Marshall,
1983;
Hosluns
et
al.,
1983).
On
the theoretical side, Kalnay-Rivas and Merkine
(198
1)
have shown that transient eddies can enhance the amplitude of an
orographically forced Rossby wave, and Shutts
(
1983)
has demonstrated a
mechanism whereby transient eddies forced by a wavemaker in a barotropic
model can act to create and maintain a diffluent jet. We shall see that flux
patterns similar to those appearing in Shutts’ calculation can be obtained
within
a
self-consistent baroclinic theory, in which the eddies are generated
by baroclinic instability. In addition, the baroclinic theory admits several
important eddy-induced circulations that are not represented in the baro-
tropic model. The mechanism to be described below is partly complemen-
tary to that of Shutts, and it is likely that both can coexist in the atmosphere.
We will look at the eddy-mean flow interaction problem in terms of the
approximate theory of local baroclinic instability of zonally varying flow
developed in Pierrehumbert
(1
984).
Attention will be restricted to the two-
layer quasi-geostrophic model, which is adequate for illustrating the basic
phenomena involved; extensions to continuous models are possible, though
technically difficult. In Section
2
we derive the zonally inhomogeneous
eddy-mean flow interaction equations for the two-layer model. Section
3.1
contains a review of the properties of local baroclinic instability of zonally
varying flow, as developed in Pierrehumbert
(1
984).
The structure of the
eigenmodes and the relation to the observed structure of storm tracks are
discussed in Section
3.2.
In
Section
3.3
we compute the eddy fluxes asso-
ciated with local instability. Some comments concerning the relation be-
tween eddy forcing and the circulation induced by that forcing are offered in
Section
3.4.
Our conclusions are summarized in Section
4.

THE
EFFECT
OF
LOCAL BAROCLINIC INSTABILITY
167
2.
EDDY
FLUXES
IN
THE
TWO-LAYER
MODEL
Consider quasi-geostrophic flow
of
two layers
of
fluid of depth
f),
denoting
upper layer quantities with the subscript
1
and lower layer quantities with the
subscript
2.
In nondimensional units with velocity scale Uand length scale
LD
=
[gDSp/(pof2)]’/2,
the equations of motion are
(1)
(2)
In Eq.
(2)
yjis the streamfunction and
P
=
P&Lb/U.
The term
Rj
in Eq.
(1)
represents the net forcing and dissipation. Next consider an ensemble of
solutions to Eq.
(
l),
denoting the average of a quantity
A
over this ensemble
by
(A)
and the deviation from the average by
A’.
Then, the ensemble average
tendency is
(3)
Suppose now that
(Rj)
exactly balances the mean advection,
so
that the term
in curly brackets vanishes. This amounts to the assumption that the ensem-
ble average state is a steady state in the absence of the eddies. Under this
condition, the first term on the right-hand side gives the
initial
vorticity
tendency that would result from perturbing the steady state with an ensem-
ble of eddies. Given the potential vorticity tendencies, one can easily solve
for the geopotential height and temperature tendencies. Initial tendency
calculations have proven useful in diagnosing transient eddy effects in the
real atmosphere (Lau and Holopainen,
1984;
Hoskins
et
al.,
1983)
and
therefore serve as a convenient vehicle for comparison between theory and
observation. However, one must be aware that the initial tendencies do not
represent the ultimate effect of the eddies on the mean flow. We shall return
to this point in Section
3.4.
The interpretation
of
the tendency is simplified by splitting it into a baro-
tropic and a baroclinic part. To obtain the former, we add the upper and
lower layer equations, resulting in
at%
=
-v
-
F
(44
(4b)
+
((v’,Vzv{
+
v$V2y$))ey
(4c)
a,qj
+
v
-
vjqj
=
R~
qj
=
VzYj
+
(-
1)Y~l-
YZ)
+
PY
where the potential vorticity is
at(qj)
=
-V
*
(vjqj)
+
{(Rj)--V
*
(vj)(qj))
where
qB
=
(v2(y/,
+
y2))
F
=
((u;V2y;
-+
u;V2&))ex

I68
R.
T.
PIERREHUMBERT
and
ex
and
ey
are the unit vectors in the zonal and meridional direction. The
vector
F
is simply the vertically integrated horizontal flux of relative vortic-
ity, and
Eq.
(4a) states that the initial rate of change of vertically integrated
relative vorticity is opposite to the divergence of the integrated relative
vorticity flux.
The baroclinic structure
of
the tendency is obtained by subtracting the
lower layer tendency from the upper layer tendency. We obtain
aiqT
=
--(v
-
G
-
v
-
H)
qT
=
v2((w1
-
w2))
-
((wl
-
w2))
(5a)
(5b)
+
(u;V2v/;
-
u;V2y/;)ey
(5c)
where
G
=
(u;02yY;
-
u;V2t&)ex
According to
Eq.
(5b), the streamfunction of the thermal wind can
be
recov-
ered from
qT
by solving a linear elliptic equation; because ofthe minus sign in
the second term on the right-hand side of Eq.
(5b),
the Greens’ function of
the problem is exponentially decaying, with characteristic length equal to the
radius
of
deformation. The tendency of
qT
has contributions from the diver-
gence of
G
and
H;
G is the difference in the relative vorticity fluxes in the two
layers while
H
is twice the horizontal heat flux. The contribution
of
the
vorticity flux to the thermal wind arises because the flux sets up mean
circulations which create dynamic heating via mean vertical motions. The
necessity
of
solving an elliptic equation to find the thermal wind (even in the
absence of
G)
arises because heat and vorticity fluxes create mean circula-
tions which affect the winds via the Coriolis force. When the spatial scale of
the ensemble-averaged fluxes is large compared to the radius of deformation,
Eq.
(5a) reduces to
(6)
a,(w,
-
wz)
=
v
-
G
-
v
-
H
which gives the temperature tendency (and hence thermal wind tendency) in
terms of the divergence of heat and vorticity fluxes. The G is not
a
priori
negligible compared to
H,
as
the eddies themselves could have scales compa-
rable to the radius of deformation even when the associated rectified fluxes
vary slowly in space. However, we shall
see
that in theory as in observation,
the synoptic eddies have a vertical structure such that the first term in the
right-hand side of
Eq.
(6)
is negligible, whence the temperature tendency is
approximately proportional to the heat
flux
convergence.

THE EFFECT
OF
LOCAL BAROCLINIC INSTABILITY
169
3.
FLUXES
AND
TENDENCIES ASSOCIATED
WITH
LOCAL BAROCLINIC
INSTABILITY
3.1.
Summary
of
Properties
of
Local Baroclinic Instability
We will attack the problem of eddy-anomaly feedback by computing the
pattern of eddy fluxes associated with the most unstable baroclinic eigen-
mode occuring in the system linearized about the given zonally inhomoge-
neous flow. The results will be used in an attempt to determine whether the
eddies act to maintain or destroy the deviations of the basic state from its
zonal mean. This approach suffers from two deficiencies:
(1)
the fluxes
during the transient stage before the eigenmode emerges are ignored, and
(2)
changes in the character of the eddies arising from the nonlinear process
of
maturation and decay are neglected. Of course, linear theory gives no infor-
mation on the overall magnitude of the fluxes. Nevertheless,
it
is of interest
to see how far we can get in explaining the qualitative aspects of the observa-
tions with linear theory alone, in the hope that discrepancies may bring into
relief the kinds of nonlinear effects that are most important.
Instead of dealing with the exact zonally inhomogeneous stability prob-
lem, we will make use of the approximate theory developed in Pierrehum-
bert
(
1984),
the rudiments ofwhich we will outline here. This theory relies on
a separation in scale between the size of the eddies and the scale
of
variation
of
the basic state; although it was developed within the framework of the
two-layer quasi-geostrophic model without meridional shear, generaliza-
tions are possible. Let
U,(x)
be the upper layer basic-state wind,
U,(x)
be the
lower level wind,
Urn
=
(U,
+
U2)/2,
and
DU
=
(U,
-
U2).
Further, assume
that the maximum shear occurs at
x=O
and is normalized such that
DU(0)
=
1;
let the minimum shear occumng downstream of the highly
baroclinic zone be denoted by
DU,,
.
This situation is depicted in Fig.
1.
The
key to understanding the instability of such flows is the concept
of
“absolute
growth rate.” For zonally independent flows in a domain of infinite zonal
extent, the absolute growth rate is the growth rate observed at a fixed point in
space (as opposed to moving along with the unstable wave packet). The
absolute growth rate can be obtained from the conventional dispersion rela-
tion; it is always less than or equal to the familiar maximum normal mode
growth rate and generally decreases monotonically when
Urn
is increased
while holding
DU
fixed. For a fuller exposition, see Pierrehumbert
(1984),
wherein the following results concerning local instability were obtained.
Local modes, which are defined
as
eigenmodes that decay to zero at large
1x1,
exist provided two conditions are met:
(1)
the flow must
be
absolutely unsta-
ble at the point of maximum baroclinicity, and
(2)
DU,,
must be less than a
certain critical value which depends on
j3
and the pattern
of
U,,,
.
When local

170
R.
T.
PIERREHUMBERT
modes exist. their growth rates are equal to the absolute growth rate evalu-
ated at the point of maximum baroclinicity. Since absolute growth rate falls
to
zero for sufficiently large
Urn,
it is not difficult to stabilize the flow against
absolute baroclinic instability in physically plausible circumstances; in such
a flow, all unstable disturbances eventually propagate away leaving nothing
behind. Thus, when a flow is absolutely stable, eddies may propagate away
before they have time to affect the anomaly. The peak amplitude of a local
eigenmode occurs downstream
of
the site of maximum baroclinicity, and the
downstream shift increases with increasing
Urn.
For
x
>
0,
a local eigenmode has the
WKB
form
v;
=
AJ(x)[A(x)em]
cOs('p) (74
where
A(x)
=
exp[
-
(
[kidx)]
exp(o,t)
and
cy
=
[k,&
-
w,t
The complex zonal wavenumber
k(
U,(x), U,(x),
w)
is determined by solv-
ing the familiar two-layer dispersion relation at each
x
for
k
in terms of the
(fixed) complex frequency of the eigenmode. Similarly, the vertical structure
coefficients
AJ
are identical to those
of
the conventional two-layer eigen-
modes corresponding to wavenumber
k
and winds
U,
and
U,
.
The
Aj
are
indeterminate to the extent
of
an overall multiplicative constant; in the
following we shall adopt the convention
IA,12
+
IA2I2
=
1.
The solution in
Eq.
(7) will form the basis of our discussion of the pattern of eddy transports
of heat and vorticity.
3.2.
Strzrcture
Qfthe
Eigenmodes
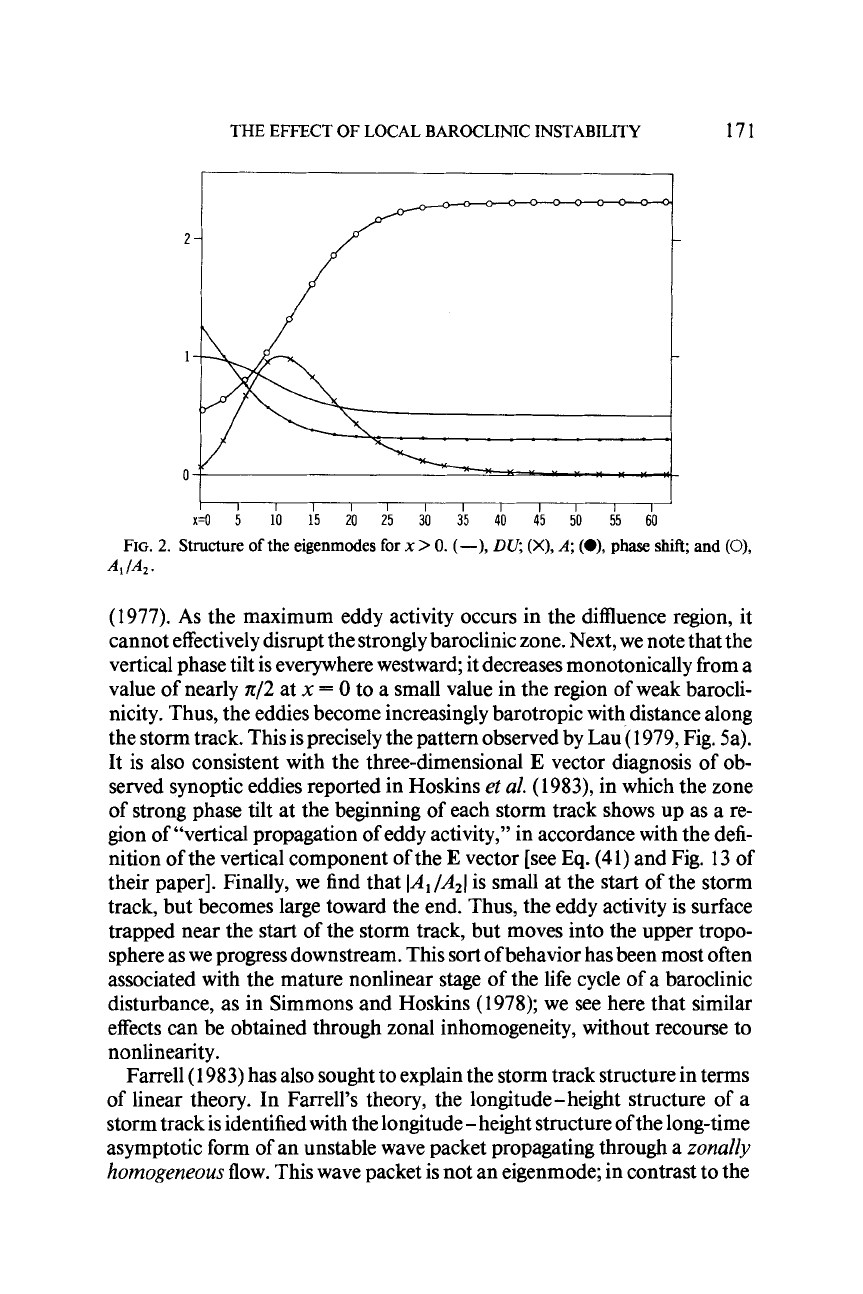
Figure
2
summarizes the three-dimensional structure of the most unstable
eigenmode on the profile
DU(x)
shown by the solid curve. In this calculation,
we set
Cr2
identically to zero, approximating the situation in the real atmo-
sphere. The remaining parameters arep
=
0.25
and
1
=
0.
Results are shown
only for
x
>
0,
as the mode has negligible amplitude at negative x(recal1 that
x
=
0
represents the center of the highly baroclinic zone of the basic-state
jet). It was shown in Pierrehumbert
(
1984) that the wind field upstream
of
the
point of maximum baroclinicity is essentially immaterial to the structure of
the modes. First, we note that the maximum amplitude
A
occurs well down-
stream
of
the site of maximurn baroclinicity. This
is
consistent with the
observed pattern of synoptic eddy variance reported
by
Blackmon
et
al.
THE
EFFECT
OF
LOCAL BAROCLIMC INSTABILITY
171
II
II
II
II
I
II
I I‘
x=O
5
10
15 20 25
30
35
40
45 50 55
60
FIG.
2.
Structure
of
the eigenmodes
for
x
>
0.
(-),
DV;
(X),
A;
(O),
phase
shift;
and
(0),
A,/A,.
(1 977).
As
the maximum eddy activity occurs in the diffluence region, it
cannot effectively disrupt the strongly baroclinic zone. Next, we note that the
vertical phase tilt is everywhere westward; it decreases monotonically from a
value of nearly
n/2
at
x
=
0
to a small value in the region of weak barocli-
nicity
.
Thus, the eddies become increasingly barotropic with distance along
the storm track. This is precisely the pattern observed by Lau
(1 979,
Fig. 5a).
It is also consistent with the three-dimensional
E
vector diagnosis of ob-
served synoptic eddies reported in Hoskins
et
al.
(1983),
in which the zone
of strong phase tilt at the beginning of each storm track shows up as a re-
gion of “vertical propagation of eddy activity,” in accordance with the defi-
nition of the vertical component of the
E
vector [see
Eq.
(41)
and Fig.
13
of
their paper]. Finally, we find that
IA,
/A,J
is small at the start
of
the storm
track, but becomes large toward the end. Thus, the eddy activity is surface
trapped near the start of the storm track, but moves into the upper tropo-
sphere as we progress downstream. This sort of behavior has been most often
associated with the mature nonlinear stage of the life cycle of a baroclinic
disturbance, as in Simmons and Hoskins
(1 978);
we see here that similar
effects can be obtained through zonal inhomogeneity, without recourse to
nonlinearity.
Farrell
(
1983)
has also sought
to
explain the storm track structure in terms
of linear theory. In Farrell’s theory, the longitude-height structure
of
a
storm track is identified with the longitude
-
height structure of the long-time
asymptotic form of an unstable wave packet propagating through a
zonally
homogeneous
flow. This wave packet
is
not an eigenmode; in contrast to the

I72
R.
T.
PIERREHUMBERT
modes we have considered, different parts of the packet grow at different
rates and the whole pattern propagates downstream with time. An observer
at a fixed point in space would see first one part of the pattern and then
another. It thus seems that Farrell’s theory cannot account for the fixed
spatial structure of the storm tracks.
3.3.
Eddy Fluxes and Tendencies
In order to compute the fluxes associated with local instability, one need
only substitute the real part ofthe
WKB
eigenmode
[Eqs.
(7a)-(7c)] into the
flux expressions
[
Eqs.
(4c), (k), and (5d)l and carry out the indicated ensem-
ble averages. The proper definition of the ensemble average is a matter
of
some uncertainty; here, we shall make use of the random-phase ensemble
average introduced by Frederiksen
(
1983), in which the ensemble is taken to
consist of all phases of the eigenmode with equal probability. In the context
of
Eqs.
(7a)
-
(7c), this amounts to an unweighted average of quadratic quan-
tities over the phase
a.
Thus, ifp
=
Pexp(ia) and
q
=
Q
exp(ia), in which
P
and
Q
are independent of
a,
the ensemble average of the product of their real
parts is
(Re(p)Re(d)
=
(1/2)Re(PQ*)
(8)
where the asterisk denotes complex conjugation. The construction of the
local modes was camed out explicitly only for the case
1
=
0
in Pierrehum-
bert
(
1984).
However, when
Z
is smali the lowest order form of the modes can
be obtained by simply multiplying the
f
=
0
solutions
by
the appropriate
sinusoidal modulation in
y.
As a matter of expedience, this approximation
was used in producing the quantitative results presented below.
Upon carrying out the indicated procedure, the components of the baro-
tropic vorticity
flux
are found to
be
F,
=
-(fA2/2)[kf
+
Z2
-
k:]
sin(1y) cos(fy)
F,,
=
-(k,A2/2)[kf
+
k:
-
/*I
COS~(/JJ)
(9a)
(9b)
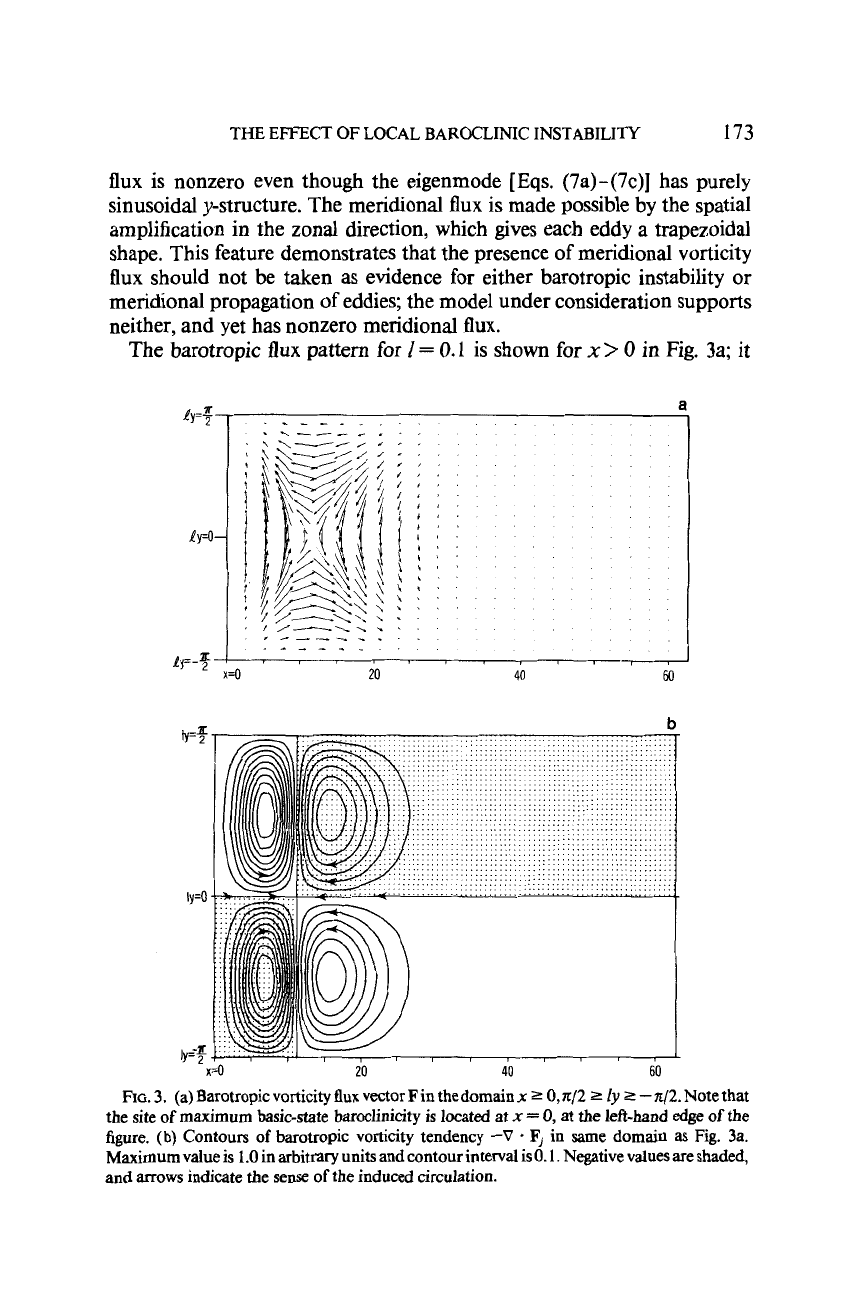
The zonal flux
is
antisymmetric in
y.
North of the centerline of the storm
track,
F,
is negative, provided the spatial amplification rate
k,
is not
so
large
as to dominate the real part
of
the wavenumber. At each
y,
the maximum
magnitude of
F,
occurs near the site of maximum amplitude of the eigen-
mode, since
k,
vanishes and
A
is maximized there. The meridional flux is
symmetric about
y
=
0.
Since
k,
<
0
upstream of the site of peak eigenmode
amplitude and
k,
>
0
downstream, the meridional flux points northward
upstream of the peak and southward downstream of the peak provided the
meridional wavenumber is not too large. It is noteworthy that the meridional
THE
EFFECT
OF
LOCAL BAROCLINIC INSTABILITY
173
flux
is nonzero even though the eigenmode
[Eqs.
(7a)-(7c)J has purely
sinusoidal y-structure. The meridional flux is made possible by the spatial
amplification in the zonal direction, which gives each eddy a trapezoidal
shape. This feature demonstrates that the presence of meridional vorticity
flux
should not be taken
as
evidence for either barotropic instability or
meridional propagation of eddies; the model under consideration supports
neither, and yet has nonzero meridional flux.
The barotropic
flux
pattern for
I
=
0.1
is shown for
x
>
0
in Fig. 3a; it
ay=$
,
a
I
FIG.
3.
(a)BarotropicvorticityfluxvectorFinthedomainxz
O,z/2
2
ly
2
-z/2.Notethat
the site
of
maximum basic-state baroclinicity is located at
x
=
0,
at the left-hand edge
of
the
figure.
(b)
Contours
of
barotropic vorticity tendency
-V
Fj
in same domain
as
Fig. 3a.
Maximum value is
1.0
in arbitrary units and contour interval isO.1. Negative values are shaded,
and
arrows
indicate the sense
of
the induced circulation.
