Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

201

температуру определяют, зная предыдущую. Можно показать, что

оба метода дают правильные результаты лишь при Fо < 1/2 для

одномерной задачи и при Fо < 1/4 — для двумерной (говорят, что

при таких Fо схемы

устойчивы).

При больших значениях Fо явные методы дают физически

необъяснимые решения. Пусть, например, пользуясь соотношением

(2.112), мы задали Fо = 1; тогда

()

1321321

TTTTTTT

−

′

Если в некоторый момент τ Т

– Т

= 500 К, T

= 300 К, то в

момент τ + ∆τ получим

.K500K700300500500

−

′

Теплота к узлу 1 подводилась от более нагретых узлов 2 и 3,

но, согласно второму началу термодинамики, температура узла 1 не

может превысить температуры узлов 2 и 3; полученный выше

результат неверен (говорят, что схема

потеряла устойчивость).

Для сохранения устойчивости нужно вернуться к шагу ∆τ, при

котором Fо < 1/2.

С появлением компьютеров возрос интерес к так называемым

неявным схемам: они позволяют рассчитать поле температуры в

произвольный момент без промежуточных вычислений. Неявные

схемы устойчивы при любых значениях числа Фурье.

Запишем, например, балансовое уравнение (2.111) для

момента τ + ∆τ, когда температуры в узлах 2 и 3 примут значения

и TT

′′

()

(

)

(

)

[

]

1312312111

TTTTQQTTVc

′

−

′

−

′

∆

+=τ

∆

−

′

(2.114)

откуда после преобразований получим

(

)

(

)

,0FoFo1

1321

−

′

−

′

−

′

− TTTT

(2.115)

т. е. температура

′

зависит от температур

и TT

′

соседних

узлов в тот же момент времени. Следовательно, соотношение вида

(2.115) надо записать для всех узлов расчетной области, а затем

решить систему уравнений для интересующего нас момента τ + ∆τ

(другими словами — сразу задать “нужное” число Фурье). При

таком подходе выбор числа Фурье ничем не ограничен. Схема

устойчива при любых шагах

по времени, однако чем меньше ∆τ,

тем точнее результат, поскольку конечно-разностное

алгебраическое уравнение (2.106) становится ближе к

дифференциальному уравнению теплопроводности. Еще раз

напомним, что неявные конечно-разностные схемы практически

реализуют лишь в компьютерных вариантах, в то время как схемы

202

явные можно рассчитывать с помощью калькулятора и даже

строить графически.

2.6. ФИЗИЧЕСКИЕ ОСНОВЫ

КОНВЕКТИВНОГО ТЕПЛООБМЕНА

2.6.1. Основные понятия и определения

Конвективный теплообмен обусловлен совместным

действием конвективного и молекулярного переноса теплоты при

движении теплоносителя относительно твердой поверхности.

В соответствии со вторым началом термодинамики такой

процесс возможен, лишь, если температура поверхности отличается

от температуры теплоносителя. Теплоносителем может быть любая

среда: сжимаемая (газ, пар) или практически несжимаемая

(капельная жидкость). Если скорость движения газа или пара

существенно меньше скорости звука, то сжимаемостью можно

пренебречь; в этом случае используют лишь один термин —

жидкость, относя его к подвижной среде любой физической

природы и агрегатного состояния.

Если движение жидкости вызвано действием неоднородного

поля массовых сил (гравитационных, магнитных, электрических),

то говорят о свободной конвекции. Если на жидкость действуют

внешние силы (приложенные на границе), внутренние однородные

массовые силы или же кинетическая энергия приданы потоку

жидкости извне, то рассматривают вынужденную конвекцию.

Обычно вынужденную конвекцию вызывает принудительная

прокачка жидкости каким-либо нагнетателем — вентилятором,

компрессором или насосом.

Характерные размеры области, где происходит течение

жидкости, почти всегда несоизмеримо велики по сравнению с

длиной свободного пробега ее молекул, поэтому жидкую среду

считают непрерывной. Это означает, что и температура в

жидкости распределена непрерывно, поэтому градиент

температуры и вектор плотности теплового потока сохраняют здесь

тот же смысл, что и в теории теплопроводности. Основная задача

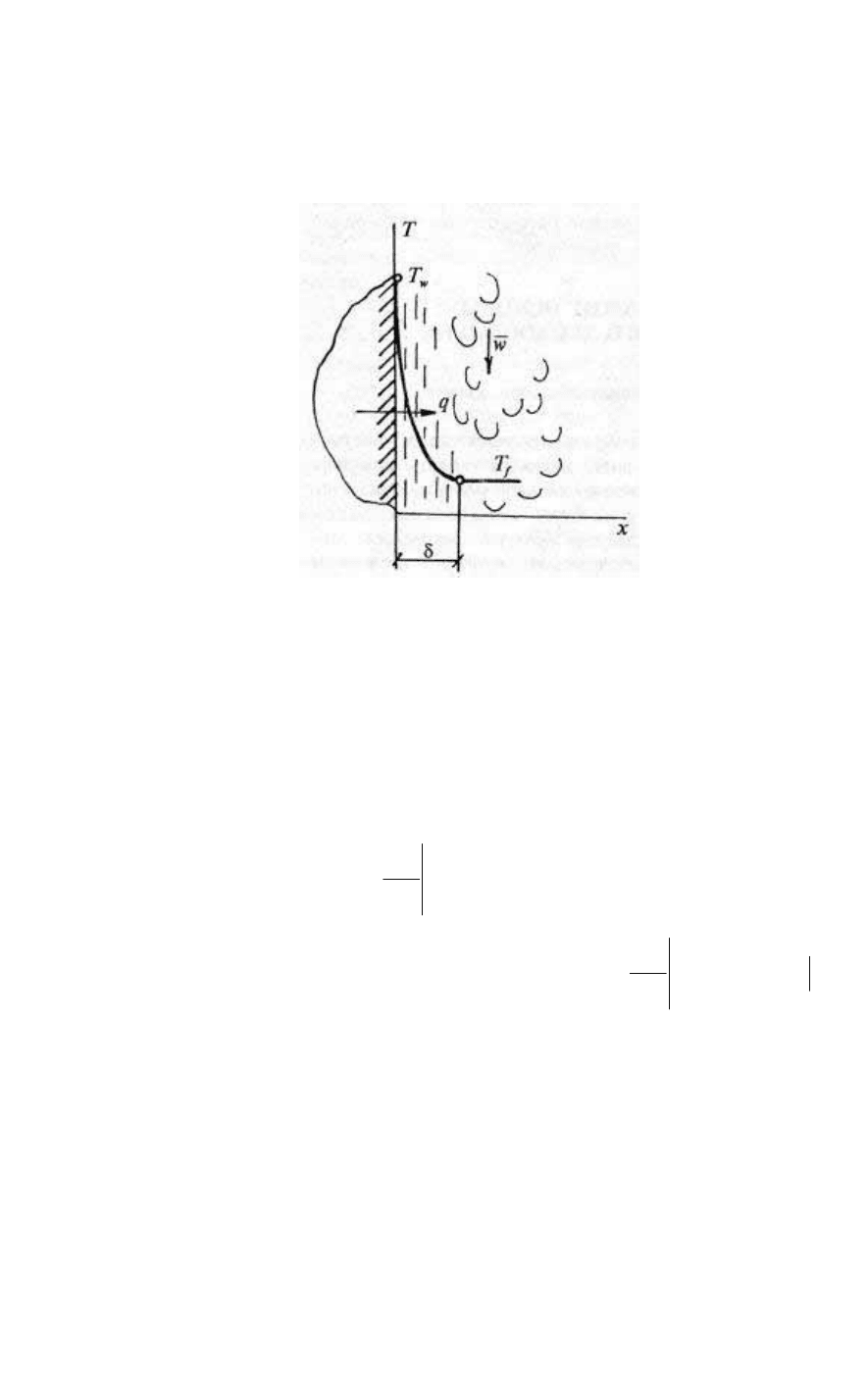
203

теории конвективного теплообмена — выявить связи между

плотностью теплового потока q на границе поверхность —

жидкость, температурой поверхности Т

, и температурой жидкости

(рис. 107).

Рис. 107.

Экспериментально установлено, что в тонком слое вблизи

поверхности жидкость практически не подвижна, и теплота

передается только молекулярным путем. Поэтому в соответствии с

гипотезой Био–Фурье в пристенной области

,λ

∂

−=

(2.116)

где λ

— теплопроводность жидкости;

grad

∂

—

нормальная составляющая градиента температуры жидкости

вблизи поверхности.

Чтобы пользоваться в расчетах формулой (2.116), надо знать

распределение температуры в жидкости, а оно в общем случае

неизвестно. С другой стороны, эксперименты показывают, что

(

)

,α

TTq

−

(2.117)

где α — коэффициент пропорциональности (вспомним, что его

называют коэффициентом теплоотдачи).

204

Коэффициент теплоотдачи α характеризует интенсивность

конвективного теплообмена и численно равен плотности

теплового потока на поверхности раздела, отнесенной к

температурному напору (разности температур) между жидкостью

и поверхностью.

Зависимость (2.117), как уже отмечалось, называют законом

теплоотдачи Ньютона. Название стало общепринятым, хотя

впервые линейную связь плотности теплового потока с разностью

температур жидкости и поверхности экспериментально установил

Ж. - Б. Фурье. Размерность величины α — Вт/(м

⋅К); ее величина

меняется в широких пределах — от 5…30 Вт/(м

⋅К) при свободной

конвекции в газах до 4⋅10

…1,2⋅10

Вт/(м

⋅К) при капельной

конденсации пара.

Первоначально считали, что множитель α характеризует

способность жидкости “отбирать теплоту”. Лишь в конце ХIХ в.

при исследовании теплообмена в трубах паровозных котлов

выяснилось, что α почти линейно увеличивается с увеличением

скорости потока; позднее установили, что α зависит от физических

свойств жидкости, формы поверхности теплообмена и от многих

других факторов. Поэтому закон теплоотдачи Ньютона следует

считать не фундаментальным законом природы, а лишь гипотезой,

подтверждаемой более или менее надежно при правильной оценке

коэффициента теплоотдачи α.

Если на всех участках поверхности плотность теплового

потока q, температуры Т

и Т

. сохраняют свои значения, то

коэффициент α не будет зависеть от координат. В противном случае

определяют средний коэффициент теплоотдачи

()

,α

FTT

wmfm

−

где

wmfmm

TTQ ,,

— средние значения теплового потока Q,

температур Т

и Т

, а F — площадь поверхности теплообмена.

Иногда рассматривают местный коэффициент

теплоотдачи — коэффициент теплоотдачи в данной точке

205

поверхности теплообмена, равный местной плотности теплового

потока q

, отнесенной к местному температурному напору Т

– Т

;

()

.α

wifi

−

Если известны коэффициенты α

, и участки поверхности

теплообмена F

, в пределах которых α

= const, то общий тепловой

поток

()

∑∑

−==

iwifii

FTTFqQ

.α

Чем меньше участки F

, тем точнее удается рассчитать Q

предельном (и самом общем) случае тепловой поток определяют

интегрированием по всей поверхности

∑

(

)

,dα FTTQ

∫

−=

где

TT ,,α

— величины, определенные в окрестностях элемента

площади dF.

Из уравнений (2.116) и (2.117) следует, что

)(

−

∂

−

(2.118)

Уравнение (2.118) называют уравнением теплоотдачи.

Обычно температура Т

принимает постоянное значение на

некотором удалении от стенки δ, которое называют толщиной

теплового пограничного слоя (см. рис. 107). Если в первом

приближении считать, что

−

−=

∂

то в соответствии с равенством (2.118) получим

206

)(

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

(2.119)

Уравнение (2.119) можно использовать для качественных

оценок, если известен хотя бы порядок величины δ. Из равенства

(2.119) следует, кроме того, что для увеличения значения α надо

выбирать жидкость с большей теплопроводностью λ

Кроме

теплопроводности λ

на величину α влияют и другие физические

свойства жидкости: плотность ρ

, изобарная теплоемкость c

динамическая вязкость µ, температурный коэффициент объемного

расширения β (в последних двух случаях индекс f опущен,

поскольку эти величины определены только для жидкости).

Величины ρ

, λ

, c

рассмотрены в разделе 1 и 2.1, сделаем

дополнительно несколько замечаний о величинах µ и β.

Динамическая вязкость µ, Па⋅с, характеризует силы взаимо-

действия между слоями жидкости, движущимися с различной

скоростью. Вязкость связана с внутренним трением в жидкости.

И. Ньютон установил закон вязкого трения, согласно которому

касательная сила s, отнесенная к поверхности, пропорциональна

градиенту скорости

∂

вблизи этой поверхности:

.µ

∂

(2.120)

При 1=

∂

и µ = s, т. е. динамическая вязкость µ

характеризует силу трения, приходящуюся на единицу поверхности

контакта "соседних" слоев жидкости, при единичном градиенте

скорости.

Как и предыдущий закон Ньютона (2.117), закон вязкого

трения (2.120) — скорее, феноменологическая гипотеза, поскольку

величина µ зависит от температуры и некоторых других факторов.

Для капельных жидкостей величина µ почти не связана с давлением

и снижается по мере повышения температуры. Для газов значение µ

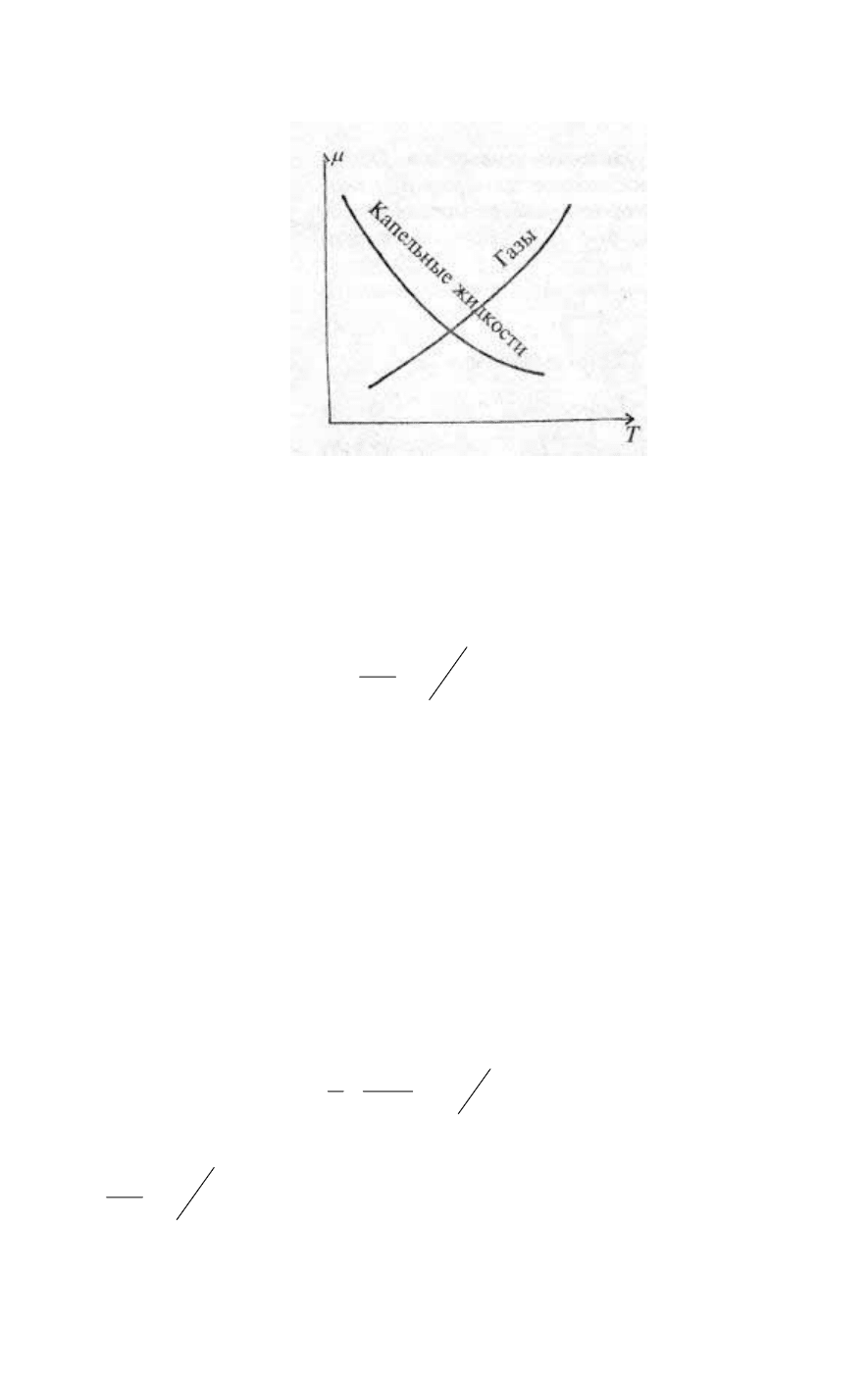
207

с повышением температуры возрастает (рис. 108), а с увеличением

давления изменяется слабо.

Рис. 108.

Иногда вместо динамической вязкости µ используют

кинематическую вязкость:

Для капельных жидкостей значение ν меняется с темпера-

турой почти так же, как и µ, но для газов ν сильно зависит от

давления. Надо помнить: если теплоносителем является газ,

следует выбрать из таблиц значения µ(Т), а затем пересчитать

величину ν по плотности ρ

(Т), определенной параметрами

состояния газа р, Т и его газовой постоянной R.

Температурный коэффициент объемного расширения

⎟

⎠

⎞

⎜

⎝

⎛

∂

где

кг

v = — удельный объем теплоносителя; р, Па — его

давление.

Для газа, близкого к идеальному, β = 1/Т, где Т —

абсолютная температура газа.

208

Для количественного описания конвективного теплообмена

нужно составить замкнутую систему дифференциальных

уравнений. При этом, как и в теории теплопроводности, делают

некоторые предварительные допущения.

1. Жидкость, участвующая в конвективном теплообмене,

является сплошной средой.

2. В потоке жидкости выполняются законы сохранения

энергии, массы и количества движения.

3. В качестве дополнительных гипотез используют: связь

между тепловым потоком и разностью температур (2.117);

связь между трением и градиентом скорости (2.120).

4. Физические свойства (динамическую вязкость µ, плотность

изобарную теплоемкость c

, температурный коэффициент

объемного расширения β, теплопроводность λ

) считают заданными

функциями состояния жидкости.

2.6.2. Дифференциальные уравнения конвективного

теплообмена

По сути дела, одно из таких уравнений мы уже получили —

это дифференциальное уравнение теплоотдачи (2.118). В него

входит неизвестная величина

∂

, которую можно определить,

зная уравнение поля температуры в жидкости:

),τ,,,( zyxTT

(2.121)

где τ,,,

— текущие координаты элементарного объема

жидкости и текущее время.

В неподвижной среде вид функции (2.121) определяет краевая

задача теплопроводности. Если жидкость движется, то координаты

любого элементарного объема

,, будут меняться во времени τ,

поэтому

[]

.τ),τ(),τ(),τ( zyxTT

(2.122)

209

Из равенства (2.122) следует, что полная производная

температуры по времени (так называемая субстанциональная

производная

должна иметь вид

τzτττdτ

∂

zTy

TTT

но производные

zyx

∂

— это проекции скорости

элементарного объема

на координатные оси, поэтому

zτdτ

∂

zyx

В этом равенстве

τ∂

∂T

—

локальная составляющая изменения

температуры во времени, а сумма

z∂

∂

zyx

—

конвективная составляющая.

Дифференциальное уравнение, аналогичное уравнению

теплопроводности для неподвижной среды, выражает закон

сохранения энергии при конвективном теплообмене, его называют

уравнением энергии

pff

dτ

∇=

⎟

⎠

⎞

⎜

⎝

⎛

∂

(2.123)

(здесь

pff

cρ

— температуропроводность жидкости).

Производная

dτ

названа субстанциональной потому, что

характеризует изменение температуры, вызванное движением

материальной среды (субстанции).

210

Из формул (2.122) и (2.123) следует, что изменение темпе-

ратуры жидкости зависит от скорости ее движения:

→→→→

k + wj + wi = ww

zyx

где ,,

→→→

kji — единичные орты.

Скорость w

→

вообще говоря, неизвестна, поэтому

совокупность уравнений (2.118) и (2.123) остается незамкнутой.

Необходимо дополнить ее уравнением, описывающим движение

жидкости. Это дифференциальное уравнение называют

уравнением движения, или уравнением Навье-Стокса; в его

основе — условие равновесия в подвижном объеме жидкости:

dτ

∑

(2.124)

где

∑

— сумма сил, действующих на объем dV; V

ρ — масса

элементарного объема dV,

zdτ

∂

→→→→→

zyx

— субстанциональная производная скорости (ускорение объема

dV). Уравнение (2.124) представляет собой второй закон Ньютона

для движущегося элемента жидкости. Рассмотрим силы р

входящие в правую часть этого равенства.

На элемент несжимаемой жидкости действуют силы давления,

вязкости и тяжести (рис. 109).