Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

340 10. Nonbonded Computations

Linear Approximations to the PB Equation; Debye-H¨uckel Theory

For the case of dilute or moderate solutions (e.g., molar concentrations c

−3

M) and low ﬁxed charge, it is possible to approximate the PB equation us-

ing results from Debye-H

uckel theory (see [131, 275, 537, 547], for example, for

introductions). Speciﬁcally, a linearized approximation to the PB equation can be

used to represent the ionic atmosphere of a solute immersed in aqueous solution

and counterions.

A linearized version of the PB equation (eq. (10.58)) can be obtained by a

Taylor-series expansion of the Boltzmann factor with a truncation beyond the

ﬁrst-order terms:

exp[−q

Φ(x)/k

T] ≈ 1 −[q

Φ(x)/k

T] . (10.59)

The linearized version is justiﬁed when

Φ(x)  k

T ,

that is, when energies are much smaller than the thermal energy. This often

holds for monovalent electrolytes and weak source charges (dilute solution), as

mentioned above.

In the special case of spherical symmetry about the origin for the distribution

of charges, the potential Φ depends on the distance r of the point from the ori-

gin. Linearization of the PB equation yields the following linear second-order

differential equation for Φ(r) [537]:

∇

Φ(r)=κ

Φ(r) , (10.60)

where

8πN

1000 k

. (10.61)

Here N

is Avogadro’s number, ρ

is the solvent density, e is the protonic charge

(4.803 ×10

−10

esu), and  is the solvent dielectric constant. The ionic concentra-

tion c

is measured in molar units as a sum over all molar concentrations per liter

of solution, c

, associated with charges (or valences) q

: c



i=1

The linearized PB equation as expressed in eq. (10.60) with (10.61) can be

solved to determine the effective potential Φ at a distance r from a central ion.

Recall that the Coulomb potential q/(r) is produced at a point separated by dis-

tance r from an isolated central ion, which is represented as a uniform charged

sphere of radius a

in a medium of dielectric constant . The Debye-H¨uckel solu-

tion for the modiﬁed electrostatic potential representing the inﬂuence of the ionic

atmosphere is (e.g., [537]):

Φ(r)=B(κ)

q exp(−κr)

r

, (10.62)

We can also write





Φ(r)=κ

Φ(r).

10.6. Continuum Solvation 341

where B(κ) is the salt-dependent coefﬁcient

B(κ)=exp(κa

)/(1 + κa

) . (10.63)

Thus, Debye-H¨uckel theory produces an effective electrostatic potential in

which the Coulomb interactions are screened by ions. The theory predicts the

range of electrostatic inﬂuence of a central ion to be the Debye screening length

−1

.Inotherwords,κ

−1

is the characteristic distance of exponential screening.

From eq. (10.61), we see that the screening parameter κ is proportional to

the square root of the ionic concentration c

. For 1:1 electrolytes (monova-

lent:monovalent salts like NaCl),

κ ≈ 0.33

√

−1

(10.64)

at room temperature (25

), with  =78.5.

For dilute solutions, or κa

 1,wehaveB(κ) ≈ 1; it follows that

the Coulomb screening — reduction of the unscreened potential by the factor

exp(−κr) — reﬂects the reduced effective charge ρ on the central ion due to

counterion accumulation. For physiological ionic strengths, such as 0.15M, the

Debye length is approximately 8

A; this distance represents considerable damping

of Coulomb interactions.

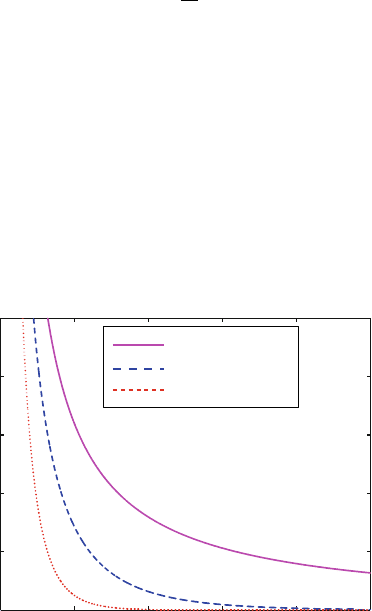
Figure 10.10 compares the Coulomb potential (1/r) to the screened Coulomb

potential (B(κ)exp[−κr]/r) for two values of κ corresponding to c

=0.15M

0 20 40 60 80 100

0.2

0.4

0.6

0.8

x 10

−3

Coulomb vs. Debye−Hückel Potentials

r (Ang)

Coulomb

DH,c

= 0.015 M

DH,c

= 0.15 M

Figure 10.10. Screened Coulomb potentials at two values of the Debye length. The

Coulomb potential (1/r) is compared to the screened Coulomb potential of form

B(κ)exp[−κr]/r as a function of distance r for two values of κ. These two values are

set according to eq. (10.64)forc

=0.15M and 0.015M monovalent salt concentrations,

with coefﬁcients B(κ) computed according to eq. (10.63) (the coefﬁcients are very close

to 1). The two κ values (0.128 and 0.040

A, respectively) correspond to Debye lengths of

about 8 and 25

342 10. Nonbonded Computations

and 0.015M monovalent salt, where the Debye lengths are about 8 and 25

respectively.

The DH approximation has been applied to long DNA for exploring confor-

mational stability and mobility as a function of monovalent ionic concentrations

in the natural cellular environment (e.g., [1125, 1309]). Models are based on the

pioneering work of Stigter, who modeled DNA as charged cylinders [1223]and

reproduced the experimentally-observed dependence of the effective diameter of

DNA on salt concentration by a tail approximation to the PB equation. Extensions

of such DH approximations to macroscopic models of protein/DNA systems have

been described [109] and applied to model chromatin [108].

General Solutions to the Poisson-Boltzmann Equation

Many practical procedures have been developed to solve the PB equation nu-

merically, including solutions of its various approximations (e.g., [16, 80, 563,

610,813, 903, 1058, 1178]); see also references cited in [81], and [303,1023]for

applications to calculate charge distributions. The linearized approximations are

useful in many cases, as mentioned above. For high charge density (such as for

polyelectrolyte DNA) and high salt concentrations, the nonlinear PB version is

preferred.

Numerical solutions are typically obtained through ﬁnite-difference or ﬁnite-

element (or boundary element) methods. Both involve a discretization of the

(irregular) biomolecular domain in 3D, so that the potential, charge density, and

dielectric constant are deﬁned at grid points ( is usually deﬁned over broader

domain regions). The dielectric constant is assigned appropriate values depend-

ing on its proximity to the solute, though a two-dielectric model is typically used

— to distinguish the inside region, near the solute, from the outside region, far

from the solute. The ﬁnite-difference solution can be obtained iteratively by var-

ious linear algebra solvers (e.g., linear conjugate gradient method, Gauss-Seidel,

or Successive Over Relaxation methods) [16, 903,1058].

The resulting quality of the numerical solutions depends on the various assump-

tions made and settings used. The convergence of the solvers also depends on

such parameters as the grid size, initial charge and  assignments, and algorithmic

parameters.

An analytical gradient minimization method based on a ﬁnite-element dis-

cretization for solving the PB equation has also been presented [429]. While the

DelPhi program uses a regular cubic grid, this gradient-based approach uses an

adaptive grid so as to include more grid points at the solvent-accessible surface,

where the dielectric value is changing rapidly. Overall, preliminary comparisons

show that the computational efﬁciency of both approaches is comparable [429];

the gradient-based method is also used for geometry optimization applications,

serving as an improvement to gas-phase molecular mechanics minimizations

since solvation effects are included.

Popular packages used in the biomolecular community are those developed at

research groups at Columbia University (DelPhi and GRASP) and the University

10.6. Continuum Solvation 343

of Houston (UHBD, now at UCSD, which includes segments for Brownian dy-

namics). The latter has been used to study huge macromolecular systems [81](see

also Figure 10.11).

The APBS (Adaptive PB Solver) program is also popular [81] and can be

used on its own or in conjunction with other molecular modeling packages like

CHARMM or AMBER, with results visualized with popular graphics programs

like VMD or PYMOL. In addition, web tools like PBEQ based on the PB solver

in CHARMM [610]orMark-US (a functional assessment tool for proteins) from

the Honig lab make applications easier to users by combining PB solvers with

interactive visualization modules.

Classical electrostatics solutions can provide useful information on charge

distributions around macromolecules (e.g., [303, 1023]), speciﬁc localization of

charged and polar groups in biomolecular systems (e.g., [790, 1253]), the shape

of molecular surfaces, and the relation between salt effects and conformational

changes (e.g., [1125]). Effects of the ionic atmosphere on intermolecular bind-

ing associations, such as between proteins and ligands, can also be analyzed

[565,1057].

Effective numerical packages such as DelPhi and UHBD, combined with ad-

vanced graphical rendering programs, offer valuable modeling tools for exploring

the effects of electrostatics and solvation on molecular structure and function.

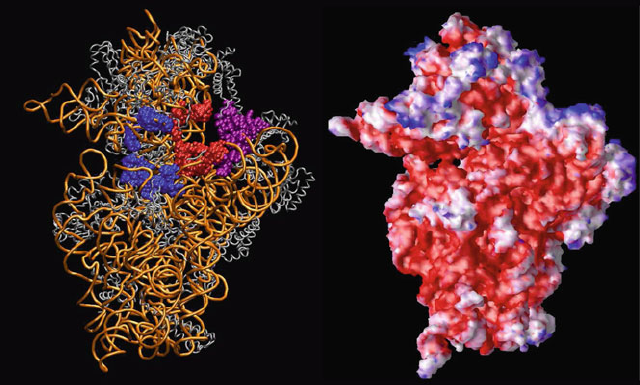
Figure 10.11. The electrostatic environment of the 30S ribosomal unit as computed by

the linear PB equation at 150 mM ionic strength with a solute dielectric of 2 and solvent

dielectric of 78.5 [81]. The protein (silver) and nucleic acid (gold) atoms are distinguished

on the left, with selected components of A, P, and E sites shown in blue, red, and purple

respectively. At right, the electrostatic potential mapped on the 30S surface is rendered in

blue (positive) and red (negative) to illustrate regions with values greater than 2.6 k

T/e

and less than −2.6 k

T/e, respectively.

344 10. Nonbonded Computations

The electrostatic analysis of a ribosomal unit is shown in Figure 10.11.(Seealso

analysis of the nucleosome core particle in Chapter 6).

Algorithmic Challenges

Recent algorithmic advances — by adaptive ﬁnite element methods [80,563]tai-

lored to multiprocessor systems [81] — allow solutions of the linear PBE for very

large systems of order one million atoms. Figure 10.11 illustrates the PB solution

for the 30S ribosome subunit.

A future goal in the ﬁeld is repeated solution of the PBE, for example in the

course of a dynamic simulation.

Multivariate Minimization

in Computational Chemistry

Chapter 11 Notation

YMBOL DEFINITION

Matrices

A symmetric matrix, components {A

}



approximation to Hessian inverse at x

(QN methods)

scaling matrix at step k of minimization method (trust

region approach)

Hessian matrix, components H

(x) ≡ ∂

f(x)/∂x

∂x

I identity matrix

preconditioning matrix, related to H (TN methods)

preconditioning matrix at step k of TN method

QN low-rank update matrix at step k

Vectors

b, y constant vectors

unit vectors

gradient vector of f, components g

(x) ≡ ∂f(x)/∂x

gradient vector at x

(short hand for g(x

))

search vector at step k of minimization method

inner-loop CG iterate j for outer-loop search vector

(TN method)

residual vector deﬁned in TN methods (Mz = r)

displacement vector at step k, x

k+1

− x

(QN method)

vector of n components {x

}

starting point vector for minimization

minimization iterate at step k of method

∗

local minimum point of objective function

gradient difference vector at QN step k, g

k+1

− g

z solution vector deﬁned in TN methods (Mz = r)

T. Schlick, Molecular Modeling and Simulation: An Interdisciplinary Guide, 345

Interdisciplinary Applied Mathematics 21, DOI 10.1007/978-1-4419-6351-2

11,

 Springer Science+Business Media, LLC 2010

346 11. Multivariate Minimization in Computational Chemistry

Chapter 11 Table (continued)

YMBOL DEFINITION

Scalars & Functions

a, b numbers

(x) constraint function i

small positive number (in TN methods)

constant (function value)

f(x)

objective function, dependent on vector x

small number (ﬁnite difference interval)

problem dimension

convergence order

q(x)

quadratic function

(s) quadratic model of objective function

residual norm at step k of TN methods

line search parameter for sufﬁcient decrease condition

line search parameter for sufﬁcient decrease of curvature

(also convergence ratio)

scheme-dependent scale parameter of search vector p

(CG and QN methods)



,

small positive numbers



small positive number, machine precision

forcing sequence in TN methods

line search steplength

trial line search steplength

variable in the neighborhood of x for a univariate

function f(x)

φ(λ)

polynomial of steplength λ

size bound in QN methods at step k

’Pon my word Watson, you are coming along wonderfully. We

have really done very well indeed. It is true that you have missed

everything of importance, but you have hit upon the method.

Arthur Conan Doyle (1859–1930), in A Case of Identity (1891).

Economic forecasting makes weather forecasting look like physics.

Ben Bernanke, 26 July 2009.

[Bernanke, the US Federal Reserve Chairman, spoke about the current

economic crisis in a town-hall forum in Kansas City, MO, hosted by the

PBS NewsHour’s Jim Lehrer.]

11.1. Ubiquitous Optimization: From Enzymes to Weather to Economics 347

11.1 Ubiquitous Optimization: From Enzymes

to Weather to Economics

Optimization is a fundamental component of molecular modeling. The deter-

mination of a low-energy conformation for a given force ﬁeld can be the ﬁnal

objective of the computation. It can also serve as a starting point for subsequent

calculations, such as molecular dynamics simulations or normal-mode analyses.

Both local and global optimization problems lie at the heart of numerous sci-

entiﬁc and engineering problems — from the biological and chemical disciplines

to architectural and industrial design to economics. Optimization is part of our

everyday life — responsible for our weather forecasts, ﬂight planning, telephone

routing, microprocessor design, and the functioning of enzymes in our bodies.

11.1.1 Algorithmic Sophistication Demands Basic Understanding

The mathematical techniques developed to address these optimization problems

are just as robust and varied as the target problems themselves. The algorithmic

complexity of such techniques has led to many available computer programs that

require minimal input from the user (e.g., the starting point and a routine for

function evaluation).

However, the prudent user of these canned software modules — even within

standard molecular mechanics and dynamics packages — should understand the

fundamental structure of the optimization algorithms and associated performance

issues to make their application both efﬁcient and correct, in terms of the physical

interpretations.

This chapter introduces key optimization concepts for this purpose. We also

highlight the fundamentals of local optimizers for large-scale nonlinear un-

constrained problems, an important optimization subﬁeld relevant to biological

macromolecules. We describe the most promising approaches among them, and

discuss practical issues, such as parameter variations and termination criteria.

Of course, the latter are best learned by experimentation in the context of real

problems. To illustrate behavior for complex problems, some comparisons among

three competitive minimizers are also included, for molecular models minimized

in the molecular mechanics and dynamics program CHARMM.

11.1.2 Chapter Overview

Speciﬁcally, Section 11.2 introduces optimization fundamentals such as problem

formulation and terminology. Section 11.3 describes the basic algorithmic frame-

work of iterative minimization protocols (based on line search and trust region

methods); it also discusses convergence criteria and line search procedures and

introduces the key concept of descent directions.

In Section 11.4, we present the Newton method, including a historical per-

spective, and one-dimensional implementations for nonlinear equations as well

348 11. Multivariate Minimization in Computational Chemistry

as optimization. This presentation familiarizes readers with the Newton method

framework — the basis for formulating many other optimization methods — and

with performance and convergenceissues relevant to minimization of multivariate

functions.

In Section 11.5, we mention effective methods for large-scale nonlinear op-

timization, namely quasi-Newton (QN), nonlinear conjugate gradient (CG), and

truncated Newton (TN) schemes. Section 11.6 outlines available software and

presents comparative performance in CHARMM for two molecular models

(a small model system and a protein). Finally, in Sections 11.7 and 11.8,we

summarize recommendations to optimization practitioners and offer a future

perspective to ﬁeld developments.

For details, as well as for other categories of the rich and exciting ﬁeld of

optimization, I refer readers to classic texts [297, 407, 459, 789, 918], some re-

views [417, 915, 1104, 1108, 1131], and a perspective [1390]. In recent years,

optimization methods have become increasingly important in material science and

nanotechnology, for ﬁnding the favored structure of materials, including biologi-

cal systems. Such problems are typically solved by global optimization problems,

as recently reviewed [196].

11.2 Optimization Fundamentals

The methods for solving an optimization task depend on the problem classiﬁca-

tion. Since the value of the independent variable that maximizes a function f also

minimizes the function −f, it sufﬁces to deal with minimization.

The optimization problem is classiﬁed according to the type of indepen-

dent variables involved (real, integer, mixed), the number of variables (one,

few, many), the functional characteristics (linear, least squares, nonlinear, non-

differentiable, separable, etc.), and the problem statement (unconstrained, subject

to equality constraints, subject to simple bounds, linearly constrained, nonlin-

early constrained, etc.). For each category, suitable algorithms exist that exploit

the problem’s structure and formulation.

11.2.1 Problem Formulation

For a vector x of n components {x

}, we write the minimization problem as:

min

{f(x)} , x ∈D, (11.1)

where f is the objective function and D is a given region (which can be the entire

Euclidean space 

). The problem can be subject to m constraints, which can be

written more generally as a combination of equality and inequality constraints:

(x)=0 fori =1,...,m



(x) ≤ 0fori = m



+1,...,m. (11.2)

11.2. Optimization Fundamentals 349

This general formulation can be obtained for problems with bound constraints in

the form

(x)=x

where x

is the ith component of the vector x, or for problems with two-sided

constraints such as

≤ c

(x) ≤ u

In this chapter, we only cover unconstrained optimization formulations. For a

comprehensive review of interior methods for continuous nonlinear optimization

problems subject to constraints, see [417].

11.2.2 Independent Variables

In most computational chemistry problems, x is a real vector in Euclidean space,

i.e., x ∈

,andf deﬁnes a transformation to a real number,i.e., f(x):

→.

When the components of x are integers, the optimization problem is classiﬁed

as integer programming.Whenx is a mixture of real and integer variables, the

problem is of mixed-integer programming type. Common examples of integer pro-

gramming are network optimization and the ‘traveling salesman problem’,

also

classiﬁed as combinatorial optimization. See [1390], for example, and references

cited therein.

11.2.3 Function Characteristics

The nature of the function f is the next step in problem classiﬁcation. Many appli-

cation areas such as ﬁnance and management-planning tackle linear or quadratic

objective functions.

Linear and Quadratic Functions

Linear objectives can be written in vector form as

f(x)=b

x + f

, (11.3)

where b is a column vector of dimension n,andf

is a scalar. Quadratic objective

functions can be expressed as

f(x)=x

Ax + b

x + f

, (11.4)

The notorious ‘traveling salesman’ problem seeks to ﬁnd the optimal travel route that covers

a given number of cities, each one only once, and returning to the home town. Visually, imagine

drawing such a route on a map, where each city k for k =0,...,n is designated by coordinates

}. The connected route started at {x

} covers each city and returns to the original point.

Though simple to envision, there are clearly many such routes, and the number of combinations that

connect all these cities grows steeply with n. This problem in fact belongs to a class of very difﬁcult

problems (known as NP-complete) for which no polynomial-complexity algorithm is known (i.e., the

computational time for an exact solution of this problem increases exponentially with n).