Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide
Подождите немного. Документ загружается.


320 10. Nonbonded Computations
equation, also written as ∇
2
u =0or Δu =0.TheLaplacian is a differential operator
from scalar to scalar fields whereas the divergence is a differential operator from vector to
scalar fields.
10.4.4 Finite-Dielectric Correction
The decomposition above, while convergent, is strictly correct only for an infinite
dielectric ( = ∞) medium or for unit cells with a zero dipole moment. The cor-
rection term (E
cor,
) for a nonuniform field associated with a macroscopic crystal
in a dielectric continuum with external dielectric constant was only derived 60
years after Ewald’s original derivation [293], and yields:
E
cor,
= E
coul
( =1)− E
coul
( = ∞)=
2π
3L
3
N
j=1
q
j
x
j
2
. (10.36)
Though reliable, Ewald’s algorithm as corrected in [293] was still O(N
2
) in com-
putational complexity. This is because the long-range reciprocal-space Fourier
sum requires O(N
2
) to be a sufficiently accurate approximation for large β (see
below).
10.4.5 Ewald Sum Complexity
The key breakthroughs for reducing the computational complexity of the Ewald
sum came in two steps.
Optimization of β
First, by optimizing the parameter β that controls the width of the screen-
ing Gaussians (see Figure 10.7), the relative convergence rates of the real and
reciprocal-space series are adjusted to optimize the work involved [402]. Namely,
as β increases, the real-space sum converges more rapidly and the reciprocal
sum more slowly. Both sums are truncated in practice (finite number of terms).
Thus, for example, a sufficiently large β yields an accurate direct-space sum
with an appropriate truncation, resulting in O(N ) work for the direct-space sum
rather than O(N
2
); however, the reciprocal-space sum still requires O(N
2
) work.
The optimal work balance between the two components can yield an overall
O(N
3/2
) method by adjusting β [991]. This is much better than O(N
2
) but still
considerably expensive for large biomolecular systems.
Mesh Interpolation
The second breakthrough in the Ewald sum came by noting that the trigonometric-
function values in the Fourier series used to represent the reciprocal-space term
10.4. The Ewald Method 321
can be evaluated through a smooth interpolation of the potential over a regular
grid. The resulting particle-mesh Ewald (PME) method reduces the overall com-
putation to O(N log N). The smoothing can be done by Lagrange interpolation
[284] or by B-spline interpolation [369].
Variations
Credit for this interpolation idea is due to Hockney and Eastwood who devel-
oped several methods in the early 1970s for simulations of hot gas plasmas in
fusion machines. Included is a ‘particle-particle particle-mesh’ (P
3
M) scheme, as
detailed in their text [554]. The P
3
M method for evaluating long-range forces in
large systems splits the interparticle force summation into a short-range, rapidly-
varying part and a smooth, slowly-varying remainder. A direct ‘particle-particle’
sum is used to compute the former, while a ‘particle-mesh’ interpolation proce-
dure is used to approximate the latter on a uniform grid. A ‘Q-minimizing’ method
is also used to optimize the scheme’s parameters (given a desired accuracy), such
as mesh size, cutoff radius, and charge assignment scheme.
The P
3
M method and its cousins are thus closely related to the fast PME
schemes used in biomolecular dynamics. Application of the P
3
M scheme as de-
scribed in [554] to molecular dynamics has also demonstrated good performance
[792, 793], with guidelines for the scheme’s parameters obtained by optimizing
an auxiliary function.
10.4.6 Resulting Ewald Summation
Following a series of mathematical manipulations (see [1267], for example), the
resulting composition of the Ewald summation for E
coul
of eq. (10.24)at =1
has five terms:
E
coul
= E
real
+ E
recip
+ E
cor,self
+ E
cor,ex
+ E
cor,
. (10.37)
The first term, E
real
, corresponds to a real-space (or direct) sum of the electro-
static energy due to the point charges screened by oppositely-charged Gaussians.
The second sum, E
recip
,istheassociated canceling term (periodic sum
of Gaussians) summed in reciprocal space using smooth interpolation of
Fourier-series values. The last three terms are correction terms.
The first correction (which is position independent) subtracts the self-
interaction term (each point charge and its corresponding Gaussian charge cloud)
which is included in the first two terms. The second correction subtracts the
Coulomb contribution from the nonbonded pairs excluded from the Coulomb
energy (denoted as pairs i, j ∈ Ex below) since they are separately accounted for
in bonded, bond-angle, and possibly dihedral-angle terms. The third correction
accounts for the non-infinite dielectric medium (eq. (10.36)).
322 10. Nonbonded Computations
Following algebraic manipulations, the resulting Ewald sum can be expressed
as follows:
E
real
=
1
2
N
i,j=1
q
i
q
j
|n|
erfc (β |r
ij
+ n|)
|r
ij
+ n|
; (10.38)
E
recip
=
1
2πL
3
|m|=0
exp(−π
2
|m|
2
/β
2
)
|m|
2
S(m) S(−m) , (10.39)
where S(m)=
N
j=1
q
j
exp [2πim · x
j
]; (10.40)
E
cor,self
=
−β
√
π
N
j=1
q
2
j
; (10.41)
E
cor,ex
= −
1
2
N
i,j∈Ex
q
i
q
j
erf (β |r
ij
|)
|r
ij
|
; (10.42)
E
cor,
=
2π
(1 + 2) L
3
N
j=1
q
j
x
j
2
. (10.43)
The erfc function decays to zero with increasing values of the independent
variable. If β is sufficiently large, the only term that contributes to the real-space
sum is for |n| =0, and it can be computed in practice with a spherical cutoff of
order b =10
˚
A.
The reciprocal space or Fourier term corresponds to a summation over the re-
ciprocal vectors m , where the Fourier terms S(m) are charge-weighted structure
factors (see Box 10.1). Eqs. (10.39)and(10.40) can also be written as:
E
recip
=
1
2πL
3
N
i,j=1
q
i
q
j
|m|=0
exp(−π
2
|m|
2
/β
2
)
|m|
2
exp[2πim · (x
j
− x
i
)] .
(10.44)
When the charges are interpolated over a uniform set of grid points, these structure
factors are easily computed by FFTs.
10.4.7 Practical Implementation: Parameters, Accuracy,
and Optimization
Gaussian Width
In practice, the Gaussian width parameter β is determined so that the real-space
term achieves a desired accuracy tolerance. In typical solvated proteins or DNA
simulations, β has an order of magnitude of roughly 10/L (L ranges roughly

10.4. The Ewald Method 323
from 60 to 100
˚
A; values exceeding 70
˚
A have been implicated with smaller
artifacts from the enforced periodicity [580]). The effective cutoff used for the
real-space interactions is around 10 to 12
˚
A. When multiple-timestep schemes
are implemented for molecular dynamics, the parameter β (or the cutoff for the
direct-space term) may be further optimized to distribute the work for the real
and reciprocal terms appropriately, so as to yield the greatest overall speedup; see
[97], for example.
Grid Size and Accuracy
The reciprocal-space uses multidimensional piecewise interpolation (e.g.,
B-splines) for evaluating the Fourier terms, with grid size and number of terms
chosen to achieve the desired accuracy. For instance, moderate accuracy (e.g.,
10
−4
relative force error) might be achieved with a coarse interpolation grid
(1 to 2
˚
A). Very high accuracy (e.g., 10
−10
relative force error) might be obtained
with a finer grid (∼0.5
˚
A). The reciprocal-space energy and force terms are
expressed as convolutions and can thus be evaluated quickly using FFTs.
4
Work
has also shown that the finite number of wave vectors used in the discrete ap-
proximation gives rise to truncation errors due to the exclusion of intramolecular
interactions [1019]; this, and the related existence of fast terms in the reciprocal-
force component [97, 98, 1025, 1236], create a problem for development of
efficient multiple-timestep integrators for molecular dynamics simulations using
PME approximations [89].
Computer Architecture Considerations
In the implementation of the PME method on multiprocessors, the cutoff ra-
dius used for the direct sum may be increased to balance the work between
the real-space and reciprocal-space components. This accelerates the computa-
tions because 3D FFTs are challenging to parallelize well. In contrast, the direct
sum parallelizes easily by spatial decomposition. Using a larger cutoff in the
real-space sum reduces the number of lattice vectors (Fourier terms) needed
for the same accuracy in the reciprocal sum and therefore improves the overall
performance.
Experience to date shows that PME implementations for biomolecules —
especially when tightly adapted to the computer architecture — are very fast; the
best implementations require about the same work as needed to evaluate the same
periodic version of the potential but with cutoffs in the range of 10–12
˚
A[1133].
Figure 10.8 shows performance times for an efficiently distributed PME code by
John Board and co-workers at Duke University for a huge water system.
4
For two functions of time f (t) and g(t) and corresponding Fourier transforms F (f) and F (g),
we define the convolution of the two original functions f and g, f ∗ g,as:f ∗g =
∞
−∞
f(τ) g(t −
τ)dτ. It can be shown that F (f ∗ g)=F (f) F (g). That is, the Fourier transform of the convolution
of two functions (f ∗ g) is just the product of the individual Fourier transforms of those functions.
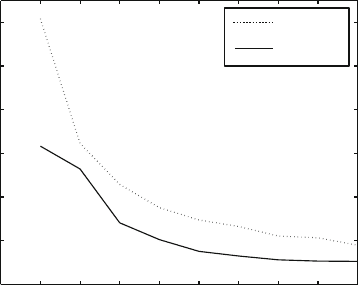
324 10. Nonbonded Computations
0 1 2 3 4 5 6 7 8 9
0
10
20
30
40
50
60
All−pairs electrostatics for 23,832 water molecules (71,496 atoms)
processors (450 MHz Pentium II)
time per timestep, sec
DPMTA
DPME
Figure 10.8. CPU time for evaluating the electrostatic energy for 23,832 water molecules
(71,496 atoms) by codes developed at Duke by John Board and co-workers for the dis-
tributed PME (DPME) and distributed parallel multipole tree algorithm (DPMTA), run at
modest accuracy of 10
−3
relative force accuracy, on a tightly coupled network of 450 MHz
Pentium II processors.
See also a review on modeling electrostatic effects in proteins [1347], which
discusses stability and accuracy issues with traditional PME, or non-spherical
Ewald methods as described above. These problems can be alleviated by using
spherical boundary conditions in combination with a local field approach. The
above review and others argue that only spherical Ewald methods rigorously give
correct results for charged systems.
10.5 The Multipole Method
In this section, we present a brief introduction to the efficient fast multipole
technique. For details, see [479,481] and other references cited below.
10.5.1 Basic Hierarchical Strategy
Fast multipole techniques are powerful alternatives to the Ewald schemes intro-
duced above for evaluating the pairwise interactions in large molecular systems.
They are widely used for many important problems in applied mathematics,
engineering, physics, chemistry, and biology [478,480]. Examples in astrophysics
include evaluation of gravitational potentials, and examples in chemistry in-
clude electrostatic potentials in molecular dynamics and quantum mechanics
(Hartree-Fock calculations).

10.5. The Multipole Method 325
Series Expansion
Multipole schemes rely on a power-series expansion that describes the interac-
tion between groups of particles (charged bodies in molecular dynamics) [1226].
The term multipole refers to the moments m
k
=
N
i=1
q
i
x
k
i
that appear in the
expansion, such as dipole and quadrupole. To see this, consider the electrostatic
potential Φ at x for unit dielectric written in terms of the charge distribution about
each atom j as (see also eqs. (10.24), (10.25) for the periodic version):
Φ(x)=Φ(x
1
, x
2
,...,x
N
)=
1
2
{i,j},i=j
q
i
q
j
/|r
ij
| =
1
2
j
q
j
Φ(x
j
) ,
(10.45)
where
Φ(x
j
)=
i=j
q
j
/|r
ij
|. (10.46)
An expansion of Φ(x
j
) yields (see Box 10.3):
Φ(x
j
)=Φ(0)+∇Φ
T
x +
1
2
x
T
Hx + O(|x|
3
) (10.47)
where the derivatives are evaluated at x =0. This expansion produces expressions
for Φ(0) based on the zeroth moment (Φ(0) = m
0
/|x
j
|), for ∇Φ(x) in terms of
the dipole moment (vector μ =[m
1
1
,m
1
2
,m
1
3
]), and for the second-derivative term
based on the quadrupole moment (elements m
2
11
,m
2
12
, m
2
13
, m
2
21
, ···,m
2
33
). See
Box 10.3 for details.
Note that multipole expansions can be expressed using Cartesian coordinations,
as in Boxes 10.3 and 10.4, or spherical coordinates, as in Subsection 10.5.3.Such
power series can save computational work since the target function can be written
as a linear combination of moments (see Box 10.4 for a simple example).
Domain Decomposition
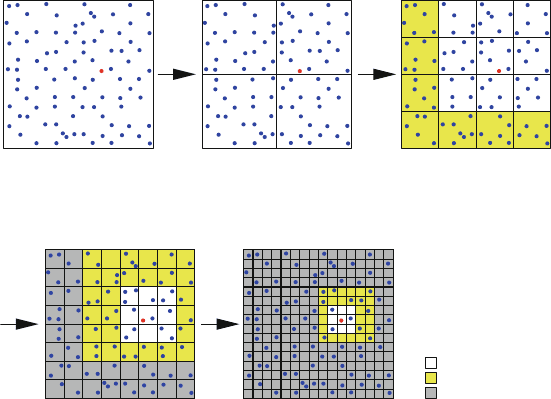
Accelerated multipole algorithms use a hierarchy of approximations to repre-
sent these interactions on the basis of a spatial particle partitioning in a tree-like
structure (typically oct-tree): the original domain (level 0) is subdivided into 8
level-1 domains, leading to 64 regions in level 2, and so on (see also illustration
in [316]). Thus, each successive refinement of the computational domain pro-
duces ‘offspring’ corresponding to the ‘parents’ at the prior level. This recursive
partitioning, like FFTs, works together with a systematic formulation and manip-
ulation of power series expansions of the target potential to reduce the evaluation
computational complexity from O(N
2
) to the more modest O(N log N ) and
O(N ), depending on the implementation (see Figure 10.9).
Multipole expansions represent one suitable choice of power series, since they
converge well when groups of particles (charges) are well-separated, allowing a
small number of coefficients in the expansions while maintaining good accuracy;
326 10. Nonbonded Computations
other expansions are possible [45,316,317,460,1329]. These power series expan-
sions are used to compute interactions between well-separated pairs (contained
in well-separated clusters). Interactions between nearby particles are computed
directly.
Summation Protocol
The various algorithms differ by how the tree structure is generated and by the
protocol used to determine which power-series approximation to invoke at ev-
ery stage (on the basis of distance separations monitored by interaction lists).
Figure 10.9, for example, illustrates the definition of interaction lists for multi-
pole expansions by boxes beyond first neighbors with respect to a given particle
(shown in red); starting from second neighbors is an alternative definition.
Generally, good efficiency — linear complexity for moderate-sized systems —
for 3D implementations requires meticulous programming and algorithmic
structure [481]. This programming sophistication is especially important for
applications where the particles are distributed heterogeneously through the com-
putational domain (usually not the case for molecular dynamics applications). For
heterogeneous cases, adaptive schemes are needed to distribute the computations
in a balanced and efficient manner since regular subdivisions may generate some
empty cells and empty cells need not be divided.
level 0: 1 box level 1: 4 boxes level 2: 16 boxes
level 3: 64 boxes level 4: 256 boxes
no well separated boxes no well separated boxes
(only near neighbors)
well separated boxes (yellow)
contribute to multipole
interaction list
previous-level multipole interactions (gray) are excluded
from multipole interaction list (yellow)
near neighbors
multipole interactions
previous interactions
Figure 10.9. Hierarchical domain partitioning approach for fast multipole schemes. The
partitioning is illustrated with respect to a central particle (shown in red).
10.5. The Multipole Method 327
The seasoned programming required for fast multiple algorithms partly ex-
plains why Ewald codes have been more popular in the molecular dynamics
community over the last few years. It is possible that as larger systems (of order
10
5
atoms) become more common in macromolecular simulations, the differ-
ence between the O(N log N) (best Ewald implementation) and O(N) (best
multipole implementation) may become significant, and the effort required for
multipole codes may well be worth the programming investment.
Besides Coulomb interactions, multipole (and Ewald) methods apply more gen-
erally to any function that can be approximated by a converging power-series
expansion, such as functions of 1/r
n
or exponentials as in screened Coulomb
(Debye-H¨uckel) expressions (exp(−κr)/r)[154,385](seebelow).
Box 10.3: Multipole Expansion
Consider a charge distribution about each atom j (in a system of N atoms) as defined in
eq. (10.46), where r
ij
= x
i
− x
j
=[x
i1
− x
j1
,x
i2
− x
j2
,x
i3
− x
j3
], r
ij
= |r
ij
|,and
R
ij
=(r
ij
)
2
. An expansion at position x about the origin can be written as
Φ(x
j
)=
N
i=1
q
i
[(x
i1
− x
j1
)
2
+(x
i2
− x
j2
)
2
+(x
i3
− x
j3
)
2
]
1/2
=Φ(0)+
N
i=1
3
k=1
∂Φ
∂x
ik
x
ik
+
1
2
N
i=1
3
l=1
3
k=1
∂
2
Φ
∂x
ik
∂x
il
x
ik
x
il
+
higher
order
terms
≡ Φ(0) + ∇Φ
T
x +
1
2
x
T
Hx + O(|x|
3
)
where derivatives are evaluated at x
i1
= x
i2
= x
i3
=0. The gradient vector ∇Φ
and Hessian matrix H above contain partial derivatives corresponding to the 3N com-
ponents of the vector x. Namely, ∇Φ has the 3N components {∂Φ/∂x
11
, ∂Φ/∂x
12
, ···,
∂Φ/∂x
N3
}, and the Hessian is:
H =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
∂
2
Φ/∂x
2
11
∂
2
Φ/∂x
11
∂x
12
...... ∂
2
Φ/∂x
11
∂x
N3
∂
2
Φ/∂x
12
∂x
11
∂
2
Φ/∂x
2
12
...... ∂
2
Φ/∂x
12
∂x
N3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
∂
2
Φ/∂x
N3
∂x
11
∂
2
Φ/∂x
N3
∂x
12
...... ∂
2
Φ/∂x
2
N3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
.
The moments {m
k
} for integers k corresponding to the partial charges {q
i
} are defined
by m
k
=
3N
i=1
q
i
x
k
i
where the summation extends over all components of x.Thefirst
term in the above expansion is written in terms of the zeroth moment m
0
:
Φ(0) =
N
i=1
q
i
[x
2
j1
+ x
2
j2
+ x
2
j3
]
1/2
=
N
i=1
q
i
|x
j
|
=
m
0
|x
j
|
.

328 10. Nonbonded Computations
The gradient, or the dipole potential, has 3 components: m
1
1
,m
1
2
,m
1
3
. They represent the
dipole moment μ. The expression for the gradient in terms of the dipole moments can be
derived following the relation for the derivatives:
∂R
−1/2
ij
∂x
ik
= −
1
2
R
−3/2
ij
∂R
ij
∂x
ik
= −r
−3
ij
(x
ik
− x
jk
)
x
ik
=0
= x
jk
/ |x
j
|
3
.
We then have:
Φ
(x
j
)=∇Φ
T
x =
N
i=1
q
i
∂R
−1/2
ij
∂x
i1
x
i1
+
∂R
−1/2
ij
∂x
i2
x
i2
+
∂R
−1/2
ij
∂x
i3
x
i3
!
=
N
i=1
q
i
x
i1
x
j1
|x
j
|
3
+ q
i
x
i2
x
j2
|x
j
|
3
+ q
i
x
i3
x
j3
|x
j
|
3
=
1
|x
j
|
3
m
1
1
x
j1
+ m
1
2
x
j2
+ m
1
3
x
j3
=
(μ
T
· x
j
)
|x
j
|
3
.
The second-derivative term, the quadrupole potential, has six terms (because of symme-
try), again with all partial derivatives evaluated at x
i1
= x
i2
= x
i3
=0:
Φ
(x
j
)=
1
2
x
T
Hx =
1
2
N
i=1
q
i
∂
2
R
−1/2
ij
∂x
2
i1
x
2
i1
+
∂
2
R
−1/2
ij
∂x
2
i2
x
2
i2
+
∂
2
R
−1/2
ij
∂x
2
i3
x
2
i3
+2
∂
2
R
−1/2
ij
∂x
i1
∂x
i2
x
i1
x
i2
+2
∂
2
R
−1/2
ij
∂x
i1
∂x
i3
x
i1
x
i3
+2
∂
2
R
−1/2
ij
∂x
i2
∂x
i3
x
i2
x
i3
!
=
1
2
m
2
11
∂
2
R
−1/2
ij
∂x
2
i1
+ m
2
22
∂
2
R
−1/2
ij
∂x
2
i2
+ ... +2m
2
23
∂
2
R
−1/2
ij
∂x
i2
∂x
i3
!
.
Box 10.4: Example of Work Reduction by Multipole Expansion
Let our potential be defined as:
Φ(x)=
N
j=1
Φ(x
j
)=
N
j=1
N
i=1
q
i
(x
j
− y
i
)
3
.
That is, Φ(x) is the sum of the following components:
{Φ(x
1
)} q
1
(x
1
− y
1
)
3
+ q
2
(x
1
− y
2
)
3
+ ... + q
N
(x
1
− y
N
)
3
{Φ(x
2
)} q
1
(x
2
− y
1
)
3
+ q
2
(x
2
− y
2
)
3
+ ... + q
N
(x
2
− y
N
)
3
.
.
.
.
.
.
.
.
.
.
.
.
{Φ(x
N
)} q
1
(x
N
− y
1
)
3
+ q
2
(x
N
− y
2
)
3
+ ... + q
N
(x
N
− y
N
)
3
.
Evaluation by straightforward summation requires O(N
2
) work, but our function of x
and y simplifies as:
(x − y)
3
= x
3
− 3x
2
y +3xy
2
− y
3
.

10.5. The Multipole Method 329
This is a finite power series, with degree p =3and moments m
k
=
N
i=1
q
i
y
k
i
. Therefore
we can rewrite each Φ(x
j
) as a linear combination of the moments {m
k
} for k =0,1,2,
3:
Φ(x
j
)=x
3
j
m
0
− 3x
2
j
m
1
+3x
j
m
2
− m
3
.
The work can thus be substantially reduced: once the moments are computed in O(Np)
work, evaluating each Φ(x
j
) requires only O(p) work, where p is the power of the
expansion, 3 here. This reduction O(N
2
) to O(3N) is significant!
10.5.2 Historical Perspective
Hierarchical Refinements
Coming from the astrophysics community, Appel first introduced the multi-
pole approach for solving the N-body problem by a hierarchical, power-series
approach [53]. Barnes and Hut accelerated the association scheme between par-
ticles at successive refinement levels to produce a method that is asymptotically
O(N log N) [90]. To see this let D
N×N
be the matrix defined by
D
ij
=
q
i
/|r
ij
| i = j
0 i = j
(10.48)
and q be the vector of N partial charges. Hence, the potential for each atom j due
to the charges induced by all other atoms is
q
j
Φ(x
j
)=q
j
i=j
q
i
/|r
ij
| = {Dq}
j
,
the jth component of the matrix/vector product Dq. Summing up the values of the
components of the resultant product (N potentials evaluated at N points) yields
the desired potential. This is clearly O(N
2
) computation by a straightforward
matrix/vector multiplication. However, if the potential Φ is sufficiently smooth
when distances are sufficiently large, the matrix D can be approximated by low-
rank submatrices; in this case, an O(Np) scheme results where p is the rank of the
approximating matrices. See also the simple example in Box 10.4 and Figure 10.9.
Hierarchical Protocol
This O(N log N) method works roughly as follows.
A hierarchy of boxes is introduced in the computational domain so that each
refinement level l is a subdivision (e.g., into 8) of the domain in level l −1.Boxes
at the same refinement level that share a boundary are considered near neighbors,
and those at the same refinement level that do not share a boundary are considered
well-separated.
As the algorithm sweeps through refinement levels, a multipole expansion is
associated with each box at that level to describe the far-field potential contribu-
tion from the particles in that box. (The clusters that contribute to this far field
