Schutz B. A first course in general relativity
Подождите немного. Документ загружается.


53 2.9 Exercises
t
(a) Show that this implies that a always has the same components in the body’s MCRF,
and that these components are what one would call ‘acceleration’ in Galilean terms.
(This would be the physical situation for a rocket whose engine always gave the
same acceleration.)
(b) Suppose a body is uniformly accelerated with α = 10 m s
−2
(about the accelera-
tion of gravity on Earth). If the body starts from rest, find its speed after time t.(Be
sure to use the correct units.) How far has it traveled in this time? How long does
it take to reach v = 0.999?
(c) Find the elapsed proper time for the body in (b), as a function of t. (Integrate dτ
along its world line.) How much proper time has elapsed by the time its speed is
v = 0.999? How much would a person accelerated as in (b) age on a trip from
Earth to the center of our Galaxy, a distance of about 2 ×10
20
m?
20 The world line of a particle is described by the equations
x(t) = at + b sin ωt, y(t) = b cos ωt,
z(t) = 0, |bω| < 1,
in some inertial frame. Describe the motion and compute the components of the
particle’s four-velocity and four-acceleration.
21 The world line of a particle is described by the parametric equations in some Lorentz
frame
t(λ) = a sinh
λ
a
, x(λ) = a cosh
λ
a
,
where λ is the parameter and a is a constant. Describe the motion and compute the
particle’s four-velocity and acceleration components. Show that λ is proper time along
the world line and that the acceleration is uniform. Interpret a.
22 (a) Find the energy, rest mass, and three-velocity v of a particle whose four-momentum
has the components (4, 1, 1, 0) kg.
(b) The collision of two particles of four-momenta
p
1
→
O
(3, −1, 0, 0) kg, p
2
→
O
(2,1,1,0)kg
results in the destruction of the two particles and the production of three new ones, two
of which have four-momenta
p
3
→
O
(1,1,0,0)kg, p
4
→
O
(1, −
1
2
,0,0)kg.
Find the four-momentum, energy, rest mass, and three-velocity of the third particle
produced. Find the CM frame’s three-velocity.
23 A particle of rest mass m has three-velocity v. Find its energy correct to terms of
order |v|
4
. At what speed |v| does the absolute value of 0(|v|
4
) term equal
1
2
of the
kinetic-energy term
1
2
m|v|
2
?
24 Prove that conservation of four-momentum forbids a reaction in which an electron and
positron annihilate and produce a single photon (γ -ray). Prove that the production of
two photons is not forbidden.

54 Vector analysis in special relativity
t
25 (a) Let frame
¯
O move with speed v in the x-direction relative to O. Let a photon have
frequency ν in O and move at an angle θ with respect to O’s x axis. Show that its
frequency in
¯
O is
¯ν/ν = (1 −v cos θ )/
√
(1 − v
2
). (2.42)
(b) Even when the motion of the photon is perpendicular to the x axis (θ = π/2) there
is a frequency shift. This is called the transverse Doppler shift, and arises because
of the time dilation. At what angle θ does the photon have to move so that there is
no Doppler shift between O and
¯
O?
(c) Use Eqs. (2.35) and (2.38) to calculate Eq. (2.42).
26 Calculate the energy that is required to accelerate a particle of rest mass m = 0from
speed v to speed v + δv (δv v), to first order in δv. Show that it would take an
infinite amount of energy to accelerate the particle to the speed of light.
27 Two identical bodies of mass 10 kg are at rest at the same temperature. One of them
is heated by the addition of 100 J of heat. Both are then subjected to the same force.
Which accelerates faster, and by how much?
28 Let
A →
O
(5, 1, −1, 0),
B →
O
(−2, 3, 1, 6),
C →
O
(2, −2, 0, 0). Let
¯
O be a frame
moving at speed v = 0.6 in the positive x direction relative to O, with its spatial axes
oriented parallel to O’s.
(a) Find the components of
A,
B, and
C in
¯
O.
(b) Form the dot products
A ·
B,
B ·
C,
A ·
C, and
C ·
C using the components in
¯
O.
Verify the frame independence of these numbers.
(c) Classify
A,
B, and
C as timelike, spacelike, or null.
29 Prove, using the component expressions, Eqs. (2.24) and (2.26), that
d
dτ
(
U ·
U) = 2
U ·
d
U
dτ
.
30 The four-velocity of a rocket ship is
U →
O
(2, 1, 1, 1). It encounters a high-velocity
cosmic ray whose momentum is
P →
O
(300, 299, 0, 0) × 10
−27
kg. Compute the
energy of the cosmic ray as measured by the rocket ship’s passengers, using each of
the two following methods.
(a) Find the Lorentz transformations from O to the MCRF of the rocket ship, and use
it to transform the components of
P.
(b) Use Eq. (2.35).
(c) Which method is quicker? Why?
31 A photon of frequency ν is reflected without change of frequency from a mirror, with
an angle of incidence θ . Calculate the momentum transferred to the mirror. What
momentum would be transferred if the photon were absorbed rather than reflected?
32 Let a particle of charge e and rest mass m, initially at rest in the laboratory, scatter
a photon of initial frequency ν
i
. This is called Compton scattering. Suppose the scat-
tered photon comes off at an angle θ from the incident direction. Use conservation of
four-momentum to deduce that the photon’s final frequency ν
f
is given by

55 2.9 Exercises
t
1
ν
f
=
1
ν
i
+ h
1 − cos θ
m
. (2.43)
33 Space is filled with cosmic rays (high-energy protons) and the cosmic microwave back-
ground radiation. These can Compton scatter off one another. Suppose a photon of
energy hν = 2 × 10
−4
eV scatters off a proton of energy 10
9
m
P
= 10
18
eV, energies
measured in the Sun’s rest frame. Use Eq. (2.43) in the proton’s initial rest frame to
calculate the maximum final energy the photon can have in the solar rest frame after
the scattering. What energy range is this (X-ray, visible, etc.)?
34 Show that, if
A,
B, and
C are any vectors and α and β any real numbers,
(α
A) ·
B = α(
A ·
B),
A · (β
B) = β(
A ·
B),
A · (
B +
C) =
A ·
B +
A ·
C,
(
A +
B) ·
C =
A ·
C +
B ·
C.
35 Sho
w that the vectors {e
¯
β
} obtained from {e
α
} by Eq. (2.15) satisfy e
¯α
·e
¯
β
= η
¯α
¯
β
for
all ¯α,
¯
β.

3 Tensor analysis in special relativity
3.1 T h e m et ri c t en s or
Consider the representation of two vectors
A and
B on the basis {e
α
} of some frame O :
A = A
α
e
α
,
B = B
β
e
β
.
Their scalar product is
A ·
B = (A
α
e
α
) · (B
β
e
β
).
(Note the importance of using different indices α and β to distinguish the first summation
from the second.) Following Exer. 34, § 2.9, we can rewrite this as
A ·
B = A
α
B
β
(e
α
·e
β
),
which, by Eq. (2.27), is
A ·
B = A
α
B
β
η
αβ
. (3.1)
This is a frame-invariant way of writing
−A
0
B
0
+ A
1
B
1
+ A
2
B
2
+ A
3
B
3
.
The numbers η
αβ
are called ‘components of the metric tensor’. We will justify this name
later. Right now we observe that they essentially give a ‘rule’ for associating with two
vectors
A and
B a single number, which we call their scalar product. The rule is that the
number is the double sum A
α
B
β
η
αβ
. Such a rule is at the heart of the meaning of ‘tensor’,
as we now discuss.
3.2 Definition of tensors
We make the following definition of a tensor:
A tensor of type
0
N
is a function of N vectors into the real numbers, which is linear in each of its N
arguments.

57 3.2 Definition of tensors
t
Let us see what this definition means. For the moment, we will just accept the notation
0
N
;
its justification will come later in this chapter. The rule for the scalar product, Eq. (3.1),
satisfies our definition of a
0
2
tensor. It is a rule which takes two vectors,
A and
B, and
produces a single real number
A ·
B. To say that it is linear in its arguments means what is
proved in Exer. 34, § 2.9. Linearity on the first argument means
(α
A) ·
B = α(
A ·
B),
and
(
A +
B) ·
C =
A ·
C +
B ·
C,
⎫
⎬
⎭
(3.2)
while linearity on the second argument means
A · (β
B) = β(
A ·
B),
A · (
B +
C) =
A ·
B +
A ·
C.
This
definition of linearity is of central importance for tensor algebra, and the student
should study it carefully.
To give concreteness to this notion of the dot product being a tensor, we introduce a
name and notation for it. We let g be the metric tensor and write, by definition,
g(
A,
B):=
A ·
B. (3.3)
Then we regard g( , ) as a function which can take two arguments, and which is linear
in that
g(α
A + β
B,
C) = α g(
A,
C) +β g(
B,
C), (3.4)
and similarly for the second argument. The value of g on two arguments, denoted by
g(
A,
B), is their dot product, a real number.
Notice that the definition of a tensor does not mention components of the vectors. A
tensor must be a rule which gives the same real number independently of the reference
frame in which the vectors’ components are calculated. We showed in the previous chapter
that Eq. (3.1) satisfies this requirement. This enables us to regard a tensor as a function of
the vectors themselves rather than of their components, and this can sometimes be helpful
conceptually.
Notice that an ordinary function of position, f (t, x, y, z), is a real-valued function of no
vectors at all. It is therefore classified as a
0
0
tensor.
Aside on the usage of the term ‘function’
The most familiar notion of a function is expressed in the equation
y = f (x),
where y and x are real numbers. But this can be written more precisely as: f is a ‘rule’
(called a mapping) which associates a real number (symbolically called y, above) with
another real number, which is the argument of f (symbolically called x, above). The func-
tion itself is not f (x), since f (x)isy, which is a real number called the ‘value’ of the
58 Tensor analysis in special relativity
t
function. The function itself is f , which we can write as f ( ) in order to show that it has
one argument. In algebra this seems like hair-splitting since we unconsciously think of x
and y as two things at once: they are, on the one hand, specific real numbers and, on the
other hand, names for general and arbitrary real numbers. In tensor calculus we will make
this distinction explicit:
A and
B are specific vectors,
A ·
B is a specific real number, and g
is the name of the function that associates
A ·
B with
A and
B.
Components of a tensor
Just like a vector, a tensor has components. They are defined as:
The components in a frame O of a tensor of type
0
N
are the values of the function when its arguments
are the basis vectors {e
α
} of the frame O.
Thus we have the notion of components as frame-dependent numbers (frame-dependent
because the basis refers to a specific frame). For the metric tensor, this gives the
components as
g(e
α
, e
β
) =e
α
·e
β
= η
αβ
. (3.5)
So the matrix η
αβ
that we introduced before is to be thought of as an array of the compo-
nents of g on the basis. In another basis, the components could be different. We will have
many more examples of this later. First we study a particularly important class of tensors.
3.3 T h e
0
1
tensors: one-forms
A tensor of the type
0
1
is called a covector, a covariant vector, or a one-form. Often these
names are used interchangeably, even in a single text-book or reference.
General properties
Let an arbitrary one-form be called ˜p. (We adopt the notation that ˜ above a symbol denotes
a one-form, just as above a symbol denotes a vector.) Then ˜p, supplied with one vector
argument, gives a real number: ˜p(
A) is a real number. Suppose ˜q is another one-form. Then
we can define
˜s =˜p +˜q,
˜r = α ˜p,
(3.6a)

59 3.3 The
0
1
tensors: one-forms
t
to be the one-forms that take the following values for an argument
A:
˜s(
A) =˜p(
A) +q(
A),
˜r(
˜
A) = αp(
A).
(3.6b)
With these rules, the set of all one-forms satisfies the axioms for a vector space, which
accounts for their other names. This space is called the ‘dual vector space’ to distinguish it
from the space of all vectors such as
A.
When discussing vectors we relied heavily on components and their transformations.
Let us look at those of ˜p. The components of ˜p are called p
α
:
p
α
:=˜p(e
α
). (3.7)
Any component with a single lower index is, by convention, the component of a one-form;
an upper index denotes the component of a vector. In terms of components, ˜p(
A)is
˜p(
A) =˜p(A
α
e
α
)
= A
α
˜p(e
α
),
˜p(
A) = A
α
p
α
. (3.8)
The second step follows from the linearity which is the heart of the definition we gave of a
tensor. So the real number ˜p(
A) is easily found to be the sum A
0
p
0
+ A
1
p
1
+ A
2
p
2
+ A
3
p
3
.
Notice that all terms have plus signs: this operation is called contraction of
A and ˜p, and
is more fundamental in tensor analysis than the scalar product because it can be performed
between any one-form and vector without reference to other tensors. We have seen that
two vectors cannot make a scalar (their dot product) without the help of a third tensor, the
metric.
The components of ˜p on a basis {e
¯
β
} are
p
¯
β
:=˜p(e
¯
β
) =˜p(
α
¯
β
e
α
)
=
α
¯
β
˜p(e
α
) =
α
¯
β
p
α
. (3.9)
Comparing this with
e
¯
β
=
α
¯
β
e
α
,
we see that components of one-forms transform in exactly the same manner as basis vectors
and in the opposite manner to components of vectors. By ‘opposite’, we mean using the
inverse transformation. This use of the inverse guarantees that A
α
p
α
is frame independent
for any vector
A and one-form ˜p. This is such an important observation that we shall prove
it explicitly:
A
¯α
p
¯α
= (
¯α
β
A
β
)(
μ
¯α
p
μ
), (3.10a)
=
μ
¯α
¯α
β
A
β
p
μ
, (3.10b)
= δ
μ
β
A
β
p
μ
, (3.10c)
= A
β
p
β
. (3.10d)

60 Tensor analysis in special relativity
t
(This is the same way in which the vector A
α
e
α
is kept frame independent.) This inverse
transformation gives rise to the word ‘dual’ in ‘dual vector space’. The property of trans-
forming with basis vectors gives rise to the co in ‘covariant vector’ and its shorter form
‘covector’. Since components of ordinary vectors transform oppositely to basis vectors (in
order to keep A
β
e
β
frame independent), they are often called ‘contravariant’ vectors. Most
of these names are old-fashioned; ‘vectors’ and ‘dual vectors’ or ‘one-forms’ are the mod-
ern names. The reason that ‘co’ and ‘contra’ have been abandoned is that they mix up
two very different things: the transformation of a basis is the expression of new vectors in
terms of old ones; the transformation of components is the expression of the same object in
terms of the new basis. It is important for the student to be sure of these distinctions before
proceeding further.
Basis one-forms
Since the set of all one-forms is a vector space, we can use any set of four linearly inde-
pendent one-forms as a basis. (As with any vector space, one-forms are said to be linearly
independent if no nontrivial linear combination equals the zero one-form. The zero one-
form is the one whose value on any vector is zero.) However, in the previous section we
have already used the basis vectors {e
α
} to define the components of a one-form. This sug-
gests that we should be able to use the basis vectors to define an associated one-form basis
{˜ω
α
, α = 0, ...,3}, which we shall call the basis dual to {e
α
}, upon which a one-form has
the components defined above. That is, we want a set {˜ω
α
} such that
˜p = p
α
˜ω
α
. (3.11)
(Notice that using a raised index on ˜ω
α
permits the summation convention to operate.) The
{˜ω
α
} are four distinct one-forms, just as the {e
α
} are four distinct vectors. This equation
must imply Eq. (3.8) for any vector
A and one-form ˜p:
˜p(
A) = p
α
A
α
.
But from Eq. (3.11) we get
˜p(
A) = p
α
˜ω
α
(
A)
= p
α
˜ω
α
(A
β
e
β
)
= p
α
A
β
˜ω
α
(e
β
).
(Notice the use of β as an index in the second line, in order to distinguish its summation
from the one on α.) Now, this final line can only equal p
α
A
α
for all A
β
and p
α
if
˜ω
α
(e
β
) = δ
α
β
. (3.12)
Comparing with Eq. (3.7), we see that this equation gives the βth component of the
αth basis one-form. It therefore defines the αth basis one-form. We can write out these
components as

61 3.3 The
0
1
tensors: one-forms
t
˜ω
0
→
O
(1,0,0,0),
˜ω
1
→
O
(0,1,0,0),
˜ω
2
→
O
(0,0,1,0),
˜ω
3
→
O
(0,0,0,1).
It is important to understand two points here. One is that Eq. (3.12) defines the basis
{˜ω
α
} in terms of the basis {e
β
}. The vector basis induces a unique and convenient one-
form basis. This is not the only possible one-form basis, but it is so useful to have the
relationship, Eq. (3.12), between the bases that we will always use it. The relationship,
Eq. (3.12), is between the two bases, not between individual pairs, such as ˜ω
0
and e
0
.
That is, if we change e
0
, while leaving e
1
, e
2
, and e
3
unchanged, then in general this
induces changes not only in ˜ω
0
but also in ˜ω
1
, ˜ω
2
, and ˜ω
3
. The second point to under-
stand is that, although we can describe both vectors and one-forms by giving a set of four
components, their geometrical significance is very different. The student should not lose
sight of the fact that the components tell only part of the story. The basis contains the
rest of the information. That is, a set of numbers (0, 2, −1, 5) alone does not define any-
thing; to make it into something, we must say whether these are components on a vector
basis or a one-form basis and, indeed, which of the infinite number of possible bases is
being used.
It remains to determine how {˜ω
α
}transforms under a change of basis. That is, each frame
has its own unique set {˜ω
α
}; how are those of two frames related? The derivation here is
analogous to that for the basis vectors. It leads to the only equation we can write down with
the indices in their correct positions:
˜ω
¯α
=
¯α
β
˜ω
β
. (3.13)
This is the same as for components of a vector, and opposite that for components of a
one-form.
Picture of a one-form
For vectors we usually imagine an arrow if we need a picture. It is helpful to have an
image of a one-form as well. First of all, it is not an arrow. Its picture must reflect the
fact that it maps vectors into real numbers. A vector itself does not automatically map
another vector into a real number. To do this it needs a metric tensor to define the scalar
product. With a different metric, the same two vectors will produce a different scalar prod-
uct. So two vectors by themselves don’t give a number. We need a picture of a one-form
which doesn’t depend on any other tensors having been defined. The one generally used
by mathematicians is shown in Fig. 3.1. The one-form consists of a series of surfaces. The
‘magnitude’ of it is given by the spacing between the surfaces: the larger the spacing the
smaller the magnitude. In this picture, the number produced when a one-form acts on a
vector is the number of surfaces that the arrow of the vector pierces. So the closer their
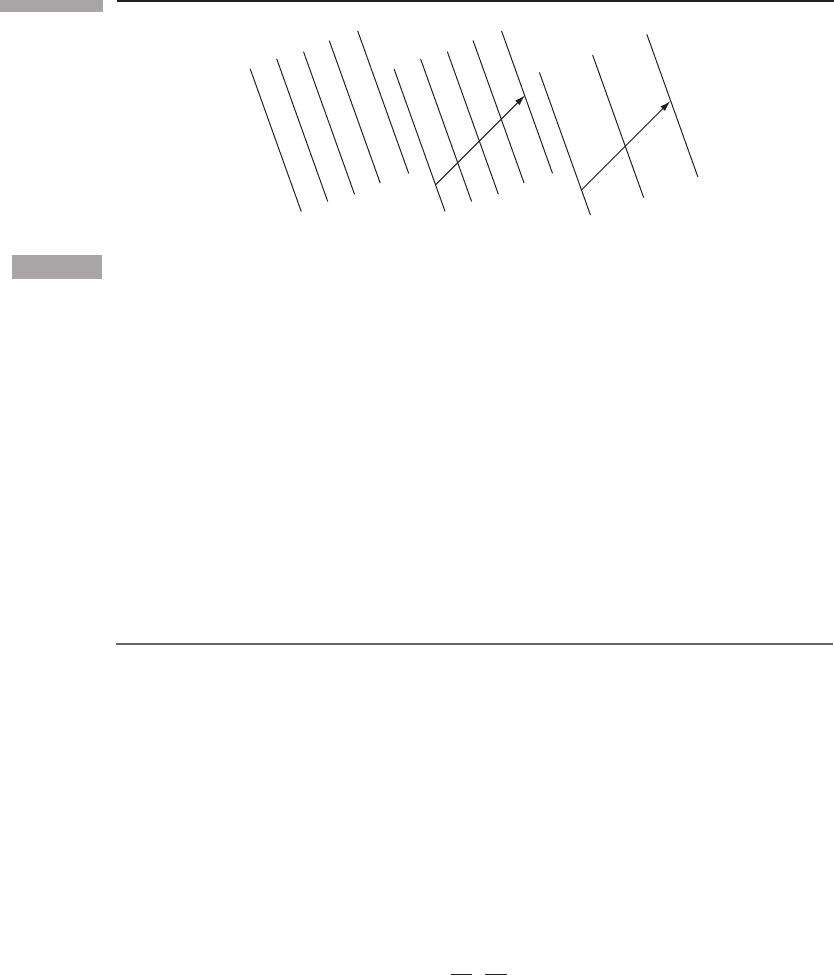
62 Tensor analysis in special relativity
t
(a) (b) (c)
t
Figure 3.1
(a) The picture of one-form complementary to that of a vector as an arrow. (b) The value of a
one-form on a given vector is the number of surfaces the arrow pierces. (c) The value of a smaller
one-form on the same vector is a smaller number of surfaces. The larger the one-form, the more
‘intense’ the slicing of space in its picture.
spacing, the larger the number (compare (b) and (c)inFig.3.1). In a four-dimensional
space, the surfaces are three-dimensional. The one-form doesn’t define a unique direction,
since it is not a vector. Rather, it defines a way of ‘slicing’ the space. In order to justify this
picture we shall look at a particular one-form, the gradient.
Gradient of a function is a one-form
Consider a scalar field φ(x) defined at every event x. The world line of some particle (or
person) encounters a value of φ at each on it (see Fig. 3.2), and this value changes from
event to event. If we label (parametrize) each point on the curve by the value of proper
time τ along it (i.e. the reading of a clock moving on the line), then we can express the
coordinates of events on the curve as functions of τ:
[t = t(τ ), x = x(τ ), y = y(τ ), z = z(τ )].
The four-velocity has components
U →
d t
dτ
,
d x
dτ
, ...
.
Since φ is a function of t, x, y, and z, it is implicitly a function of τ on the curve:
φ(τ ) = φ[t(τ ), x(τ ), y(τ ), z(τ )],
and its rate of change on the curve is
