Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

12.2. ОПЕРАЦИИ НАД СЛУЧАЙНОЙ ВЕЛИЧИНОЙ

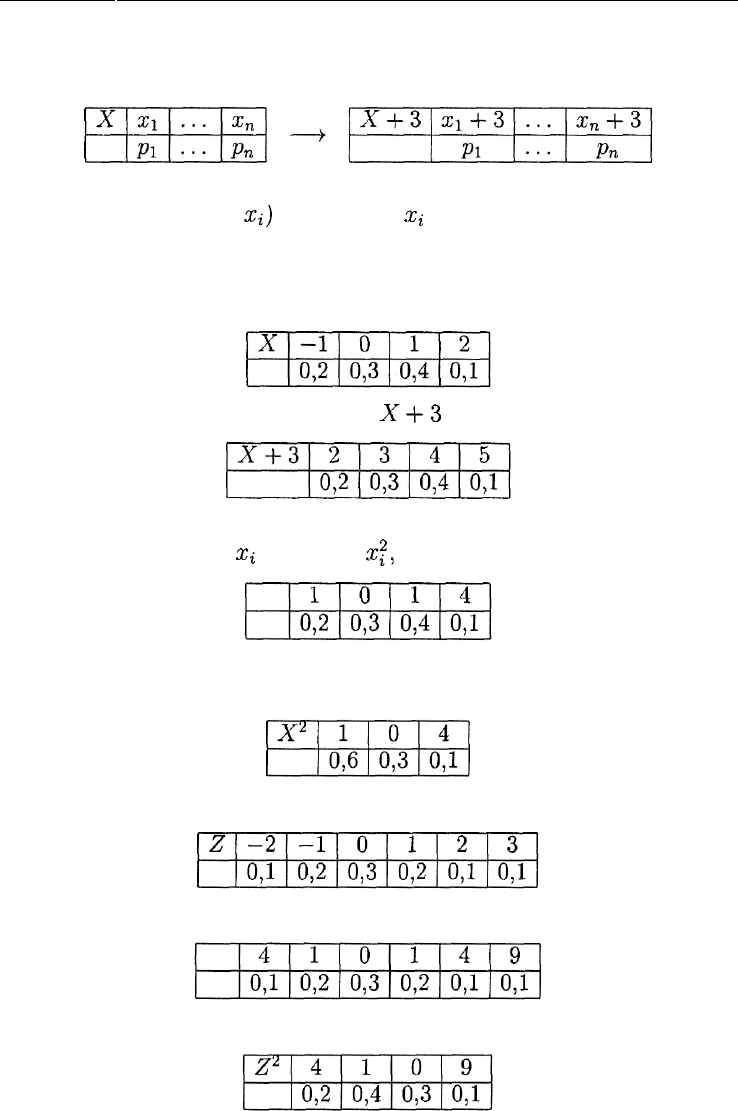
Таблица распределения случайной величины Х + 3 строится по

таблице распределения случайной величины X следующим образом:

Как видно, вторая строка осталась без изменений, поскольку веро-

ятности событий {X =

%i)

и (X + 3 =

+ 3) равны.

Построение таблицы распределения случайной величины X

не-

сколько сложнее.

Рассмотрим конкретный пример:

Таблица для случайной величины

строится просто:

Пытаясь действовать аналогичным образом для величины X

, т. е.

заменяя все значения

Х{

числами

xf,

получаем:

В первой строке есть совпадающие значения. Поэтому следует объ-

единить их в одно, сложив соответствующие вероятности:

Рассмотрим еще один пример:

Возводя значения случайной величины Z в квадрат, получаем:

И наконец, в результате имеем:

241

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Таблицу распределения случайной величины Y = f(X) для лю-

бой функции / можно построить аналогично. Она строится в два

этапа. Сначала вычисляются элементы вспомогательной таблицы

Затем совпадающие значения

f(xi)

f{xj)

для

разных чисел

ж,

(если такие имеются) объединяются в одно, а соответствующие

вероятности складываются.

12.3. Числовые характеристики

случайной

величины

Как было отмечено ранее, случайная величина полностью определя-

ется своим законом распределения. При этом закон распределения

может быть задан, например, при помощи таблицы распределения.

Однако во многих практических задачах (в том числе в задачах при-

нятия решения) требуется представить информацию о случайной

величине в более компактном, обозримом виде. Обычно для этого

применяются так называемые числовые характеристики случайной

величины — числа, на основании которых можно судить об интере-

сующих нас факторах.

Приведем пример. Пусть имеются две альтернативные стратегии

действий, каждая из которых обещает принести определенную при-

быль, причем в обоих случаях прибыль зависит от различных слу-

чайных обстоятельств и в силу этого является случайной величи-

ной. Законы распределения обеих случайных величин будем считать

известными (заданными в виде таблиц). Какую стратегию следует

предпочесть?

Ниже мы рассмотрим две числовые характеристики случайной

величины, позволяющие в ситуациях такого рода принимать доста-

точно обоснованное решение.

Математическое ожидание

Первая важная характеристика — это среднее ожидаемое значение,

принимаемое случайной величиной в больших сериях испытаний.

242

12.3.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

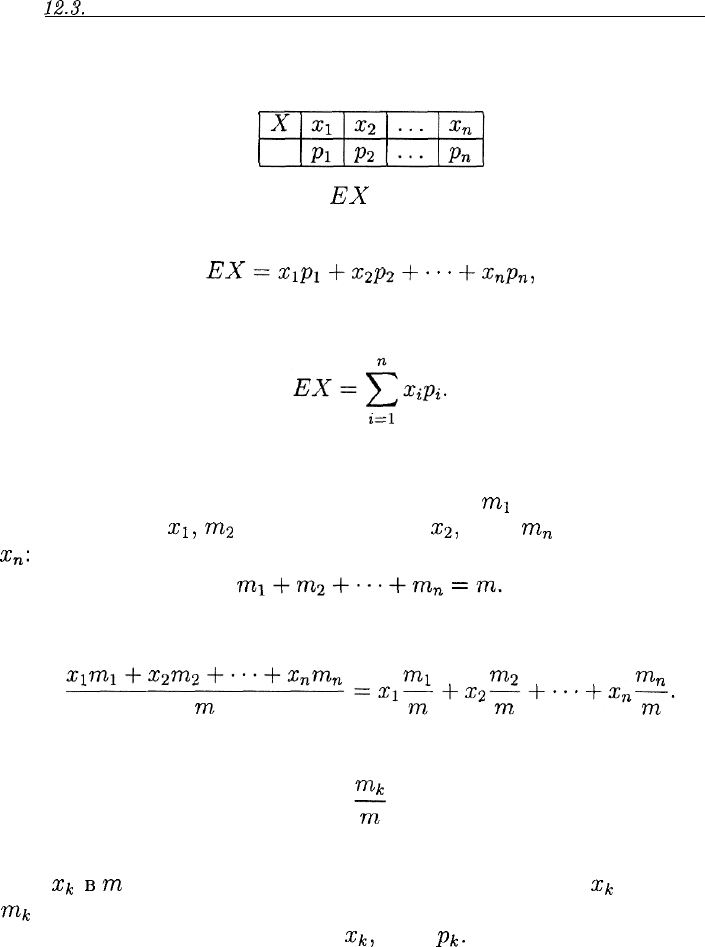
Пусть имеется случайная величина X с заданной таблицей рас-

пределения

Математическое ожидание

(ср. англ. expectation) случайной

величины X определяется формулой

которая в сокращенной записи выглядит так:

Поясним эту формулу. Предположим, что проведено т испытаний

(т — достаточно большое число), при этом

т\

раз величина X при-

няла значение

х\,

раза — значение

... ,

тп

раз — значение

Найдем среднее арифметическое всех этих m значений. Имеем:

Дробь

представляет собой относительную частоту появления события

X =

х^

вт

испытаниях (в т испытаниях событие X =

х^

произошло

rrik

раз). При больших значениях т относительная частота примерно

равна вероятности события X =

Хк,

т. е.

Pk-

Во многих случаях альтернативы можно сравнивать на основании

средних значений. Особенно это оправданно тогда, когда решение

приходится принимать в однотипных ситуациях много раз, т. е. фа-

ктически проводить большое число испытаний (например, магазин

каждый день решает, сколько батонов хлеба закупить для реализа-

ции в течение следующего дня).

243

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Пример

Предприниматель размышляет над тем, куда лучше

вложить деньги — в киоск для торговли мороженым или в палатку

для торговли хлебобулочными изделиями.

Вложение средств в киоск с вероятностью 0,5 обеспечит годовую

прибыль 5 тыс. долл., с вероятностью 0,2 — 10 тыс. долл. и с веро-

ятностью 0,3 — 3 тыс. долл.

Для палатки прогноз таков: 5,5 тыс. долл. — с вероятностью 0,6,

5 тыс. долл. — с

вероятностью

0,3 и 6,5 тыс. долл. — с вероятностью

0,1.

В каком случае (для киоска или для палатки) математическое

ожидание годового дохода больше?

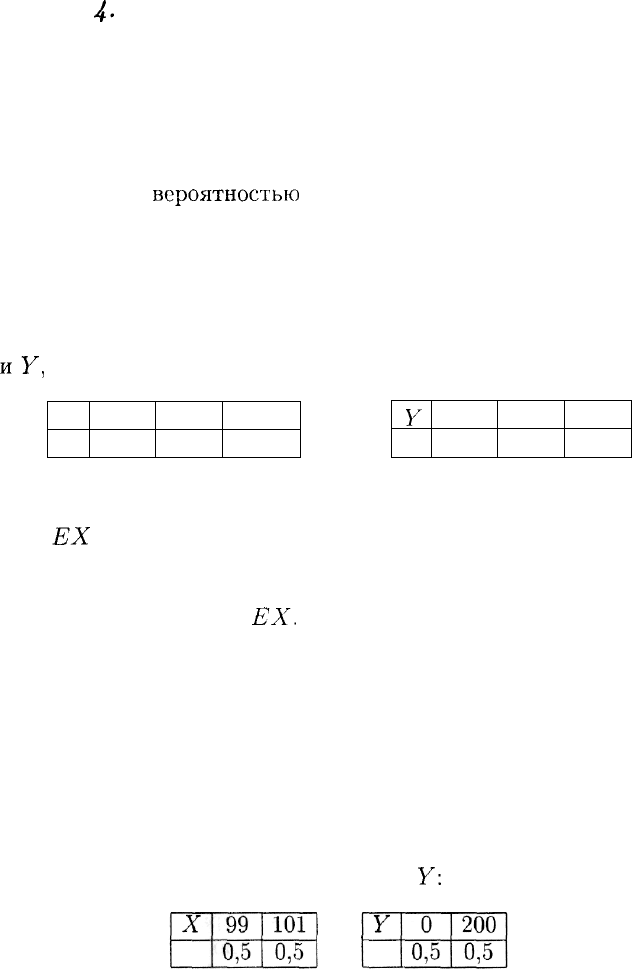
Решение. Для каждого из двух возможных решений годовая при-

быль является случайной величиной. Обозначив эти величины через

иУ,

построим таблицы распределения:

3000

0,3

5000

0,5

10000

0,2

5000

0,3

5500

0,6

6500

0,1

Найдем математические ожидания:

ЕХ

= 3000 • 0,3 + 5000 • 0,5 + 10000 • 0,2 = 5400 долл.,

ЕУ = 5000 • 0,3 + 5500 • 0,6 + 6500 • 0,1 = 5450 долл.

Получается, что ЕУ >

ЕХ.

Таким образом, математическое ожи-

дание для палатки больше.

Дисперсия и стандартное отклонение

Итак, математическое ожидание определяет, какое значение случай-

ная величина принимает "в среднем". Следующий простейший при-

мер показывает, что случайные величины с равным математическим

ожиданием могут существенно различаться по степени близости к

нему.

Рассмотрим случайные величины X и

У:

(1)

Нетрудно видеть, что ЕХ — ЕУ = 100. Но если для величины X

отклонение от значения 100 незначительно, то для величины У оно

весьма заметно.

244

12.3.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Если выбор между величинами X и Y — это выбор между двумя

альтернативными решениями, то X — это стабильная, предсказуе-

мая прибыль, а

— это риск. Считается, что при принятии решений

в большинстве случаев пытаются уменьшить непредсказуемость, по-

казателем которой является степень отклонения случайной вели-

чины от ее математического ожидания. Для измерения этого по-

казателя применяется еще одна числовая характеристика случай-

ной величины, называемая дисперсией. Обозначение: DX (ср. англ.

dispersion). Покажем, как она вычисляется.

Вычитая из случайной величины X ее математическое ожидание,

получаем новую случайную величину

Квадрат последней также является случайной величиной

математическое ожидание которой и есть дисперсия:

Если величина X задана таблицей

то дисперсия случайной величины X может быть вычислена по

формуле

или более просто:

Пример 5. Вычислим дисперсии случайных величин X и Y, та-

блицы которых приведены выше — см. (1):

245

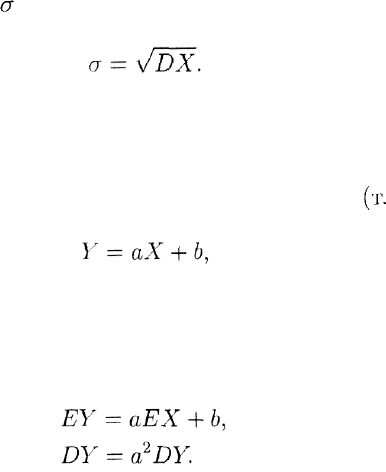
ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Пример 6. Для биномиальной случайной величины X =

= Bi(n,p) справедливы соотношения

Замечание. Математическое ожидание может быть любым числом,

а дисперсия всегда неотрицательна.

Случайные величины, моделирующие какие-либо объекты реаль-

ного мира, обычно имеют размерность. Это означает, что принима-

емые ими значения могут измеряться в штуках, метрах, килограм-

мах и т. п. При этом математическое ожидание случайной величины

имеет ту же размерность, что и сама случайная величина. Размер-

ность же дисперсии равна квадрату размерности случайной величи-

ны. Например, если случайная величина измеряется в рублях, то ее

дисперсия — в рублях в квадрате.

Чтобы не иметь дело с такими причудливыми единицами измере-

ния, вводится понятие стандартного отклонения. Оно обозначает-

ся греческой буквой

(сигма) и по определению равно квадратному

корню из дисперсии

Тем самым, стандартное отклонение имеет ту же размерность, что

и сама случайная величина.

Выше шла речь об операциях над случайными величинами. В слу-

чае линейных преобразований случайной величины X

(т.

е. преобра-

зований вида

где а и b — некоторые числа) математическое ожидание и дисперсию

получившейся случайной величины Y можно вычислить, исходя из

этих же числовых характеристик величины X. Именно, справедливы

следующие формулы:

Стандартная случайная величина

Случайная величина, у которой математическое ожидание равно О,

а дисперсия равна 1, называется стандартной.

246

12.4. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ С БЕСКОНЕЧНЫМ ЧИСЛОМ ЗНА ЧЕНИЙ

Пусть имеется случайная величина X с математическим ожида-

нием

(мю) и стандартным отклонением

а.

Нетрудно показать, что

случайная величина

является стандартной.

12.4.

Случайные

величины

с бесконечным числом значений

Выше мы рассматривали случайные величины, принимающие ко-

нечное число значений. Однако часто возникает необходимость рас-

смотрения случайных величин, число возможных значений которых

бесконечно.

Приведем два простых примера.

Пример

7. Испытание состоит в бросании монеты до первого

выпадания герба. Случайная величина

— количество бросаний —

может принимать значения 1, 2, 3 и так далее, т. е. бесконечное число

значений.

Пример 8. Испытание состоит в том, что на отрезке [0;1] число-

вой оси случайным образом отмечается точка (изначально все точки

отрезка "равноправны", т. е. шансы каждой точки быть отмеченной

такие же, как у любой другой). Случайная величина X — число от-

резка [0;1], соответствующее отмеченной точке, — может принимать

любые значения из отрезка [0;1].

Натуральных чисел, равно как и точек отрезка [0;1], бесконечно

много. Однако на числовой прямой они расположены изолированно

друг от друга (дискретно). Отмеченное свойство объединяет вели-

чину

из примера 7 со случайными величинами, принимающими

конечное число значений. Все эти величины называются дискрет-

ными случайными величинами.

Для случайной величины Y из примера 7 можно построить "бес-

конечную таблицу распределения" следующего вида:

В отличие от дискретных случайных величин случайная величи-

на X из примера 8 является непрерывной случайной величиной —

247

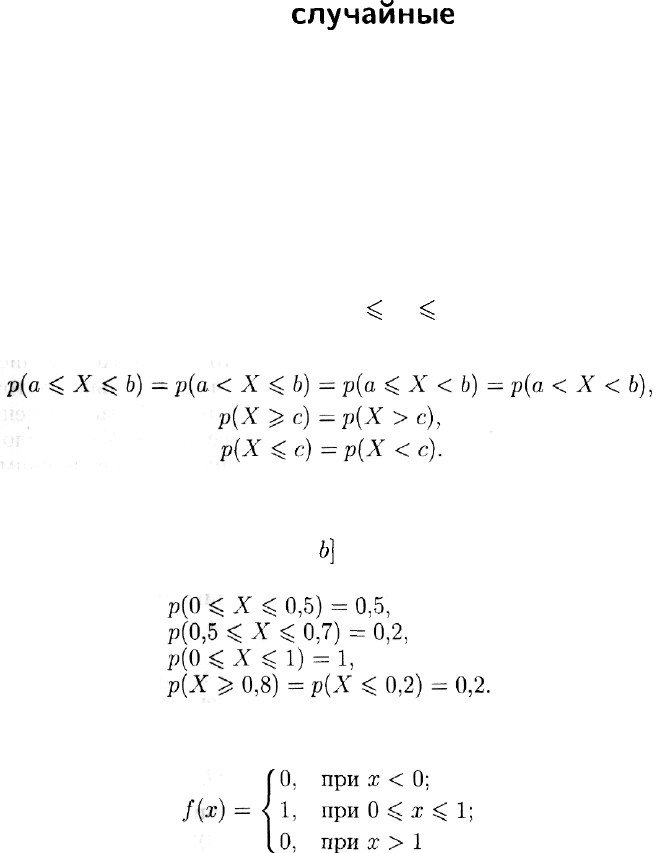
ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

точки отрезка [0;1] нельзя одну за другой выделить и записать в

таблицу (хотя бы и бесконечную).

Существуют еще случайные величины смешанного типа.

Далее мы будем рассматривать только случайные величины, при-

нимающие конечное число значений, и непрерывные случайные ве-

личины.

12.5. Непрерывные

случайные

величины

Под непрерывной случайной величиной мы будем понимать случай-

ную величину, принимающую значения на прямой, луче (полупря-

мой) или отрезке. Описание закона распределения в непрерывном

случае существенно сложнее, чем в дискретном.

Главное различие в задачах вычисления вероятностей для дис-

кретного и непрерывного случаев состоит в следующем. В дискрет-

ном случае ищется вероятность событий типа X = с (случайная

величина принимает определенное значение). В непрерывном слу-

чае вероятности такого типа равны нулю, поэтому интерес предста-

вляют вероятности событий типа а ^ X ^ b (случайная величина

принимает значения из некоторого отрезка). При этом

Для случайной величины X, с равной вероятностью принимаю-

щей любое значение из отрезка [0;1], естественно считать, что веро-

ятность попадания в отрезок [а;

Ь]

равна длине этого отрезка. На-

пример,

Рассмотрим функцию

248

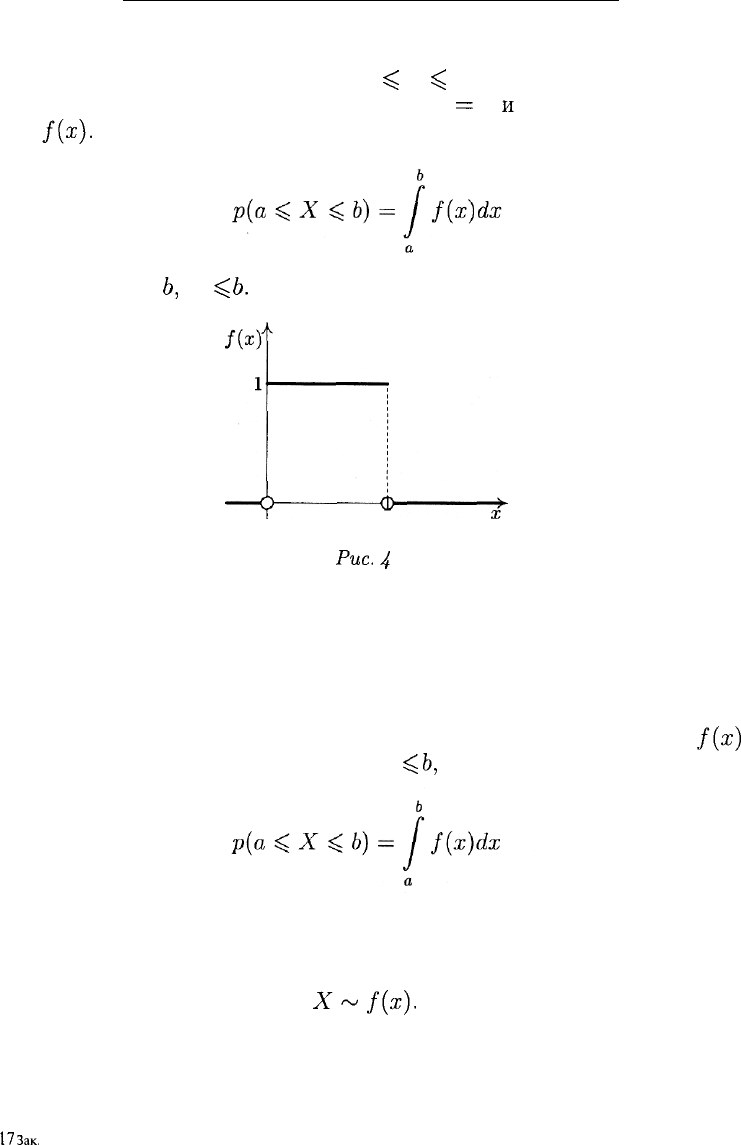
12.5. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

(рис. 4). Ее связывает со случайной величиной X следующее обсто-

ятельство: вероятность события а ^ X ^ b равна площади фигуры,

ограниченной прямыми у = 0, х = а, х

графиком функции

у =

f(x).

Иными словами, справедливо равенство

для любых а и

Ь,

а ^

Ь.

Рис.

Таким образом, функция f(x) позволяет вычислять вероятности,

связанные со случайной величиной X, т. е., по сути, задает закон

распределения случайной величины X.

Посмотрим теперь на ситуацию с более общей точки зрения. Пусть

имеется случайная величина X и неотрицательная функция

f(x)

такая, что для любых чисел а и b, a ^

выполняется равенство

(рис. 5). В этом случае говорят, что случайная величина X имеет

плотность распределения f(x). Записывается это следующим обра-

зом:

X~f{x).

Замечание 1. Интеграл от плотности распределения по всей области

возможных значений случайной величины равен 1.

Зак.

7492

249

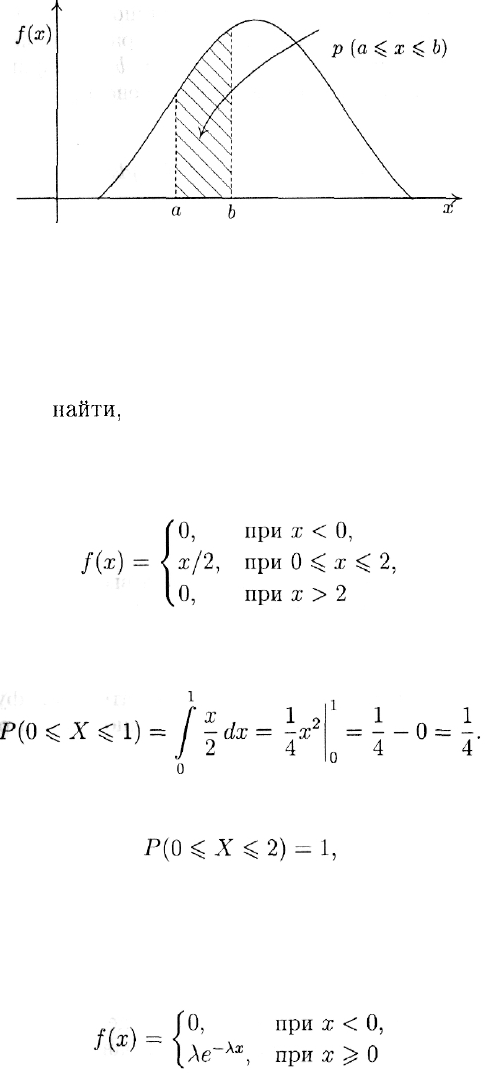
ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Рис. 5

Замечание 2. Описанная ситуация допускает следующую аналогию

из механики. Пусть имеется сплошной стержень массой 1 кг. Масса

распределена по стержню с различной, вообще говоря, плотностью.

Если мы хотим

найти,

сколько весит некоторый отрезок стержня,

надо взять по этому отрезку интеграл от плотности.

Пример 9. Пусть случайная величина X задана плотностью

распределения

(рис. 6). Для нахождения вероятностей требуется вычислять соот-

ветствующие интегралы. Например:

Важно отметить, что

поскольку все возможные значения величины X лежат в пределах

от 0 до 2.

Пример 10. Показательное (экспоненциальное) распределение

задается плотностью вида

250