Шимбирев Б.П. Теория фигуры Земли
Подождите немного. Документ загружается.


каждую из производных множат на зт 0 в степени, равной порядку произ-
водной.
Полученные, таким образом, присоединенные функции Лежандра множат
на синус и косинус кратности долготы А, равной порядку взятой производной.
Проиллюстрируем эти правила на примерах.
Положив в (111.27) п = 1, получим присоединенную функцию Лежандра
г> • ъ п Л
к
соз 0
Р
1к
=
81П
0 г- .
(а соз 0)"
При к = 1 Р
п
= зт 0. Присоединенные функции первого порядка будут
зт 0 соз
А,
и зтОзтА.
Положив в (111.27) п = 2, получим
'(|СО320 П
Р
2А = 8
111*0—11
(а соз
0)
к
Полагая к = 1 и 2, получим соответственно Р
21
= 3 зт 0-соз 0 и Р
22
=
= 3 зт
2
0. Следовательно, присоединенные функции будут иметь вид
3 зт 0 соз 0 соз
А,
3 зт 0 соз
0
зт
А,
3 зт
2
0 соз 2А и 3 зт
2
0 вт 2А.
Поскольку разложением в ряд по сферическим функциям приходится
пользоваться довольно часто, приведем значения сферических функ-
ций Р
п0
и Р
пк
до пятой степени включительно в табл. 1.
§ 17. НОРМИРОВАНИЕ СФЕРИЧЕСКИХ ФУНКЦИЙ
Во многих работах вместо обычных сферических функций используют
нормированные сферические функции, отличающиеся от обычных лишь постоян-
ными множителями. Эти множители подбирают таким образом, чтобы достичь
известной симметрии основных формул.
Так, например, если положить
РпьФ) = дпкРпьФ), где д
пк
=
(гс —
к)
!
(п +
к)
! '
Р„(соз0) = Р
п
(соз0), д
по
=1.
то интегралы от квадратов всех (2п + 1) сферических функций, взятые по еди-
ничной сфере, будут равны одной и той же величине 4я/(2п 4- 1), т. е.
со
Если разложение по сферическим функциям представить рядом
/(6, А) = 2 2 {А
пк
созк% + В
пк
8шкХ)Р
пк
ф),
п=о
к=О
80

то коэффициенты ряда определятся по формулам
А
пк
= ^5 / (0", Я,')Р
пА
(0") соз кХ' йсо;
со
В
пк
= ЭД /(0', А') (0')зт ЛЛ' А*.
со
Разумеется, нормировать сферические функции можно и не только под тем
условием, которое было поставлено выше — связь между обычными сфериче-
скими функциями и нормированными можно установить, например, при помощи
соотношений
^(е) = г
пк
Р(е), где г
пк
= д
пк
/2ге+1;.
Р
п
(соз 0) =
1/2П
+
1
р
п
(соз 0).
При таком нормировании среднее квадратическое значение сферической
функции по всей поверхности сферы будет равно единице, т. е.
со
— так называемые полностью нормированные функции.
Если функцию / (0, А) разложить в ряд полностью нормированных сфери-
ческих функций
со п
/(0, Я) = 2 2 (А
пк
С08кХ + В
пк
5ткХ)Р
пк
(д),
п=0 й=0
Таблица 2
дп
к
=
-1/2 (п — А)1
V [п+т '
Яп
°-
= 1; г
пк
= д
пк
У 2п + 1
п к
ЧпЬ
/2п + 1
г
пк
0
1
2
3
4
0
0
1
0
1
2
0
1
2
3
0
1
2
3
4
1,00000000
1,00000000
1,00000000
1,00000000
0,57735027
0,28867513
1,00000000
0,40824829
0,12909944
0,52704628 X 10"
1
1,00000000
0,31622777
0,74535599 X 10"
1
0,19920477 X 10"
1
0,70429521 X 10"
2
1,00000000
1,73205081
2,23606798
2,64575131
3,00000000
1,00000000
1,73205081
1,73205081
2,23606798
0,12909945 X 10
0,64549721
2,64575131
0,10801234 X 10
0,34156501
0,13944334
3,00000000
0,94868331
0,22360680
0,59761431 X 10"
1
• 0,21128856 X 10"
1
6 Заказ 1379
81

то коэффициенты разложения определятся по формулам
А
пк
= 4г 11 /
(
0
'> ~
р
пк
(9") соз кХ' йщ
т
в
пк
= 0 / (0', (0") 31П ЛЯ' Ло.
(о
Связь между коэффициентами различных разложений для названных
«случаев устанавливают при помощи соотношений
~д Л-пк _ =? А
пк
_
пк — „ . ,
1пк '
ПК
г
пк
'
ТГ В
пк
ВПЙ
1пк ' "" г
пк
'
где одна черта над буквой соответствует нормированным, а две черты — пол-
ностью нормированным коэффициентам.
Приводятся значения коэффициентов д
пк
и г
пк
до четвертой степени
(табл. 2).
§ 18. МЕТОДЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ
РАЗЛОЖЕНИЯ ФУНКЦИИ, ЗАДАННОЙ НА СФЕРЕ,
В РЯД ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ
При решении теоретических вопросов, связанных с определением фигуры
Земли, различные величины, полученные из измерений в отдельных точках
земной поверхности, приходится обобщать на всю земную поверхность, пред-
ставляя их в качестве функций сферических координат, используя для этого
разложения в бесконечные ряды по сферическим функциям. На практике,
разумеется, всегда ограничивают разложение до определенной степени т,
пренебрегая всеми последующими членами разложения. Вопрос об определе-
нии степени, какой следует ограничить разложение функции, решается в зави-
симости от имеющегося материала наблюдений и от точности, с которой тре-
буется представить искомую функцию. Отдельные разложения выполнялись
до 4, 8, 16 и даже до 40-й степени.
Если разложение в ряд по сферическим функциям производится до сте-
пени т, то число коэффициентов разложения, подлежащих определению, будет
(т + I)
2
. Задача определения этих коэффициентов при разложении до высоких
степеней является в техническом отношении весьма сложной.
Существующие методы определения коэффициентов разложения можно
разбить на две группы. К первой группе относят методы, основанные на опре-
делении коэффициентов разложения по имеющимся значениям функции
в отдельных точках сферы; ко второй — по осредненным значениям функции
,на некоторых площадях, покрывающих сферу.
Для первой группы функция может быть представлена в обычном виде
т п
/ (9, Я) = 2 2 (Апк соз
ЛЯ
+ В
пк
зт кХ) Р
пк
(6), (111.31)
Л-О
к=0
где / (6, Я) — известное значение.функции в точке сферы с координатами 0 и Я.
.32

В этом случае задача определения коэффициентов А
пк
и В
пк
может быть
значительно упрощена, если значения функции будут даны не в произвольных,
а в определенным образом выбранных точках. В зависимости от принимаемой
системы расположения точек используют различные способы определения
коэффициентов: способ Гаусса и два способа Неймана.
Для второй группы разлагаемая в ряд функция представляется
т п
/1Р = 22 [(А
пк
соз кХР
пк
(0) + В
пк
81 п кХР
пк
(0)], (111.32)
п=О Ь=0
где черт ой отмечены величины, осредненные по некоторым площадям сферы.
При определении тем или иным методом коэффициентов различных раз-
ложений приходится учитывать один существенный факт, в значительной сте-
пени усложняющий весь процесс вычисления коэффициентов.
Так как значения функции / (0, Я) в отдельных точках определяются из
наблюдений, а наблюдения в большинстве случаев очень неравномерно распре-
делены по земной поверхности, это приводит к существенному искажению
результатов вычислений.
Поэтому для ослабления влияния неравномерности распределения точек,
в которых определена функция / (0, Я), при определении коэффициентов раз-
ложения выгоднее использовать методы, которые предусматривают использо-
вание осредненных результатов. Рассмотрим некоторые методы.
1. Способ Гаусса
Пусть требуется выполнить разложение функции / (0, Я) в рядно сфери-
ческим функциям до степени т.
На (т + 1) произвольно выбранных параллелях в точках, равноотстоящих
друг от друга по долготе, задаются значения / (0, Я) таким образом, что на одной
параллели дается одно значение, на второй — три, на третьей — пять и т. д.
и на (т + 1) параллели — (2т + 1) значение. Всего, таким образом, задается
(т + I)
2
значений функции / (0, Я), что равно числу определяемых коэффи-
циентов А
пк
и В
пк
.
Тогда совокупность значений / (0, Я) на любой параллели (т. е. при 0 =
= сопз1) может быть представлена рядом Фурье по синусам и косинусам дол-
готы Я. Обозначая коэффициенты этого ряда через р
к
и д
к
, для п-й параллели
напишем
/ (Я) = р
0
+ р
х
сов
Я
+ р
г
сов
2Я
+ . .
.
+ р„ соз пХ + зт
Я
+
+ д
2
зт 2Я + ...-{- д
п
зт пХ. (III.33)
Для определения коэффициентов р
к
и этого ряда воспользуемся свой-
ством ортогональности функций, по которым производится разложение в ряд
Фурье.
Как известно, две вещественные функции § (х) и к (х), заданные на конеч-
ном интервале а < х <[ Ъ, ортогональны на этом интервале, если
ь
Ц
$ (х) к (х)
с1х —
0.
а
Понятие ортогональности при этом во многом аналогично условию пер-
пендикулярности двух векторов, заданных своими декартовыми проекциями.
Система функций называется ортогональной на некотором интервале, если
115"

каждые две функции из этой системы ортогональны друг другу на этом интер-
вале. Исторически первым и наиболее важным примером ортогональной си-
стемы функций явилась система функций
1, соз х, зтж, соз2;г, зт2х, . . . соз гая, зтгая,
на интервале —я ^ х ^ я. Легко убедиться в том, что она действительно
ортогональна:
я
соз пх соз тх йх =
О,
-я
я
31П
пх зш тх йх =
О,
-я
я
соз пх
зхп
тх йх = 0.
-я
Если произвольная функция / (х) на интервале а < х <; Ь разложена
в ряд по ортогональным на этом интервале функциям (х)
00
/ (х) = <я) +
а-1%2
{х) + . . . + а
п
8
п
(х) + . . . = 2
а
пёп (х),
п=0
-то для определения коэффициентов этого ряда умножим обе его части на §
п
(х)
и, проинтегрировав по интервалу а х ^ Ъ, получим
ь ь ь
§
1
(х) ё
п
(х) йх = а
г
| (х)
%
п
(х)
Лх
+ а
2
^ (х) (х) йх +
а а а
Ь
+ .
•
. + а
п
^ё%{х)йх+. . .
а
В силу ортогональности системы функций ^ (х) в правой части равенства
все интегралы равны нулю, за исключением интеграла от (х), поэтому най-
дем, что
ь
5
/ (я) ёп (*)
ах
а
п
= —
ь
.
(ге
= 1, 2, 3, . . .)
а
Применив полученную формулу для вычисления коэффициентов ряда
Фурье, получим
я
/ {X)
ах л
ро=^—
| ах -я
-я
;84

я
| /
(X)
соз
кХ д,Х
я
]' соз^кХаХ -Я
я
|
/ (X) Вт кХ йХ
я
& = ^ = Т и
{Х)
з1п кК
81П2
кХЛХ
-Я
-я
Если подынтегральная функция на данной параллели задана в п отдельных
равноотстоящих по долготе точках, то коэффициенты р
0
, р
к
и д
к
определяются
по формулам
1=1
га
Рк
= — ^Н
1
д созкХ„
1=1
п
АХ
1=1
или при
п п
М=
"1Г' Рк=—^НК)
С05к
Ч
Як
=
1=1 1=1
п
1 = 1
Таким образом, мы рассчитаем число значений для:
Р
0
т+ 1,
и ?! т,
Рг и тп 1,
Рз
и
Чз тп — 2,
Рт К
Ят
1,
«1 всего (т + I)
2
значений.
Тригонометрические многочлены (111.31) и (III.33) в выбранных точках
: заданными значениями функции / (9, Я) должны совпадать, так как соот-
ветствуют одним и тем же значениям функции / (0, Я).
Следовательно, для точек (т + 1)-й параллели напишем
/ (0, Я) = А
00
+ А
1о
Р
г
(СОЗ 9) + {А
п
соз Я + В
п
зт Я) Р
п
(0) + А,
0
Р
г
(соз 0) +
+ (А
21
СОЗ
Я
+ В
а
зт
Я)
Р
21
(9) + (Л
22
соз
2Я
+ Я
22
зт 2Я) Р
22
(9) +
85

+ А
30
Р
3
(соз 0) + . . . + (А
33
созЗА+ В
33
дщ ЗА) Р
33
(0) + . . . +
+ А
т0
Р
т
(соз 0) + . .
•
+ (А
тт
соз
то
А + В
тт
зт тоА) Р
тт
(0) = р
0
+ р
г
соз А +
+Рг соз
2А
+
Рз
соз ЗА +. .
.
+ р
т
соз
тоА
-ф- д
х
зт
А
+
Яг
зт 2А
<?
3
зт
ЗА
+ . .
.
+
+ д
т
зттоА.
Сравнивая коэффициенты при соответствующих синусах и косинусах
кратных дуг двух многочленов, устанавливаем, что коэффициент р
0
должен,
соответствовать совокупности тех членов разложения (111.31), которые не
содержат долготы, т. е.
р
0
= А
00
+ А
и
Р
х
(соз 0) + А
20
Р
2
(соз 0) + . . . + А
т
Р
т
(соз 0).
Таких уравнений будет (то + 1), что соответствует числу найденных зна-
чений р
0
. Они образуют систему с (то + 1) неизвестными А
00
, А
10
, А
20
, . . .,
А
т0
, в которой коэффициентами будут значения полиномов Лежандра Р
г
(соз 0),
Р
2
(соз 0), . . ., Р
т
(соз 0) для 0, соответствующих данным (п + 1) паралле-
лям. Из решения этой системы определятся все неизвестные коэффициенты
А
оо> •
•
•»
А
тд
.
Далее, выбирая из ряда (111.31) члены, которые имеют множителем соз А,
и приравнивая их сумму коэффициенту р
х
, получим уравнение
Рг
=
А
ХХ
Р
ХХ
(0) + А
21
Р 21 т1 (9)
и аналогично для членов, содержащих зт А
Ях
= В
ХХ
Р
Х1
(0) + В
21
Р
2Х
(0) +. . . +В
т1
р
т1
(0).
Таких уравнений в каждой группе будет то (что соответствует числу коэф-
фициентов р
х
и д
х
). Таким образом, для определения коэффициентов А
п
,
. . ., А
т1
, В
1Х
, . . ., В
тх
необходимо решить две системы уравнений с то неиз-
вестными в каждой. Аналогично получим
Рг ~ А
22
Р22
(0) + . . . + А
т2
Р
т2
(0) 1 ^
п я р л. 4-к р ( (
п
уравнение,
Яг = В
22
Р
22
(И) +. . . + В
т2
г
т2
(0) )
Рз = А
33
Р
33
(0) +. . . + А
тз
Р
тз
(0) |
п Р
т\
л. л.яр /м " — 2 Уравнения,
Яз = зз зз (0) +
•
•
•
+ В
та
Р
тз
(0) I
Рт —
А
тт
Р
тт
(0) )
„ р «и Г
одно
УР
авнение
-
Ут — -°тт
г
тт\Р) )
Так, постепенно найдем все коэффициенты А
пк
и В
пк
, причем не решая
систем больше, чем с (то + 1) неизвестным.
Можно, однако, не ограничиваться ни числом параллелей, ни числом задан-
ных на них значений функций. В этом случае задачу решают по способу наи-
меньших квадратов.
Применение способа Гаусса, а также его дальнейшее использование для
вычисления значений / (0, А) по формуле (111.31) для любой точки сферы и срав-
86

нение результатов вычисления с наблюденными значениями / (0, А) требует
вычисления полиномов Лежандра и присоединенных функций Р
пк
(0). Обычно
эти вычисления на практике выполняют с помощью ЭВМ.
2. Способ Неймана
Способ Неймана, как и способ Гаусса, основан на использовании значений
разлагаемой в ряд функции / (0, А), заданных в точках пересечения параллелей
и расположенных через равные интервалы друг от друга меридианов. Сначала
для каждой параллели выполняют разложение функции в ряд Фурье, ограни-
чиваясь членами заданной степени т. Коэффициенты ряда Фурье определяют
по формулам Бесселя.
Для определения коэффициентов разложения функции / (9, А) по сфери-
ческим функциям Нейман предложил два метода численного интегрирования.
В первом методе требуется задать значения / (0, А), выбранные на пересече-
нии 2т равноотстоящих меридианов с 2т + 1 произвольными параллелями.
Во втором методе значения функции / (0, А) задают на пересечении 2т равно-
отстоящих меридианов ст + 1 параллелями, но здесь в отличие от первого
метода параллели для каждого т строго определены.
3. Вычисление по способу наименьших квадратов
При этом методе вычисления коэффициентов ряды (111.31) рассматриваются
в качестве уравнений погрешностей и коэффициенты А
пк
и В
пк
находятся
под условием
2
/(0, А)-2 где, А)
= Ш1П.
Если значения функции / (0, А) даны не в отдельных точках, а осреднены
по некоторым площадям, то в этом случае уравнения погрешностей соста-
вляются в виде (111.32).
4. Метод численного интегрирования
Поверхность единичной сферы, по которой совершается интегрирование,
разбивается на достаточно большое число элементарных площадок Доз. Если
для каждой площадки А
со
известно осредненное значение функции / (0, А),
то заменяя в (III.30) интегралы суммами, получаем формулы для вычисления
коэффициентов
а
ю
=
1
2 ^га
р
« <
со3 е
')
Асо;
А
пк
= 2ПвП
7
) ^Д9')со8/СА'АСО;
В
<*=-^Г- 2
/(9
"' Дю;
чертой отмечены осредненные по площади А со величины.
87
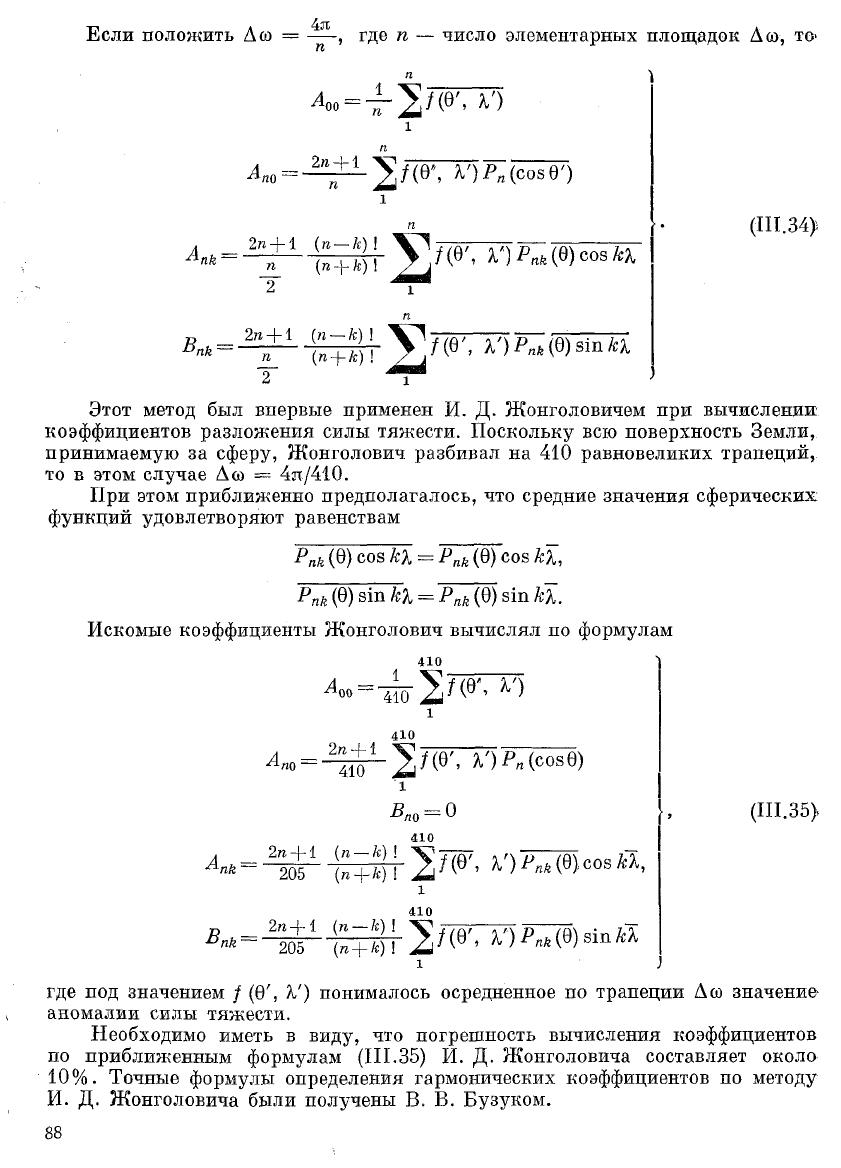
Если положить
А (о
= где п — число элементарных площадок
Д со,
то>
Ло=4-2
/(0
''
}/)
1
2га + 1
2/(6", Я')Р„(С08б')
1
2д +
1
(п — к)
!
п_ (га + /е)!
2 1
/(6', Г)Р„
Й
(0)СО8^
(111.34)
п
еует;
~2~ 1™
Этот метод был впервые применен И. Д. Жонголовичем при вычислении
коэффициентов разложения силы тяжести. Поскольку всю поверхность Земли,
принимаемую за сферу, Жонголович разбивал на 410 равновеликих трапеций,
то в этом случае Дсо = 4я/410.
При этом приближенно предполагалось, что средние значения сферических:
функций удовлетворяют равенствам
Р
пк
(6) соз
к%
= Р
пк
(9) соз кк,
Р
пк
(9) вт кк = Р
пк
(9) зт кк.
Искомые коэффициенты Жонголович вычислял по формулам
410
_
2в
+
1_
- 4Ю
410
2/(0'. Я')^(СО8 0)
Вп 0 = 0
1-пк -
2ге
+ 1
(га
—/с)!
410
В
п
к =
205 (ге+/с)!
2ге +
1 (га —к)
!
205 (п-\-к) !
2/Г. Я')
Р
П
к (6).
соз кк,
1
410
2/(9'. Г) Р
пк
{Щ зшАА,
(111.35).
где под значением / (0', к') понималось осредненное по трапеции Дсо значение-
аномалии силы тяжести.
Необходимо иметь в виду, что погрешность вычисления коэффициентов
по приближенным формулам (III.35) И. Д. Жонголовича составляет около
10%. Точные формулы определения гармонических коэффициентов по методу
И. Д. Жонголовича были получены В. В. Бузуком.

Средние интегральные значения сферических функций для соответству-
ющих стандартных трапеций А©, ограниченных параллелями 0
Х
и 0
2
и мери-
дианами А] и А
2
, следует вычислять по формулам
Ь ^ Г соз
кХ)
Л
7 ГТТ I Рпй(0)зт0й0
ГсозШ
е
>>
у
/ (зт м)
Р„(СО8 0):
Дсо
02 Я.2
| Р
п
(СОЗ
0) 81П0Й0 ]' аХ
вг %1
Доз
Выполнив в (111.36) интегрирование по К и обозначив
е
2
Ф
Л
*(е) = ]Р„
й
(0)8П10й0,
В. В. Бузук получил
е:
(111.36)
Р
(е
Л
С08А:Я
)_ ФпП9)
/8Ш&Я.
а
—вш&А*
пк
^
'{зт/сА) \соз кХ
х
— соз к%
2
рдсоз0)=
Таким образом, точные формулы для вычисления коэффициентов А
пк
и В
пк
принимают вид
Пк\
_ (2га
—{—
1) (га—
к)'\
\В
пк
) 2 кл(п + к)\
2га+ 1
•Д, ГЗШ&Ао— 8Щ&А1
2/(0', Я')Ф
яА
(в){
со8к%1
_
С08кх
4л
2/(0'' ЛФ
ло
(0)а
2
-и
§ 19. ИСПОЛЬЗОВАНИЕ СФЕРИЧЕСКИХ ФУНКЦИЙ
ДЛЯ РЕШЕНИЯ НЕКОТОРЫХ КРАЕВЫХ ЗАДАЧ
ДЛЯ СФЕРЫ
При определении внешнего потенциала планет предварительно оказы-
вается выгодным представить потенциал в виде ряда сферических функций.
В таком случае решение краевых задач может быть выполнено при помощи
сферических функций.
Выясним на частных примерах методику подобных решений.
Внутренняя и внешняя задачи Дирихле для сферы решаются следующим
образом. Пусть на сфере радиуса В задана функция / (0, Я). Ее всегда можно
представить в виде бесконечного ряда сферических функций (111.25). Входящие
в этот ряд сферические функции У
п
(д, Я) определяются по формулам (111.29)
и (III.30). После того как У
п
(0, Я) найдены, их следует подставить в ряды
(111.22) и (111.24), которые определяют гармонические функции внутри и вне
сферы, т. е. решают внутреннюю и внешнюю задачи Дирихле.
89
