Шпаргалки - Логика

Подождите немного. Документ загружается.

1. Мышление как объект формальной

логики.

Мышление человека подчиняется логическим

законам и протекает в логических формах

независимо от науки логики. Люди мыслят

логично, не зная её правил, подобно тому, как они

правильно говорят, не зная правил грамматики.

Мышление - это сложный, многосторонний

процесс, высшая форма познания мира,

свойственная только человеку. Человеку присущи

различные типы мышления: теоретическое, а

также практическое.

Основное различие между теоретическим и

практическим видами мышления состоит в том,

что они по разному связаны практикой. Так

практическое мышление в основном направлено

на разрешение частных конкретных задач

жизнедеятельности людей, тогда как

теоретическое мышление направленно в основном

на нахождение общих закономерностей

познаваемой действительности.

Логика изучает основной тип мышления –

понятийное (абстрактное) мышление.

Абстрактное мышление – это процесс

рационального отражения материального мира в

понятиях, суждениях, умозаключениях, гипотезах,

теориях, позволяющих проникать в сущность и

закономерные связи предметов и явлений,

творчески преобразовывать их сначала в теории, а

затем на практике.

Форма мышления – способ связи элементов

мысли, ее строение, благодаря чему содержание

существует и отражает действительность. Т.е.

различные предметы отражаются в абстрактном

мышлении одинаково - как определенная связь их

существенных признаков, т.е. в форме понятия.

Понятие - форма мышления, в которой

отражаются существенные признаки

одноэлементного класса. Понятия в языке

выражаются словами (например, "дерево",

"самолет") или группой слов, т.е.

словосочетаниями, например, "студент

гуманитарного института", "создатель

художественных картин", "река Дон",

"космический корабль" и др.

Суждение — это высказывание,

устанавливающее связь между двумя понятиями.

Например, «Железо есть элемент», «Змеи не

имеют ног». Та часть суждения которая

отображает предмет мысли, называется субъектом

суждения и обозначается буквой S, а та часть

суждения, которая отображает то, что

утверждается (и отрицается) о предмете мысли,

называется предикатом суждения и обозначается

буквой Р. Слово есть (или суть - когда много

предметов) называется связкой. Суждение можно

изобразить символически в виде формы:

S есть (не есть) P, где S и P – переменные,

вместо которых можно подставить какие-то

определенные мысли о предметах и их свойств, а

Изменение свойств предметов и отношений

между ними отражается в форме умозаключений.

Умозаключение - это такая форма мышления,

посредством которой из одного или нескольких

суждений, называемых посылками, по

определенным правилам получается заключение.

Виды умозаключений и изучает логика. Приведем

пример:

Все металлы - вещества

Железо - металл

Железо - вещество

Первые два суждения, которые находятся над

чертой, называются посылками, а третье суждение

называется заключением. Черта под исходными

суждениями заменяет слова «следовательно»,

«значит». Но не всякое сочетание суждений

является умозаключением. Между суждениями

должна быть логическая связь, в которой

отображается взаимозависимость предметов и

явлений объективного мира. Следовательно,

каждая из основных форм абстрактного мышления

имеет нечто общее, что не зависит от конкретного

содержания мысли, т.е. свою специфическую

структуру.

Форма абстрактного мышления -это способ

связи элементов мысли, ее строение, благодаря

которому содержание существует и отражает

действительность.

2. Предмет формальной логики и понятие

логического закона

Формальная логика – это наука о формах

мышления, о формально-логических законах и

других связях и отношениях между мыслями

по их логическим формам. Исследуя

необходимые связи между мыслями по

логическим формам – логические законы,

логика формулирует утверждения об

истинности всех высказываний определенной

логической формы. Эти утверждения тоже

называются законами, но в отличии от

логических законов (связей, существующих

независимо от того, знаем мы о них или нет) –

законами (науки) логики. Законы логики,

после того как они сформулированы,

выступают в качестве норм, в соответствии с

которыми должны осуществляться

рассуждения. В логике разрабатываются также

требования другого рода, которые

рекомендуются выполнять в процессе

познания.

Формальная логика, таким образом, является

нормативной наукой о формах, законах и

приемах интеллектуальной познавательной

деятельности.

Логический закон – это логическая форма,

которая гарантирует истинность высказывания

при любом содержании. В данном

определении выдвигаются две основные

стороны высказывания: содержательная и

формальная.

С изменением содержания высказывания

меняется и содержательная связь, а

формальная может повторяться сколь угодно

долго. На основе этого положения и выводится

понятие логического закона. Формальная связь

между мыслями называется также логической

связью. Это связи между признаками в

понятии и самим понятием, между элементами

суждения и самим суждением.

Законы логики имеют определенную

задачу. Она заключается в формулировке

основания, фундаменте правил и

рекомендаций, следуя которым можно достичь

истины. Поэтому логические законы не

являются законами в собственном смысле

этого слова, так как этот термин используется

для описания явлений и предметов

действительности. Логические законы

отражают реальные, объективные связи между

высказываниями: объединение, разъединение,

обусловленность и пр.

3. Возникновение логики как науки.

Основные этапы развития логики.

Формальная логика в своем развитии прошла

два основных этапа.

Первый этап - это связь с работами Аристотеля,

в которых дано систематическое изложение

логики. Основным содержанием логики

Аристотеля является теория дедукции, также

содержаться элементы математической логики.

Аристотель сформулировал основные законы

мышления: тождества, противоречия и

исключенного третьего, описал важнейшие

логические операции, разработал теорию понятия

и суждения, обстоятельно исследовал дедуктивное

умозаключение.

Учение о силлогизме составило основу одного

из направлений современной математической

логики - логике предикатов. Дополнением к этому

учению была логика античных стоиков (Зенон,

Хрисипп и других). Логика стоиков -основа

другого направления математической логики -

логики высказываний.

Следующими, кто развил учение Аристотеля,

следует назвать Галена; Порфирия, который

разработал схему отображающую отношения

между понятиями; Боэция, сочинения которого

были логическими пособиями.

Логика развивалась и в средние века, однако

схоластика исказила учение Аристотеля,

приспособив его для обоснования религиозной

догматики. Значительны успехи логической науки

в Новое время. Важнейшим этапом в ее развитии

явилась теория индукции, разработанная Ф.

Беконом. Он подверг критике дедуктивную

логику, которая не может служить методом

научных открытий. Методом должна быть

индукция. Разработка индуктивного метода -

огромная заслуга Бекона. Методы дедукции и

индукции не исключают друг друга, а дополняют.

Дж.С.Милль систематизировал методы научной

индукции. Дедуктивная логика Аристотеля и

индуктивная логика Бекона Милля составили

основу общеобразовательной дисциплины и

составляют основу логического образования в

настоящее время.

Второй этап – это появление математической

логики. Философ Г. В. Лейбниц считается

основоположником. Он пытался построить

универсальный язык, с помощью которого споры

между людьми можно было разрешить

посредством вычисления. Математическая логика

изучает логические связи и отношения, лежащие в

основе дедуктивного вывода. Для выявления

структуры вывода строят различные

математические исчисления.

4. ЛОГИКА И ЯЗЫК ПРАВА

Логика- наука о мышление, где мышление

рассматривается как средство познания (не в

физиологическом, психологическом или каком-

либо другом смысле).

Мышление- это процесс активного

опосредованного отражения действительности в

обобщённых образах, неразрывно связанный с

языком

Никто не будет спорить, что навыки

правильного мышления помогают человеку

улучшить свою жизнь.

Предметом логики яв. законы и формы, приёмы и

операции мышления, с помощью кот. чел. познаёт

окруж. мир.

В жизни не сущ. формы без содерж., но нам

часто не интерестно содержание, т.к. важно

изучить общие приёмы и способы лог. мышления

и уже потом применять их к конкрет. содержанию.

Многие люди мыслят правильно, но изучать

логику в ВУЗе просто неободимо, т.к. это

повышает навыки этого самого правильного,

логичного мышления, логика позволяет нам

исправить потенциальные ошибки в рассуждениях

Задача логики- научить человека сознательно

применать законы и формымышления, на основе

этого логичнее мыслить, правильно познавать мир.

Логикка повышает культуру мышления,

вырабатывает новые навыки.

Знание логических законов, умение применять

их на деле, навыки последовательных

рассуждений и аргументации для юриста-

необходимые для успешной раброты качества.

Примером может послужить Шерлок Холс с его

дидуктивным методом, многочисленная плеяда

русских юристов, блещющих пламенными,

хорошо аргументироваными речами, но это и

рядовые труженники прокуратуры, организующие

свои следственные будни в соответствие и с лог.

зак., их способность построить следственную

версию, раскрыть уловки приступника. Не надо

забывать, что деятельность юристов связанна не

редко с судьбами людей, их жизнями, и

логическая ошибка может дорого стоить. В этой

профессие требуется особая точность мышления.

Особая область отношений, регулируемых

правом, (правоотношения) обусловливает

специфику языка права. Эта специфика

заключается в употреблении терминов, которые

должны пониматься единообразно разными

людьми в различных случаях и ситуациях. Такие

термины называются юридическими. Например, в

обыденной жизни мы можем употреблять

выражения “Сегодня ночью был дождь”,

“Сегодня ночью на улице был сильный шум”,

“Петров — коренной москвич”, “Иванов является

участником Великой Отечественной войны”.

Входящие в эти выражения слова и

словосочетания “ночь”(“ночное время”),

“коренной москвич”, “участник ВОВ” разными

людьми понимаются по-разному. Так, время 22

часа 50 минут одни отнесут к ночному времени, а

другие к вечернему, одни считают коренным

москвичом человека, родившегося в Москве, другие

— человека, у которого к тому же и родители

родились в Москве, третьи — того, кто много

лет живёт в Москве, одни считают участниками

ВОВ только тех, кто непосредственно

участвовал в боевых действиях, а другие — ещё и

тех, кто находился на фронте, но

непосредственно не участвовал в боевых

действиях (к примеру, хирургов, работавших в

полевых госпиталях). Такая неопределённость

выражений обыденного языка оказывается

неприемлемой при решении правовых вопросов.

Допустим, что имеется закон, запрещающий

ночные полёты самолётов над крупными

населёнными пунктами. Самолёт пролетает над

городом в 22 часа 50 минут. Нарушен закон или

нет? Другая ситуация. Несколько лет назад было

принято постановление о постановке на очередь

коренных москвичей, проживающих в

коммунальных квартирах, для получения ими

отдельных квартир. Кто имеет право на

постановку на очередь? Третий случай. В Думе

решается вопрос о льготах участникам ВОВ. Для

этой цели выделяется особая статья в бюджете.

Как подсчитать расходы на эти цели, не

уточнив, кого следует считать участником ВОВ?

Чтобы избежать неопределённостей, взамен

выделенных выше выражений обыденного языка,

вводят юридические термины посредством

следующих определений: “Ночное время — это

время с 10 часов вечера до 6 часов утра”,

“Коренной москвич — это человек, который

прожил в Москве 40 лет”, “Участник BOB — это

человек, который служил в действующей армии”.

Есть и другие способы введения юридических

терминов: введение в качестве юридических

терминов выражений, которых нет в обыденном

языке; разъяснение выражений посредством

примеров, описаний, характеристик и т.д.

Кроме юридических терминов в языке права

используются и не уточняемые в нем выражения.

Это выражения, которым придан точный смысл в

других науках, а также те, которые не являются

многосмысленными в обыденном языке. Так,

определяя коренного москвича как человека,

который прожил в Москве 40 лет, мы однозначно

понимаем выражения “жить в Москве”, “40 лет”,

“человек”. Эти выражения не нуждаются в

уточнении.

5. Понятие как центральная категория

логики. Приемы образования и логическая

структура понятия.

Способность познавать внешний мир

посредствам идей, отражающих предметы в их

общих и существенных признаках, создает

общезначимую логическую форму мышления –

понятие. Без понятия нельзя сформулировать

законы и выделить предметную сферу науки.

Понятие помогает выделить определенные классы

вещей и отличить их друг от друга. Любые

свойства, черты, состояние предмета, которые, так

или иначе, характеризуют предмет, выделяют его,

помогают распознать среди других предметов,

составляют его признаки.

Признаком предмета называется то, в чем

предметы сходны друг с другом или чем они друг

от друга отличаются. Признаками могут быть

не только свойства, принадлежащие предмету;

отсутствующее свойство (черта, состояние)

также рассматривается как его признак. Любой

предмет имеет множество разнообразных

признаков. Одни из них характеризуют

отдельный предмет и являются единичными,

другие принадлежат определенной группе

предметов и являются общими. Так, каждый

человек имеет признаки, одни из которых,

например, черты лица, телосложение, походка,

мимика, так называемые особые приметы,

броские признаки, принадлежат только данному

других людей. Другие профессия,

национальность, социальная принадлежность и

т. д. являются общими для определенной группы

людей. И, наконец, есть признаки, общие для всех

людей. Они присущи каждому человеку и вместе с

тем отличают его от всех других живых

существ. К ним относятся способность

создавать орудия труда, способность к

абстрактному мышлению и членораздельной речи.

Кроме единичных (индивидуальных) и общих

признаков логика выделяет признаки

существенные и несущественные. Признаки,

необходимо принадлежащие предмету,

выражающие его сущность, называют

существенными. Они могут быть общими и

единичными. Понятия, отражающие множество

предметов, включают общие существенные

признаки (напр. способность создавать орудие

труда). Понятие, отражающее один предмет

(напр. “Аристотель”), наряду с общими

существенными признаками (человек,

древнегреческий философ) включает единичные

признаки. Признаки, которые могут

принадлежать, но могут и не принадлежать

предмету и которые не выражают его сущность,

называются несущественными.

Понятие – одна из основных форм научного

познания. Формируя понятие, наука отражает в

них изучаемые ею предметы, явления, процессы.

Логические приёмы образования понятий.

Что бы составить понятие о предмете, нужно

сравнить данный предмет с другими предметами,

найти признаки сходства и различия. Логический

прием, устанавливающий сходство или различие

предметов, называется сравнением. Выделение

признаков связано с мыленным расчленением

предмета на составляющие его части, стороны,

элементы. Мысленное расчленение предмета на

части называется анализом. Выделение с помощью

анализа признаков позволяет отличить

существенные признаки от несущественных. Это

мысленное выделение признаков, называется

абстрагированием. Элементы, стороны, признаки

предмета, выделенные с помощью анализа,

должны быть соединены в единое целое. Это

достигается с помощью приёма,

противоположного анализу, - синтеза,

представляющего собой мысленное соединение

частей предмета, расчлененного анализом.

Признаки изучаемых предметов

распространяются на все сходные предметы. Эта

операция осуществляется путем обобщения, с

помощью которого определенные предметы на

основе присущих им одинаковых свойств

объединяются в группы однородных предметов.

Понятие, как логическая форма мышления, имеет

свою структуру, которая включает два основных

элемента: содержание и объем.

Содержание понятия - это совокупность

существенных признаков предмета, мыслимого в

понятии. Так, содержанием понятия "человек"

является общественное существо, способное

производить орудия труда. А содержанием

понятия "государство" выступает власть

экономически господствующих социальных сил и

т.д.

Объемом понятия называется совокупность

(класс) предметов, которая мыслится в данном

понятии. Например, объем понятий "растение",

"животное", "товар" выражает всю безграничную

совокупность соответствующих предметов

реальной действительности.

6. Виды понятий по объему.

Как цельная форма мысли понятие

представляет собой закономерное единство двух

составляющих его элементов: объема и

содержания. Содержание и объем понятия тесно

взаимосвязаны. Эта взаимосвязь выражается в

законе обратного отношения между объемом и

содержанием понятия, который устанавливает, что

увеличение содержания понятия ведет

уменьшению его объема, и наоборот.

Объем — структурный элемент понятия,

отражающий собой совокупность предметов,

обладающих одинаковыми существенными и

отличительными признаками. Так, объем понятия

«стол» отражает собой всю совокупность столов

на нашей планете, все их множество, весь их

класс. Объем понятия «человек» -

пятимиллиардное население планеты. В

зависимости от содержания и объема все понятия

делятся на конкретные виды.

По объему понятия бывают: единичные,

общие, нулевые. Единичными называются

понятия, в которых мыслится один предмет

(например, "великий русский писатель Александр

Николаевич Островский", "Организация

Объединенных Наций", "столица России" и

другие). Общим называется понятие, в котором

мыслится множество предметов (например,

"столица", "государство", "правовед", "экономист"

и другие).

Общие понятия могут быть

регистрирующими и нерегистрирующими.

Регистрирующими называются понятия, в

которых множество мыслимых в них предметов

подается учету, регистрации (например, "участник

Великой Отечественной войны", "народный

депутат России" и другие). Нерегистрирующим

называется общее понятие, относящееся к

неопределенному числу предметов (например,

"человек", "философ", "ученый" и другие).

Нерегистрирующие понятия имеют бесконечный

объем.

Нулевыми (пустыми) называются понятия,

объемы которых представляют собой классы

реально не существующих предметов и

существование которых в принципе невозможно:

"вечный двигатель", "русалка", "леший" и др.). От

нулевых следует отличать понятия, отражающие

предметы, которые реально не существуют в

настоящее время, но существовали в прошлом или

существование которых возможно в будущем:

"древнегреческий философ", "термоядерная

электростанция". Такие понятия не являются

нулевыми.

7. Виды понятий по содержанию

Как цельная форма мысли понятие

представляет собой закономерное единство двух

составляющих его элементов: объема и

содержания. Содержание и объем понятия тесно

взаимосвязаны. Эта взаимосвязь выражается в

законе обратного отношения между объемом и

содержанием понятия, который устанавливает, что

увеличение содержания понятия ведет

уменьшению его объема, и наоборот.

Виды понятий по содержанию: конкретные и

абстрактные, абсолютные и относительные,

положительные и отрицательные, собирательными

и несобирательными.

Конкретные - это понятия, в которых мыслится

предмет или совокупность предметов как нечто

самостоятельно существующее: "академия",

"студент", "романс", "дом", "поэма А. Блока

"Двенадцать" и др.

Абстрактные - это понятия, в которых

мыслится не сам предмет, а какой-либо из

признаков предмета, взятый отдельно от самого

предмета: "смелость", "добросовестность",

"храбрость", "синева", "тождество" и др.

Относительные

- это такие понятия, в которых

мыслятся предметы, существование одного из

которых предполагает существование другого: "

родители "-" дети "," учитель "- "ученик ","

начальник "-" подчиненный "," истец "-" ответчик

" и др.

Безотносительные - это такие понятия, в

которых мыслятся предметы, существующие

самостоятельно, вне зависимости от другого

предмета: "фермер", "правило", "деревня",

"человек" и др.

Положительные - это понятия, содержание

которых составляют свойства, присущие

предмету: "принципиальность", "благородный

поступок", "живущий по средствам", "успевающий

студент" и др.

Отрицательными называются понятия, в

содержании которых указывается на отсутствие у

предмета определенных свойств (например,

"некрасивый поступок", "некрашеный дом",

"некошеный луг" и др.).

В русском языке отрицательные понятия

выражаются обычно словами с отрицательными

приставками "не" или "без" ("бес "):

"неграмотный", "неверующий", "беззаконие",

"беспорядок" и др. В словах иностранного

происхождения - чаще всего словами с

отрицательной приставкой "а": "агностицизм",

"аморальный" и др.

Собирательными называются понятия, в

которых группа однородных предметов мыслится

как единое целое: "лес", "созвездие",

Собирательные понятия бывают общими (роща,

хор) и единичными «созвездие Большая

Медведица». Содержание собирательного понятия

нельзя отнести к каждому отдельному элементу,

Несобирательные - это такие понятия,

содержание которых можно отнести к каждому

предмету данного класса, который охватывается

понятием: "дерево", "звезда", "студент" и др.

Определить, к какому из указанных видов

относится конкретное понятие, означает дать

ему логическую характеристику. Например,

«РАКЕТА» по объему является общим (в нем

мыслиться более одного предмета: ракета

космическая, боевая), нерегистрирующим

(относится к неопределенному числу предметов

т.к. мы не можем точно сказать сколько

предметов мыслиться в данном понятии); по

содержанию конкретным (мыслиться

совокупность предметов, как нечто

самостоятельно существующее),

положительным (характеризуется присуще

предметам свойство двигаться под действием

реактивной силы), безотносительным (мыслятся

предметы, существующие самостоятельно вне

зависимости от других предметов),

несобирательным (содержание данного понятия

можно отнести к каждому предмету мыслимому

в понятии).

Логическая характеристика понятий помогает

уточнить их содержание и объем, вырабатывает

навыки более точного употребления понятий в

процессе рассуждения.

8. Сравнимые и несравнимые понятия.

Понятия находятся между собой в

определенных отношениях. По содержанию между

понятиями могут быть только два вида отношений

— сравнимость и несравнимость. Далекие друг от

друга по своему содержанию понятия, не

имеющие общих признаков, называются

несравнимыми (безответственность и нитка,

романс и кирпич). Между ними невозможны

логические отношения.

Сравнимые понятия — это понятия, имеющие в

своем содержании общие, существенные признаки

(по которым они и сравниваются). Отношения

между понятиями изображают с помощью схем —

кругов Эйлера.

Между сравнимыми понятиями возможны два

вида отношений по объему: совместимость и

несовместимость, а сами соотносящиеся понятия

называются совместимыми или несовместимыми.

Совместимые понятия — это такие, объемы

которых полностью или частично совпадают.

Между совместимыми понятиями складываются

следующие отношения:

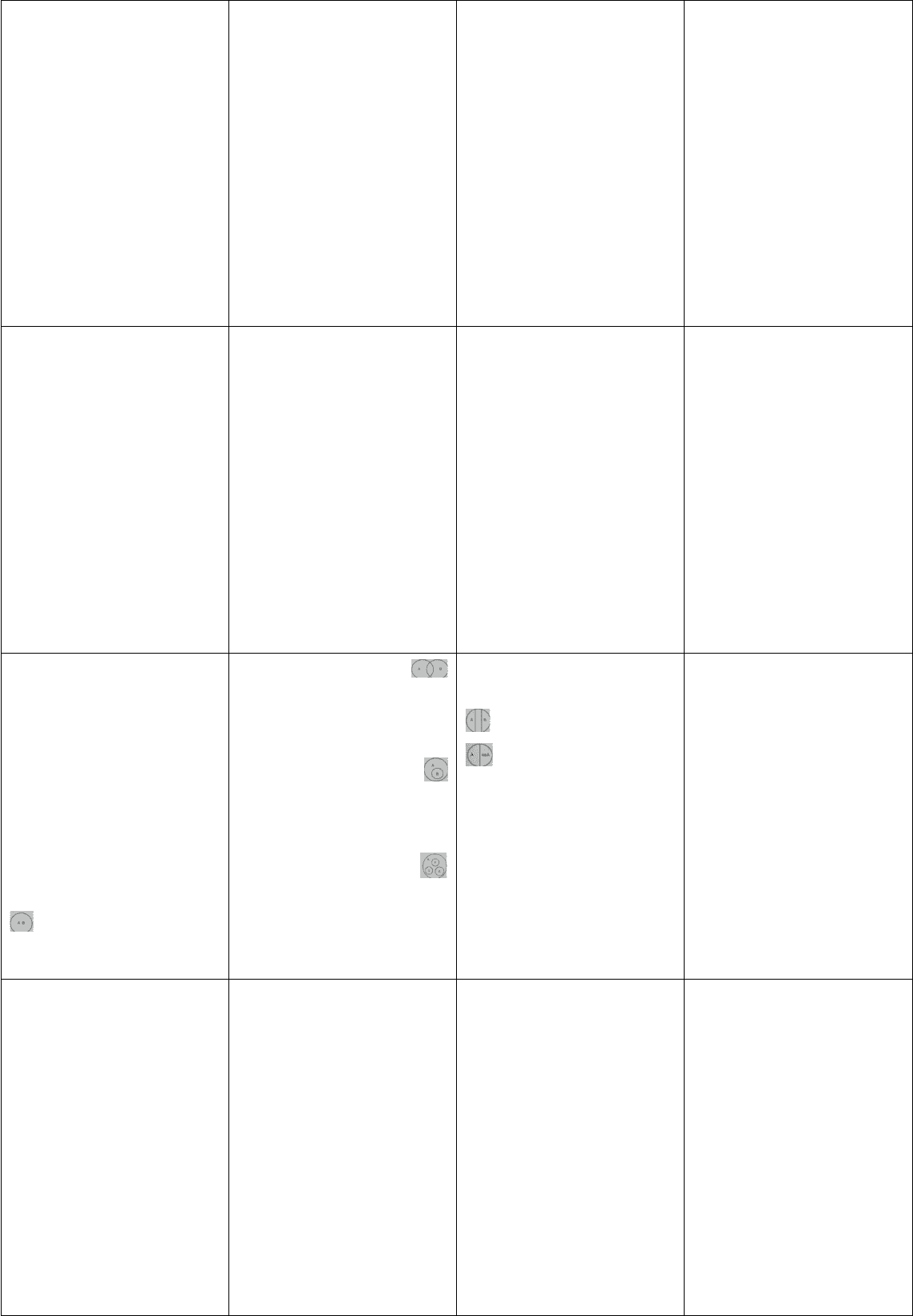
1 — равнообъемность

Равнообъемными или равнозначными

называются понятия, которые

различаются по своему содержанию, но объемы

которых совпадают.

2 — перекрещивание

Перекрещивающимися называются

понятия, объемы которых частично

совпадают, например «студент» и «спортсмен»,

«юрист» и «писатель». Они изображаются

пересекающимися кругами. В

перекрещивающейся части двух кругов мыслятся

студенты, являющиеся спортсменами. В левой

части круга мыслятся студенты, не являющиеся

спортсменами, а в правой части — спорт-

смены, не являющиеся студентами.

3 — подчинение

В отношении подчинения (субординации)

находятся понятия, если объем одного полностью

входит в объем другого, но не исчерпывает его.

Несовместимыми называются понятия, объемы

которых не совпадают. Несовместимые понятия

могут находиться между собой в следующих

отношениях.

1 — соподчинение

В отношении соподчинения

(координации) находятся понятия, объемы

которых исключают друг друга, но принадлежат

некоторому более общему родовому понятию.

2 — противоположность

В отношении противоположности

(контрарности) находятся два понятия, признаки

которых противоречат друг другу, а сумма их

объемов не исчерпывает родового понятия.

3 — противоречие

В отношении противоречия

(контрадикторности) находятся такие два

понятия, которые являются видами

одного и того же рода, и при этом одно

понятие указывает на некоторые

признаки, а другое эти признаки отрицает,

исключает, не заменяя их никакими другими

признаками.

9. Логические операции с понятиями.

Логическая операция обобщения понятий.

Обобщение объема А - логическая операция, в

результате которой образуется имя с объемом В,

содержащим в себе объем А. Иными словами,

обобщить имя А - значит образовать такое другое

имя В (род), которое подчиняло бы себе имя А

(вид).

На первый взгляд, обобщение - то же, что и

включение. Однако это не совсем так. Разница

прежде всего в том, что при обобщении более

общее имя В может быть в принципе неизвестным.

Его содержание надо еще выработать, объем

установить или уточнить, а само имя, быть может,

заново сформулировать, в то время как при

включении А в В эти имена выступают как

данные. Процессы обобщения - неотъемлемые

свойства научного познания. Прежде чем

появилось обобщающее имя «закон Бойля-

Мариотта», прошли десятилетия упорного труда

ученых по исследованию зависимости между

давлением и объемом различных газов.

В процессе познания обобщающее имя в свою

очередь может быть обобщено и т.д. Пределом

обобщения в каждом конкретном случае

выступает некое универсальное имя. В различных

науках - это имена, фиксирующие

фундаментальные понятия (научные категории):

точка, прямая, плоскость - в геометрии,

материальная точка,

масса, сила, ускорение - в механике; атом,

молекула, валентность - в химии; труд, товар,

деньги, стоимость - в экономической теории;

предмет, свойство, отношение - в логике.

Логическая операция ограничения понятий.

Ограничение - логическая операция, обратная

обобщению. Она состоит в нахождении имени с

объемом В, который содержится в объеме А.

Ограничить объем А - значит найти такое другое

имя В (вид), которое находилось бы в отношении

подчинения к А (роду). Пределом ограничения

выступают имена, объемы которых равны одному

предмету (единичные имена). Так, пределом

ограничения имени «столица» являются имена

отдельных государств: Минск, Москва, Токио и

т.д.

Особой разновидностью ограничения является

выделение типа, или типизация. Тип - это имя,

которому однородные предметы соответствуют в

той или иной мере. Если некоторые предметы

составляют объем имени А и среди них есть такие,

что безусловно (т.е. со степенью, равной 1)

принадлежат к объему В, а другие обладают этим

свойством в некоторой (меньшей) степени, то имя

с объемом В представляет собой тип. Так,

ограничивая объем имени «человек», можно

получить имя «высокий человек». Это будет тип,

поскольку, исходя из практики и разумных сооб-

ражений, можно выделить, безусловно, высоких

людей,

остальных же упорядочить по степени их

принадлежности к высоким людям, до той

границы, за которой находятся, безусловно,

невысокие люди (степень их принадлежности к

объему имени «высокий человек» равна 0). Тип,

таким образом, есть имя с нечетким объемом.

Присоединение к объему новых предметов,

тождественных со старыми по некоторому

признаку, называется логической операцией

расширения объема А.

Операция, обратная расширению, т.е. удаление

из объема А предметов, которые тождественны с

оставшимися по некоторым признакам, называется

локализацией объема имени А. Примером

локализации может служить произведенное в свое

время в биологии удаление китов из класса рыб,

хотя объем и содержание имени «рыба» остался

неизменным.

Логические операции с объемами имен не

следует смешивать с мысленными переходами от

части к целому и, наоборот, от целого к части.

Специфика последних наиболее отчетливо

выявляется при их сопоставлении с операциями

обобщения и ограничения.

Обобщаемое имя заключает в себе все содержа-

ние результата обобщения, но не наоборот. Иными

словами, вид обладает всеми признаками рода.

Например, можно, обобщив имя «газета»,

получить имя «периодическое издание», и ни одна

газета не мыслима без этого родового признака.

Иначе обстоит дело при переходе от части к це-

лому. Ознакомившись с отдельными

помещениями в новой квартире, можно составить

представление о квартире в целом, но нельзя

переносить свойства всей квартиры (например, то,

что она состоит из трех комнат), на каждую из

частей квартиры. Часть, таким образом, не

обладает содержанием целого (здесь имеется

аналогия с отношениями между собирательными и

несобирательными именами).

Поэтому смешение операции обобщения

(ограничения) с операцией мысленного перехода

от части к целому (от целого к части)

непозволительно и может служить источником

серьезных заблуждений. Например,

восточнославянское племя кривичей можно рас-

сматривать иногда как разновидность, иногда как

часть славян. В первом случае, зная, что

восточные славяне поклонялись Перуну, мы не

сделаем ошибки, заключив, что и кривичи

поклонялись Перуну (операция ограничения). Во

втором же случае из знания о том, что восточные

славяне подвергались набегам степняков, вовсе не

следует, что и любая их часть, например, кривичи,

подвергались этим набегам (переход от целого к

части). В противном случае допускается логиче-

ская ошибка.

10. Суждение как форма мышления.

Познавая объективный мир, человек

раскрывает связи между предметами и их

признаками, устанавливает отношения между

предметами, утверждает или отрицает факт

существования предмета. Эти связи и

отношения отражаются в мышлении в форме

суждений, представляющих собой связь

понятий. Связи и отношения выражаются в

суждении посредством утверждения или

отрицания. Всякое суждение может быть либо

истинным, либо ложным, т.е. соответствовать

действительности либо не соответствовать ей.

Если в суждении утверждается связь,

существующая в действительности, или

отрицается связь, которая в действительности

отсутствует, то такое суждение будет

истинным.

Суждение — это форма мышления, в

которой утверждается или отрицается связь

между предметом и его признаком, отношения

между предметами или факт существования

предмета; суждение может быть либо

истинным, либо ложным.

Языковой формой выражения суждения

является предложение. Подобно тому как

понятия не могут возникнуть и существовать

вне слов и словосочетаний, так и суждения не

могут возникнуть и существовать вне

предложений. Однако единство суждения и

предложения не означает их полного

совпадения. И если всякое суждение

выражается в предложении, то из этого не

следует, что всякое предложение выражает

суждение.

Суждение выражается повествовательным

предложением, в нем содержится сообщение о

чем-либо. вопросительные и побудительные

предложения суждений не выражают.

Суждение и предложение различаются по

своему составу. Суждение о связи предмета и

его признака состоит из двух понятий — двух

терминов суждения: субъекта, отражающего

предмет суждения, и предиката, отражающего

признак предмета. Субъект и предикат

обозначаются латинскими буквами S и Р.

Кроме субъекта и предиката суждение

включает в свой состав связку — элемент

суждения, который соединяет оба термина

суждения,

утверждая или отрицая принадлежность

предмету некоторого признака. Главные члены

предложения могут совпадать с субъектом и

предикатом суждения только в простом

нераспространенном двусоставном

предложении. Различие между суждением и

предложением состоит также в том, что

грамматический строй предложения в разных

языках различен.

Логическая же структура суждения

одинакова независимо от его выражения в том

или ином языке. Таким образом, суждение и

предложение образуют неразрывное единство,

но это единство включает в себя определенные

различия, которые необходимо учитывать, так

как отождествление суждения как формы

мышления и предложения как его языкового

выражения порождает ошибки в их анализе.

Суждения делятся на простые и сложные.

Простым называется суждение, не

включающее другие суждения. Суждение,

состоящее из нескольких простых суждений,

называется сложным.

11. Логическая структура простого

суждения (субъект, предикат, связка,

квантор).

Суждение — это форма мышления, в

которой утверждается или отрицается связь

между предметом и его признаком, отношения

между предметами или факт существования

предмета.

Атрибутивным называется суждение о

признаке предмета. В нем отражается связь

между предметом и его признаком, эта связь

утверждается или отрицается. Атрибутивные

суждения называют также категорическими.

Атрибутивное, или категорическое, суждение

состоит из субъекта, предиката и связки.

Субъектом суждения называется понятие о

предмете суждения и символически

обозначается символом - заглавной латинской

буквой «S».

Понятие о признаке предмета называется

предикатом суждения и символически

обозначается заглавной буквой «Р» латинского

алфавита.

Субъект и предикат называются терминами

суждения. Последний элемент суждения —

связка - выражает отношение между

субъектом и предикатом, между «S» и «Р».

Связка выразима в русском языке словами

«есть» - «не есть», «суть» - «не суть»,

«является» - «не является», «имеется» - «не

имеется» и пр. Этот элемент суждения в

русском языке зачастую просто опускается.

Так, вместо «Он есть добр» мы говорим «Он

добр», вместо «Дуб есть дерево» — «Дуб —

дерево» и т.п. Желательно выработать навык

перевода таких грамматических выражений в

адекватные им логические формы. Когда же

мы имеем дело с простыми суждениями

отношения или модальности, то роль связки

могут выполнять другие слова: «большее»,

«меньше», «равно», «справа», «слева»,

«лучше», «хуже», «было», «будет» и пр.

Используя символику, любое простое

категорическое суждение можно записать в

виде формулы «S—Р», где тире между

субъектом суждения «S» и предикатом «Р»

будет обозначать связку, логическую связь,

отношение между ними.

Кроме названных элементов в суждениях

имеется еще и не всегда явно выразимый, как

бы непостоянный, плавающий элемент,

отражающий количественную характеристику

субъекта суждения.

Этот логический оператор называется

"квантор" суждения. В языке он выражался

словами «все», «без исключения», «каждый» и

т.п. - квантор общности (всеобщности), или

словами «некоторые», «многие», «часть»,

«большинство» и др. - квантор существования.

Например: «Все S суть Р», «Некоторые S не

есть Р», «Часть S есть Р», «Большинство S не

есть Р» и т.п. В некоторых случаях квантор

лишь подразумевается, как в суждением

«Студенты нашей группы любят спорт»: тут не

ясно, все или некоторые студенты группы

любят спорт, а данное обстоятельство может

иметь существенное значение при дальнейшем

использовании и анализе суждения. Поэтому,

весьма важно уметь уточнять этот логический

показатель.

Символическое обозначение квантора

общности (всеобщности) — V, квантора

существования — I.

12. Виды простых суждений по объему, по

качеству связки, по содержанию предиката.

Простым называется суждение, выражающее связь

двух понятий или выраженное одним понятием, когда

второе подразумевается, лишь мыслиться. Например,

«Сидоров имеет высшее юридическое образование»,

«Ночь», «Моросит».

Простые суждения классифицируются по

следующим основаниям:

1.По качеству связки (по качеству). По качеству

суждения делятся на утвердительные и отрицательные.

Утвердительным называется суждение, выражающее

принадлежность предмету некоторого признака,

например: «Лицо, виновное в совершении

преступления, привлекается к уголовной

ответственности». Суждение, выражающее отсутствие

у предмета некоторого признака, называется

отрицательным. Утвердительное и отрицательное

суждения различаются характером связки, ее

качеством. Утвердительная связка («есть») указывает

на принадлежность признака предмету. Суждение с

отрицательным предикатом, но с утвердительной

связкой «S есть не-Р» рассматривается как

утвердительное.

2. По объему субъекта (по количеству) Утверждать или

отрицать что-либо можно об одном предмете, о части

предметов некоторого класса и обо всех предметах

класса. В соответствии с этим суждения по количеству

делятся на единичные, частные и общие. Единичным

называется суждение, в котором что-либо

утверждается или отрицается об одном предмете. Их

формула: «это S есть (не есть) P» Частным называется

суждение, в котором что-либо утверждается или

о части предметов некоторого класса. Частные

суждения выражаются в предложениях, имеющих в

своем составе слова: «некоторые», «многие»,

«немногие», «большинство», «меньшинство», «часть».

В неопределенном частном суждении слово

«некоторые» употребляется в значении «Некоторые, а

может быть, и все», «по крайней мере, некоторые».

Оно имеет такую формулу: «Некоторые S есть (не есть)

P», квантор «некоторые» придает ему

неопределенность. В определенном частном суждении

слово «некоторые» употребляется в значении «только

некоторые», имеет такую формулу: «Только некоторые

S есть (не есть) P». Общим называется суждение, в

котором что-либо утверждается или отрицается обо

всех предметах некоторого класса. В отличие от

единичных суждений частные суждения содержат

обобщенные знания. В неопределенном частном

суждении эти знания характеризуются

незавершенностью. Знания, содержащиеся в общих

суждениях, характеризуются общностью и

завершенностью. В общих суждениях выражаются

законы науки, законы, устанавливаемые государством,

правовые нормы и т.д. Их формула: «Все S есть P»,

«Ни одно S не есть P», например: «Каждая страна

имеет свой гимн» - является общим суждением, т.к.

объем субъекта включает весь класс отображаемых

предметов

3. По содержанию предиката. Суждение делиться на

суждение свойств (атрибутивное), суждение

отношения (релятивное) и суждение существования

(экзистенциальное):

1.Суждение свойства: отражает принадлежность или

не принадлежность предмету мысли того или иного

свойства, состояния. например.: «Никто из судей не

вправе воздерживаться от голосований». 2. суждение

отношения: выражает различные связи между

предметами мысли по месту, времени, причинной

зависимости, например, «Саратов расположен севернее

Волгограда». 3. Суждение существования указывает на

факт наличия или отсутствия того или иного предмета

мысли, например, «Не существует беспричинных

явлений» В классической логике также различают

категорическое суждение, в котором отношения между

субъектом и предикатом выражается вполне

определенно, без формулировки каких либо условий и

без каких-либо вариантов. Обычно к категорическим

относятся все атрибутивные суждения. Таковы

основные виды простых суждений. Любое суждение

имеет количественную и качественную

определенность. Поэтому в логике применяется

объединенная классификация суждений по количеству

и по качеству. В результате получаем 4 вида суждений:

общеутвердительные, общеотрицательные,

частноутвердительные, частноотрицательные.

Общеутвердительное суждение — это суждение,

общее по количеству и утвердительное по качеству, его

логическая структура: «Все S суть Р», например: «Все

школьники являются учащимися». Эти суждения

обозначаются в логике латинской буквой А.

Общеотрицательное суждение — суждение, общее по

количеству и отрицательное по качеству, его

логическая структура «Ни одно S не есть Р»,

например: «Все планеты не являются звездами»

(или «Ни одна планета не является звездой»). Такие

суждения обозначаются латинской буквой Е.

Частноутвердительное суждение — суждение,

частное по количеству и утвердительное по качеству,

его логическая структура: «Некоторые S суть Р»,

например: «Некоторые животные являются

хищниками». Эти суждения обозначаются латинской

буквой I.

Частноотрцательное суждение — суждение, частное

по количеству и отрицательное по качеству, его

логическая структура: «Некоторые S не суть Р»,

например: «Некоторые грибы не являются

съедобными». Эти суждения обозначаются латинской

буквой О.

Особое место в классификации суждений занимают

1) выделяющие и 2) исключающие суждения.

Выделяющие суждения они отражают тот факт, что

признак, выраженный предикатом, принадлежит (или

не принадлежит) только данному, и никакому другому,

предмету. «Некоторые города — столицы государств»

— пример частного выделяющего суждения

(некоторые 8, и только S, суть Р). Столицами

государств могут быть только города, и притом только

некоторая их часть. Предикат частного выделяющего

суждения полностью входит в объем субъекта.

Исключающим называется суждение, в котором

отражается принадлежность (или непринадлежность)

признака всем предметам, за исключением некоторой

их части. Например: «Все студенты нашей группы,

кроме Волкова, сдали экзамены». Исключающие

суждения выражаются предложениями со словами

«кроме», «за исключением», «помимо», «не считая» и

13. Виды сложных суждений в соответствии с

функциями логических связок.

Сложные суждeния образуются из нескольких

простых суждений.

Так же, как и простые, сложные суждения

могут быть истинными или ложными. Но в

отличие от простых суждений, истинность или

ложность которых определяется их соответствием

или несоответствием действительности,

истинность или ложность сложного суждения

зависит прежде всего от истинности или ложности

составляющих его суждений.

Логическая структура сложных суждений также

отличается от структуры простых суждений.

Основными структурообразующими элементами

здесь являются уже не понятия, а простые

суждения, составляющие сложное суждение. При

этом связь между ними осуществляется не с

помощью связок «есть», «не есть» и т. п., а

посредством логических союзов «и», «или»,

«либо», «если [...], то» и др. Юридическая

практика особенно богата такого рода

суждениями.

В соответствии с функциями логических связок

сложные суждения делятся на следующие виды.

Соединительные суждения (конъюнктивные) - это

такие суждения, которые включают в качестве

составных частей другие суждения - конъюнкты,

объединяемые связкой «и». Например,

«Осуществление прав и свобод человека и

должно нарушать права и свободы других лиц».

Разделительные (дизъюнктивные) суждения -

включают в качестве составных частей суждения -

дизъюнкты, объединяемые связкой «или».

Например, «Истец вправе увеличить или

уменьшить размер исковых требований».

Различают слабую дизъюнкцию, когда союз

«или» имеет соединительно-разделительное

значение, то есть входящие в сложное суждение

составляющие не исключают друг друга.

Например, «Договор купли-продажи может быть

заключен в устной или письменной форме».

Сильная дизъюнкция возникает, как правило,

тогда, когда логические союзы «или», «либо»

употребляются в исключающе-разделяющем

смысле, то есть ее составляющие исключают друг

друга. Например, «Клевета, соединенная с

обвинением лица в совершении тяжкого или особо

тяжкого преступления, наказывается

ограничением свободы на срок до трех лет, либо

арестом на срок от четырех до шести месяцев,

либо лишением свободы на срок до трех лет».

Условные (импликативные) суждения образованы

из двух простых суждений посредствам

логического союза «если [...], то». Например,

«Если по истечении срока временной работы с

работником не был расторгнут договор, то он

считается принятым на постоянную работу».

Аргумент, начинающийся в импликативных

суждениях словом «если», называется

основанием, а составляющая, начинающаяся со

слова «то» - следствием.

Сложные суждения, рассмотренные из

методических соображений по отдельности, в

реальном процессе мышления используются в

различном сочетании друг с другом, образуя порой

весьма сложные мыслительные конструкции.

Например: «Суд не принимает отказа истца от

иска, признание иска ответчиком и не утверждает

мирового соглашения сторон, если эти действия

противоречат закону и нарушают чьи-либо права и

охраняемые законом интересы». Здесь налицо

соединение нескольких конъюнкций с

дизъюнкцией и импликацией.

14. Виды сложных суждений по количеству

терминов.

а) Соединительные (конъюнктивные) суждения

Сложным называют суждение, состоящее из не-

скольких простых, связанных логическими

связками. Различают следующие виды сложных

суждений: 1) соединительные, 2) разделительные,

3) условные, 4) эквивалентные. Истинность таких

сложных суждений определяется истинностью

составляющих их простых.

А. Соединительные (конъюнктивные)

суждения. Соединительным, или конъюнктивным,

называют суждение, состоящее из нескольких

простых, связанных логической связкой «и».

Например, суждение «Кража и мошенничество

относятся к умышленным преступлениям»

является соединительным суждением, состоящим

из двух простых: «Кража относится к

умышленным преступлениям», «Мошенничество

относится к умышленным преступлениям».

символически можно выразить как р /\ q, где р и q

— члены конъюнкции (или конъюнкты), л —

символ конъюнкции.

Соединительное суждение может быть

выражено одной из трех структур.

Два субъекта и один предикат (S' и S" есть Р).

Например, «Конфискация имущества и лишение

звания являются дополнительными уголовно-

правовыми санкциями».

Один субъект и два предиката (S есть Р' и Р").

Например, «Преступление — это общественно

опасное и противоправное деяние».

Два субъекта и два предиката (S' и S" есть Р' и

Р"). Например, «Основные права и свободы

человека неотчуждаемы и принадлежат каждому

от рождения».

Истинность соединительного суждения

определяется истинностью входящих в него

простых суждений. Соединительное суждение

истинно только в том случае, если истинны

простые его составляющие. Если хотя бы одно

простое суждение ложно, то ложным является и

конъюнкция в целом.

Б. Разделительные суждения

Разделительным, или дизъюнктивным,

называют суждение, состоящее из нескольких

простых, связанных логической связкой «или».

Например, суждение «Договор купли-продажи

может быть заключен в устной или письменной

форме» является разделительным суждением,

состоящим из двух простых. Если первое

обозначить р, а второе — q, то разделительное

суждение символически можно выразить как р v g,

где р и q — члены дизъюнкции (дизъюнкты), v —

символ дизъюнкции.

Разделительное суждение может быть как

двух-, так и многосоставным: р v q ... v n.

В языке разделительное суждение может быть

выражено одной из трех логико-грамматических

структур.

Два субъекта и один предикат (S' или S" есть Р).

Например, «Хищение в крупных размерах или

совершенное группой лиц имеет повышенную

общественную опасность».

Один субъект и два предиката (S есть Р' или Р").

Например, «Хищение наказывается

исправительными работами или тюремным

заключением».

Два субъекта и два предиката (Sf или S" есть Р'

или Р"). Например, «Ссылка или высылка могут

применяться в качестве основной или

дополнительной санкции».

В. Условные суждения

Условным, или импликативным, называют

суждение, состоящее из двух простых, связанных

логической связкой «если.., то...». Например:

«Если предохранитель плавится, то электролампа

гаснет». Первое суждение — «Предохранитель

плавится» называют антецедентом

(предшествующим), второе — «Электролампа

гаснет» — консеквентом (последующим). Если

антецедент обозначить р, консеквент — q, а связку

«если..., то...» знаком « ->», то импликативное

суждение символически можно выразить как ( р ->

q ).

Г. Эквивалентные суждения

Эквивалентным называют суждение,

включающее в качестве составных два суждения,

связанных двойной (прямой и обратной) условной

зависимостью, выражаемой логической связкой

«если и только если.., то...». Например: «Если и

только если человек награжден орденами и

медалями (р), то он имеет право на ношение

соответствующих орденских планок (q)».

Логическая характеристика этого суждения

состоит в том, что истинность утверждения о

награждении (р) рассматривается как необходимое

и достаточное условие истинности утверждения о

наличии права на ношение орденских планок (q).

Точно так же истинность утверждения о наличии

права на ношение орденских планок (q) является

необходимым и достаточным условием истин-

ности утверждения о том, что данное лицо

награждено соответствующими орденом или

медалью (р). Такую обоюдную зависимость

символически можно выразить двойной

импликацией р *-> q, которая читается: «Если и

только если р, то q». Эквивалентность выражают и

другим знаком: р = q.

В естественном языке, в том числе и в

юридических текстах, для выражения

эквивалентных суждений используют союзы:

«лишь при условии что.., то...», «в том и только в

том случае когда.., тог

да...», «только тогда когда..,

то...» и др.

15. Виды сравнимых Aсуждений:

совместимые и несовместимые.

Основу отношений между суждениями

составляет их сходство по содержанию,

выражаемое в таких логических характеристиках,

как смысл и истинность суждений. В соответствии

с этим логические отношения устанавливаются не

между любыми, а лишь между сравнимыми

суждениями, то есть теми, которые имеют общий

смысл.

Сравнимые суждения делятся на совместимые и

несовместимые. Совместимыми являются

суждения, которые одновременно могут быть

истинными. Различают три вида совместимости.

1. Эквивалентные суждения выражают одну и

ту же мысль в различной форме. Например,

«Водитель автомобиля совершил аварию» и

«Причина аварии заключается в действиях

водителя автомобиля».

2. Частичная совместимость характерна для

суждений, которые могут быть одновременно

истинными, но не могут быть одновременно

ложными. Например, «Некоторые свидетели

правдивы» и «Некоторые свидетели не являются

правдивыми».

3. Отношения подчинения характерны для

суждений, которые имеют общий предикат, а

понятия, выражающие субъекты двух таких

суждений, находятся в отношении логического

подчинения. Например, «Ни один вопрос

оставаться без ответа» и «Некоторые вопросы

обучаемого не должны оставаться без ответа». В

данном случае первое суждение будет

подчиняющим, а второе - подчиненным. При

истинности подчиняющего подчиненное всегда

будет истинным. А в целом для них характерны

следующие зависимости:

- при истинности общего суждения частное всегда

будет истинным;

- при ложности частного суждения общее

суждение также будет ложным;

- при ложности общего суждения частное

неопределенно;

- при истинности подчиненного частного

суждения общее неопределенно.

Перейдем к рассмотрению отношений между

несовместимыми суждениями. Несовместимыми

являются суждения, которые одновременно не

могут быть истинными. Различают два вида

несовместимости.

1. Несовместимость как противоположность

характерна для суждений, выражающих

противоположные мысли. Эти суждения не могут

быть одно¬временно истинными, но могут быть

одновременно ложными. Например, «Все

адвокаты юристы», «Ни один адвокат не является

юристом».

Истинность одного из противоположных

суждений определяет ложность другого. К

примеру, истинность суждения «Все граждане

соблюдать закон» сразу же делает ложным

суждение «Ни один гражданин не обязан

соблюдать закон». При ложности одного из

противоположных суждений другое остается

неопределенным. Оно может быть как истинным,

так и ложным.

2. Противоречие как несовместимость

характерно для суждений, исключающих друг

друга. Они одновременно не могут быть ни

истинными, ни ложными. При истинности одного

из них другое будет ложным, а при ложности

первого второе будет истинным. Например, «Все

судьи являются подкупными» и «Некоторые судьи

не являются подкупными».

16. Логические отношения между

несовместимыми простыми суждениями.

Логические отношения складываются

между такими вещами, как понятия и

суждения. Понятие - это такая логическая

операция, в ходе которой человек

определяет значение чего-либо, сравнивает

и отличает предметы один от другого.

Логическая форма понятий - это способ

связи признаков предметов с самими

предметами. Суждение же представляет

собой некую мысль, в которой

утверждается наличие или отсутствие

каких-либо ситуаций или связей между

ситуациями. Суждение обычно выражается

повествовательным предложением. Таким

образом, логическая форма суждений - это

способ связи понятий о предмете,

свойствах предметов или отношений

между предметами, выраженный в форме

утверждения или отрицания. Существует

также способ связи этих суждений, или

логическая форма умозаключения.

Видами отношений между суждениями по

логическим формам являются:

1. Совместимость по истине

По своей истине суждения могут быть

совместимыми и несовместимыми.

2. Совместимость по ложности

По данному признаку суждения также

могут быть совместимыми и

несовместимыми.

3. Логическое следование

4. Логическая эквивалентность

5. Подчинение

6. Противоречие (контрадикторность)

7. Контрарность

8. Субконтрарность

9. Логическая независимость.

17. Логический квадрат как модель

отношений между простыми категорическими

суждениями.

Отношения между простыми суждениями. +

Условия истинности простых суждений по

логическому квадрату.

Основу отношений между суждениями

составляет их сходство по смыслу и логическим

значениям (истинности и ложности). В силу этого

отношения устанавливаются не между любыми, а

лишь между сравнимыми, т.е. имеющими общий

смысл суждениями.

Несравнимыми являются суждения, имеющие

различные субъекты или предикаты. Таковы,

например, два суждения: «Среди космонавтов есть

летчики»; «Среди космонавтов есть женщины».

Сравнимыми являются суждения с

одинаковыми субъектами и предикатами и

различающиеся связкой или квантором. Например:

«Все американские индейцы живут в резерваци-

ях»; «Некоторые американские индейцы не живут

в резервациях».

Отношения между простыми суждениями

обычно рассматриваются с помощью

мнемонической схемы, называемой логическим

квадратом. Его вершины

символизируют простые

категорические суждения — А, Е, I, 0;

стороны и диагонали — отношения

между суждениями.

Среди сравнимых различают совместимые и

несовместимые суждения.

Совместимыми являются суждения, которые

одновременно могут быть истинными. Различают

три вида совместимости: эквивалентность (полная

совместимость), частичная совместимость

(субконтрарность) и подчинение.

1. Эквивалентными являются такие суждения,

которые имеют одинаковые логические

характеристики: одинаковые субъекты и

предикаты, однотипную — утвердительную или

отрицательную — связку, одну и туже

выраженную квантором количественную

характеристику. С помощью логического квадрата

отношения между простыми эквивалентными

суждениями не иллюстрируются.

2. Частичная совместимость характерна для

суждений I и О, которые могут быть

одновременно истинными, но не могут быть

одновременно ложными.

При ложности одного из них другое будет

истинным: 11 -» О, 10 -»I. Например, при

ложности суждения «Некоторые злаки ядовиты»

будет истинным суждение «Некоторые злаки не

являются ядовитыми». В то же время при

истинности одного из частных суждений другое

может быть как истинным, так я ложным: I -> (О v

1 О); 0"»(<lvll).

3. Подчинение имеет место между суждениями

А и I, Е и О. Для них характерны следующие две

зависимости.

При истинности общего суждения частное

всегда будет истинным: А —> I, E -» О. Например,

при истинности общего суждения «Всякое

правоотношение регулируется нормами права»

истинным будет и частное — «Некоторые

правоотношения регулируются нормами права».

При истинности суждения «Ни один кооператив

не относится к государственным организациям»

будет истинным и суждение «Некоторые

кооперативы не относятся к государственным

организациям».

При ложности частного суждения общее

суждение также будет ложным: 11 -> ] А; 10 ->] Е.

При подчинении остаются неопределенными

следующие зависимости, при ложности общего

суждения подчиненное частное может быть как

истинным, так и ложным: ! А -> (I v ] I); 1Е ~»(О

v ] О); при истинности подчиненного частного

общее может быть как истинным, так и ложным. I

-> (A v 1 А); О -»(Е v IE).

Несовместимыми являются суждения А и Е, А и

О, Е и I, которые одновременно не могут быть

истинными. Различают два вида несовместимости:

противоположность и противоречие. .

1. Противоположными (контрарными) являются

суждения А и Е, которые одновременно не могут

быть истинными, но могут быть одновременно

ложными.

Истинность одного из противоположных

суждений определяет ложность другого: А —> 1

Е; Е -> I А.

Например, истинность суждения «Все офицеры

— военнослужащие» определяет ложность

суждения «Ни один офицер не является

военнослужащим». При ложности же одного из

противоположных суждений другое остается

неопределенным — оно может быть как

истинным, так и ложным: ] А -> (Е v 1 Е); 1 Е -> (A

v I A).

2. Противоречащими (контрадикторными)

являются суждения А и О, Е и I, которые

одновременно не могут быть ни истинными, ни

ложными.

Для противоречия характерна строгая, или

альтернативная, несовместимость: при истинности

одного из суждений другое всегда будет ложным;

при ложности первого второе будет истинным.

Отношения между такими суждениями

регулируются законом исключенного третьего.

Если А признается истинным, то О будет

ложным (А -> 10); при истинности Е будет

ложным I: (Е -> 1 I). И наоборот: при ложно

сти А

будет истинным О (1А -> О); а при ложности Е

будет истинным I (| Е -> I).

18. Логика вопросов и ответов. Роль вопроса

в познании социальных явлений.

Развитие научных и практических знаний

протекает как переход от ранее установленных

суждений к новым, более точным и богатым по

содержанию. Этот переход представляет собой

последовательность следующих этапов: 1)

постановка вопроса, 2) поиски новой информации

в определенной области, 3) конструирование

ответа на поставленный вопрос.

Грамматической формой вопроса является

вопросительное предложение. Вопрос — это

выраженная в вопросительном предложении

мысль, направленная на уточнение или

дополнение знаний. В процессе познания вопросы

не возникают самопроизвольно, без всяких на то

оснований. Любой вопрос всегда опирается на уже

известное знание, которое выступает его базисом,

выполняя роль предпосылки вопроса.

Познавательная функция вопроса реализуется в

форме ответа на поставленный вопрос. Ответ —

новое суждение, уточняющее или дополняющее в

соответствии с поставленным вопросом прежнее

знание. Поиск ответа предполагает обращение к

конкретной области теоретических или

эмпирических знаний, которую называют

областью поиска ответов. Полученное в ответе

знание, расширяя либо уточняя исходную

информацию, может служить базисом для

постановки новых, более

глубоких вопросов о предмете исследования.

Постановка вопроса и поиск информации для

ответа составляют явно или неявно присущую

любому познавательному процессу вопросно-

ответную форму развития знаний. Она всегда

выступает направляющим началом в развитии

естествознания и техники. Родоначальник

индуктивной логики Френсис Бэкон говорил, что

мы должны уметь задавать вопросы природе.

Таким же путем приобретается исходная

информация в социологии, экономике,

правоведении, медицине и других областях.

Особая роль принадлежит вопросно-ответной

форме в процессе судопроизводства. Поиск

ответов на интересующие следствие и суд вопросы

составляет основное содержание допросов,

следственных экспериментов,

освидетельствований, очных ставок и многих

других следственных действий. В

судопроизводстве вопросно-ответная форма

служит процессуально-правовым алгоритмом,

определяющим основные направления, важнейшие

позиции и пределы судебного исследования по

уголовным и гражданским делам. В качестве

примера приведем предусмотренную Уголовно-

процессуальным Кодексом Российской Федерации

последовательность вопросов, разрешаемых судом

при постановлении приговора (ст. 303 УПК РФ).

«При постановлении приговора суд в

совещательной комнате разрешает следующие

вопросы:

1) имело ли место деяние, в совершении

которого обвиняется подсудимый;

2) содержит ли это деяние состав преступления

и каким именно уголовным законом оно

предусмотрено;

3) совершил ли это деяние подсудимый;

4) виновен ли подсудимый в совершении этого

преступления;

5) подлежит ли подсудимый наказанию за

совершенное им преступление;

6) какое именно наказание должно быть

назначено подсудимому и подлежит ли оно

отбытию

подсудимым...»

Далее в УПК РФ перечисляются еще пять

подлежащих разрешению вопросов, касающихся:

признания подсудимого особо опасным

рецидивистом; удовлетворения гражданского

иска; судьбы вещественных доказательств;

судебных издержек и меры пресечения в

отношении подсудимого.

УПК РФ предусматривает также: вопросы,

подлежащие разрешению прокурором по делу,

поступившему с обвинительным заключением (ст.

213 УПК РФ); вопросы, подлежащие выяснению

при предании обвиняемого суду (ст. 222 УПК РФ);

вопросы, разрешаемые судом при вынесении

определения о применении принудительных мер

медицинского характера (ст. 409 УПК РФ).

20. Виды вопросов. Правила постановки

вопросов.

Вопрос - это выраженный в форме

вопросительного предложения и реализуемый в

виде ответа запрос мысли, направленный на

развитие - уточнение или дополнение знаний.

В процессе познания вопросы не возникают

самостоятельно, без всяких на то оснований.

Любой вопрос всегда опирается на уже известное

знание, которое выступает его базисом и

выполняет роль предпосылки вопроса.

Познавательная функция вопроса реализуется в

форме ответа на поставленный вопрос. Ответ

представляет собой новое суждение, уточняющее

или дополняющее в соответствии с поставленным

вопросом прежнее знание. Поиск ответа

предполагает обращение к конкретной области

теоретических или эмпирических знаний, которую

называют областью поиска ответа. Полученное в

ответе знание, расширяя либо уточняя исходную

информацию, может служить базисом для

постановки новых, более глубоких вопросов о

предмете исследования.

Существуют различные по структуре и

функциям вопросы. Среди них:

Корректные и некорректные. В отличие от

суждения вопрос не содержит ни утверждения, ни

отрицания, поэтому выраженную в нем

информацию не оценивают в терминах истины и

лжи, т.е.

о вопросе не говорят как об истинном или

ложном. Вместе с тем вопрос явно или неявно

опирается на определенное исходное, или

базисное знание, выступающее предпосылкой

вопроса. Качество базисного знания существенно

влияет на логический статус вопроса, определяя

правильность и неправильность постановки

вопроса. Правильно поставленным считается

вопрос, предпосылка которого представляет собой

истинное и непротиворечивое знание.

Неправильно поставленным считается вопрос с

ложным или противоречивым базисом. Примером

неправильно поставленного может быть

следующий вопрос: “Какой размер обуви у

снежного человека?” Предпосылка этого вопроса

включает отнюдь не бесспорную идею о

существовании снежного человека. О таком

вопросе говорят как о неправильно, или

некорректно поставленном - прежде чем выяснять

размер обуви снежного человека, следует

установить факт существования снежного

человека. В том случае, когда неправильно

поставленный вопрос умышленно используется с

целью запутать отвечающего, такой вопрос

квалифицируют как улавливающий, или

“провокационный”.

Вопросы могут быть закрытыми и открытыми.

Открытые вопросы предполагают возможность

неограниченного количества ответов.

Закрытые вопросы - это вопросы, на которые

возможно дать ограниченное количество

ответов. Такие вопросы чаще всего используют во

время социологических опросов. Например,

вопрос “Как Вы относитесь к деятельности

Государственной налоговой администрации

Украины?” является открытым, потому что

человек может высказывать свое собственное

мнение по этому поводу.

По логической структуре и познавательной

функции вопросы подразделяются на два

основных типа: уточняющие (ли-вопросы) и

восполняющие.

Уточняющим называется вопрос, направленный

на выявление истинности выраженного в нем

суждения. Например: “Верно ли, что Земля вращается

вокруг Солнца?”

Грамматический признак уточняющих

вопросов - наличие в предложении частицы “ли”:

“Верно ли, что...”; “Является ли ...”; “Так ли, что...”;

“Действительно ли, что...” и другие синонимные

выражения.

Восполняющим называется вопрос,

направленный на выявление новых свойств у

исследуемых явлений: “Где состоялся Всемирный

чемпионат по футболу 1998 года?”

Грамматический признак восполняющих

вопросов - наличие в предложении

вопросительных слов: кто? что? где? когда? как? и

других, с помощью которых стремятся получить

дополнительную информацию о том, что собой

представляет исследуемый объект.

Как уточняющие, так и восполняющие вопросы

могут быть простыми и сложными. Простым

называется вопрос, не включающий в качестве

составных частей других вопросов. Сложным

называется вопрос, включающий в качестве составных

частей другие вопросы, объединяемые логическими

связками.

По отношению к познавательной цели вопросы

делятся на узловые и восполняющие. Узловые – если

верный ответ служит для достижения цели («что такое

логическая характеристика?») Наводящие –

подогавливают человека к пониманию узлового

вопроса.

Познавательная функция вопроса реализуется в

форме вновь полученного суждения - ответа на

поставленный вопрос. При этом по содержанию и

структуре ответ должен строиться в соответствии с

поставленным вопросом. Лишь в этом случае ответ

расценивается как релевантный, т.е. как ответ по

существу поставленного вопроса, выполняющий свое

основное назначение - уточнить неясную или

неопределенную и доставить новую информацию.

Если в качестве ответа приводят хотя и истинные,

но содержательно не связанные с вопросом суждения,

то их расценивают как ответы не по существу вопроса

и обычно исключают из рассмотрения. Появление

таких вопросов в дискуссии или в процессе допроса -

либо результат заблуждения, когда отвечающий не

уловил смысл вопроса, но пытается отвечать на него,

либо сознательное стремление уйти от невыгодного

ответа на поставленный вопрос.

21. Логическая сущность ответа. Виды

ответов. Правила формулировки ответов.

Среди ответов различают:

- истинные и ложные;

- прямые и косвенные;

- краткие и развернутые;

- полные и неполные.

По отношению к действительности, ответы

могут быть истинными и ложными. Ответ

расценивается как истинный, если выраженное в

нем суждение правильно, или адекватно отражает

действительность. Ответ расценивается как

ложный, если выраженное в нем суждение

неверно, или неадекватно отражает положение дел

в действительности.

Прямые и косвенные ответы - это два вида

ответов, различающихся способом выражения

информации.

Прямым называется ответ взятый

непосредственно из области поиска ответов, при

конструировании которого не прибегают к

дополнительным сведениям и рассуждениям.

Например, прямым ответом на восполняющий

вопрос “Когда была принята Конституция

Украины?” будет суждение: “Конституция

Украины была принята 28 июня 1996 года”.

Прямым ответом на уточняющий вопрос -

“Является ли дельфин рыбой?” будет суждение:

“Нет, дельфин не является рыбой”.

Косвенным называется ответ, который берут из

более широкой области, нежели область поиска

ответа, и из которого лишь выводным путем

можно получить прямой ответ. Так, для вопроса

“Когда была принята Конституция Украины?”

косвенным будет следующий ответ: ”Конституция

Украины была принята накануне 5-ой годовщины

независимости Украины”. На вопрос “Является ли

дельфин рыбой?” косвенным будет ответ:

“Дельфин относится к млекопитающим

животным”.

По грамматической форме ответы могут быть

краткими и развернутыми.

Краткие - это односложные - утвердительный и

отрицательный ответы: “да” или “нет”.

Развернутые - это ответы, в каждом из которых

повторяются все элементы вопроса.

Краткие ответы наиболее подходящие для

простых вопросов; при сложных вопросах

целесообразно пользоваться развернутыми

ответами, поскольку односложные ответы в этом

случае нередко оказываются двусмысленными.

По объему представленной в ответе

информации они могут быть полными или

неполными. Проблема полноты чаще всего

возникает при ответах на сложные вопросы.

Полный ответ включает информацию по всем

элементам или составным частям вопроса.

Неполный ответ включает информацию

относительно лишь отдельных элементов или

составных частей вопроса.

Логическая зависимость между вопросом и

ответом означает, что качество ответа во многом

определяется качеством вопроса. Не случайно в

полемике и в процессе допроса действует правило:

каков вопрос, таков ответ. Это значит, что на

расплывчатый и двусмысленный вопрос трудно

получить ясный ответ; если хочешь получить

точный и определенный ответ, то сформулируй

точный и определенный вопрос.

Под точностью и определенностью в данном

случае имеется в виду логическая, т.е. понятийно-

структурная характеристика вопроса. Она

выражается в точности употребляемых понятий и

вопросительных слов, а также в рациональном

использовании сложных вопросов.

Точность ответа на восполняющий вопрос

зависит от степени определенности

вопросительных слов - кто? что? где? когда? как?

и т.п., которые сами по себе не отличаются

достаточной точностью.

Неопределенность в ответе возникает в случае

краткого утверждения на дизъюнктивный вопрос.

Например, если на вопрос “Курение вредно или

аморально?” ответить “Да”, то не ясно что имеется

в виду:

- Курение и вредно и аморально;

- Курение вредно, но не аморально;

- Курение не вредно, но аморально.

Неопределенность кратких ответов снимается в

первом случае - развернутым отрицательным, а во

втором - развернутым утвердительным ответами.

Знание логического механизма постановки

вопросов и конструирования ответов на них играет

важную роль уголовном процессе, служит

рациональной основой успешного проведения

допросов, свидетельствований, опознания и

других судебно-следственных действий, а также

продуктивных социологических опросов путем

анкетирования.

22. Общая характеристика

умозаключения. Логическая структура

умозаключения.

Умозаключение — это форма мышления,

посредством которой из одного или

нескольких суждений выводится новое

суждение.

Любое умозаключение состоит из посылок,

заключения и вывода. Посылками

умозаключения называют исходные суждения,

из которых выводится новое суждение.

Заключением называется новое суждение,

полученное логическим путем из посылок.

Логический переход от посылок к заключению

называется выводом.

Например: «Судья не может участвовать в

рассмотрении дела, если он является

потерпевшим (1). Судья Н. — потерпевший

(2). Значит, он не может участвовать в

рассмотрении дела (3)».

В этом умозаключении 1-е и 2-е суждения

являются посылками, 3-е суждение —

заключением.

При анализе умозаключения посылки и

заключение принято записывать отдельно,

располагая их друг под другом. Заключение

записывают под горизонтальной чертой,

отделяющей его от посылок и обозначающей

Слова «следовательно» и близкие ему по

смыслу («значит», «поэтому» и т.п.) под чер-

той обычно не пишутся. В соответствии с этим

приведенный пример примет следующий вид:

Судья не может участвовать в рассмотрении

дела, если он является потерпевшим.

Судья Н. — потерпевший.

Судья Н. не может участвовать в

рассмотрении дела.

Отношения логического следования между

посылками и заключением предполагает связь

между посылками по содержанию. Если

суждения не связаны по содержанию, то вывод

из них невозможен. При наличии

содержательной связи между посылками мы

можем получить в процессе рассуждения

новое истинное знание при соблюдении двух

условий: во-первых, исходные суждения —

посылки умозаключения должны быть

истинными; во-вторых, в процессе

рассуждения следует соблюдать правила

вывода, которые обусловливают логическую

правильность умозаключения.

Умозаключения делятся на следующие виды.

1. В зависимости от строгости правил

вывода различают демонстративные

(необходимые) и недемонстративные

(правдоподобные) умозаключения.

Демонстративные умозаключения

характеризуются тем, что заключение в них с

необходимостью следует из посылок, т. е.

логическое следование в такого рода выводах

представляет собой логический закон. В

недемонстративных умозаключениях правила

вывода обеспечивают лишь вероятностное

следование заключения из посылок.

2. По характеру связи между знанием

различной степени общности, выраженному в

посылках и заключении, различают три вида

умозаключений: дедуктивные (от общего

знания к частному), индуктивные (от частного

знания к общему), умозаключения по аналогии

(от частного знания к частному).

23. Дедукция. Виды, особенности и состав

дедуктивных умозаключений.

Общая характеристика дедуктивного

умозаключения.

В процессе познания действительности мы

приобретаем новые знания. Некоторые из них —

непосредственно, в результате воздействия

предметов внешнего мира на органы чувств. Но

большую часть знаний мы получаем путем

выведения новых знаний из знаний уже

имеющихся. Эти знания называются

опосредствованными, или выводными. Логической

формой получения выводных знаний является

умозаключение.

Умозаключение — это форма мышления,

посредством которой из одного или нескольких

суждений выводится новое суждение. Любое

умозаключение состоит из посылок, заключения и

вывода. Посылками умозаключения называют

исходные суждения, из которых выводится новое

суждение. Заключением называется новое

суждение, полученное логическим путем из

посылок. Логический переход от посылок к

заключению называется выводом.

Например: «Судья не может участвовать в

рассмотрении дела, если он является потерпевшим

(1). Судья Н. — потерпевший (2). Значит, судья Н.

не может участвовать в рассмотрении дела (3)».

В этом умозаключении 1-е и 2-е суждения

являются посылками, 3-е суждение —

Отношение логического следования между

посылками и заключением предполагает связь

между посылками по содержанию. Если суждения

не связаны по содержанию, то вывод из них

невозможен. Например, из суждений: «Судья не

может участвовать в рассмотрении дела, если он

является потерпевшим» и «Обвиняемый имеет

право на защиту» нельзя получить заключения, так

как эти суждения не имеют общего содержания и,

следовательно, логически не связаны друг с

другом.

При наличии содержательной связи между

посылками мы можем получить в процессе

рассуждения новое истинное знание при

соблюдении двух условий: во-первых, исходные

суждения — посылки умозаключения должны

быть истинными; во-вторых, в процессе

рассуждения следует соблюдать правила вывода,

которые обусловливают логическую правильность

умозаключения.

Умозаключения делятся на следующие виды.

1. В зависимости от строгости правил вывода

различают демонстративные (необходимые) и

недемонстративные (правдоподобные)

умозаключения. Демонстративные умозаключения

характеризуются тем, что заключение в них с

необходимостью следует из посылок, т.е.

логическое следование в такого рода выводах

представляет собой логический закон. В

недемонстративных умозаключениях правила

2. Важное значение имеет классификация

умозаключений по направленности логического

следования, т.е. по характеру связи между знанием

различной степени общности, выраженному в

посылках и заключении. С этой точки зрения

различают три вида умозаключений: дедуктивные

(от общего знания к частному), индуктивные (от

частного знания к общему), умозаключения по

аналогии (от частного знания к частному).

Эта классификация будет положена в основу

дальнейшего изложения.

Рассмотрим дедуктивные умозаключения.

Дедуктивными (от латинского deductio —

«выведение») называется умозаключение, в

котором переход от общего знания к частному

является логически необходимым. Правила

дедуктивного вывода определяются характером

посылок, которые могут быть простыми

(категорическими) или сложными суждениями. В

зависимости от количества посылок дедуктивные

выводы из категорических суждений делятся на

непосредственные, в которых заключение

выводится из одной посылки, и

опосредствованные, в которых заключение

выводится из двух посылок.

24. Простой категорический силлогизм и его

структура. Общие правила силлогизма.

Простой категорический силлогизм.

Простой категорический силлогизм состоит из

трех категорических суждений, два из которых

являются посылками, а третье — заключением.

Например,

«Обвиняемый имеет право на защиту.

Гусев — обвиняемый.

Гусев имеет право на защиту».

Расчленим суждения, из которых состоит

силлогизм, на понятия. Этих понятий три, причем

каждое из них входит в состав двух суждений.

«Обвиняемый» — в 1-е (посылку) как субъект и во

2-е (посылку) как предикат; <имеет право на

защиту» — в 1-е (посылку) и в 3-е (заключение)

как их предикаты; «Гусев» — во 2-е (посылку) и в

3-е (заключение) как их субъекты.

Понятия, входящие в состав • силлогизма,

называют терминами силлогизма. Различают

меньший, больший и средний термины.

Меньшим термином силлогизма называется

понятие, которое в заключении является

субъектом (в нашем примере понятие «Гусев»).

Большим термином силлогизма называется

понятие, которое в заключении является

предикатом («имеет право на защиту»). Меньший

и больший термины называются крайними и

обозначаются соответственно латинскими буквами

S (меньший термин) и Р (больший термин).

Каждый из крайних терминов входит не только

в заключение, но и в одну из посылок. Посылка, в

которую входит меньший термин, называется

меньшей посылкой, посылка, в которую входит

больший термин, называется большей посылкой. В

нашем примере большей посылкой будет первое

суждение (1), меньшей — второе суждение (2).

Средним термином силлогизма называется

понятие, входящее в обе посылки и

отсутствующее в заключении (в нашем примере —

«обвиняемый»). Средний термин обозначается

латинской буквой М.

Обвиняемый (М) имеет право на защиту (Р).

Гусев (S) — обвиняемый (М).

Гусев (S) имеет право на защиту (Р).

Итак, простой категорический силлогизм — это

умозаключение об отношении двух крайних

терминов на основании их отношения к среднему

термину.

Общие правила вывода в простом

категорическом силлогизме.

а) Правила терминов.

Из истинных посылок истинное заключение

можно получить только в том случае, если

соблюдаются правила силлогизма. Этих правил

семь: три относятся к терминам и четыре — к

посылкам.

1-е правило: в силлогизме должно быть только три

термина. Вывод в силлогизме основан на

отношении двух крайних терминов к среднему,

в нем не может быть ни меньше, ни больше

трех терминов. Нарушение этого правила связано

с отождествлением разных понятий, которые

принимаются за одно и рассматриваются как

средний термин. Эта ошибка основана на

нарушении требований закона тождества и

называется учетверением терминов. Нельзя,

например, получить заключение из посылок:

«Законы не создаются людьми» и «Закон — это

нормативный акт, принятый высшим органом

государственной власти», так как вместо трех

терминов мы имеем дело с четырьмя: в первой

посылке имеются в виду объективные законы,

существующие независимо от сознания людей, во

второй — юридический закон, устанавливаемый

государством. Это два разных понятия, которые не

могут связать крайние термины.

2-е правило: средний термин должен быть

распределен хотя бы в одной из посылок. Если

средний термин не распределен ни в одной из

посылок, то связь между крайними терминами

остается неопределенной. Например, в посылках

«Некоторые юристы (М) — члены коллегии

адвокатов (Р)», «Все сотрудники нашего

коллектива (S) — юристы (М)» средний термин

(М) не распределен в большей посылке, так как

является субъектом частного суждения, и не

распределен в меньшей посылке как предикат

утвердительного суждения. Следовательно,

средний термин не распределен ни

в одной из посылок. В этом случае

необходимую связь между крайними терминами (S

и Р) установить нельзя.

3-е правило: термин, не распределенный в

посылке, не может быть распределен и в

заключении. Например,

«Нравственные нормы (М) не санкционируются

государством (Р).

Нравственные нормы (М) — формы социальной

регуляции (S).

Некоторые формы социальной регуляции (S) не

санкционируются государством (Р).

Меньший термин (S) не распределен в посылке

(как предикат утвердительного суждения),

поэтому он не распределен и в заключении (как

субъект частного суждения). Делать вывод с

распределенным субъектом в форме общего

суждения («Ни одна форма социальной регуляции

не санкционируется государством») это правило

запрещает. Ошибка, связанная с нарушением

правила распределенности крайних терминов,

называется незаконным расширением меньшего

(или большего) термина.

б) Правила посылок.

1-е правило: хотя бы одна из посылок должна

быть утвердительным суждением. Из двух

отрицательных посылок заключение с

необходимостью не следует.

Например, из посылок «Студенты нашего

института (М) не изучают биологию (Р)»,

«Сотрудники НИИ (S) не являются студентами

нашего института (М)» нельзя получить

необходимого заключения, так как оба крайних

термина (S и Р) исключаются из среднего. По-

этому средний термин не может установить

определенного отношения между крайними

терминами.

2-е правило: если одна из посылок —

отрицательное суждение, то и заключение должно

быть отрицательным.

Например:

Судья, являющийся родственником

потерпевшего (М), не может участвовать в

рассмотрении дела (Р).

Судья К. (S) — родственник потерпевшего (М).

Судья К. (S) не может участвовать в

рассмотрении дела (Р).

3-е правило: хотя бы одна из посылок должна

быть общим суждением. Из двух частных посылок

заключение с необходимостью не следует.

Если обе посылки — частноутвердительные

суждения (II), то вывод сделать нельзя согласно 2-

му правилу терминов: в частноутвердительном

суждении ни субъект, ни предикат не распределе-

ны, поэтому и средний термин не распределен ни в

одной из посылок.

Если обе посылки — частноотрицательные

суждения (00), то вывод сделать нельзя согласно

1-му правилу посылок.

Если одна посылка — частноутвердительная, а

другая — частнотрицательная (Ю или 01), то в

таком силлогизме распределенным будет только

один термин — предикат частноотрицательного

суждения. Если этим термином будет средний, то

вывода сделать нельзя, так как согласно 2-му

правилу посылок заключение должно быть

отрицательным. Но в этом случае предикат

заключения должен быть распределен, что

противоречит 3-му правилу терминов: 1) больший

термин, не распределенный в посылке, окажется

распределенным в заключении; 2) если же

больший термин распределен, то вывода не

следует согласно 2-му правилу терминов.

4-е правило: если одна из посылок — частное

суждение, то и заключение должно быть частным.

Если одна посылка общеутвердительная, а

другая — частноутвердительная (Al, IA), то в них

распределен только один термин — субъект

общеутвердительного суждения.

Согласно 2-му правилу терминов, это должен

быть средний термин. Но в таком случае два

крайних термина, в том числе меньший, не будут

распределены. Поэтому в соответствии с 3-м пра-

вилом терминов меньший термин не будет

распределен в заключении, которое будет частным

суждением.

Если одна из посылок утвердительная, а другая

— отрицательная, причем одна из них частная (EI,

АО, ОА), то распределенными окажутся два

термина: субъект и предикат общеотрицательного

суждения (EI) или субъект общего и предикат

частного суждения (АО, ОА). Но в том и другом

случае, согласно 2-му правилу посылок,

заключение будет отрицательным, т.е. суждением

с распределенным предикатом. А так как вторым

распределенным термином должен быть средний

(2-е правило терминов), то меньший термин в

итоге окажется нераспределенным, т.е.

заключение будет частным.

25. Фигуры силлогизма и их правила.

Фигуры простого категорического силлогизма.

Модусы простого категорического силлогизма.

а) Первая фигура

В посылках простого категорического

силлогизма средний термин может занимать место

субъекта или предиката. В зависимости от этого

различают четыре разновидности силлогизма

которые называют фигурами. Фигуры силлогизма

— это его разновидности, различающиеся

положением среднего термина в посылках.

В первой фигуре средний термин занимает

место субъекта в большей и место предиката в

меньшей посылках.

Посылками силлогизма могут

быть суждения, различные по

качеству и количеству:

общеутвердительные (А), общеотрицательные (Е),

частноутвердительные (I) и частноотрицательные

(О).

Разновидности силлогизма, различающиеся

количественными и качественными

характеристиками посылок, называются модусами

простого категорического силлогизма. Общее

количество вариантов в четырех фигурах 64

модуса, но правильными, т.е. соответствующими

всем правилам, являются только 19 из них. По

первой фигуре это модусы: ААА, ЕАЕ, АН, ЕЮ.

Помимо общих правил существуют

специальные правила фигур.

Правила 1 -й фигуры:

1. Большая посылка — общее суждение.

2. Меньшая посылка — утвердительное

суждение.

Первая фигура — наиболее типичная форма

дедуктивного умозаключения. Из общего

положения, выражающего нередко закон науки,

правовую норму, делается вывод об отдельном

факте, единичном случае, конкретном лице.

Широко применяется эта фигура в судебной

практике. Юридическая оценка (квалификация)

правовых явлений, применение нормы права к

отдельному случаю, назначение наказания за

преступление, совершенное конкретным лицом, и

другие судебные решения принимают логическую

форму 1-й фигуры силлогизма.

б) Вторая фигура.

Во второй фигуре — место предиката в обеих

посылках.

Разновидности силлогизма, различающиеся

количественными и качественными

характеристиками посылок, называются модусами

простого категорического силлогизма.

Общее количество вариантов в четырех

фигурах 64 модуса, но г правильными, т.е.

соответствующими всем правилам, являются г

только 19 из них по второй фигуре: ЕАЕ, АЕЕ,

ЕЮ, АОО.

Помимо общих правил существуют

специальные правила фигур.

Правила 2-й фигуры: г 1. Большая посылка —

общее суждение. Ь 2. Одна из посылок —

отрицательное суждение.

2-я фигура применяется, когда необходимо

показать, что I отдельный случай (конкретное

лицо, факт, явление) не может быть I подведен под

общее положение. Этот случай исключается из

числа предметов, о которых сказано в большей

посылке. В судебной I практике 2-я фигура

используется для заключений об отсутствии I

состава преступления в данном конкретном

случае, для опровержения положений,

противоречащих тому, о чем говорится в посылке,

выражающей общее положение.

в) Третья фигура.

В третьей фигуре — место субъекта в обеих

посылках.

Посылками силлогизма могут быть суждения,

различные по •качеству и количеству:

общеугвердительные (А), общеотрицательные (Е),

частноутвердительные (I) и частноотрицательные

(О).

Разновидности силлогизма,

различающиеся количе-

ственными и качественными

характеристиками посылок, на-

зываются модусами простого категорического

силлогизма.

Общее количество вариантов в четырех

фигурах 64 модуса, но правильными, т.е.

соответсвующими всем правилам, являются

только 19, из них по третьей фигуре: AAI, IAI, All,

EAO, ОАО, ЕЮ.

Помимо общих правил существуют

специальные правила фигур.

Правила 3-й фигуры:

1. Меньшая посылка — утвердительное

суждение.

2. Заключение — частное суждение.

Давая только частные заключения, 3-я фигура

применяется чаще всего для установления

частичной совместимости признаков, относящихся

к одному предмету. В практике рассуждения 3-я

фигура применяется сравнительно редко.

26. Разделительное умозаключение и его

разновидности.

Разделительным называется умозаключение,

одна из посылок которого является

разделительным суждением, а другая посылка и

вывод являются категорическими суждениями.

Разделительное умозаключение является

правильным при определенных условиях, а

именно: части разделительного умозаключения в

посылке находятся в отношении исключающего

разделения (строгой дизъюнкции);

части разделительного суждения в посылке

исчерпывают объем делимого понятия.

Разделительное умозаключение существует в

двух модусах: modus ponendo tolens —

положительно-отрицательный, modus tollendo

ponens — отрицательно-положительный.

Modus ponendo tolens представляет собой

умозаключение, большая посылка которого

является разделительным суждением, меньшая —

утвердительным суждением, а вывод —

отрицательным суждением.

Каждое А есть либо В, либо С;

А есть В;

Следовательно, А не есть С.

Например:

Все разумные тварные существа суть либо ангелы,

либо люди;

Данное существо есть человек;

Следовательно, оно не есть ангел.

Как было отмечено выше, разделительное

суждение должно быть исключающим, а объем

членов суждения должен совпадать с объемом

делимого понятия.

Студент N не сдал экзамен либо по болезни, либо

по нерадению, либо в силу отсутствия на занятиях;

Студент N отсутствовал на занятиях.

Вывод сделать нельзя, поскольку и то, и другое,

и третье могло оказаться причиной недостаточной

подготовки студента N; кроме того, студент мог не

сдать экзамен и по иной причине, которая не

указана в разделительном суждении.

Modus tollendo ponens представляет собой

умозаключение, большая посылка которого

является разделительным суждением, меньшая —

отрицательным суждением, а вывод —

положительным суждением.

Каждое А есть либо В, либо С;

Данное А не есть В;

Следовательно, данное А есть С.

Например:

Все сущее есть или тварное, или нетварное;

Человек не есть нетварное существо;

Следовательно, человек есть тварное существо.

33. Общая характеристика законов

логики как законов правильного

мышления.

Формально-логические законы

складывались и развивались по мере

развития разума. Эти законы -

своеобразная фиксация свойств и

признаков, постоянно наблюдаемых в

реальной жизни: таких как определенность,

уникальность и стабильность объектов

окружающего мира. Но здесь должно быть

четкое понимание: логические законы - это

не фиксация конкретных законов развития

мира. Будучи аналитическими

предложениями, они не могут ничего

сказать о фактическом мире. Это именно

законы правильного построения

мыслительных цепочек. В этом смысле -

как выразители признаков правильного

мышления - они действуют в абсолютно

любом рассуждении, к чему-бы оно ни

применялось. Таким образом - логические

законы относятся только к форме

мышления, а не к его объекту.

Поэтому формально-логические законы

абсолютно глобальны в социально-

культуральном смысле - они действуют во

все времена и во всех странах, люди

разных национальностей и разной

культуры мыслят логически, используя

одни и те-же законы.

Собственно - вот эти законы:

1. Закон тождества

2. Закон непротиворечия

3. Закон исключенного третьего

4. Закон достаточного основания

Исходя из самого названия, правильное

мышление должно удовлетворять

некоторым обязательным правилам,

подчиняться некоторым законам, не

зависящим от конкретных точек его

приложения. И подобными правилами

выступают законы формальной логики.

27. Условное умозаключение и его

разновидности.

Общая характеристика дедуктивных

умозаключений и его виды

В процессе познания действительности мы

приобретаем новые знания. Некоторые из них

непосредственно, в результате воздействия

предметов внешнего мира на органы чувств; но

большую часть знаний мы получаем путем

выведения новых знаний из знаний уже

имеющихся. Эти знания называются

опосредованными, или выводами.

Логической формой получения выводных

знаний являются умозаключение.

Умозаключение - это форма мышления,

посредством которой из одного или нескольких

суждений выводиться новое суждение. Любое

умозаключение состоит из посылок, заключения и

вывода. Посылками умозаключения называются

исходные суждения, из которых выводится новое

суждение. Заключением называется новое

суждение, полученное логическим путем из

посылок. Логический переход от посылок к

заключению называется выводом.

Например: "Следователь не может участвовать в

расследовании дела, если он является

потерпевшим (1). Следователь П. - потерпевший

(2). Значит, он не может участвовать в

расследовании дела (3)".

В этом умозаключении 1-е и 2-е суждение

являются посылками, 3-е суждение - заключением.

Отношение логического следования между

посылками и заключением предполагает связь

между посылками по содержанию. Если суждения

не связаны по содержанию, то вывод из них

невозможен. Например, из суждений:

"Следователь не может участвовать в

расследовании дела, если он является

потерпевшим" и "Обвиняемый имеет право на

защиту" - нельзя получить заключения, так как эти

суждения не имеют общего содержания и,

следовательно, логически не связаны друг с

другом.

При наличии содержательной связи между

посылками мы можем получить в процессе

рассуждения новое истинное знание при

соблюдении двух условиях: во-первых, должны

быть истинными исходные суждения - посылки

умозаключения; во-вторых, в процессе

рассуждения следует соблюдать правила вывода,

которые обуславливают логическую правильность

умозаключения.

В зависимости от строгости правил вывода

различают два вида умозаключений:

демонстративное (необходимые) и

недемонстративное (правдоподобные).

Демонстративные умозаключения

характеризуются тем, что заключение в них с

необходимостью следует из посылок, т.е.

умозаключениях правила вывода обеспечивают

лишь вероятное следование заключение из

посылок.

Наряду с делением умозаключений по

строгости вывода важное значение имеет их

классификация по направленности логического

следования, т.е. по характеру связи между знанием

различной степени общности, выраженному в

посылках и значении. С этой точки зрения

различают три вида умозаключений: дедуктивные

(от общего знания к частному), индуктивные (от

частного к общему), умозаключения по аналогии

(от частного к частному).

Дедуктивные умозаключения - те умозаключения,

у которых между посылками и заключениями

имеется отношение логического следования.

Например: "Все рыбы дышат жабрами (1). Все

окуни - рыбы (2). Значит все окуни дышат

жабрами (3)."

Здесь первая посылка "Все рыбы дышат жабрами"

является общеутвердительным суждением и

выражает большую степень обобщения по

сравнению с заключением, также являющимся

общеутвердительным суждением "Все окуни

дышат жабрами". Мы строим умозаключения от

признака, принадлежащего роду ("рыба"), к его

принадлежности к виду - "окунь", т.е. от общего

класса к его частному случаю, к подклассу.

29. Научная индукция, требования,

предъявляемые к ней.

Индукция. Познание в любой области науки и

практики начинается с эмпирического познания. В

процессе наблюдения однотипных природных и

социальных явлений фиксируется внимание на

повторяемости у них определенных признаков.

Устойчивая повторяемость наводит на мысль

(индуцирует), что каждый из таких признаков

является не индивидуальным, а общим, присущим

всем явлениям определенного класса. Логический

переход от знания об отдельных явлениях к

знанию общему совершается в этом случае в

форме индуктивного умозаключения, или

индукции (от латинского inductio — «наведение»).

Индуктивным называется умозаключение, в

котором на основании принадлежности признака

отдельным предметам или частям некоторого

класса делают вывод о его принадлежности классу

в целом.

В основе логического перехода от посылок к

заключению в индуктивном выводе лежит

подтверждаемое тысячелетней практикой

положение о закономерном развитии мира,

всеобщем характере причинной связи, проявлении

необходимых признаков явлений через их

всеобщность и устойчивую повторяемость.

Именно эти методологические положения

оправдывают логическую состоятельность и

эффективность индуктивных выводов.

Основная функция индуктивных выводов в

процессе познания — генерализация, т.е.

получение общих суждений. По своему

содержанию и познавательному значению эти

обобщения могут носить различный характер — от

простейших обобщений повседневной практики до

эмпирических обобщений в науке или

универсальных суждений, выражающих всеобщие

законы.

Популярная и научная индукция

В процессе многовековой деятельности люди

наблюдают устойчивую повторяемость многих

явлений. На этой основе возникают обобщения,

которые используются для объяснения

наступивших и предсказания будущих событий и

явлений. Такого рода обобщения бывают связаны

с наблюдениями над погодой, влиянием

климатических условий на урожай, причинами

распространения болезней, поведением людей в

определенных ситуациях, отношениями между

людьми и т.п. Логический механизм большинства

таких обобщений — популярная индукция. Ее

иногда называют индукцией через простое

перечисление.

Повторяемость признаков во многих случаях

действительно отражает всеобщие свойства

явлений. Построенные на ее основе обобщения

выполняют важную функцию направляющих

начал в практической деятельности людей. Без

таких простейших обобщений невозможен ни

совершенствование орудий труда, развитие

мореплавания, успешное ведение земледелия,

контакты между людьми в социальной среде.

В процессе расследования преступлений часто

используют эмпирические индуктивные

обобщения, касающиеся поведения лиц,

причастных к преступлению. Например: лица,

совершившие преступления, стремятся скрыться

от суда и следствия; угроза убийством часто

приводится в исполнение; обнаружение

похищенных вещей (поличное) свидетельствует о

причастности к преступлению. Такие опытные

обобщения, или фактические презумпции, как их

нередко называют в юридической литературе,

часто оказывают неоценимую помощь следствию

несмотря на то, что они являются

проблематичными суждениями. Популярная

индукция определяет первые шаги и в развитии

научных знаний.

Некорректно построенные индуктивные

обобщения нередко лежат в основе различного

рода суеверий, невежественных поверий и примет

вроде «дурного глаза», «хороших» и «дурных»

сновидений, перебежавшей дорогу черной кошки

и т.п.

Научной индукцией называют умозаключение,

в котором обобщение строится путем отбора

необходимых и исключения случайных

обстоятельств.

В зависимости от способов исследования

различают: (1) индукцию методом отбора

(селекции) и (2) индукцию методом исключения

(элиминации).

Индукция методом отбора, или селективная

индукция, — это умозаключение, в котором вывод

о принадлежности признака классу (множеству)

основывается на знании об образце

(подмножестве), полученном методичным отбором

явлений из различных частей этого класса.

Индукция методом исключения, или

элиминативная индукция, — это система

умозаключений, в которой выводы о причинах

исследуемых явлений строятся путем

обнаружения подтверждающих обстоятельств и

исключения обстоятельств, не удовлетворяющих

свойствам причинной связи.

Познавательная роль элиминативной индукции

— анализ причинных связей. Причинной

называют такую связь между двумя явлениями,

когда одно из них — причина — предшествует и

вызывает другое — действие, Важнейшими

свойствами причинной связи,

предопределяющими методичность

элиминативной индукции, выступают такие ее

характеристики, как: (1) всеобщность, (2)

последовательность во времени, (3)

необходимость и (4) однозначность.

30. Индуктивные методы установления

причинно-следственных связей.

Логический переход от знания об отдельных

явлениях к знанию общему совершается в

форме индуктивного умозаключения, или

индукции (от лат. — наведение).

Индуктивным называется умозаключение, в

котором на основании принадлежности

признака отдельным предметам или частям

некоторого класса делают вывод о его принад-

лежности классу в целом.

В истории физики, например, опытным

путем было установлено, что железные

стержни хорошо проводят электричество.

Такое же свойство было обнаружено у медных

стержней и серебра. Учитывая

принадлежность указанных проводников к

металлам, было сделано индуктивное

обобщение, что всем металлам свойственна

электропроводность.

Посылками индуктивного умозаключения

выступают суждения, в которых фиксируется

полученная опытным путем информация о

повторяемости признака Р у ряда явлений —

S1, S2, .... Sn, принадлежащих одному и тому

же классу К.

Схема умозаключения имеет следующий

вид:

1) S1 имеет признак Р;S2 имеет признак Р;

Sn имеет признак Р.

2) S1, S2,.., Sn- элементы (части) класса К.

Всем предметам класса К присущ признак Р.

В основе логического перехода от посылок

к заключению в индуктивном выводе лежит

подтверждаемое тысячелетней практикой

положение о закономерном развитии мира,

всеобщем характере причинной связи,

проявлении необходимых признаков явлений

через их всеобщность и устойчивую

повторяемость. Именно эти методологические

положения оправдывают логическую

состоятельность и эффективность

индуктивных выводов.

Основная функция индуктивных выводов в

процессе познания — генерализация, т.е.

получение общих суждений. По своему

содержанию и познавательному значению эти

обобщения могут носить различный характер

— от простейших обобщений повседневной

практики до эмпирических обобщений в науке

или универсальных суждений, выражающих

всеобщие законы.

Важное место принадлежит индуктивным

выводам в судебно-следственной практике —

на их основе формулируются многочисленные

обобщения, касающиеся обычных отношений

между людьми, мотивов и целей совершения

противоправных действий, способов

совершения преступлений, типичных реакций

виновников преступления на действия

следственных органов и т.п.

В зависимости от полноты и законченности

эмпирического исследования различают два

вида индуктивных умозаключений: полную

индукцию и неполную. В неполной индукции

различают популярную и научную в

зависимости от способа отбора исходного

материала. Научная индукция делится в

зависимости от способа исследования на

индукцию методом отбора и индукцию

методом исключения.

31. Аналогия, общая характеристика и

особенности аналогии как формы

умозаключения.

Аналогия (подобие, сходство)- имеют в виду

рассуждения, состоящие в том, что на основе

сходства двух предметов (систем предметов) а и b

по каким-то характеристикам, а так же на основе

того, что а присущ некоторый признак, заключают

о присущности b того же признака.

Различаются по наличию одного и отсутствием

другого признака. Это вытекает из принципа

тождества неразличимого Лейбница, согласно

которому два предмета тождественны (т.е.

являются одним и тем же предметом) тогда и

только тогда, когда все свойства, которыми они

обладают-одинаковы).

Различают научную и популярную аналогию.

Популярная аналогия строится без какого-либо

систематического анализа и отбора свойств, по

которым устанавливают наличие подобия. 1.нужно

обнаружить как можно больше признаков,

2.признаки должны быть существенными

3.признаки должны принадлежать только

сравниваемым предметам 4.признаки должны

быть разнородными 5.общие признаки должны

быть тесно связаны с переносимым признаком.

Научная аналогия двух видов: 1.используется

теория, объясняющая связь признаков и

переносимого признака, на ней базируется метод

моделирования-изучения объектов при помощи

Модель-объект, сходный с другим объектом-

оригиналом. 2. 1.общие признаки должны быть в

точности одинаковы, 2.связь общих признаков и

переносимого признака не должна зависить от

специфики предметов.

Ф-ии аналогии: 1.эвристическая- позволяет

открыть новые факты. 2.объясняющая- служит

средством объяснения явлений. 3.доказательная-

аргументация в качестве доказательства.

4.гнесеологическая-аналогия выступает в качестве

средства познания.

Аналогия

В науке и практических делах объектом

исследования нередко выступают единичные,

неповторимые по своим индивидуальным

характеристикам события, предметы и явления.

При их объяснении и оценке затруднено

применение как дедуктивных, так и индуктивных

рассуждений. В этом случае прибегают к третьему

способу рассуждения— умозаключению по

аналогии: уподобляют новое единичное явление

другому, известному и сходному с ним

единичному явлению и распространяют на первое

ранее полученную информацию.

Например, историк или политик, анализируя

революционные события в конкретной стране,

уподобляет их ранее совершенной в другой стране

сходной революции и на этой основе прогнозирует

развитие политических событий.

Умозаключению по аналогии всегда

предшествует операция сравнения двух объектов,

которая позволяет установить сходства и различия

между ними. При этом для аналогии требуются не

любые совпадения, а сходства в существенных

признаках при несущественности различий.

Именно такие сходства служат основой для

уподобления двух материальных или идеальных

объектов

Аналогия не является произвольным

логическим построением, в ее основе лежат

объективные свойства и отношения предметов

реальной действительности. Каждый конкретный

предмет, обладая множеством признаков,

представляет не случайную их комбинацию, а

определенное единство. Каким бы малочисленным

ни был тот или иной признак, его существование и

изменение всегда обусловлено состоянием других

сторон предмета или внешних условий.

32. Виды умозаключения по аналогии.

Оперирование умозаключениями по аналогии

занимает значительное место в теоретической и

практической деятельности человека. Важное

значение в этой связи приобретает знание видовой

характеристики аналогии и умение ее

использовать как в конкретном мыслительном

процессе, так и в специфической

профессиональной деятельности личности,

особенно в экономической, юридической,

филологической.

Виды аналогий, исходя из конкретных

критериев (оснований), можно классифицировать

на две устойчивые группы.

1 - ая группа. Исходя из характера предмета

анализа, она может быть представлена в виде: 1)

аналогии свойств и качеств предметов; 2) аналогии

отношений предметов.

В первом случае рассматриваются два единичных

предмета (или же два множества однородных

предметов, т.е. два класса), а переносимыми

признаками выступают свойства этих предметов.

Примером аналогии свойств может являться

аналогия симптомов протекания какой-либо

болезни (например, гриппа) у разных людей или у

двух групп людей (например, инженеры и

учителя). Исходя из сходства признаков болезни,

врач ставит определенный диагноз.

Общая схема аналогии свойств в формальной

логике следующая:

Предмет х обладает свойствами а , b , с , d , е , f

Предмет у обладает свойствами а, b, с, d

Вероятно, предмет у обладает свойствами e , f

Второй вид - аналогия отношений предметов -

имеет свою особенность по сравнению с аналогией

свойств и качеств предметов. Аналогия отношений

представляет собой такое умозаключение, в

котором уподобляются друг другу два отношения

между предметами, а не их сами и их свойства.

Примером в данном случае служит планетарная

модель строения атома, предложенная Э.

Резерфордом. Известный ученый построил ее на

основании аналогии отношения между Солнцем и

планетами, с одной стороны, и отношения между

ядром атома и электронами, которые

удерживаются на своих орбитах в силу

притяжения ядром, - с другой стороны.

2 - ая группа. Исходя из степени достоверности

ожидаемого вывода, аналогия подразделяется на

виды: 1) строгая аналогия; 2) нестрогая аналогия.

Специфическим признаком, отличающим строгую

аналогию, является наличие необходимой связи

общих признаков с переносимым признаком.

Схема строгой аналогии такова:

Предмет X обладает признаками а , b , с , d , e

Предмет У обладает признаками а, b, с, d

Из совокупности признаков а, e, с, d необходимо

следует Предмет У обязательно обладает

признаком е.

Строгая аналогия находит применение в

научных исследованиях, а также в математических

доказательствах. Так, формулирование признаков

подобия двух треугольников основано на строгой

аналогии. Напомним: "Если три угла одного

треугольника равны трем углам другого

треугольника, то такие треугольники подобны"

Правила аналогии

Для успешного применения аналогии важно

соблюдать определенные логические правила,

выполнение которых в немалой степени повышает

вероятность вывода, а в определенных

обстоятельствах придает ему вполне

обоснованный характер.

Правило первое. При сопоставлении

сравниваемых предметов (явлений) необходимо

всесторонне изучать их сходство и различие в

существенных признаках. Иными словами,

сравниваемые предметы (явления) должны быть

связаны между собой по существу, а не

формально.

Правило второе. В процессе аналогии

необходимо установить у предметов (явлений) как

можно больше разнообразных сходных признаков,

связанных с переносимым свойством. Чем больше

сходных признаков и разнообразнее их отношения

к переносимому свойству, тем скорее достигается

значительная полнота условий для вывода по

аналогии.

Правило третье. В процессе сопоставления

предметов (явлений) следует выявить

необходимую связь общих признаков с

переносимым свойством, т.е. показать, что

сходные признаки в своей совокупности

обеспечивают присутствие переносимого свойства

у предмета (явления) изучения.

Кроме того, аналогия может быть применена и

в юридической практике, особенно в ходе

расследования. Сравнение конкретного уголовного

дела с уже исследованными явлениями

способствует выявлению сходства между ними.

Благодаря этому (осуществив подобие) можно

обнаружить ранее не известные признаки и

обстоятельства преступления.

Таким образом, соблюдение правил

умозаключения по аналогии (а их в литературе

также еще называют условиями) способствует

повышению вероятности достижения истины в

различных отраслях деятельности человека.

34. Закон тождества.

Первый закон - закон тождества – позволяет

сознательно отделить правильные рассуждения от

неправильных и найти логическую ошибку в

рассуждении.

Формулировка: всякое понятие и суждение

тождественно самому себе.

Внешне самым простым из логических законов

является закон тождества. Он говорит: если

высказывание истинно, то оно истинно. Иначе

говоря, каждое высказывание вытекает из самого

себя и является необходимым и достаточным

условием своей истинности. Символически:

АА, если А, то А. Например: «Если дом

высокий, то он высокий», «Если трава черная, то

она черная» и т.п.

В приложениях закона тождества к

конкретному материалу с особой наглядностью

обнаруживается отмечавшаяся ранее общая черта

всех логических законов. Они представляют собой

т а в т о л о г и и, как бы повторения одного и того

же и не несут содержательной, «предметной»

информации. Это - общие схемы, отличительная

особенность которых в том, что подставляя в них

любые конкретные высказывания (как истинные,

так и ложные), мы обязательно получим истинное

выражение.

Закон тождества нередко ошибочно подменяется т

р е б о в а н и е м у с т о й ч и в о с т и

, о п р е д е л е н н о с т и мышления.

Действительно, в процессе рассуждения значения

понятий и утверждений не следует изменять. Они

должны оставаться тождественными самим себе,

иначе свойства одного объекта незаметно

окажутся приписанными совершенно другому.

Если мы начали говорить, допустим, о спутниках

как небесных телах, то слово «спутник» должно,

пока мы обсуждаем эту тему, обозначать именно

такие тела, а не каких-то иных спутников.

Требование не изменять и не подменять значения

слов в ходе рассуждения, конечно, справедливо.

Но, очевидно, что оно не является законом логики.

Точно так же, как не относится к ним совет

выделять обсуждаемые объекты по достаточно

устойчивым признакам, чтобы уменьшить

вероятность подмены в рассуждении одного

объекта другим.

Иногда закон тождества неверно

истолковывается как один из законов бытия,

говорящий о его относительной устойчивости и

определенности. Понятый так, он превращается в

утверждение, что вещи всегда остаются

неизменными, тождественными самим себе. Такое

понимание этого закона, конечно, ошибочно.

Закон ничего не говорит об изменчивости или

неизменности. Он утверждает только, что если

вещь меняется, то она меняется, а если она

остается той же, то она такой же и остается.

35. Закон противоречия.

Второй закон - закон непротиворечия –

определяет истинность умозаключения, т.к.два

противоположных суждения об одном и том же

предмете не могут быть истинны в одно и то же

время в одном и том же отношении.

Комментарий: я начну его с известного всем

парадокса об абсолютной броне и абсолютном

снаряде:

Может ли снаряд, пробивающий абсолютно все,

пробить броню, которая абсолютно ничем не

пробиваема?

Для ответа на этот парадокс достаточно еще раз

взглянуть на формулировку второго закона, чтобы

получить правильное решение:

При заданных условиях задача логически

противоречива: всепробивающий снаряд и

неразрушимая броня не могут существовать

одновременно.

Если первый закон выражает отношение

логической однозначности, то второй - отношение

логической несовместимости. Он действует в

отношении любых противоположных суждений - и

противных (контрарных) и противоречащих

(контрадикторных). Итак - оба противоположных

суждения не могут быть одновременно

истинными, по крайне мере одно из них

необходимо ложно. О том, каким может быть

второе утверждение, закон непротиворечия не

говорит.

В основе закона непротиворечия лежит

качественная определенность вещей и явлений,

относительная устойчивость их свойств. Но нужно

четко понимать, что второй закон отрицает только

логические противоречия. Это отрицание не имеет

никакого отношения к противоречиям реальной

действительности. Формально-логические

противоречия - это не противоречия объективной

действительности, а противоречия неправильного

рассуждения.

Интересно, что постоянно предпринимаются

попытки оспорить закон непротиворечия -

буквально со времен Аристотеля, впервые его

сформулировавшего. Основная часть подобных

попыток связана с неверным толкованием понятия

"логическое отрицание". Логическое отрицание

имеет место тогда, и только тогда, когда

высказывание и его отрицание совпадают

абсолютно во всем (т.е. относятся к одному и тому

же объекту, рассматриваемому в одном и том же

отношении), кроме одной единственной вещи: то,

что утверждается в одном высказывании,

отрицается в другом. Если это простое правило не

соблюдается - противоречия фактически нет,

поскольку нет отрицания.

Пример: На вопрос, хочу ли я есть, я отвечаю: "И

да и нет". Противоречие, вроде-бы, налицо, ведь

формально-логически невозможно в одно и то-же

время одновременно и хотеть и не хотеть

одного и того-же. На самом деле такой ответ

может быть вполне осмысленным, и приниматься

за противоречивый только ввиду его

лаконичности. Если попросить меня объяснить

(развернуть) свой ответ, я скажу : "Если

приготовлен шашлык, я , пожалуй, поем, в

остальных случаях - воздержусь". Противоречие

исчезает сразу, как только выясняется, что

утверждение относится к одному объекту

(шашлык), а отрицание - к другому (вся остальная

еда). Таким образом, в основе подобных

противоречий - не нарушение второго закона

логики, а риторика и метафоричность, цель

которых - кажущаяся парадоксальность

высказывания. Эта цель чаще всего достигается

путем банального несоблюдения первого закона -

закона тождества (объекта, времени или

отношения): "Я и спал, и не спал", "Ни жив ни

мертв", "Песня слышится, и не слышится",

"Умный, но дурак" и пр. Подобные (логически-

мнимые) противоречия широко применяются в

художественной литературе и в бытовых диалогах,

но они не несут логической нагрузки.

Литературные цели применения подобных

оборотов неисчерпаемы: усиление

выразительности, ироничности, скрытая насмешка

или подсказка и пр. "Он был чертовски умен -

даже знал таблицу умножения на шесть", "Да она

просто немая - говорить не более ста слов в

минуту" - я думаю, комментарии излишни.

Если принять, что истинно такое высказывание,

которое соответствует действительности, а ложное

- то, что ей не соответствует, то закон

непротиворечия можно будет сформулировать так:

"Ни одно высказывание не является одновременно

и истинным и ложным". В такой формулировке

закон особенно убедителен, т.к. истина и ложь -

две несовместимые характеристики высказывания.

Истинное высказывание соответствует

действительности, ложное не соответствует ей.

Тот, кто отрицает закон противоречия, должен

признать, что в этом случае одно и то же

высказывание может соответствовать реальному

положению вещей и одновременно не

соответствовать ему. В таком случае сами понятия

истины и ложности становятся бессмысленными, в

том числе - и как критерии оценки знания.

Вывод: Утверждая что-либо о каком-либо

объекте, мы не можем, не противореча себе,

отрицать то же самое о том же самом объекте,

взятом в то же самое время и в том же самом

отношении.

Результат применения: второй закон

обеспечивает непротиворечивость и

последовательность мышления, способность

фиксировать и исправлять всякого рода

противоречия в своих и чужих рассуждениях.

36. Закон исключенного третьего.

Третий закон - закон исключенного третьего

Формулировка: два противоречащих суждения

не могут быть одновременно ложными: одно из

них необходимо истинно; другое - необходимо

ложно; третье суждение исключено.

Или - более краткий вариант: "Из двух

противоречащих друг другу суждений одно

истинно, другое ложно, а третьего не дано".

Истинность отрицания равнозначна ложности

утверждения. В силу этого закон исключенного

третьего можно передать и так: "Каждое

высказывание является или истинным или

ложным".

Комментарий: Само название закона выражает

его смысл: дело может обстоять только так, как

описывается в рассматриваемом высказывании,

или так, как говорит его отрицание, и никакой

третьей возможности нет. Если закон

непротиворечия утверждает, что из двух

противоположных высказываний одно -

необходимо ложно, то закон исключения третьего

говорит, что одно из них - обязательно истинно. А

так как одно и то-же высказывание не может быть

одновременно и истинным и ложным, то имеем то,

что одно из этих высказываний обязательно

истинно, другое - ложно, а какому-нибудь

третьему варианту просто не остается места.

Поскольку закон исключенного третьего действует

только в отношении противоречащих

суждений, из которых одно необходимо

истинно, а другое необходимо ложно, то

рассуждение ведется по формуле: "ИЛИ-ИЛИ"

("Или пришел, или НЕ пришел", "Или живой или

НЕ живой", "Или черный, или НЕ черный" и пр).

Таким образом - даже еще не ознакомившись с

каким-то утверждением (например - гипотезой),

мы зарание планируем только два вида развития

событий - эта гипотеза может оказаться либо

истинной, либо ложной. Других вариантов просто

нет. Существует масса ироничных обыгрываний

этого закона - ведь сказать о чем-то, что оно "либо

есть, либо нет" - фактически не сказать ничего.

Помните анкдот о том, что "могу копать, а могу и

не копать"? Но вся эта ирония уместна лишь в том

случае, если закон применяется на неверном поле -

когда при помощи него пытаются или найти

истину, или сформулировать заключение о

реальном мире. Но закон исключенного третьего и

не призван указывать, какое именно из данных

суждений истинно. Этот вопрос решается при

помощи практики, устанавливающей соответствие

или несоответствие суждения объективной

действительности. Однако этот закон задает

направление нашего мышления в поиске истины -

возможно только два решения вопроса, причем

одно из них необходимо является истинным.

Всякое третье, среднее решение исключено.

Критика закона исключенного третьего

(Л.Бауэр) привела к созданию нового направления

в логике - интуиционистской логики. В последней

не принимается этот закон и отбрасываются все те

способы рассуждения, которые с ним связаны.

Среди отброшенных, например, оказывается

доказательство путем приведения к противоречию,

или абсурду.

Обращаю внимание на суть любой критики

законов формальной логики: все сторонники

концепции "расширения" формальной логики

сдвигают центр тяжести логических исследований

с изучения правильных способов рассуждения на

разработку каких-либо конкретных проблем:

теории познания, причинности, индукции и т.д. В

логику вводятся темы, интересные и важные сами

по себе, но не имеющие отношения к собственно

формальной логике, как к набору приемов

правильного мышления.

Закон исключенного третьего, не рассматривая

самих противоречий, запрещает признавать

одновременно истинным или одновременно

ложным два противоречащих друг другу

суждения. В этом и состоит его смысл.

Вывод: нельзя уклоняться от признания

истинным одного из двух противоречащих друг

другу высказывай и искать нечто третье между

ними.

Результат применения: достигается

однозначность логического мышления.

С законом исключенного третьего косвенно

связан следующий методологический принцип:

анализ каждого объекта должен вестись до тех пор

и быть настолько полным, чтобы относительно

любого утверждения об этом объекте можно было

решить, истинно оно или нет. Это требование

полноты и всесторонности исследования не

относится, конечно, к законам логики. Оно

полезно, но нередко оказывается невыполнимым.

В случае рассуждении о бесконечных и

неопределенных совокупностях объектов, об

изменяющихся, текущих состояниях и т.п.

изучение объекта не всегда способно достичь

такой полноты, чтобы на любой вопрос о нем

удалось ответить однозначно «да» или «нет».

37. Закона достаточного основания.

Четвертый закон - закон достаточного

основания

Формулировка: всякая истинная мысль имеет

достаточное основание.

Комментарий: Этот закон фактически заявляет

то, что все мысли которые можно объяснить,

считаются истинными, а те которые объяснить

нельзя - ложными. В логике высказываний этот

закон формулы не имеет, так как он имеет

содержательный характер. На этом стоит

остановиться несколько подробней:

Достаточным, т. е. действительным,

невымышленным основанием наших мыслей

может являться индивидуальная практика.

Действительно, истинность некоторых суждений

подтверждается путем их непосредственного

сопоставления с фактами действительности

(Пример: "[Истинно, что]Идет дождь", "[Является

ложью то, что]Я был в Акапулько"). Но личный

опыт ограничен. Поэтому в реальной деятельности

всегда приходится опираться на опыт других

людей. Благодаря развитию научных знаний

субъект использует в качестве оснований своих

мыслей опыт предшественников, закрепленный в

законах и аксиомах науки, в принципах и

положениях, существующих в любой области

человеческой деятельности. Для подтверждения

какого-либо частного случая нет необходимости

обращаться к его практической

проверке, обосновывать его при помощи

личного опыта. Если, например, мне известен

закон Архимеда, то мне совсем не обязательно

искать ванну с водой, чтобы, поместив туда

предмет, выяснить, сколько он потерял в весе.

Закон Архимеда будет достаточным основанием

для подтверждения этого частного случая.

Целью науки является не только добывание

знания, но и его передача. Именно по-этому

недопустимы никакие логические огрехи в

формальном представлении уже добытого знания.

Таким образом - знание должно быть логически

контролируемым. Именно это оптимально для его

сохранения, передачи и развития. И именно

поэтому научное знание, как совокупность уже

доказанных логических предложений, может

служить основанием для последующих

доказательных рассуждений.

Закон достаточного основания фактически

сводится к следующему требованию: "всякое

суждение, прежде чем быть принятым за истину,

должно быть обосновано". Таким образом из этого

закона вытекает, что при правильном рассуждении

ничто не должно приниматься просто так, на веру.

В каждом случае каждого утверждения следует

указывать основания, в силу которых оно

считается истинным. Как видим - закон

достаточного основания изначально выступает,

как методологический принцип, обеспечивающий

способность

мышления поставлять основания к

последующим рассуждениям. Ведь все, что уже

корректно доказано, можно положить в основу

последующим доказательствам.

Вывод: достаточным основанием какой либо

мысли может быть любая другая, уже проверенная

и признанная истинной мысль, из которой

вытекает истинность рассматриваемой мысли.

Результат применения: закон обеспечивает

обоснованность мышления. Во всех случаях, когда

мы утверждаем что-либо, мы обязаны доказать

свою правоту, т.е. привести достаточные

основания, подтверждающие истинность наших

мыслей.

38. Формы развития научного знания: факты

науки, проблема, гипотеза, док-тво, теория.

Осваивая действительность самыми

разнообразными методами, научное знание

проходит разные этапы. Каждому из них

соответствует определенная форма развития

знаний. Основными из этих форм являются: факт,

теория, проблема (задача), гипотеза,

доказательство.

Научный факт – факт, описанный в научных

терминах и поддающийся проверке.

Проблема – форма знания, рожденная из

потребности объяснить факт. Это своего рода

знание о незнании, вопрос требующий ответа.

Правильно поставить проблему – значит поставить

вопросы и определить средства их решения.

Гипотеза – форма знания, содержащая

предположение, сформулированное на основе на

ряде факторов, истинное значение которого не

определено и нуждается в доказательстве.

Проверенная и доказанная гипотеза переходит в

разряд достоверных истин и становится научной

истиной.

Теория – высшая форма научного познания,

дающая целостное отображение

закономерных и существенных связей

определенной области действительности.

Доказательство — рассуждение,

устанавливающее истинность какого-либо

утверждения путем приведения других

39. Понятие и виды гипотезы. Судебно-

следственная версия как разновидность частной

гипотезы.

Гипотеза — это закономерная форма развития

знаний, представляющая собою обоснованное

предположение, выдвигаемое с целью выяснения

свойств и причин исследуемых явлений.

Характерные черты гипотезы:1) Гипотеза — это

всеобщая и необходимая для любого познавательного

процесса форма развития знаний. 2) Построение

гипотезы всегда сопровождается выдвижением

предположения о природе исследуемых явлений,

которое является логической сердцевиной гипотезы и

формулируется в виде отдельного суждения или

системы взаимосвязанных суждений. 3) Возникающее

при построении гипотезы предположение рож¬дается в

результате анализа фактического материала, на базе

обобщения многочисленных наблюдений.

Важную роль в возникновении плодотворной

гипотезы играет интуиция, творческие способности и

фантазия исследователя.

Виды гипотез. В процессе развития знаний гипотезы

различаются по своим познавательным функциям и по

объекту исследования.

1. По функциям в познавательном процессе различают

гипотезы: (1) описательные и (2) объяснительные.1)

Описательная гипотеза — это предположение о

присущих исследуемому объекту свойствах. Оно

обычно отвечает на вопрос: «Что представляет собой

данный предмет или какими свойствами он обладает»,

Описательные гипотезы могут выдвигаться с целью

выявления состава или структуры объекта,

раскрытия механизма или процедурных

особенностей его деятельности, определения

функциональных характеристик объекта.2)

Объяснительная гипотеза — это предположение о

причинах возникновения объекта исследований.

Отвечает на вопрос: «Почему произошло данное

событие и каковы причины появления данного

предмета» (г. о Тунгусском метеорите, ледниковом

периоде)

2. По объекту исследования различают гипотезы:

общие и частные.1) Oбщей гипотезой называют

обоснованное предположение о закономерных связях и

об эмпирических регулярностях. 2) Частная гипотеза

— это обоснованное предположение о происхождении

и свойствах единичных фактов, конкретных событий и

явлений (гипотеза о личности преступника). Если

единичное обстоятельство послужило причиной

возникновения других фактов и если оно недоступно

непосредственному восприятию, то познание его

принимает форму гипотезы о существовании или о

свойствах этого обстоятельства.

3. По степени достоверности различают научные и

рабочие гипотезы. Научной называется гипотеза,

объясняющая закономерности развития явлений

природы, общества и мышления. Чтобы быть научной,

гипотеза должна отвечать следующим требованиям:

а)быть единственным аналогом данного процесса

явления, б)давать объяснение как можно большему

числу связанных с этим явлением обстоятельств, в)

быть способной предсказывать новые явления, не

входящие в число тех, на основе которых она

строилась. Рабочая гипотеза — это выдвигаемое на

первых этапах исследования предположение, которое

допущением, позволяющим сгруппировать

результаты наблюдений и дать им первоначальное

объяснение. В зависимости от способа и степени

доказательности гипотез, существуют различные

варианты теоретического знания: учение, концепция,

теория, научная теория.

2. Судебно-следственная версия как

разновидность частной гипотезы. В историческом,

социологическом или политологическом исследования,

а также в судебно-следственной практике при

объяснении отдельных фактов или совокупности

обстоятельств часто выдвигают ряд гипотез, по-

разному объясняющих эти факты. Такие гипотезы

называют версиями (от латинского versio — «оборот»,

versare — «видоизменять»). Версия в судопроизводстве

— одна из возможных гипотез, объясняющих

происхождение или свойства отдельных юридически

значимых обстоятельств или преступления в целом.

При расследовании преступлений и судебном

разбирательстве строят различные по содержанию и

охвату обстоятельств версии. Среди них различают

общие версии и версии частные.

(1) Общая версия — это предположение, объясняющее

все преступления в целом как единую систему

конкретных обстоятельств. Она отвечает не на один, а

на множество взаимосвязанных вопросов, выясняя всю

совокупность юридически значимых обстоятельств

дела. Важнейшими среди этих вопросов будут

следующие: какое преступление совершено? кто его

совершил? где, когда, при каких обстоятельствах и

каким способом оно совершено? каковы цели, мотивы

преступления, вина преступника?

Неизвестной реальной причиной, по поводу которой

создается версия, выступает не принцип развития или

объективная закономерность, а конкретная

совокупность фактических обстоятельств, из которых

складывается единичное преступление. Освещая все

подлежащие выяснению в суде вопросы, такая версия

носит черты общего суммирующего предположения,

объясняющего все преступление в целом.

(2) Частная версия — это предположение,

объясняющее отдельные обстоятельства

рассматриваемого преступления. Будучи неизвестным

или малоизвестным, каждое из обстоятельств может

быть предметом самостоятельного исследования, по

поводу каждого из них также создаются версии,

объясняющие особенности и происхождение этих

обстоятельств.

Примерами частных версий могут быть следующие

предположения: о местонахождении похищенных

вещей или о местонахождении преступника; о

соучастниках деяния; о способе проникновения

преступника к месту совершения деяния; о мотивах

совершения преступления и многие другие.

Частные и общие версии тесно взаимосвязаны друг

с другом в процессе расследования. Знания,

полученные с помощью частных версий, служат

основной для построения, конкретизации и уточнения

общей версии, объясняющей преступное деяние в

целом. В свою очередь, общая версия дает

возможность наметить основные направления для

выдвижения частных версий по поводу еще не

выявленных обстоятельств дела.

40. Логико-методологические требования к

построению гипотезы и ее особенности в

профессиональном исследовании.

Гипотеза- это закономерная форма развития

знаний, представляющая собою обоснованное

предположение, выдвигаемое с целью выяснения

свойств и причин исследуемых явлений. Версия -

одна из гипотез.

Построение версии в судебном исследовании,

как и любой гипотезы, складывается из трех

последовательных этапов

1. Анализ фактов. Цель анализа — выделить

среди множества фактических обстоятельств

такие, которые прямо или косвенно, явно или

неявно, близко или отдаленно связаны с

преступным событием. Исходный фактический

материал обнаруживают в процессе производства

осмотров и обысков, при ознакомлении с

документами, при допросах свидетелей и

обвиняемых. В процессе анализа важно выявить у

различных фактических обстоятельств нечто

общее, а именно наличие их связи с

преступлением. Обобщение на этом уровне решает

важную задачу относимости доказательственного

материала: из множества исследованных фактов

отбирают лишь такие, которые дают основание

для предположения об их связи с преступлением.

2. Синтез фактов Новый шаг в логической

обработке фактов — это синтез, то есть мысленное

объединение аналитически выделенных фактов в

единство, при отвлечении от случайных

обстоятельств. Расследование преступлений

требует развитого аналитико-синтезирующего

мышления, умения правильно связывать факты,

выявлять среди них особенное, специфическое.

Синтез фактических данных в единую систему

является основной предпосылкой построения

гипотезы, или версии — рождения обоснованного

предположения о событии преступления.

3. Выдвижение предположения Логический

механизм выдвижения предположения на основе

анализа и синтеза сводится к следующему.

Исходный фактический материал анализируют в

свете научных и практических обобщений,

отделяют существенное от несущественного и

синтезируют относящиеся к делу факты в

непротиворечивое множество .

Условия состоятельности гипотезы. (1) Гипотеза

должна быть непротиворечивой. (2) Гипотеза

должна быть принципиально проверяемой,(3)

Гипотеза считается состоятельной, если она

эмпирически и теоретически обоснована. (4)

Познавательная, или эвристическая ценность

гипотезы определяется ее информативностью,

которая выражается в предсказательной и

объяснительной силе гипотезы —

в ее способности предсказать, — где и как

отыскать новые, еще не известные факты и дать

им рациональное объяснение.

Проверка гипотезы . Гипотеза, или версия,

проверяется в два этапа: первый из них

дедуктивное выведение вытекающих из гипотезы

следствий, второй — сопоставление следствий с

фактами.

Вероятностный подход к вопросу о

подтверждении гипотезы путем подтверждения

вытекающих из нее следствий имеет важное

эвристическое значение для судебно-следственной

практики, поскольку показывает принципиальную

тенденцию повышения вероятностного значения

гипотез. Вместе с тем, сколь бы вероятной ни была

судебная, следственная или оперативная версия,

она не может служить основой для принятия

правосудного решения по обвинению конкретных

лиц в совершении тех или других преступлений.

Правосудное решение суда всегда должно быть

основано на достоверном знании обстоятельств

рассматриваемого дела. Это значит, что каждая

гипотеза в судебном исследовании должна быть

доказана и тем самым должна превратиться в

несомненное знание, содержащее объективную

истину !

41. Способы доказательства гипотезы.

Значение гипотезы в деятельности

современного специалиста.

Основными способами доказательства гипотез

являются следующие: дедуктивное обоснование

выраженного в гипотезе предположения;

непосредственное обнаружение предположенных

в гипотезе предметов; логическое доказательство

гипотезы. Дедуктивное выведение предположений

уже рассматривалось и сейчас остановимся на

последних двух.

Непосредственное обнаружение искомых

предметов. Частные гипотезы в науке и версии в

судебном исследовании нередко ставят своей

задачей выявление факта существования в

определенное время и в определенном месте

конкретных предметов и явлений либо отвечают

на вопрос о свойствах и качествах таких

предметов. Наиболее убедительным способом

превращения такого предположения в достоверное

знание является непосредственное обнаружение в

предположенное время или в предположенном

месте искомых предметов либо непосредственное

восприятие предположенных свойств.

Например, при расследовании уголовных дел о

хищениях, а также о разбое, бандитизме,

мошенничестве и т.п. важной задачей судебно-

следственных органов является обнаружение

приобретенных или накопленных преступным

путем вещей, ценностей и денежных сумм. Эти

ценности и вещи, как правило, прячутся или

реализуются преступниками. В связи с этим и

возникают частные версии о местонахождении

таких вещей и ценностей.

Версии, доказываемые непосредственным

обнаружением предположенной причины, всегда

являются частными версиями. С их помощью, как

правило, устанавливаются лишь отдельные

фактические обстоятельства дела, частные

стороны события преступления.

Логическое доказывание версий. Версии,

объясняющие существенные обстоятельства

расследуемых дел, превращаются в достоверное

знание путем логического обоснования. Оно про-

текает опосредованным путем, ибо познаются

события, имевшие место в прошлом, или явления,

существующие и в настоящее время, но

недоступные непосредственному восприятию. Так

доказываются, например, версии о способе

совершения преступления, о виновности, о

мотивах совершения преступления, объективных

обстоятельствах, при которых было совершено

деяние, и т.п.

Логическое доказывание гипотезы в

зависимости от способа обоснования может

протекать в форме косвенного или прямого

доказывания.

Косвенное доказывание протекает путем

опровержения и исключения всех ложных версий,

единственного оставшегося предположения.

Заключение в этом выводе может

расцениваться как достоверное, если, во-первых,

построен исчерпывающий ряд версий,

объясняющих исследуемое событие, и, во-вторых,

в процессе проверки версий опровергнуты все

ложные предположения. Версия, указывающая на

оставшуюся причину, в этом случае будет

единственной, а выраженное в ней знание будет

выступать уже не как проблематичное, а как

достоверное.

Этот способ доказывания, протекающий по

методу исключения, часто используется в судебно-

следственной практике при доказывании как

общих, так и частных версий.

Косвенное доказывание должно сочетаться с

прямым обоснованием оставшегося

предположения.

Прямое доказывание гипотезы протекает путем

выведения из предположения разнообразных, но

вытекающих только из данной гипотезы следствий

и подтверждения их вновь обнаруженными

фактами.

При отсутствии косвенного доказывания

простое совпадение фактов с теми следствиями,

которые выведены из версии, нельзя расценивать

как достаточное основание истинности версии,

ибо совпадающие факты могли быть вызваны и

другой причиной.

При соблюдении указанных условий в

судебном исследовании приходят к такому знанию

об обстоятельствах преступления и его

участниках, которое является достоверным,

единственно возможным и не вызывает сомнений

в своей истинности.

42. Понятие доказательства. Логическое

доказательство и судебное доказательство.

Доказательство - это совокупность логических

приемов обоснования истинности тезиса. Док-во

связано с убеждением, но не тождественно ему :

док-ва должны основываться на на данных науки,

убеждения же могут быть основаны, например, на

религиозной вере, на предрассудках, поэтому

убедить, это еще не значит доказать.

Общая характеристика доказательств

Аргументация в различных областях науки и

практики не всегда дает однозначные по

логической ценности результаты. Так, при

построении версий в судебном исследовании

недостаточность исходного фактического

материала позволяет получать лишь

правдоподобные заключения. Такие же результаты

получает исследователь, когда использует в

рассуждении умозаключения по аналогии или

умозаключения неполной индукции.

В других случаях, когда исходный материал

установлен с достоверностью и достаточен для

применения в процессе обоснования

демонстративных рассуждений, аргументативный

процесс обеспечивает получение достоверного,

объективно истинного знания. Такого рода

аргументация приобретает характер строгого

рассуждения и именуется доказательством.

Доказательство — это логическая операция

обоснования истинности какого-либо суждения с

помощью других истинных и связанных с ним

суждений.

Таким образом, доказательство — это одна из

разновидностей процесса аргументации, а именно

аргументация, устанавливающая истинность

суждения на основе других истинных суждений.

Новые идеи в науке не принимаются на веру,

какой бы авторитетной ни была личность ученого

и его уверенность в правильности своих идей. Для

этого надо убедить других в правильности новых

идей не силой авторитета, психологическим

влиянием или красноречием, а прежде всего силой

логики — последовательным и строгим

доказательством исходной идеи. Доказательное

рассуждение — характерная черта научного стиля

мышления.

48. Логические парадоксы, их роль в

развитии профессиональных знаний.

Что такое логический парадокс

Никакого исчерпывающего перечня логических

парадоксов не существует, да он и невозможен.

Рассмотренные парадоксы — это только часть из

всех обнаруженных к настоящему времени.

Вполне вероятно, что в будущем откроют и

многие другие парадоксы, и даже совершенно

новые их типы. Само понятие парадокса не

является настолько определенным, чтобы удалось

составить список хотя бы уже известных

парадоксов.

«Теоретико-множественные парадоксы

являются очень серьезной проблемой, не для

математики, однако, а скорее для логики и теории

познания», — пишет австрийский математик и

логик К.Гедель. «Логика непротиворечива. Не

существует никаких логических парадоксов», —

утверждает математик Д.Бочвар. Такого рода

расхождения иногда существенны, иногда

словесны. Дело во многом в том, что именно

понимается под логическим парадоксом.

Парадокс - это рассуждение, доказывающее как

истинность , так и ложность одного и того же

суждения.

Парадокс “куча” - разница между кучей и

некучей не в 1-й пиздчинке. Пусть у нас есть куча

(напр. Песка). Начинаем от нее брать каждый раз

по 1-й пиздчинке, и куча остаеттся кучей. Итак -

100 пиздчинок - куча, 99 - куча, 10 - куча, 9 - куча

и 1 - тоже куча. Суть - постепенные

количественные изменения не приводят к

изменениям качественным.

Парадокс - генерал и брадобрей. Каждый солдат

может бриться сам или бриться у другого солдата.

Генерал издал указ, по которому назначался один

солдат в брадобреи и он мог брить только тех

солдат, кто не бреется сам. Как же тогда бриться

этому солдату-брадобрею?

43. Логическая структура доказательства.

Способы доказательства.

Структура доказательства - тезис - это суждение,

истинность которого надо доказать. Форма

доказательства (демонстрация) - это способ логической

связи между тезисом и аргументами. Аргументы - это

те истинные суждения, которыми пользуются при

доказательстве тезиса.

Аргументы бывают : 1. Удостоверенные единичные

факты (фактический материал - подписи лица на

документе, статистические данные, свидетельские

показания и т.п.). 2. Определения (определения

понятий, например научные). 3. Аксиомы и постулаты

(это суждения, которые принимаются в качестве

аргументов и без доказательств). 4. Ранее доказанные

законы науки и теоремы - (напр. Юридические законы

являются аргументами в ходе судебного

доказательства).

Опровержение - это логическая операция

установления ложности или необоснованности ранее

выдвинутого тезиса. Опровержение должно показать,

что : 1. Неправильно построено само доказательство.

2. Выдвинутый тезис ложен или недоказан. Есть 3 вида

опровержения - Опровержение тезиса, критика

аргументов, выявление несостоятельности

демонстрации.

ВИДЫ ДОКАЗАТЕЛЬСТВА - ПРЯМЫЕ И

КОСВЕННЫЕ

Доказательства по форме делятся на прямые и

косвенные.

Прямое идет от расмотрения аргументов к

доказательству тезиса, т.е. истинность тезиса

непосредственно обосновывается аргументами. Из

“Все углеводы горючи. Сахар - углевод,

следовательно сахар - горюч” - это прямое

доказательство в форме КС.

Косвенное - это доказательство, в котором

истинность выдвинутого тезиса обосновывается путем

ложности антитезиса. “Преступление могли совершить

либо А, либо Б, либо В. Доказано, что преступления не

совершали А и Б. След-но преступление совершил В.”.

Структура доказательства

Аргументация включает три взаимосвязанных

элемента: тезис, аргументы, демонстрацию..

1. Тезис — это выдвинутое пропонентом суждение,

которое он обосновывает в процессе аргументации.

Тезис является главным структурным элементом

аргументации и отвечает на вопрос: что обосновывают

В качестве тезиса могут выступать теоретические

положения науки, которые складываются из одного,

нескольких или целой системы взаимосвязанных

суждений.

Аргументы, или доводы, — это исходные

теоретические или фактические положения, с помощью

которых обосновывают тезис. Они выполняют роль

основания, или логического фундамента аргументации,

и отвечают на вопрос: чем, с помощью чего ведется

обоснование тезиса"?

Доказательство и опровержение.

Критика тезиса — весьма эффективная по

разрушительной силе операция, цель которой —

показать несостоятельность тезиса. Такая критика

называется опровержением тезиса. Тезис расценивают

как заведомо ложный, если пропонент заранее знал об

этом, но тем не менее отстаивал его, создавая

видимость аргументации.

Ошибочным тезис будет в том случае, если

пропонент заблуждался относительно действительного

логического статуса своего утверждения.

Рассмотрим прямое опровержение тезиса, которое

строится в форме рассуждения, получившего название

«сведение к абсурду».

Аргументация в этом случае протекает в следующем

виде. Вначале делают апагогический шаг, т.е. условно

допускают истинность выдвинутого пропонентом

положения и выводят логически вытекающие из него

следствия. Рассуждают при этом примерно так:

допустим, что пропонент прав и его тезис является

истинным, но в этом случае из него вытекают такие-то

и такие-то следствия.

Если при сопоставлении следствий с фактами

окажется, что они противоречат объективным данным,

то тем самым их признают несостоятельными. На этой

основе заключают о несостоятельности самого тезиса,

рассуждая по принципу: ложные следствия всегда

свидетельствуют о ложности их основания

В процессе аргументации прямое опровержение

выполняет разрушительную, или деструктивную,

функцию. С его помощью демонстрируют

несостоятельность тезиса пропонента, не выдвигая

никакой идеи взамен. Несмотря на чисто критическую

функцию, опровержение «сведением к абсурду» часто

оказывается полезным. В науке оно служит средством

проверки на надежность различного рода гипотез и

теорий. В процессе судебного разбирательства с его

помощью можно показать несостоятельность

выдвинутого обвинителем тезиса.

(2). Критика аргументов. Поскольку аргументация

— это обоснование тезиса с помощью ранее

установленных положений, то следует пользоваться

доводами, истинность которых не вызывает сомнений.

Если оппоненту удается показать сомнительность или

ложность аргументов, то существенно ослабляется

позиция пропонента, ибо такая критика показывает

необоснованность его тезиса.

Критика аргументов может выражаться в том, что

оппонент указывает на неточное изложение фактов,

двусмысленность процедуры обобщения

статистических данных, выражает сомнения в

авторитетности эксперта, на заключение которого

ссылается пропонент, и т.д. С такого рода

критическими замечаниями пропонент не может не

считаться. Он должен либо подтвердить свои

аргументы, либо отказаться от них.

46. Правила и ошибки доказательств.

Правила и ошибки, относящиеся к тезису

Правила.

1. Тезис должен быть логически определенным,

ясным и точным. Иногда люди в своем выступлении,

лекции не могут четко, ясно, однозначно

сформулировать тезис.

2. Тезис должен оставаться тождественным, т.е.

одним и тем же на протяжении всего доказательства

или опровержения.

Ошибки.

1. “Подмена тезиса”. Согласно правилам

доказательного рассуждения, тезис должен быть ясно

сформулирован и оставаться одним и тем же на

протяжении всего доказательства или опровержения.

При нарушении его возникает ошибка называемая

“подмена тезиса”. Суть ее в том, что один тезис

умышленно или неумышленно подменяют другим и

этот новый тезис начинают доказывать или

опровергать. К примеру, надо показать, что на осине не

могут расти яблоки; вместо этого доказывается, что

они растут обычно на яблоне и не встречаются ни на

груше, ни на вишне.

2. “Довод к человеку”. Ошибка состоит в подмене

доказательства самого тезиса ссылками на личные

качества того, кто выдвинул этот тезис. Например,

вместо того чтобы доказывать ценность и новизну

диссертационной работы, говорят, что диссертант

заслуженный человек, что он много потрудился над

диссертацией и т.д. В научных работах иногда вместо

конкретного анализа материала, изучения современных

научных данных и результатов практики в

подтверждение приводят цитаты из высказываний

крупных ученых, видных деятелей и этим

ограничиваются, полагая, что одной ссылки на

авторитет достаточно. Разновидностью “довода к

человеку” является ошибка, называемая “довод к

публике”, состоящая в попытке повлиять на чувства

людей, чтобы те поверили в истинность выдвинутого

тезиса, хотя его и нельзя доказать.

3. “Переход в другой род”. Имеются две

разновидности этой ошибки: а) “кто слишком много

доказывает, тот ничего не доказывает”; б) “кто

слишком мало доказывает, тот ничего не доказывает”.

В первом случае ошибка возникает тогда, когда вместо

одного истинного тезиса пытаются доказать другой,

более сильный тезис, и при этом второй тезис может

оказаться ложным. Если из а следует б, но из б не

следует а, то тезис а является более сильным, чем тезис

б. Например, если вместо того чтобы доказывать, что

этот человек не начинал первым драку, начнут

доказывать, что он не участвовал в драке, то ничего не

смогут доказать, если этот человек действительно

дрался и кто-нибудь это видел. Ошибка “кто слишком

мало доказывает, тот ничего не доказывает” возникает

тогда, когда вместо тезиса а мы докажем более слабый

тезис б. Например, если, пытаясь доказать, что это

животное зебра, мы доказываем, что оно полосатое, то

ничего не докажем, так как тигр тоже полосатое

животное.

Правила и ошибки, относящиеся к аргументам

Правила: Аргументы, приводимые для

доказательства тезиса, должны быть истинными.

Аргументы должны быть достаточным основанием для

доказательства тезиса.

Аргументы должны быть суждениями, истинность

которых доказана самостоятельно, независимо от

тезиса.

Ошибки. 1. Ложность основания (“Основное

заблуждение”). В качестве аргументов берутся не

истинные, а ложные суждения, которые выдают или

пытаются выдать за истинные. Ошибка может быть

непреднамеренной и преднамеренной (софизмом),

совершенной с целью запутать, ввести в заблуждение

других людей Употребление ложных, недоказанных

или непроверенных аргументов нередко

сопровождается оборотами: “всем известно”, “давно

установлено”, “совершенно очевидно”, “никто не

станет отрицать” и т.п. Слушателю как бы оставляется

одно: упрекать себя за незнание того, что давно и всем

известно.

2. “Предвосхищение оснований”. Эта ошибка

совершается тогда, когда тезис опирается на

недоказанные аргументы, последние же не доказывают

тезис, а только предвосхищают его.

3. “Порочный круг”. Ошибка состоит в том, что

тезис обосновывается аргументами, а аргументы

обосновываются этим же тезисом. Эта разновидность

ошибки “применение недоказанного аргумента”.

Правила и ошибки, относящиеся к демонстрации

Правила. Тезис должен быть заключением,

логически следующим из аргументов по общим

правилам умозаключений или полученным в

соответствии с правилами косвенного доказательства.

Ошибки.

1. Мнимое следование. Если тезис не следует из

приводимых в его подтверждение аргументов,

то возникает ошибка, называемая “не следует”.

Иногда вместо правильного доказательства аргументы

соединяют с тезисом посредством слов:

“следовательно”, “итак”, “таким образом”, “в итоге

имеем” и т.п., полагая, что установлена логическая

связь между аргументами и тезисом. Эту логическую

ошибку часто неосознанно допускают люди, не

знакомые с правилами логики, полагающиеся на свой

здравый смысл и интуицию. В результате возникает

словесная видимость доказательства.

2. От сказанного с условием к сказанному

безусловно. Аргумент, истинный только с учетом

определенного времени, отношения, меры, нельзя

приводить в качестве безусловного, верного во всех

случаях. Так, если кофе полезен в небольших дозах

(например, для поднятия артериального давления), то в

больших дозах он вреден. Аналогично мышьяк ядовит,

но в небольших дозах его добавляют в некоторые

лекарства. Педагогика требует индивидуального

подхода к учащимся; этика определяет нормы

поведения людей, и в различных условиях они могут

несколько варьироваться.